考虑修形的双列圆锥滚子轴承热特性研究*

王一铭,王恒迪,崔永存,李 畅,邓四二*

(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.山东朝阳轴承有限公司, 山东 德州 252600)

0 引 言

双列圆锥滚子轴承广泛应用于重型卡车的车桥中,其中位于轮毂单元的轴承起到了支撑整车重量的作用,轴承承载较大。双列圆锥滚子轴承滚动体与滚道接触形式是线接触,通过修形可以有效地改善滚子与滚道接触区的温度分布,避免出现局部高温情况,进而影响轴承寿命。多年来,修形对重型卡车车桥用双列圆锥滚子轴承的影响得到了许多学者的关注。

ANDREASON S等人[1]基于向量法,分析了圆锥滚子轴承各元件的受力及位移。GUPTA P K等人[2,3]构建了圆锥滚子轴承的动力学分析软件ADORE,采用该建模方法对润滑条件下的轴承特性进行了分析,分析结果对于研究轴承的动力学特性具有重要意义。邓四二等人[4]1899-1902构建了基于经典Hertz线接触理论的双列圆锥滚子轴承非线性动力学模型和摩擦功耗模型,并借此对轴承摩擦功耗特性进行了研究。LUNDBERG G等人[5]提出了一种滚子的对数型母线,该对数型母线是目前被认为最好的修形母线。王爱林等人[6]构建了考虑滚子对数修形的滚子和滚道间接触模型,研究结果表明,经过对数修形的圆锥滚子能够有效地改善轴承端部的应力集中现象,载荷与滚子修形量间具有匹配性。王超等人[7,8]基于赫兹接触理论和滚子修形母线理论,建立了圆锥滚子轴承滚子与滚道接触区域应力、载荷的数学模型,借此分析了采用不同修形的滚子在其素线方向的应力与载荷分布。

一些学者同时对双列圆锥滚子轴承的热分析做了研究。

WANG Ai-lin、阚锦彪等人[9,10]分别建立了集单个圆锥滚子的局部有限元热分析模型、采煤机行星机构用双列圆锥滚子轴承摩擦功耗,以及基于ANSYS软件的轴承稳态热分析模型;虽然这些模型均对轴承做出了简化,但其忽略了多个元件间的相互作用。邢磊等人[11]基于Palmgren经验公式,建立了双列圆锥滚子摩擦功耗模型,并基于有限元、热网络法,对轴承温度特性进行了研究。AI Si-yuan等人[12]建立了集双列圆锥滚子轴承静态模型和基于热网络法的热分析模型,模型分析结果表明,温度最大值位于滚子大端与挡边接触处。耿自林等人[13]构建了双列圆锥滚子轴承动力学分析模型和轴承各元件接触处的摩擦功耗模型,并且利用热网络法研究了轴承的热特性。LI Jun-ning等人[14]提出了一种圆锥滚子轴承动态产热计算方法,分析了圆锥滚子的温度分布。韩庆利等人[15]基于经验公式,建立了双列圆锥滚子摩擦功耗模型,并使用ANSYS软件分析了轴承的热特性。

很多学者对圆锥滚子的修形进行了分析,但大多数的研究都集中于滚子修形对轴承接触区域应力分布和载荷分布等方面的影响,很少有研究人员对基于滚子和滚道修形的双列圆锥滚子轴承接触区热特性进行系统性的研究。

因为以上论述,笔者基于滚动轴承动力学和热传递理论,建立考虑滚子与滚道修形的重卡车桥用双列圆锥滚子轴承动力学模型、摩擦功耗模型和有限元温度场模型;并基于滚子、滚道修形参数,对双列圆锥滚子轴承温度场影响进行研究;最后利用某铁路轴承试验机对模型进行实验和仿真分析。

1 双列圆锥滚子轴承动力学模型

1.1 轴承动力学坐标系

笔者对某型号重卡车桥用双列圆锥滚子轴承进行研究,其外圈旋转,内圈固定,轴承结构及坐标系如图1所示。

图1 轴承结构及坐标系

为描述各元件运动及受力,笔者建立了整体及局部坐标系。

惯性坐标系:{O;X,Y,Z},其位置不变,是局部坐标系的参考;外圈坐标系:{ol(r)o;xl(r)o,yl(r)o,zl(r)o},l、r为左、右列,下同;保持架坐标系:{ol(r)c;xl(r)c,yl(r)c,zl(r)c};滚子坐标系:{ol(r)gj;xl(r)gj,yl(r)gj,zl(r)gj},j为第j个滚子,下同;兜孔坐标系:{ol(r)pj;xl(r)pj,yl(r)pj,zl(r)pj}。局部坐标系随其零件一起运动。

1.2 滚子与滚道修形表征

重卡行驶过程中,其车桥用双列圆锥滚子轴承会承受较大的径向、轴向载荷和力矩。

笔者将滚子切N片,切片的宽度为Ls/N,其中,Ls为沿滚子轴向的接触长度。

滚子与滚道的对数修形表征如下:

1)滚子:

(1)

2)滚道:

yl(r)i(e)jk=

(2)

式中:a,ai(e)为滚子、套圈的修形系数;νr和Er为圆锥滚子泊松比、弹性模量;νi(e)和Ei(e)为套圈泊松比、弹性模量;Qmax为轴承受最大运行载荷时滚子与滚道的最大接触载荷;xl(r)jk为切片中心在xl(r)gj轴的坐标;y,yi(e)为滚子、套圈的修形偏移量;Li(e)为套圈在xl(r)gj轴方向的有效接触长度。

1.3 轴承动力学微分方程组

1.3.1 圆锥滚子微分方程组

轴承在工作时圆锥滚子的受力如图2所示。

图2 滚子与滚道间作用力示意图

Ql(r)i(e)j为滚子、滚道之间的接触力;Qfl(r)j为滚子、内圈挡边之间的接触力;Qcl(r)y(z)j为滚子、兜孔之间作用力在yl(r)pj、zl(r)pj方向的合力;Tl(r)i(e)j为滚子、滚道之间的拖动力;Ffl(r)j为滚子、内圈挡边之间的摩擦力;FOl(r)j为滚子在润滑剂阻碍作用下的阻力;Ml(r)i(e)tj,Ml(r)i(e)qj为滚子、滚道之间的力矩;Mfl(r)j,Mfl(r)yj,Mfl(r)zj为滚子、大挡边之间的力矩;Mcl(r)j为滚子、保持架之间的力矩。

笔者建立圆锥滚子在惯性坐标系的非线性动力学微分方程为[4]1900:

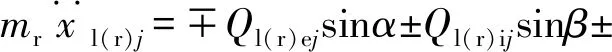
(3)

∓Tl(r)ijsinφj+Qfl(r)jsinθcosφj∓Ffl(r)jsinφj-

Qcl(r)yjcosγcosφj∓Qcl(r)zjsinφj+FOl(r)jsinφj

(4)

cosβsinφj∓Tl(r)ijcosφj-Qfl(r)jsinθsinφj∓Ffl(r)jcosφj+

Qcl(r)yjcosγsinφj∓Qcl(r)zjcosφj+FOl(r)jcosφj

(5)

Tl(r)ij)cosγ∓Mfl(r)jcosγ±Mfl(r)yjsinγ∓Mcl(r)jcosγ

(6)

-Ml(r)itjcosβcosφj-0.5D(Tl(r)ej+Tl(r)ij)sinγcosφj-

Mfl(r)yjcosγcosφj∓Mfl(r)zjsinφj-Mfl(r)jsinγcosφj-

Mcl(r)jsinγcosφj

(7)

+Ml(r)itjcosβsinφj+0.5D(Tl(r)ej+Tl(r)ij)sinγsinφj+

Ml(r)fyjcosγsinφj∓Ml(r)fzjcosφj+Ml(r)fjsinγsinφj+

Mcl(r)jsinγsinφj

(8)

1.3.2 保持架微分方程组

笔者建立保持架在惯性坐标系的非线性动力学微分方程为[4]1901:

(9)

(10)

(11)

(12)

(13)

(14)

1.3.3 外圈微分方程组

笔者建立外圈在惯性坐标系的非线性动力学微分方程为[4]1900:

(15)

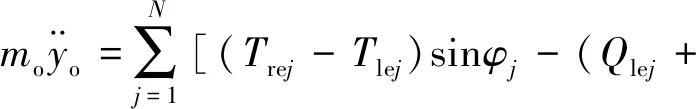
(16)

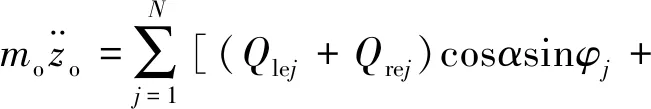
(17)

(18)

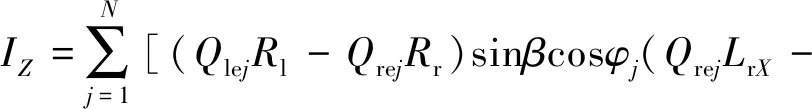
(19)

(20)

(21)

2 双列圆锥滚子轴承热分析模型

2.1 轴承摩擦功耗数学模型

重卡车桥用双列圆锥滚子轴承转动过程中,其产生摩擦功耗主要有五个原因:1)滚子、滚道间弹性滞后;2)滚子、滚道间差动滑动;3)滚子、内圈挡边摩擦;4)滚子、兜孔摩擦;5)滚子、润滑剂摩擦等[16]6-7。

2.1.1 差动滑动引起的摩擦功耗

滚子、内外套圈间因滚道处差动滑动引起的摩擦功耗为:

(22)

式中:Δvl(r)i(e)jk为滚子切片与滚道接触处的相对速度。

2.1.2 弹性滞后引起的摩擦功耗

滚子、内外套圈间因滚道处弹性滞后产生的摩擦功耗为:

(23)

式中:Dpw为节圆直径;ah为弹性滞后损失系数;ql(r)i(e)jk为滚子切片与滚道间接触力;bl(r)i(e)jk为滚子切片与滚道间接触半宽;Rl(r)jk为当量半径[17]22。

2.1.3 挡边处摩擦功耗

滚子、挡边间因摩擦引起的摩擦功耗为:

HDl(r)j=Ffl(r)jΔvfl(r)j

(24)

式中:Δvfl(r)j为滚子、大挡边接触位置的相对速度。

2.1.4 保持架兜孔处摩擦功耗

滚子、保持架接触位置的摩擦功耗为:

HCl(r)j=Fcl(r)j1(2)Δvcl(r)j

(25)

式中:Fcl(r)j1(2)为滚子、兜孔间的摩擦力,1(2)含义为保持架推动或阻碍滚子运动;Δvcl(r)j为滚子、兜孔接触处的相对速度。

2.1.5 润滑脂黏性摩擦功耗

滚子、润滑剂黏性摩擦功耗为:

HOl(r)=0.5DpwFOl(r)j(ωml(r)j-ωe)

(26)

式中:ωml(r)j为滚子公转速度;ωe为外圈转速。

2.1.6 轴承总摩擦功耗

轴承总摩擦功耗为:

(27)

2.2 轴承热传递数学模型

双列圆锥滚子轴承转动时,其产生的热量通过热传导、热对流和热辐射的方式进行交换[16]7。

2.2.1 热传导

基于傅里叶定律的热传导为[17]28:

(28)

2.2.2 热对流

热对流的热量为:

q*=-hf(TS-TB)

(29)

式中:hf为热对流系数;TS为固体温度;TB为流体温度。

2.2.3 热辐射

辐射的热量为:

(30)

(31)

式中:C0为黑体辐射系数;εn为系统黑度;AH为辐射面积;T1(2)为两物体温度;ε1(2)为两物体材料的表面法向黑度。

3 计算结果及分析

此处笔者以某重卡车桥用双列圆锥滚子轴承为例进行分析。该轴承的主要参数如表1所示。

表1 轴承主要参数

动力学和热分析模型的计算流程如图3所示。

图3 模型求解流程图

笔者通过对模型进行求解,能够得到滚子与内、外圈接触区域的温度分布.

滚子与套圈各接触区域的最高温度如图4所示。

图4 滚子与套圈各接触区最高温度图

由图4可知:滚子与大挡边接触区的温度最高,滚子与内、外滚道接触区的温度接近,但内滚道与滚子接触区的温度更高些。

修形主要影响的是滚子与滚道接触区在素线方向的温度分布,且内滚道与滚子接触区域温度较高,故应研究修形参数对内滚道与滚子接触区域温度分布的影响;轴承在仅受径向载荷作用时,承受载荷最大滚子的温度分布相差不大。

3.1 修形参数对轴承热特性的影响

3.1.1 滚子修形参数对轴承热特性的影响

滚子修形参数对右列承受载荷最大滚子与内滚道接触区温度的影响,如图5所示。

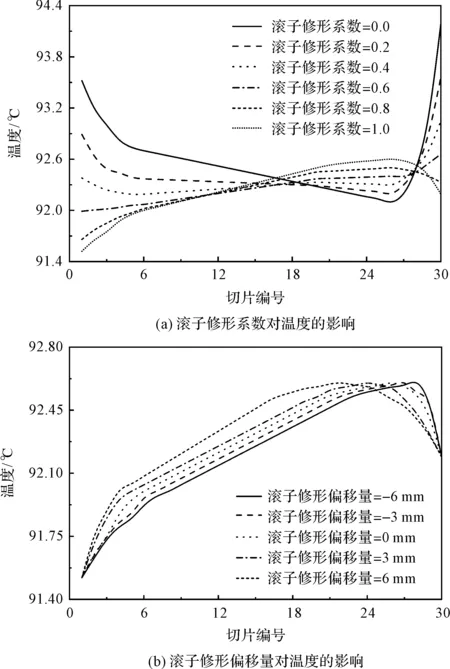
图5 滚子修形对右列受载最大滚子温度的影响

图5(a)为滚子修形偏移量为0 mm时,滚子修形系数对右列受载最大滚子温度的影响。

滚子修形系数增大,滚子与内滚道接触区的两端温度迅速减小并趋于平稳;当接触区两侧的局部高温因修形缓和时,接触区内最高温度则出现在接近滚子大端(切片编号越大越接近滚子大端)一侧,且该温度随滚子修形系数的增大而逐渐增大;滚子修形系数大于0.8时,其能消除应力集中。

图5(b)为滚子修形系数为1时,滚子修形偏移量对右列受载最大滚子温度的影响。

随着滚子修形偏移量由小到大发生变化,接触区内最高温度位置由滚子大端向滚子小端方向移动。这是由于未修形时滚子应力集中,导致滚子与滚道接触区域端部摩擦功耗较大,进而温度也较高。随着滚子修形系数的增大,端部应力集中消失,滚子两端受载逐渐减小,滚子中部受载逐渐增大,以及受滚子与内圈大挡边生热的影响。

因此,应力集中消失后,接近滚子大端一侧的温度较高,并随滚子修形系数增大而增大。

3.1.2 滚道修形参数对轴承热特性的影响

内滚道修形参数对右列承受载荷最大滚子与内滚道接触区温度的影响,如图6所示。

图6 内滚道修形对右列受载最大滚子温度的影响

图6(a)为内滚道修形偏移量为0 mm时,内滚道修形系数对右列受载最大滚子温度的影响。内滚道修形系数增大,滚子与内滚道接触区的温度变化与滚子修形系数增大时的变化基本一致。

图6(b)为内滚道修形系数为1时内,滚道修形偏移量对右列受载最大滚子温度的影响。随着内滚道修形偏移量的增大,接触区的最高温度点也由滚子大端向滚子小端方向移动。这是由于滚子修形与内滚道修形均可作用于滚子与内滚道接触区,因此,两者同向变化对接触区内温度分布影响基本一致。

外滚道修形参数对右列承受载荷最大滚子与外滚道接触区温度的影响,如图7所示。

图7 外滚道修形对右列受载最大滚子温度的影响

图7(a)为外滚道修形偏移量为0 mm时,外滚道修形系数对右列受载最大滚子温度的影响。外滚道修形系数增大,滚子与外滚道接触区的两端温度迅速减小并趋于平稳;当接触区两侧应力集中消失时,接触区内最高温度出现在滚子中部,并随外滚道修形系数的增大而逐渐增大。

图7(b)为外滚道修形系数为1时,外滚道修形偏移量对右列受载最大滚子温度的影响。随着外滚道修形偏移量的增大,接触区的最高温度点也由滚子大端向滚子小端方向移动。这是由于滚子修形系数的增大,会使滚子端部应力集中消失,中部载荷增大且摩擦功耗增大,因此滚子中部温度增大。

3.2 滚子与滚道修形参数匹配性对轴承热特性的影响

3.2.1 滚子与内滚道修形参数匹配性的影响

滚子修形系数取1,修形偏移量取0 mm,内滚道修形系数取1,笔者改变内滚道修形偏移量,对右列承受载荷最大滚子与滚道、挡边接触区温度的影响如图8所示。

图8 内滚道修形参数匹配性对轴承温度的影响

由图8可知:随着内滚道修形偏移量的增大,滚子与外滚道接触区最大温度基本不变,滚子与内滚道接触区最大温度先增大后减小,滚子与挡边接触区最大温度先减小后增大。这是由于随着内滚道修形偏移量的增大,滚子与内滚道在轴向平面内的力矩先减小后反向增大,当滚子受力矩作用时,其会产生倾斜,使滚子与大挡边的摩擦功耗增大。

因此,为减小滚子与大挡边的温度,可以使内滚道偏移量与滚子偏移量接近。

3.2.2 滚子与外滚道修形参数匹配性的影响

滚子修形系数取1,修形偏移量取0 mm,外滚道修形系数取1,笔者改变外滚道修形偏移量,对右列承受载荷最大滚子与滚道、挡边接触区温度的影响如图9所示。

图9 外滚道修形参数匹配性对轴承温度的影响

由图9可知:随着外滚道修形偏移量的增大,滚子与外滚道接触区最大温度先增大后减小,滚子与内滚道接触区最大温度基本不变,滚子与挡边接触区最大温度先减小后增大。外滚道修形偏移量增大,会使滚子与外滚道在轴向平面内由每一切片法向力产生的力矩先减小,后反向增大,进而滚子发生倾斜,使滚子与大挡边的摩擦功耗增大。

因此,为减小滚子与大挡边的温度,可以使外滚道偏移量与滚子偏移量接近。

4 模型试验验证

笔者采用铁路轴承试验机,在不同载荷、转速条件下,对某型号重卡车桥用双列圆锥滚子轴承进行试验测试,以验证轴承热特性分析模型的有效性。

试验轴承安装在主轴上,通过电机和传动带驱动内圈旋转,通过电机转速和传动系统获得主轴转速;试验机在外圈外壁的温度测量点处留有空间,使用温度传感器测量外圈外表面处来获取轴承外圈温度;通过作用于轴承外圈的径向载荷加载系统为轴承施加径向载荷。

试验机如图10所示(试验轴承主要参数见表1)。

图10 铁路轴承试验机

对比试验的仿真分析采用内圈旋转方式;环境温度设置为22 ℃。

轴承内圈转速为385 r/min、轴承径向载荷为35 000 N～55 000 N工况下,试验结果与仿真结果的对比图如图11所示。

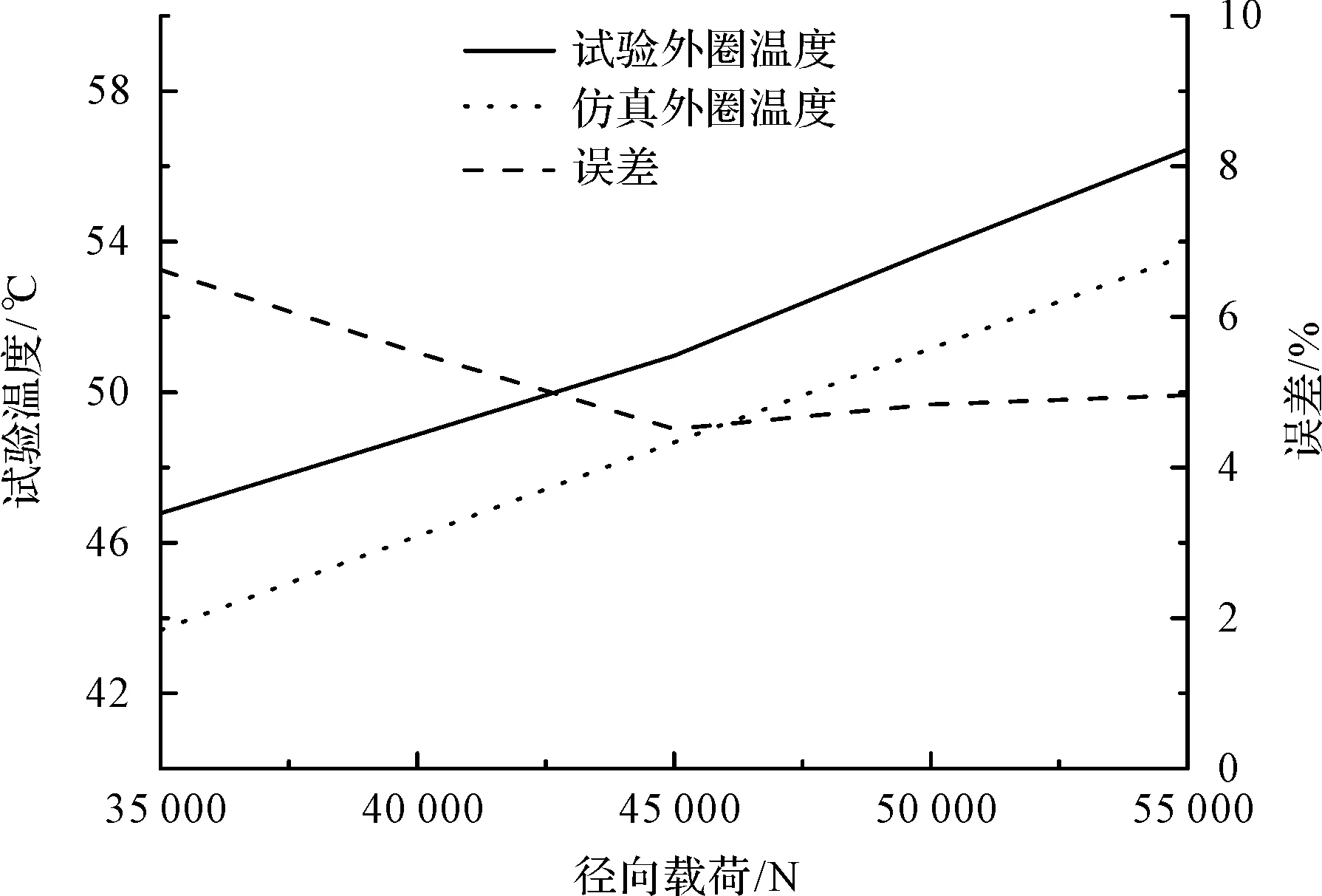
图11 径向载荷对外圈温度的影响

由图11可知:试验和仿真得到的外圈温度变化趋势基本相同,径向载荷增大,外圈温度增大,相对误差<10%。

内圈转速为200 r/min～500 r/min、轴承径向载荷为50 000 N工况下,试验结果和仿真结果的对比图如图12所示。

图12 转速对外圈温度的影响

由图12可知:随着转速的增大,试验和仿真得到的外圈温度均增大,变化趋势基本相同,相对误差<10%。

分析图11和图12可知,笔者建立的轴承热分析数学模型是有效的。

5 结束语

笔者基于滚动轴承动力学理论,构建了基于滚子和滚道修形的重卡车桥用双列圆锥滚子轴承动力学模型、摩擦功耗数学模型和热传递数学模型,分析了不同修形参数对轴承热特性的影响,并得出以下结论:

1)滚子修形参数的变化能够改善滚子与滚道间温度的分布。滚子的修形系数过小,其无法改善滚子与滚道接触区的应力集中;滚子的修形系数过大,其会使滚子与滚道接触区最高温度升高;

2)滚道修形参数的变化能够改善对应滚道与滚子接触区的温度分布,其各参数变化对滚子与滚道接触区温度的影响与滚子修形参数变化的影响基本一致;

3)当滚子与滚道同时进行修形时,由于受滚子倾斜的影响,滚子和滚道的修形偏移量越接近,滚子与大挡边接触区的温度越低。

笔者建立的双列圆锥滚子轴承动力学模型和热分析模型未考虑温度变化对轴承材料和润滑剂性能的影响,而在温度变化下,轴承材料和润滑剂的导热性能也会发生变化,进而对轴承温度产生影响。因此,在后续的研究中,笔者拟进一步考虑材料和润滑剂的热特性。