基于区间二型模糊集的轮系传动方案综合评价*
刘 昊,赵永生,马雅丽,闫立山,董昊天
(大连理工大学 机械工程学院,辽宁 大连 116024)
0 引 言
轮系是动力源和工作装置之间的连接部分,常被用于动力传递、运动变换等。由于其具有结构紧凑、传动平稳、机械效率高等优势,目前轮系已被广泛应用于各种机械设备中。
目前,轮系的传动方案类型多样,如何根据实际使用需求选择最合适的方案,以提高机械设备性能是亟需解决的问题。通常,学者们对于齿轮传动的研究多是聚焦于某一具体方面,例如承载能力、可靠性、振动、误差等,从宏观角度进行综合评价的研究很少。但是,一些学者对其他机械零部件的评价方法进行了研究,可为学术界提供研究思路。
DING Zhou-yang等人[1]将改进的层次分析法和基于连接度的排序偏好技术与理想解方法相结合,为机床导轨的选择提供了可靠的决策支持;但在评价过程中,采用该方法仍存在较强的主观性。对此,GU Ying-kui等人[2]提出了一种基于隐马尔可夫模型的评价方法,以准确评估齿轮箱的断齿和磨损状态,其无需进行指标权重的主观赋予,使评价更为客观。ZHANG Xu-gang等人[3]使用模糊可拓层次分析法,对混凝土泵车动臂油缸进行了评价,提高了其再制造效率。
轮系传动方案的综合评价中存在着众多模糊性因素,对此,可以应用模糊集来处理复杂的模糊性问题。
ZADEH L A[4]首次提出了模糊集的概念,之后在原始模糊集的基础上对其进行了扩展,得到了二型模糊集(type-2 fuzzy sets, T2FSs)[5]。为了克服T2FSs在应用中的缺陷,MENDEL J M等人[6]提出了IT2FSs的概念,引起了业界广泛的关注。LEE L W等人[7]研究了区间二型梯形模糊集(interval type-2 trapezoidal fuzzy sets, IT2TFSs)的运算原理,使IT2FSs的应用从理论变为现实。KILIC M等人[8]应用IT2FSs处理模糊评价指标,灵活选择了投资项目,较好地解决了比较判断的模糊性。ZHOU Lin-tao等人[9]提出了一种基于IT2FSs的多层次、多指标评估模型,并使用去模糊方法处理模糊问题,以此来评估教学表现,选择出教学表现最好的教师;但是复杂的指标体系对于IT2FSs的应用存在指标耦合问题。对此,MENG Fan-yong等人[10]使用IT2FSs构建了交叉熵模型,获得了属性集上的最优模糊测度,对海绵城市建设方案进行了选择,极大地简化了评价流程。
轮系传动方案的综合评价是多准则群决策中的多属性群决策问题。DE A等人[11]使用基于IT2FSs的排序解决了多属性群决策问题,相比于区间一型模糊集的排序,其排序更加准确。VERMA R等人[12]提出了一种基于广义勾股模糊有序加权余弦相似算子的多属性群决策方法,基于该方法实现了对机器人的优选目标,进一步提高了其模糊处理能力。RAO Cong-jun等人[13]提出了使用灰色综合云加权平均处理带有主观和客观不确定语言变量的决策问题,对投资项目进行了选择,为以后解决主客观耦合问题提供借鉴。
作为解决多属性群决策问题的特例,FCE法得到了广泛应用。
CHEN J F等人[14]提出了一种基于FAHP法和FCE法的教学绩效评价方法,并基于该方法对教师的教学表现做出了准确的评价。HU Yan-juan等人[15]提出了基于FCE的定性和定量相结合的方法,解决了评价指标无法公度的问题,对云制造服务进行了选择。ZHANG Wen-jun等人[16]构建了一个基于FAHP联合FCE法的模型,采用该模型评估了长江三角洲的供水网络的水平。
总体来说,近年来各种评价方法被广泛地研究,但鲜有将其有效地应用于轮系传动方案的综合评价上。
为解决传统方案评价缺少合理的方法指导、主观性强等问题,同时针对轮系传动方案评价指标复杂多样,难于将方案评价从定性到定量进行转换的问题,笔者建立IT2FSs-FAHP-FCE的综合评价数学模型,并以某轮系传动方案为例,对基于IT2FSs的轮系传动方案综合评价方法的有效性进行验证。
1 IT2TFSs的表达及运算
经典模糊集被称为一型模糊集,其点值是二维的,隶属函数是简单的。T2FSs是具有三维点值的模糊集,其隶属函数是模糊的。因此,与一型模糊集相比,T2FSs可以更好地解决语言歧义并捕获固有的不确定性,特别是在无法确定模糊集的精确隶属函数时。
由于T2FSs在表达时的局限性仍然存在,IT2FSs目前仍然被广泛使用。作为IT2FSs的一般性表达形式,笔者采用的是IT2TFSs。
1.1 IT2TFSs的数学表达
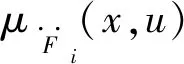
(1)
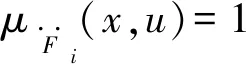
(2)
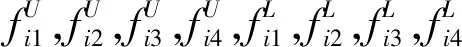
IT2TFSs的数学模型如图1所示。
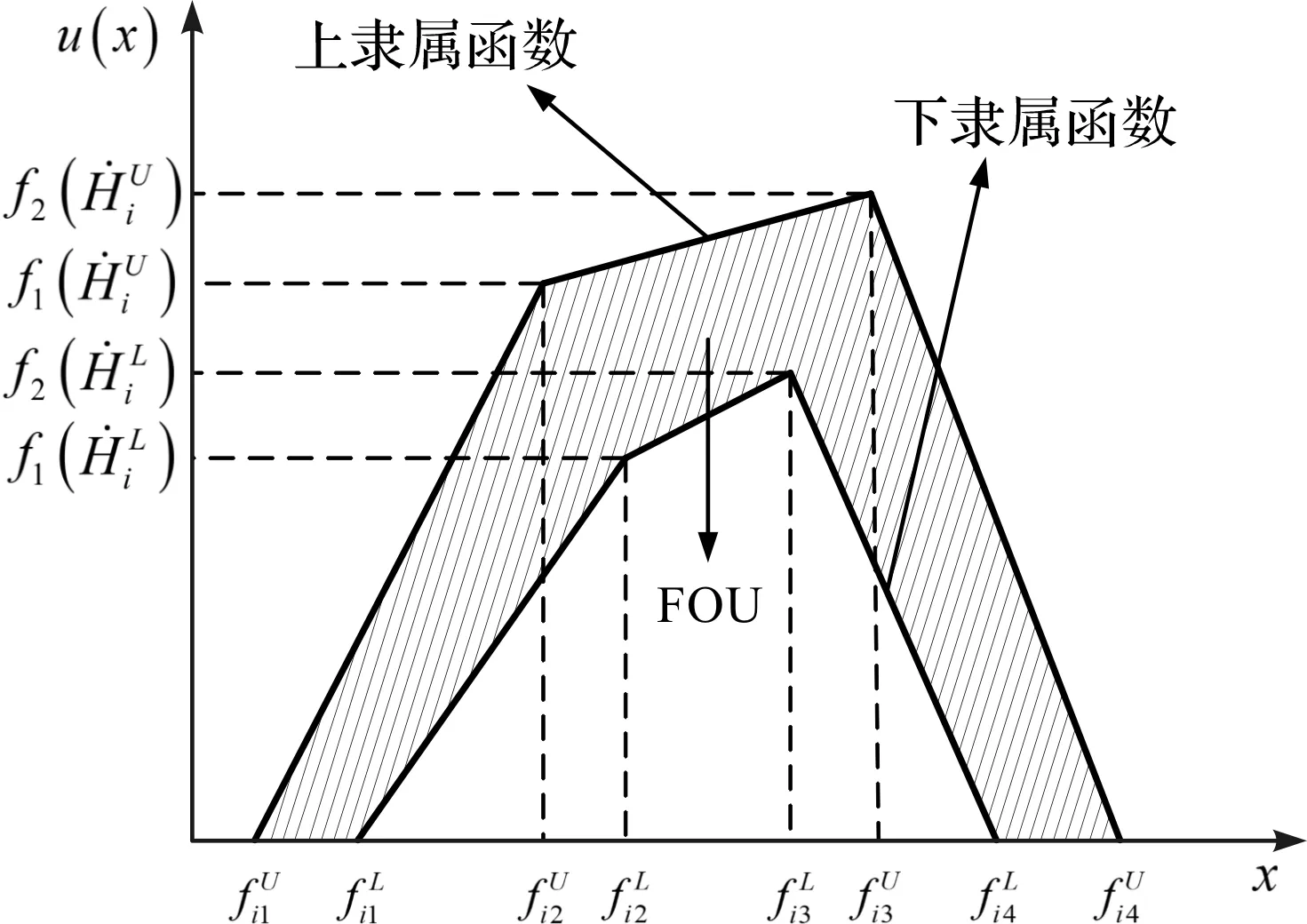
图1 IT2TFSs的数学模型
图1中,IT2TFSs由上下两个隶属度函数表示,阴影部分为不确定覆盖域。
1.2 IT2TFSs的运算方法
(3)
(4)
(5)
2 基于IT2FSs-FAHP-FCE的评价模型
针对轮系传动方案的评价,笔者提出了IT2FSs-FAHP-FCE的评价模型。
为解决指标权重难以确定的问题,笔者采用FAHP法进行指标权重赋予;为消除FAHP法的极端数据的影响,采用区间二型依赖有序加权平均(interval type-2 dependent ordered weighted average,IT2DOWA)算子,对FAHP法进行改进;为解决评价指标数据的不可公度性问题,采用概率统计结合FCE的方法,将轮系传动方案从定性转换为定量化评价。
2.1 基于IT2FSs的FAHP法的赋权方法
指标权重的分配是方案评价的关键问题,旨在表示各评价指标的重要程度。FAHP法是在层次分析法基础上,考虑到对复杂事物判断的模糊性,引入模糊判断矩阵的决策方法。该矩阵需要对指标进行成对比较,比较结果无法体现指标间的不确定性信息;而将IT2FSs与FAHP法相结合,则可以捕捉评价过程中相关的不确定性。
赋权方法的步骤如下:
1)采用IT2TFSs描述指标间相对重要性的成对比较判断。相对重要性的语言术语及其相应的IT2TFSs如表1所示。

表1 相对重要性语言标度表
2)对各指标的相对重要性进行成对判断,得到个体判断矩阵如下:
(6)

3)个体判断矩阵的聚合是达成群体共识的必要条件。个体判断矩阵经聚合后形成的群判断矩阵对指标权重的求解结果影响很大,为构建更合理的群判断矩阵,笔者采用IT2DOWA算子对多个个体判断矩阵进行聚合,以消除不公平的输入参数对聚合结果的影响。
该算子可表示为:
(7)
式中:ωπ(k),k=1,2,…,n为消除极端数据的权重因子;(π(1),π(2),…,π(n))为1,2,…,n的排列。
权重因子根据下式计算:
(8)

其中:
(9)

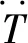
(10)

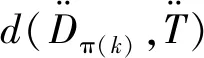
(11)
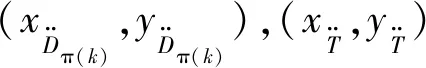

(12)
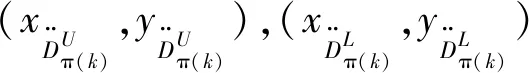

(13)
(14)
4)基于可能度矩阵求解指标权重。第i个指标的去模糊化权重的表达式为:
(15)
式中:m为指标的个数;Ranki为由可能度矩阵P计算的排序值。
Ranki可由下式求得:
(16)
式中:pij为可能度矩阵P中第i行第j列的元素值。
可能度矩阵P表达式如下:
(17)
(18)
式(18)中,Y值表达式如下:
(19)


(20)

len值可由式(21)~式(24)计算得到:
(21)
(22)
(23)
(24)
2.2 基于概率统计-FCE的综合评价方法
针对评价过程中多源异构性指标的无法公度及模糊评价指标的不可量化问题,笔者提出了结合概率统计与FCE的方法,对轮系传动方案进行定量化评价;采用引入综合评价等级隶属关系的方式概率化综合决策矩阵,并结合以广义模糊合成算子为基础的FCE方法,进行最终的评价,步骤如下:
1)评价等级隶属集合中元素类型的不同,因此每个指标的评价结果是综合评价等级隶属集合T={A(极好),B(好),C(一般),D(差),E(极差)}的模糊集,其表达式如下:
(25)
式中:m为隶属等级维度;n为评价指标数量;rij为指标uj对评价等级隶属集合的隶属等级,且各指标的评价等级隶属集合满足归一化条件;
2)采用概率统计的方法,构建子指标集U={u11,u12,…,u43}到综合评价等级隶属集合T上的综合决策矩阵R=(rij)5×15;
3)采用模糊运算将子指标集U上的综合评价集合,转换为综合评价等级隶属集合上的综合决策集合。假设子指标全局权重向量W={ω11,ω12,…,ω43},根据2.1节求解的指标权重,则子指标集U中所有指标的综合评价结果如下:
E=W°RT=(p1,p2,…,pm)
(26)
式中:°为模糊合成算子;pi为被评价方案相对于评价等级隶属集合中第i个元素的隶属度值。
笔者采用加权平均型模糊合成算子进行模糊运算,该算子的定义如下:
(27)
式中:⨁为有界积运算,即a⨁b=min(1,a·b);
4)为了使评价结果定量化表达,针对综合评价等级隶属集合,设定相应的评价分数隶属集合P={100,80,60,40,20};将综合评价结果E与评价分数隶属集合P作乘法运算,可得到最终的定量化综合评价分数值。
3 轮系传动方案综合评价
首先,笔者对轮系传动方案的评价指标进行研究,建立评价指标体系,以用于方案评价;然后,考虑到评价指标数据不唯一,导致建立的评价模型无法用于方案评价的问题,采用评价函数对其进行聚合处理;最后,基于第2节建立的IT2FSs-FAHP-FCE综合评价模型,对某轮系传动方案进行评价。
3.1 基于IT2FSs的FAHP方法赋权
针对轮系传动的关键部件(齿轮、轴、轴承及箱体),笔者从静态特性、动态特性及结构特征等方面出发,综合考虑各种影响因素,以确保评价指标集合的完整性,构建了轮系传动方案的评价指标集合,如表2所示。
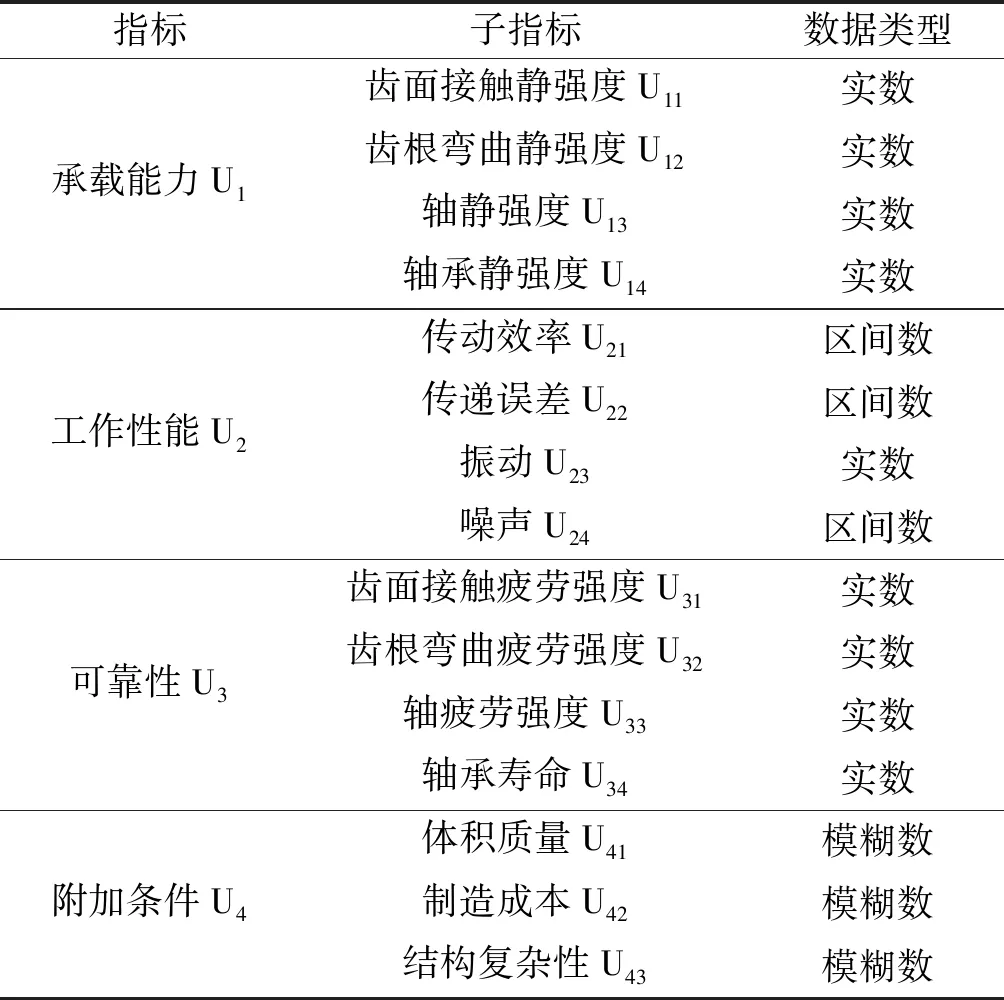
表2 轮系传动方案的评价指标集合
笔者根据评价指标集合及表1所示的相对重要性语言标度表,结合实际使用需求,由式(6)构建指标和子指标的个体判断矩阵。其中,指标的个体判断矩阵如表3所示。

表3 指标的个体判断矩阵
指标U1中子指标的个体判断矩阵如表4所示。

表4 指标U1中子指标的个体判断矩阵
指标U2中子指标的个体判断矩阵如表5所示。

表5 指标U2中子指标的个体判断矩阵
指标U3中子指标的个体判断矩阵如表6所示。

表6 指标U3中子指标的个体判断矩阵
指标U4中子指标的个体判断矩阵如表7所示。

表7 指标U4中子指标的个体判断矩阵
联立式(7)~式(14),对个体判断矩阵进行聚合,并联立式(15)~式(24),笔者计算各评价指标的可能度矩阵以导出排序值,得到归一化的权重,如表8所示。
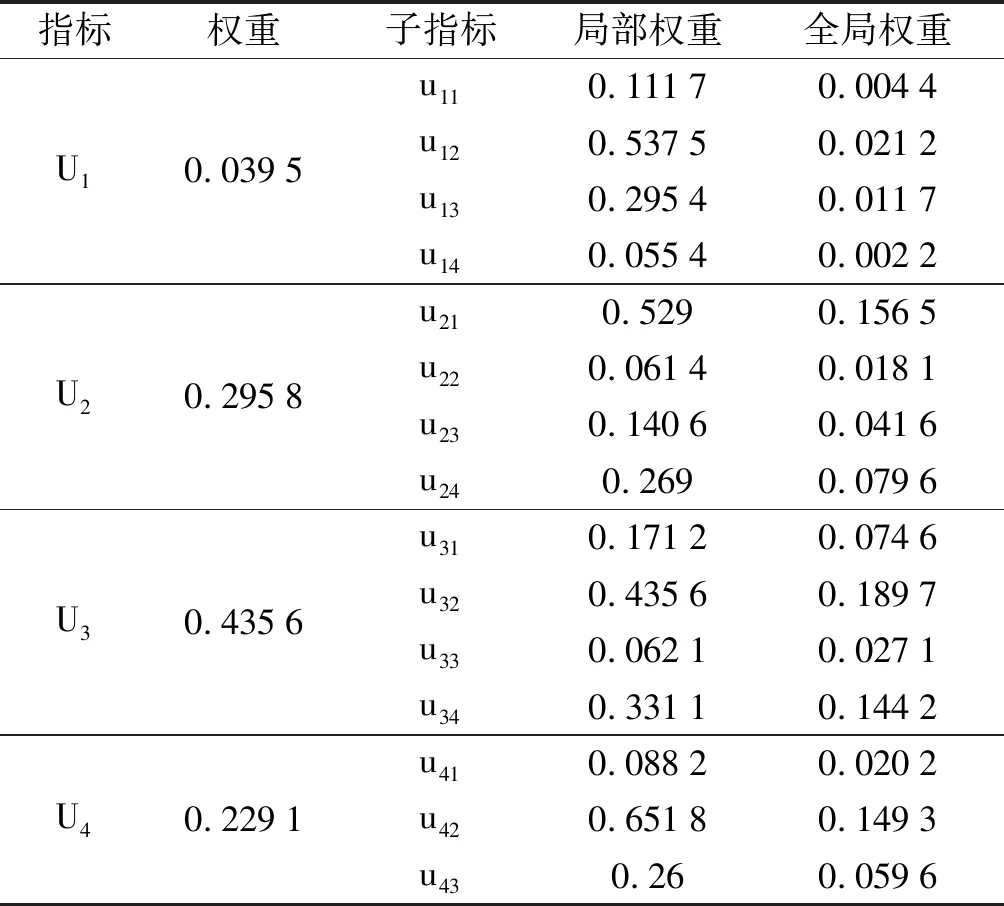
表8 指标与子指标的权重
3.2 评价指标数据的预处理及方案的评价
笔者以某企业设备选择轮系传动方案为例,采用仿真分析获取减速器方案的评价指标数据,并对其进行预处理。
被评价的单级圆柱齿轮组串联两级NGW行星齿轮组的传动方案,如图2所示。
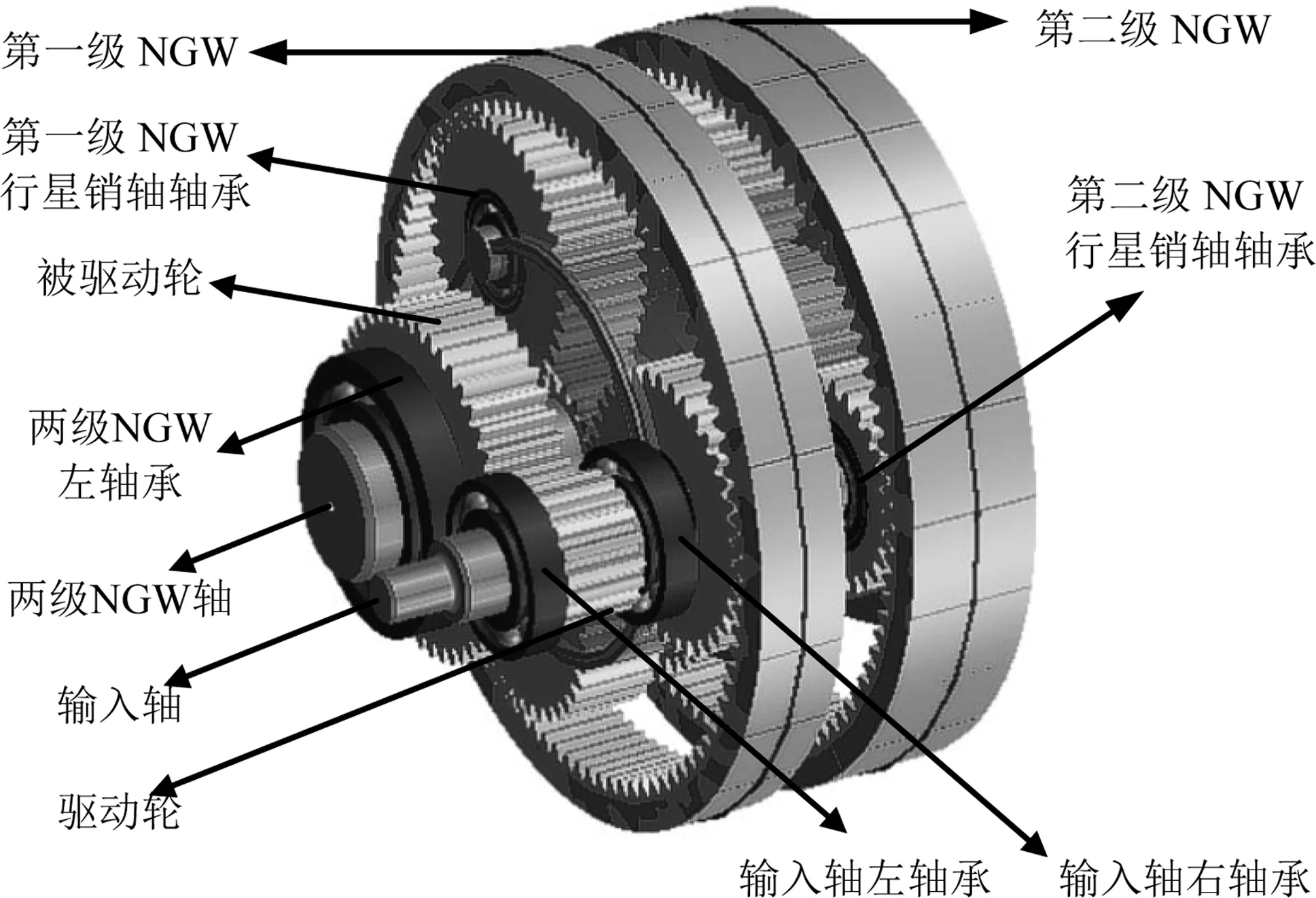
图2 传动方案的三维模型
齿轮、轴及轴承部件的评价指标属于强度分析。经综合考虑,笔者选择安全系数作为其指标数据。利用仿真获取主要受载齿轮、轴、轴承部件的静态和疲劳安全系数。对于传动效率评价指标,笔者主要考虑齿轮啮合摩擦损失、轴承摩擦损失及搅动损失。在分析传递误差时,误差波动范围变化越小越好,因此,将传递误差的峰峰值作为其评价指标的数据。振动评价指标则考虑齿轮传动系统箱体的低阶固有频率,求解箱体预应力模态,提取箱体的前六阶固有频率。基于箱体的模态分析,对箱体的声学辐射进行仿真,将得到的箱体周围场点的辐射噪声分贝数值作为噪声评价指标的数据。
由于轮系中存在着同属性部件或具体部件的指标数据不唯一等问题,导致指标数据无法进行量化。
为了将指标数据导入综合决策矩阵,笔者通过建立评价函数对指标数据进行聚合,构建的评价函数如下:
(28)
式中:n为所考虑的评价指标数据的总数;Si(x)为当前评价指标数据;Smax,Smin分别为评价指标数据中的最大值,最小值;p为惩罚系数(p≥2)。
为了能全面地获取传动系统整个工况的评价指标数据,以提高综合评价结果的准确性,笔者对整个工况载荷谱区间进行离散,即在额定功率为2 700 kW的基础上,将额定转速1 000 r/min划分为10个子工况,步长为100 r/min。
仿真分析的结果如表9所示。
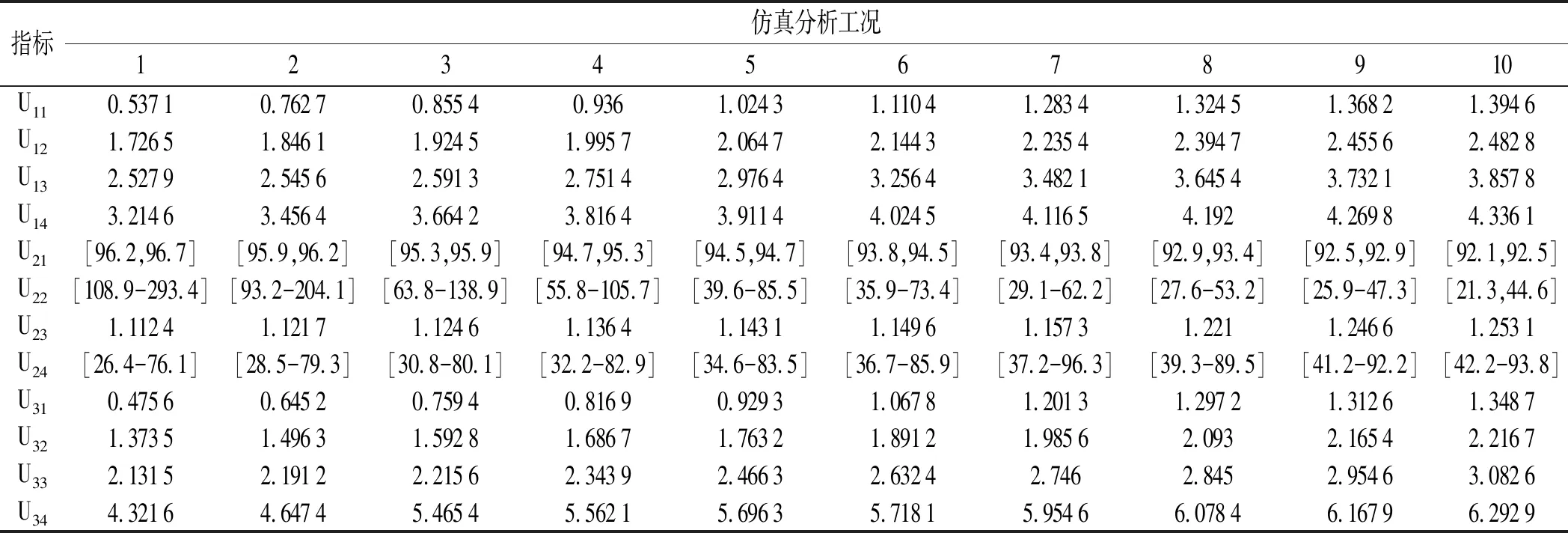
表9 仿真分析结果数据
根据仿真分析结果,并结合概率统计法,笔者构建子指标集U={u11,u12,…,u43}到综合评价等级隶属集合T上的综合决策矩阵R=(rij)5×15。
综合决策矩阵如表10所示。

表10 综合决策矩阵
笔者应用式(26)对子指标全局权重向量与综合决策矩阵进行模糊运算,得到综合评价结果E;并根据2.2节设定的评价分数隶属集合P={100,80,60,40,20},对综合评价结果E与评价分数隶属集合P进行乘法运算,可得最终的定量化综合评价分数值为62.53。
上述结果说明,该方案的综合评价结果良好,但仍然不是最优结果。
4 综合评价模型的鲁棒性分析
为验证构建的综合评价模型的有效性,笔者根据操纵权重系数的变化情况,对其进行鲁棒性分析,评估权重系数最大的指标对模型排序性能的扰动。
1)在进行鲁棒性分析前,应确定分析的敏感区的性质(全局性、局部性)。考虑到综合评价的广泛性特点,鲁棒性分析的层次结构是从总体到具体范围的全局加权,因此,关注的权重分配应是全局的;
2)定义用于鲁棒性分析的区域内所有分析集:S(鲁棒性分析过程中考虑的权重集)、I(鲁棒性分析过程中变化的权重集)、U(鲁棒性分析过程中不变的权重集)。笔者只关注单向的鲁棒性分析,因此,集合S只包含单一权重,选取影响最大的指标用于分析。对于不变的权重集,其权重变化对评价结果影响很小,因此不作考虑。除以上2个权重集之外的权重则组成变化的权重集。
综上所述,根据评价指标体系构建的分析集如下所示:
S={ω32},
I={ω21,ω23,ω24,ω31,ω34,ω42,ω43},
U={ω11,ω12,ω13,ω14,ω22,ω33,ω41}
3)设定弹性系数,用来表示与最重要指标的权重变化有关的其他权重系数的相对补偿。
笔者设定敏感性权重的弹性系数αs,s∈S的值为1;稳定性权重的弹性系数αu,u∈U的值为0;采用比例法计算弹性权重系数αi,i∈I用来表示变化权重集中权重系数的相对补偿,表示如下:
(29)

4)在比例化情况下,根据相关的权重弹性系数,对被分析权重集所实施的变化量Δx的边界可以用下式计算:
(30)

5)在计算出边界条件后,将其划分为19份,以计算所需的步长,并根据设定的参数计算新的权重。具体的计算方法如下:
(31)

联立式(29)~式(31),得到19组用于鲁棒性分析的新权重,如表11所示。
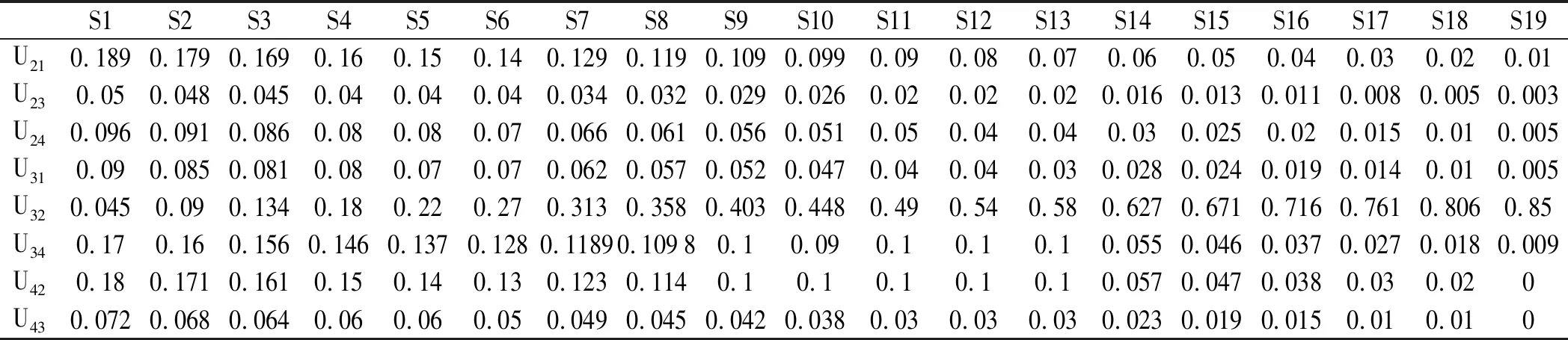
表11 新指标权重
6)因为综合评价分数值是在特定体系下的相对分数,所以只有一个方案无法体现其对照性。
为了对基于IT2FSs的轮系传动方案综合评价方法的有效性进行验证,需加入对照组进行相对分数值的分析。笔者采用rand随机数函数生成0到1上的随机实数,以构建随机矩阵,得到另外2个综合决策矩阵,将其作为对照组。
对照组1如表12所示。

表12 对照组1
对照组2如表13所示。

表13 对照组2
7)根据表11中的19组变化的权重系数,笔者计算出该方案与两个对照组的排序变化,如图3所示。

图3 排序性能的鲁棒性分析
图3中:同一方案中权重系数的变化会导致综合评价分数值的变化,不同方案中权重系数的变化会导致排序值的变化,这说明了该模型对权重系数的变化是敏感的。通过比较各组变化权重中方案的排序,可知所有方案都保持了其排名。因此可以得出结论:该案例在特定体系下的综合评价分数值是有效的,与对照组2相比,该方案有足够的优势;与对照组1相比,该方案存在不足。
由于方案的优劣主要取决于权重值较大的指标,通过对三个方案的综合决策矩阵进行分析,参考权重值较大的指标U23,可知该指标的评价等级隶属集合的隶属等级排序:对照组1>该案例>对照组2。对于对照组2,若要提高其排序,需优化综合决策矩阵,即采取有效的方法提高齿根弯曲疲劳强度,如合理选用材料和热处理方式,改进制造工艺等。
综上可知,当权重系数发生改变时,综合评价分值会出现一定的变化,但变化幅度极小,可忽略不计,且各方案的排序顺序不会改变。
由此可以表明:在权重发生较大波动时,最优轮系传动方案均为对照组1,说明该轮系传动方案综合评价模型对权重的敏感性低,且稳健性好。
5 结束语
为了解决轮系传动方案的评价问题,笔者提出了一种基于IT2FSs的轮系传动方案综合评价方法。
首先,构建了区间二型模糊集的数学表达模型,并研究了其基本的运算逻辑;其次,提出了基于IT2FSs的联合FAHP与FCE的数学评价模型;然后,构建出了包含15个评价指标的综合评价体系,并对其中指标的权重进行了确定,结合预处理后的指标数据,利用评价模型对轮系传动方案进行了综合评价;最后,为分析基于IT2FSs的轮系传动方案综合评价方法的有效性,又对其进行了鲁棒性分析。
研究结论如下:
1)采用基于IT2FSs的FAHP方法,计算得到每个指标与子指标的权重,其中指标的权重系数分别为:承载能力(0.039 5)、工作性能(0.295 8)、可靠性(0.435 6)、附加条件(0.229 1),说明对轮系传动方案的评价主要侧重于可靠性,并较少考虑承载能力;
2)采用FCE法对评价函数预处理后的指标数据进行了处理,得到方案的综合评价分数值为62.53,表明该方案的综合评价结果良好,实现了从定性到定量的方案综合评价目的;
3)鲁棒性分析中方案的排序始终为对照组1>该案例>对照组2,说明了基于IT2FSs的轮系传动方案综合评价方法的有效性。该方法可为决策者选择轮系传动方案提供科学的指导和有效的技术支持,具有较高的工程实用性。
后续研究中,笔者将从宏观角度研究轮系传动方案的综合评价,利用统计学方法离散化齿轮传动系统的尺度参数,得到齿轮传动系统的简化等效模型,并利用大数据技术对齿轮传动系统进行分析,实现齿轮传动方案的概念性综合评价目的。

