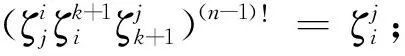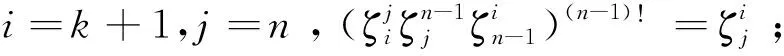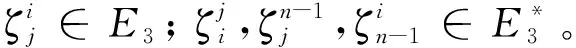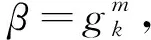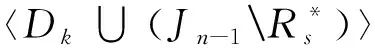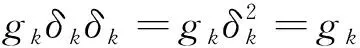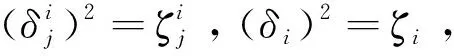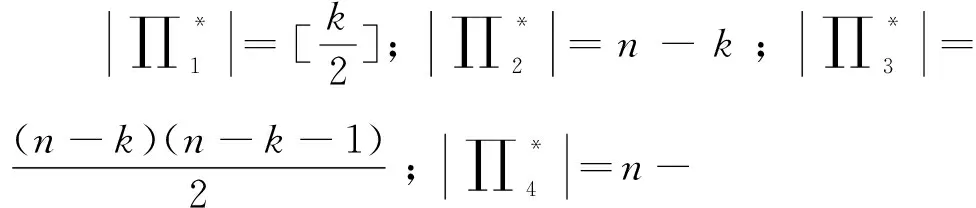半群DkPn的秩和平方幂等元秩

张建国，余江慧，罗永贵

(贵州师范大学 数学科学学院，贵州 贵阳 550025)

设S是半群,A是S的非空子集且a,e∈S。若对任意的s∈S,存在a1,a2,…,am∈A使得s=a1a2…am,则称A是半群S的生成集,记为S=〈A〉。若对半群S的任意生成集B都有|A|≤|B|,则称A为半群S的极小生成集。通常半群S的秩定义为

rank(S)=min{|A|:A⊆S,〈A〉=S},

其中|A|为A的基数。若e2=e,则称e为半群S的幂等元,半群S中所有幂等元之集记为E(S)。类似地,A中所有的幂等元之集记为E(A)。若(a2)2=a2且a2≠a,则称a为半群S的平方幂等元,半群S所有平方幂等元之集用E2(S)表示。类似地,A中所有的平方幂等元之集记为E2(A)。若A⊆E2(S)且对任意s∈S,存在b1,b2,…,bt∈A使得s=b1b2…bt,则称A为半群S的平方幂等元生成集。令M是半群S的任意平方幂等元生成集且|A|≤|M|,则称A为半群S的平方幂等元极小生成集,进而称|A|为半群S的平方幂等元秩,记为

rank2(S)=min{|A|:A⊆E2(S),〈A〉=S}。

设Xn={1,2,…,n}并赋予自然序,Pn和Sn分别是Xn上的部分变换半群和对称群,记SPn=PnSn,则SPn是Pn的子半群。令

记Dk=〈gk,δk〉,称Dk为Xn上的k-局部二面体群且令DkPn=Dk∪(PnSn),易证DkPn是半群Pn的子半群。设α∈DkPn,用im(α)表示α的象集,dom(α)表示α的定义域,ker(α)表示dom(α)上的如下等价关系:

ker(α)={(x,y)∈dom(α)×dom(α):xα=yα}。

为叙述方便,引用Green-等价关系[1-2],在半群DkPn中L,R,H,D,J有如下刻划:对任意的α,β∈DkPn有:

(α,β)∈L⟺im(α)=im(β);

(α,β)∈R⟺ker(α)=ker(β);

(α,β)∈J⟺|im(α)|=|im(β)|;

D=J。

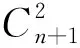
对任意的i,j∈Xn,定义R(i,j)={α∈Jn-1:iα=jα},Ri={α∈Jn-1:dom(α)=Xn{i}},易知R(i,j)=R(j,i),当3≤k≤n时,对Jn-1中的所有R-类作如下的分类:

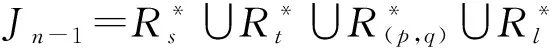
用符号ζi(1≤i≤n)表示Jn-1中如下形式的幂等元:

设n≥3,3≤k≤n,记

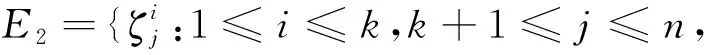
E4={ζi:1≤i≤n};

令E(Jn-1)为Jn-1中所有幂等元之集,于是有E(Jn-1)=E1∪E2∪E3∪E4且E1,E2,E3,E4两两相交为空集。记

设δ∈E(Jn-1)且δ的唯一非单点核为(i,j),其中i,j∈Xn,则Jn-1中的平方幂等元形式如下:

其中:q∈Xn{i,j};dom(δi)=Xn{i};s,t∈Xn{i}。

当n≥3,3≤k≤n,令

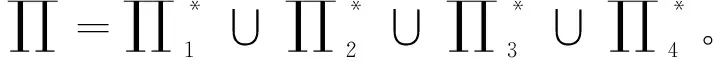
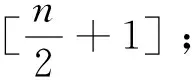
定理1设n≥3,3≤k≤n,则半群DkPn=〈{gk,δk}∪E〉。

定理3设n≥3,3≤k≤n,则半群DkPn=〈E2(DkPn)〉=〈{gkδk,δk}∪∏〉。

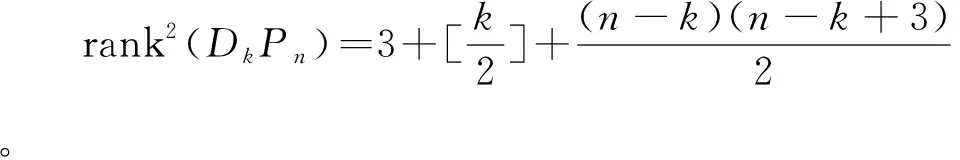
本文未定义的符号及术语参见文献[1-2]。

为完成定理1及定理2的证明先给出以下若干引理。

引理1[1]当n≥3时,SPn=〈E(Jn-1)〉。

引理2当0≤r≤n-2时,Jr⊆Jr+1·Jr+1。

证明由文献[8]引理1.3直接可得。

由引理2直接可得:

推论1设n≥3,3≤k≤n,则

DkPn⊆〈Jn-1,Dk〉。

引理3设n≥3,3≤k≤n,则

则

引理4设n≥3,3≤k≤n,则

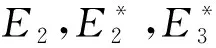
从而

又由

则

即

引理5设n≥3,3≤k≤n,则

证明对任意的k+1≤i

(1)对

引理6设n≥3,3≤k≤n,则

定理1的证明因为半群DkPn=Dk∪(PnSn)=Dk∪SPn且Dk=〈{gk,δk}〉,再由引理1知SPn=〈E(Jn-1)〉,又由于E(Jn-1)=E1∪E2∪E3∪E4且E1,E2,E3,E4两两相交为空集。由引理3知

由引理4知

引理7[10]对任意的α,β∈Pn,有dom(αβ)⊆dom(α),im(αβ)⊆im(β)。

引理8设α,α1,α2,…,αs∈Jn-1使得α=α1α2…αs,则(α,αs)∈L,(α,α1)∈R。

证明由α=α1α2…αs及引理7可知im(α)⊆im(αs),又由α,αs∈Jn-1可知(α,αs)∈J,依据格林关系有|im(α)|=|im(αs)|=n-1,故im(α)=im(αs),即(α,αs)∈L。

由α=α1α2…αs及引理7可知dom(α)⊆dom(α1),从而有|dom(α)|≤|dom(α1)|。对任意的(x,y)∈ker(α1)有xα1=yα1;进而有xα1α2…αs=yα1α2…αs,即xα=yα,故(x,y)∈ker(α),进一步ker(α1)⊆ker(α),从而|dom(α1)|≤|dom(α)|,因此|dom(α1)|=|dom(α)|。由于α1∈Jn-1,则ker(α1)有n-1个不同的同余类,不妨设为a1ker(α1),a2ker(α1),…,an-1ker(α1),则a1ker(α1),a2ker(α1),…,an-1ker(α1)∈dom(α)/ker(α)。此外,a1ker(α)∪a2ker(α)∪…∪an-1ker(α)=dom(α);a1ker(α1)∪a2ker(α1)∪…∪an-1ker(α1)=dom(α1)。现假设|aiker(α1)|<|aiker(α)|,其中i∈{1,2,…,n-1},故|dom(α1)|=|a1ker(α1)|+|a2ker(α1)|+…+|an-1ker(α1)|< |a1ker(α)|+|a2ker(α)|+…+|an-1ker(α)|=|dom(α)|。与|dom(α1)|=|dom(α)|矛盾。故|aiker(α1)|=|aiker(α)|,即有ker(α)=ker(α1),故而(α,α1)∈R。

由引理8直接可得:

推论2设A⊆Jn-1且Jn-1=〈A〉,则A覆盖Jn-1中的每一个R-类和每一个L-类。

引理9设n≥3,3≤k≤n,对任意的β∈Dk有:

容易计算:

引理10设n≥3,3≤k≤n,A⊆Dk∪Jn-1且Dk∪Jn-1=〈A〉,则:

(1)|A∩Dk|≥2。

证明(1)若|A∩Dk|=∅,由A⊆Dk∪Jn-1可得A⊆Jn-1,进而有〈A〉⊆〈Jn-1〉=SPn,与〈A〉=DkPn矛盾,故|A∩Dk|≠∅;若|A∩Dk|=1,不妨设A∩Dk=α,则〈A∩Dk〉=〈α〉是循环群,即〈α〉是交换群,与Dk是非交换群矛盾,故而|A∩Dk|≥2,(1)得证。

推论3rankDkPn≥

证明由引理10可得:

反之,由推论3知:

为完成定理3及定理4的证明先给出以下引理。

引理11设n≥3,3≤k≤n,Dk的极小生成集为{gkδk,δk},即Dk=〈{gk,δk}〉=〈{gkδk,δk}〉,且gkδk,δk均为平方幂等元。

从而

gkδk,((gkδk)2)2=(1Xn)2=1Xn=(gkδk)2;故gkδk是平方幂等元。同理可证(δk)2=1Xn≠δk,((δk)2)2=(1Xn)2=1Xn=(δk)2,即δk是平方幂等元。

DkPn=Dk∪SPn=〈{gkδk,δk}∪∏〉。

由定理3及推论3可得

特别地,类似上述证明可得:当k=1时半群DkPn=D1Pn且