Physical generation of random numbers using an asymmetrical Boolean network*
Hai-Fang Liu(刘海芳) Yun-Cai Wang(王云才) Lu-Xiao Sang(桑鲁骁) and Jian-Guo Zhang(张建国)
1Key Laboratory of Advanced Transducers and Intelligent Control System,Ministry of Education,Taiyuan University of Technology,Taiyuan 030024,China
2College of Physics and Optoelectronics,Taiyuan University of Technology,Taiyuan 030024,China
3Guangdong Provincial Key Laboratory of Photonics Information Technology,Guangzhou 510006,China
4School of Information Engineering,Guangdong University of Technology,Guangzhou 510006,China
Keywords: autonomous Boolean networks,random numbers,chaos,unpredictability
1. Introduction
Random numbers are important in many fields, such as identity recognition,[1-3]Monte Carlo simulations[4,5]and information encryption.[1,6,7]In those applications, the quality of random numbers is extremely significant. Especially in information encryption, randomness and unpredictability of random numbers are the key factors to ensure information security.[1,6,7]
Random number generators may be divided into pseudorandom number generators and physical random number generators. The pseudorandom numbers are generated by algorithms, which can produce random numbers with high speed and good distribution characteristics.[8,9]However,the unpredictability of pseudorandom numbers is determined by the seeds of the algorithm,i.e.,the sequence of random numbers is deterministic and can be generated repeatedly as long as the seeds are fixed.[1]The physical random numbers are generated by extracting and quantifying the random characteristics of physical processes. The optical physical random number generators (PRNGs) feature the highspeed physical generation of random numbers due to the high speed of optical devices.[10]On the other hand, electrical random numbers are more widely used because they are inexpensive and easily integrated. Entropy sources of electrical PRNGs include noise, metastability, oscillator and chaos. The PRNGs based on noise directly amplify and extract the noise from a device, and the entropy source is genuinely random, but the amplitude of the noise is so small that a strong amplifier is needed, thereby introducing a 0-1 bias and increasing the power consumption.[11-13]The PRNGs based on metastability obtain random numbers from a metastable system, which produces two stable states with equal probability. However,it is hard to obtain perfectly balanced probabilities, and thus a 0-1 bias is introduced.[14,15]The PRNGs based on oscillations extract random numbers by sampling phase jitter from an oscillator.[16,17]The PRNGs based on chaos obtains random numbers from physical chaotic systems, in which noise is amplified rapidly by chaos.[18,19]Chaotic PRNGs have become standard in the field because of their sensitivity to noise,broadband features,and large amplitude.[1]
Boolean chaos produced by ABN has been widely addressed in recent years. In 2009, Zhang Ruiet al.[20]realized an ABN by using a logical circuit and observed chaos in experiment. The chaotic bandwidth may be on the order of GHz (−10 dB), which largely outperforms the existing electrical sources.[20]In ABN-based chaotic systems,all nodes of the network may produce chaos,i.e.,there are at least 2 positive Lyapunov exponents, thus leading to complex dynamics. The ABN chaotic system is composed of digital logic devices, which have a simple structure and are easy to integrate in comparison with other hyperchaotic systems, whose hardware implementation requires analog devices such as resistances, capacitances or inductances.[21-23]Boolean chaos,due to its advantages of low power consumption, wide bandwidth and easy integration, has been successfully applied to random numbers generation.In 2013,Rosinet al.proposed an ABN-based PRNG composed of fifteen 3-input logical XOR gates and one 3-input logical XNOR gate.[24]In 2017, Donget al. improved the architecture,showing that only four nodes,instead of six, may be used to produce chaotic oscillations.However, to fabricate a random number generator, 16 logical gates are necessary.[25]In 2018, MAet al. proposed a new PRNG based on an ABN with 7 3-input logical gates, thus reducing the power consumption.[26]However,their device is prone to 0-1 bias and should employ an XOR chain for postprocessing. The 2-input logical gates may reduce power consumption because they use fewer CMOS MOSFETs or transistors than 3-input logical gates. In 2015,Parket al. developed a PRNG based on an ABN composed of one 2-input logical XNOR gate and 32 inverters.[27]The generated random numbers can pass the NIST tests after a post-processing. In 2019,Zhanget al. proposed a PRNG based on an ABN composed of 15 2-input logical gates, it can generate random numbers passing the NIST tests without post-processing.[28]However,the oscillations of the ABN are dependent on the delay time along links,because of the symmetric structure.
In this paper,an aABN with asymmetric topology is proposed. Its main advantage is the reduction in power consumption due to the reduction in the number of nodes. The PRNG based on the proposed aABN produces random numbers passing the NIST tests without post-processing. The rest of this paper is structured as follows. Results from numerical simulations are presented in Section 2, showing that the oscillation of the aABN is independent of the incommensurate delays along links. In Section 3, we describe the experimental implementation of the aABN on an FPGA(Chip: Altera Cyclone IV FPGA, EP4CE10F17C8N), and discuss experimental results,showing that the chaotic features are comparable to those obtained from symmetric ABNs,e.g.those suggested in Refs.[24,28],with a reduced number of logical gates. In Section 4, a novel aABN-based RNG is proposed. We generate 1 Gbit of data(1000 sequences of 1 Mbit)and prove they can pass the NIST test suite successfully. The unpredictability of random numbers is also analyzed by repeatedly restarting the RNG. Finally, in Section 5, we draw some conclusions from the present study and also present the perspectives in this research topic.
2. Asymmetrical autonomous Boolean network model
The structure diagram of the aABN is shown in Fig.1(a).For comparison, figures 1(b)and 1(c)show the structure diagrams of the symmetric ABNs proposed in Refs. [24,28]. In the following, ABNs of Figs. 1(b) and 1(c) will be referred to as sABN1 and sABN2, respectively. In Fig. 1, each node represents a logical gate, node 0 executes logic XNOR while the other nodes execute logic XOR,τi jrepresents the delay time along the link from nodejto nodei. The number of nodes in aABN, sABN1, and sABN2 are 12, 15, and 16, respectively. Each node in aABN and sABN1 have two inputs from other nodes, while each node in sABN2 has three inputs from two other nodes and one self-feedback. Each node in sABN1 and sABN2 are coupled with their adjacent nodes,leading to a symmetric structure. The topology of aABN is asymmetric instead,because nodes 7,8 and node 0,1 are not mutually coupled.
The mathematical model of aABN is shown as follows:
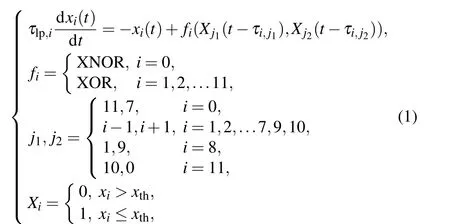
whereτlp,iis the response characteristic parameter of the logical gatei, which regulates the response speed of the logical gate,xidenotes the output of nodei,τijrepresents the delay time along the link from nodejtoi,fiis the logical function of nodei, andXiis 0 or 1, depending on whetherxiis below or above a given thresholdxth. The threshold is set to bexth=0.5 in the simulations,and it is determined by the logical gate itself in experiment.
Looking at the results of simulated experiments, we see that the oscillations of ABNs are sensitive to the delay time along links. The oscillation amplitudes of some nodes of sABN1 and sABN2 are very small, and some nodes do not even oscillate when the parametersτijare assumed to be the same value. In order to make a comparison, the oscillations of aABN, sABN1, and sABN2 are observed under the identicalτi j. The simulation results are shown in Fig. 2. In this simulation,we assumeτlp,i=0.35 ns andτij=0.05 ns. Time series of aABN,sABN1,and sABN2 are shown in Figs.2(a),2(b), and 2(c), respectively. It may be seen that the output waveforms of symmetric nodes of sABN1 and sABN2 are identical: in Fig. 2(b) we havex1(t)=x14(t),x2(t)=x13(t),x3(t) =x12(t),x4(t) =x11(t),x5(t) =x10(t),x6(t) =x9(t),andx7(t) =x8(t), and in Fig. 2(c) we havex1(t) =x15(t),x2(t)=x14(t),x3(t)=x13(t),x4(t)=x12(t),x5(t)=x11(t),x6(t)=x10(t), andx7(t)=x9(t). As shown in Fig. 2(a), almost every node oscillates between 0 and 1 with a large amplitude,only node 1 has a small amplitude of oscillations.Figure 2(b)shows that the outputs of ten nodes are stable,whereas those from the other five nodes oscillate slightly. In Fig.2(c),we may see three nodes with stable output,whereas the other 13 nodes oscillate. The amplitudes are smaller than those of aABN as shown in Fig.2(a).The outputs are also observed for different values ofτi j. When the parametersτijare equal,the oscillation amplitudes of sABN1 and sABN2 increase withτijincreasing. However,the performances of sABN1 and sABN2 are worse than those of aABN. If the parametersτijchanges withiandj(incommensurately),all nodes of aABN,sABN1 and sABN2 can produce large amplitude oscillations. We observe that our aABN always oscillates independently of the choice ofτijchanges. In particular, the oscillations of aABN are independent of the incommensurate time delays and logical gates.

Fig.1. Structure diagrams of(a)aABN,(b)sABN1,and(c)sABN2.
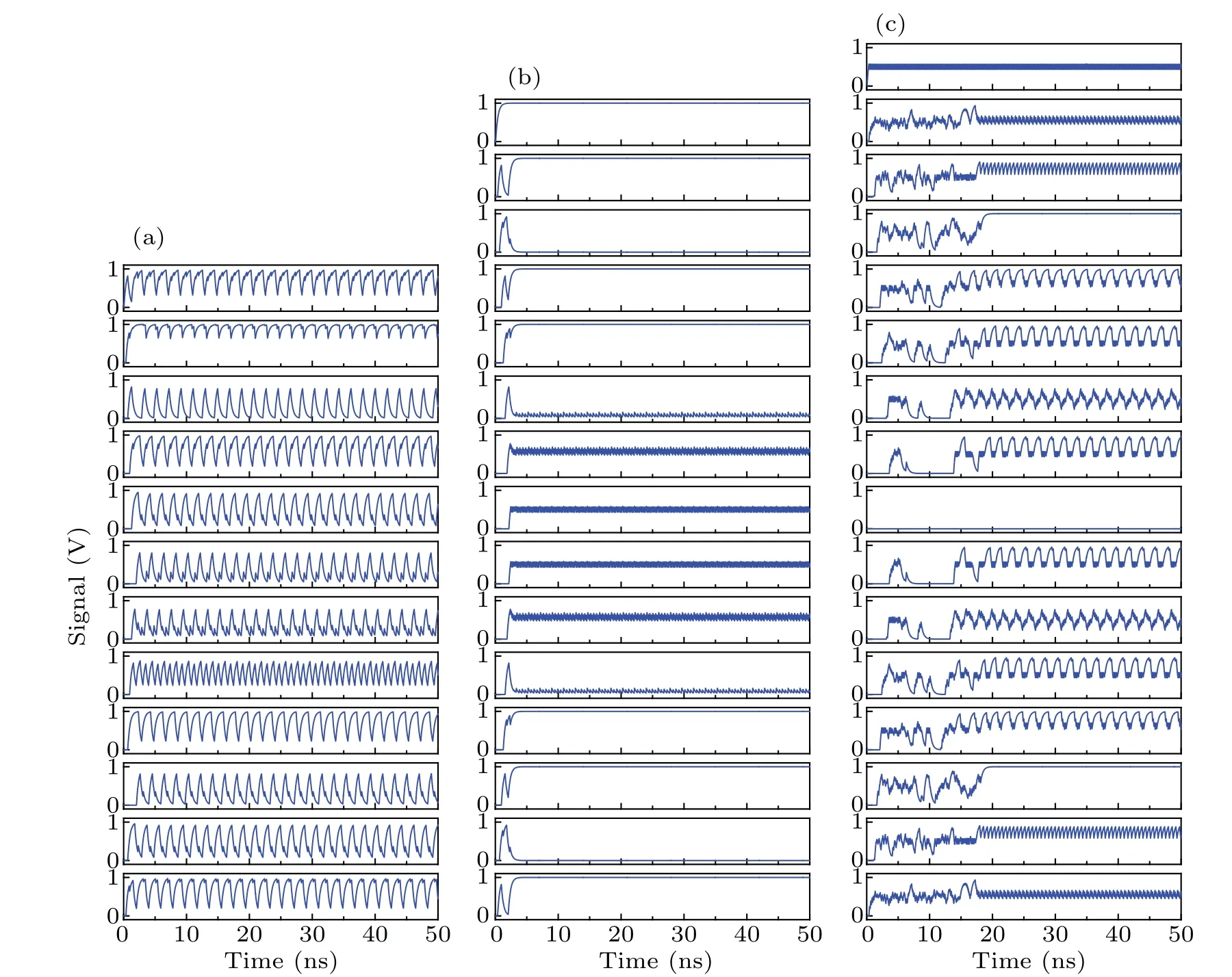
Fig.2. Simulation results: (a)time series of aABN,(b)time series of sABN1,(c)time series of sABN2.
3. Experimental results
In our experiments, aABN, sABN1, and sABN2 are implemented on the same FPGA.There are no additional delays,i.e.,eachτijis the delay of the connection line in the FPGA.Figure 3(b) shows a schematic diagram of the experimental device,which includes a computer,an FPGA chip and an oscilloscope. The FPGA implementation includes 4 steps:
(i)the Verilog program code is written(see Fig.3(a)),realizing the function in formula(1);
(ii)the Verilog program is compiled to generate the JTAG Indirect Configuration File;
(iii)the JTAG Indirect Configuration File is downloaded to FPGA chip. Figure 3(c)shows the RTL circuit diagram of FPGA,where net~idenotes nodei,i.e.,XOR gate fori=1-11, and XNOR gate fori=0, net[i] is buffer fori=0-11,wordout0 denotes the outputxi,takingxi=x0for example in the picture;
(iv) the output data are observed and collected through the oscilloscope connected to the FPGA.

Fig.3. (a)Verilog program code of Eq.(1),(b)schematic diagram of experimental device,and(c)RTL circuit diagram of FPGA.
Experimental results show that all nodes of aABN,sABN1, and sABN2 can produce chaos. Taking the outputs of node 0 for example, experimental results are shown in Fig. 4. Figures 4(a1), 4(b1), and 4(c1) show that time series from aABN, sABN1, and sABN2 are chaotic. Figures 4(a2), 4(b2), and 4(c2) display the distributions of the output voltage amplitudes: one may see a double-peak structure with maxima at high(1 V)level and low(0 V)level. Indeed,the digital logical gates’0-1(1-0)transition process is very short and the output sequences are close to binary. The largest Lyapunov exponent is a popular method to measure chaos.[20,29]The largest Lyapunov exponentλis the slope of the red line shown in each of Figs. 4(a3), 4(b3), and 4(c3),i.e., λ= (ln(d(s))−ln(d(0)))/s.[20]Values ofλare larger than 0,indicating that outputs of aABN,sABN1,and sABN2 are all chaotic. The corresponding autocorrelation functions are shown in Figs. 4(a4), 4(b4), and 4(c4), the full widths at half height are about 0.5 ns. There is no significant difference among the spectra shown in Figs.4(a5),4(b5),and 4(c5),the−10-dB bandwidths are about 600 MHz. These results show that the chaotic features of aABN are comparable to those of sABN1 and sABN2, however, they are obtained with a reduced number of gates,and thus requiring less power.
Permutation entropy is an effective method to measure the complexity of time series.[30]Figure 5 shows the plots of permutation entropyH versusembedded delayτdof the outputs from aABN, sABN1, and sABN2, where the embedded dimensions are all set to be 5.The permutation entropy of aABN and sABN1 are very close and higher than that of sABN2.
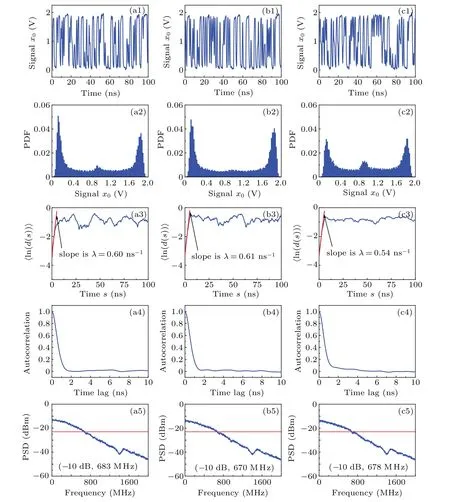
Fig. 4. Time series, distribution, the largest Lyapunov exponents, autocorrelation functions, and spectra of the output voltage amplitudes of[(a1)-(a5)]aABN,[(b1)-(b5)]sABN1,[(c1)-(c5)]sABN2.
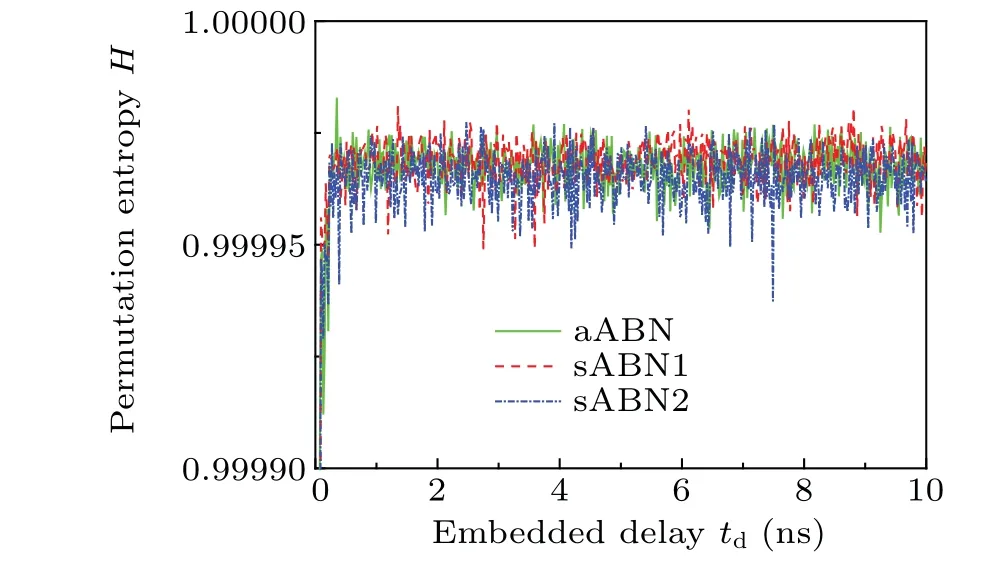
Fig.5.Permutation entropy H versus embedded delay td for aABN,sABN1,and sABN2.
4. A random number generator based on proposed aABN
The experimental results show that aABN may be used as the entropy source of RNG,i.e.,the double-peak curve at high (1 V) and low (0 V) levels may be exploited to extract random numbers. Figure 6 shows the structure of our RNG with using the aABN as an entropy source. The sampling and quantization process just use a flip-flop, because the output approximates a binary sequence. In order to eliminate any potential 0-1 bias and to generate high-quality random numbers,the outputs of nodes 1,2,5,9 are extracted for XOR.

Fig.6. Schematic diagram of random number generator based on aABN.
The RNG is implemented on an FPGA, the clock frequency is set to be 100 MHz, and experimental results are shown in Fig. 7. Figure 7(a) shows a random numbers sequence: the minimum pulse width is 10 ns, the amplitude is 0-2 V. The grayscale dot matrix graphic of the sequence is shown in Fig. 7(b), and provides a qualitative assessment of the sequence randomness. It shows no obvious pattern, indicating that the random numbers are aperiodic. The NIST statistical test suite is the international common random number test standard with a“passed”threshold requiring aP-value larger than 10−4and a proportion larger than 0.98. We generate 1 Gbits of data for the NIST tests, and all 15 tests are passed. Results are shown in Table 1. From these experimental results,we conclude that our aABN-based RNG is able to generate at least 100-Mbit/s random numbers passing NIST tests.
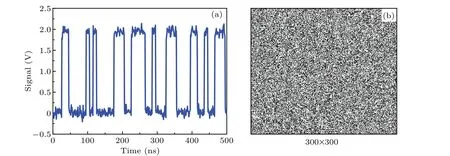
Fig. 7. (a) Random number sequences and (b) grayscale dot matrix graphics of 90000 random numbers rearranged into a 300 ~300 square matrix,black represents 1 and white represents 0.

Table 1. Results of NIST statistical test suite.
Unpredictability is another important property of random numbers.To analyze the unpredictability of the aABN entropy source, the RNG is repeatedly restarted in the same experimental conditions and the chaotic sequences are observed.[31]Figure 8 shows the experimental results,and figure 8(a)shows that the restarting sequences for each restarting time series of 80 ns are generated. The initial values of all nodes are set to be at a low level (0 V) which is maintained for 10 ns, which is shown in the gray shadowed region. After this stage, the RNG begins to evolve. Figure 8(b) shows 100 restarting sequences: we cannot see any repeating structure after the 10-ns initial time and the 10-ns dispersed time, indicating that the values of each restarting sequence are different and random after the short autonomous evolution time. Shannon entropy is used to evaluate the randomness.[32]Figure 8(c)shows the Shannon entropy of 1000 restarting random number sequences,and Shannon entropy is 0 because the sequences are the same before 10 ns. Then,Shannon entropy increases with time increasing and approaches to 1 at about 20 ns, it fluctuates slightly after 20 ns.We conclude that the random numbers generated by RNG based on the aABN are unpredictable.

Fig.8. Restarting experimental results,showing(a)restarting chaotic sequences,(b)map of restarting sequences 100 times,and(c)Shannon entropy of restarting sequences 1000 times.
5. Conclusions and perspectives
In this paper, an aABN composed of 12 nodes is proposed and its performance is analyzed in detail. Simulation results indicate that the oscillations of the aABN do not depend on the incommensurate time delays along links. Experimental results show that our aABN may offer performance comparable to that of sABN1 and sABN2 in terms of the the largest Lyapunov exponents,spectra,autocorrelation function,and permutation entropy,however with using a reduced number of nodes. Thus, it is instrumental in reducing the power consumptions of ABN systems. A novel aABN-based RNG is also proposed and experimentally implemented on an FPGA.Experimental results show that our RNG may generate random numbers passing NIST statistical tests suite at 100 Mbit/s.Compared with the RNG proposed in Refs.[24,28],the power consumption of our RNG is reduced due to the reduced number of required logical gates. Experimental results also show that the output sequences generated after 10 ns of autonomous evolution follow totally different trajectories,i.e., the generated random numbers are unpredictable.
Acknowledgment
The authors would like to express their gratitude to EditSprings(https://www.editsprings.com/)for providing the expert linguistic services.
- Chinese Physics B的其它文章
- Numerical investigation on threading dislocation bending with InAs/GaAs quantum dots*
- Connes distance of 2D harmonic oscillators in quantum phase space*
- Effect of external electric field on the terahertz transmission characteristics of electrolyte solutions*
- Classical-field description of Bose-Einstein condensation of parallel light in a nonlinear optical cavity*
- Dense coding capacity in correlated noisy channels with weak measurement*
- Probability density and oscillating period of magnetopolaron in parabolic quantum dot in the presence of Rashba effect and temperature*

