Dense coding capacity in correlated noisy channels with weak measurement*
Jin-Kai Li(李进开), Kai Xu(徐凯), and Guo-Feng Zhang(张国锋)
School of Physics,Beihang University,Beijing 100191,China
Keywords: correlated noise channel,quantum dense coding,weak measurement,reversal measurement
1. Introduction
Since the concept of quantum dense coding (sometimes called superdense coding)was first introduced by Bennett and Wiesner,[1]this field has been discussed widely.To realize this communication protocol, it is essential to share an entangled state between the sender (Alice) and receiver (Bob) initially.The entangled state has the property that can be transformed by the sender into another state via a local operation by taking some sets of operations. Then Alice transmits her qubit to Bob,who performs an measurement on the global state together with the received qubit and his original one. The signal state that Alice sent is distinguished unambiguously by the measurement. Thus,the sending of one single qubit transmits two bits of classical information.This is absolutely impossible without entanglement;the amount of information conveyed by an isolated qubit cannot exceed one bit. Mattleet al.[2]have experimentally realized quantum dense coding in optical experiments on polarization-entangled photons.
It is straightforward to focus on the amount of classical information that a quantum state can reliably transmit,i.e.,the subsequent intensive dence coding capacity. It has been proved that for noiseless channels and unitary encoding, the dense coding capacity is given by
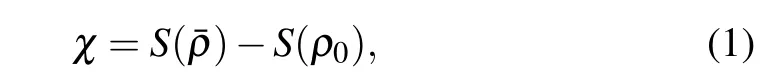
whereρ0is the initial resource state shared between Alice and Bob, ¯ρrepresents the density matrix after quantum dense coding,Sis the von Neumann entropy, andχis the capacity of quantum dense coding. For the density matrixρ0,the von Neumann entropy is written explicitly is expressed asS(ρ0)=−∑Z λZlog2λZ, withλZbeing the eigenvalue of the density matrixρ0. In recent decades, attention has been paid to many scenarios of super dense coding over noiseless channels.[3,4]Barenco and Ekert discussed the maximally entangled state and more general initial state of the two particles as well.[5,6]More general case for higher-dimensional[7]entanglement have been argued, which provides more capacity of quantum dense coding than conventional qubit entanglement. Dense coding for continuous variables has been argued by Braunstein and Kimbl.[8]
In addition, the case of uncorrelated noisy channel (i.e.,memoryless channel) has also been discussed.[9]Because noise exists unavoidably in reality, optical fibers and an unmodulated spin chain[10]are practically applied to such quantum noisy channels which are appropriate for long-and shortdistance quantum communication, respectively. Physically,noise is a process that arises through the interaction with the environment. Mathematically, a noisy quantum channel can be described as a completely positive trace preserving(CPTP)linear mapΛ, acting on the quantum state. For uncorrelated cases (channels and states) where the von Neumann entropy fulfills a specific condition, the superdense coding capacity was derived.
The above studies discussed the sequence of qubits passing through an uncorrelated channel by neglecting the correlations between multiple uses of quantum channels. However,neither the correlation effects of the quantum channel nor the transmission rate raising in quantum channel can be neglected,as it has been practically explored in the solid-state implementation of fiber[11]or quantum hardware that suffers lowfrequency noise.[12]The quantum correlated channels have thus received a lot of attention recently.
In this work, we consider the quantum dense coding in correlated noisy channels. Three common noise sources are taken into account: the amplitude damping channel, phase damping channel,and depolarizing channel. Additionally,we analyze the effects of weak measurement and reversal measurement on the capacity of dense coding. The particular plan without weak measurement or reversal measurement is that the initial state directly passes through the correlated channel and then we make a dense coding. As an improvement in the former, the plan with weak measurement and reversal measurement is“weak measurement+correlated noise channel+reversal measurement+dense coding”.
The rest of this paper is organized as follows. In Section 2,the correlated quantum channel and the quantum dense coding capacity are briefly introdiced. In Section 3, are discussed the influence of correlation strength of the channel and the initial entanglement on the capacity of quantum dense coding for different noisy models. The effects of weak measurement and reversal measurement on capacity are also discussed in this section. Finally, the conclusions are drawn from the present study in Section 4.
2. Correlated quantum channel and optimal dense coding capacity

This means that after the (n−1)-th qubit rotates an angleπaround axiskn−1,then-th qubit implements the same rotation with probabilityµor rotates an angleπaround axisknwith probability(1−µ)pkn. Thus,µ ∈[0,1]can be understood as the degree of classical correlation in the channel.Whenµ=0,the model depicts an uncorrelated channel, while forµ=1,the model depicts a fully correlated channel.

whereEk1k2represents the Kraus operator in uncorrelated noise channel andEkkrefers to that in the correlated noise channel.
Then we introduce the capacity for dense coding. Reference[14]showed that thed2signal state(imax=d2−1)generated by mutually orthogonal unitary transformations with equal probabilities yields a maximum valueχ. The set of mutually orthogonal unitary transformations of dense coding for two qubits are

whereIis the second-order identity matrix andρrepresents the density matrix that needs to make dense coding. For simplicity,we suppose 0→00,1→01,2→10,and 3→11.
3. Capacity in three correlated noise channels
The capacity of dense coding through correlated noisy channel is given by
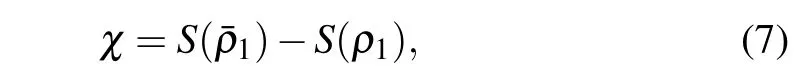
whereρ1is given by Eq. (4) and ¯ρ1is given by Eq. (6). The initial entangled state is changed after having passed through the correlated noisy channel. So the density matrices that we use are different from Eq. (1). Below we mainly discuss the above problems in three common correlated noise channels:amplitude damping channel,phase damping channel,and depolarizing channel.
3.1. Capacity in correlated amplitude damping channel
The amplitude damping(AD)channel can also be used to describe the spontaneous emission of a photon by a two-level atom at low or zero temperature.[15,16]The Kraus operators for one qubit are

while the Kraus operatorsEkkin full-memory amplitude damping channel introduced in Ref.[17],different fromEk1k2are given by

Based on Eq.(6),we can obtain the density matrix of ¯ρ1.Then according to Eq.(7),the capacity of quantum dense coding can be obtained analytically, but it is too long to be written here.By confirming the capacityχ,the influences of the correlation strength of channelµon capacity are depicted in Fig.1. The blue line with empty squares in Fig. 1 corresponds toµ=0,which means that the correlation strength of channel is zero,and what is more, it corresponds to the uncorrelated channel.The purple line with empty circles,the yellow line with empty rhombuses, the green line with empty triangles and the light blue with empty inverted triangles representµ= 0.25, 0.5,0.75, 1, respectively. From this figure, we can reasonably infer that the capacity of quantum dense coding increases monotonically with the increase of correlation strengthµwhen the damping coefficientλof AD channel is fixed. So we can conclude that the correlated channel increases the capacity of quantum dense coding in comparison with the uncorrelated channel.
It is indicated in Ref.[18]that the weak measurement and reversal measurement improve the capacity of dense coding.So we consider the influence of weak measurement on capacity in correlated noise channel.
We know that standard quantum measuring procedure brings an initial state collapse to an eigenstate of the observable. Unlike standard measurement, weak measurement[19]makes so little influence on initial state that almost no initial state collapse happens to its eigenstate. Weak measurement and reversal measurement have been studied theoretically[20]and experimentally.[21]

Fig.1. Variations of capacity of quantum dense coding with damping coefficient λ in correlated amplitude damping channel,where α=β =/2,and blue line with empty squares,purple line with empty circles,yellow line with empty rhombuses, green line with empty triangles, and light blue line with empty inverted triangles correspond to correlation strength of channelµ=0,0.25,0.5,0.75,1,respectively.
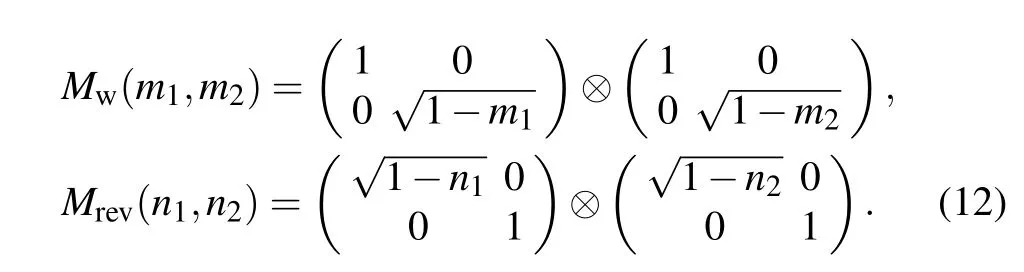
Weak measurement operator and reversal measurement operator for two qubits can be written as Here,Mw(m1,m2) is a weak measurement operator,m1andm2are the weak measurement strengths. In the same presentation,Mrev(n1,n2) is the reversal measurement operator,n1andn2are reversal measurement strengths. For simplicity,we assume thatm1=m2=mandn1=n2=n.
The capacity of quantum dense coding with weak measurement and reversal measurement is

According to Eq.(13),the capacityχof quantum dense coding with weak measurement and reversal measurement is shown in Fig. 2. As for the research of the capacity of quantum dense coding under the influence of weak measurement and reversal measurement, we learn that no matter how the damping coefficientλchanges, the maximum value can be obtained by adjusting the weak measurement strength and reversal measurement strength. For simplicity, assume that the damping coefficientλis a certain value,then we will discuss the effects of weak measurement and reversal measurement. To make it easier to understand,we use a point to analyze. For example,the capacity of quantum dense coding with weak measurement and reversal measurement is 1.7494 for weak measurement strengthm=0.9 and reversal measurement strengthn=0.95 when the damping coefficient of AD channelλ=0.5 and the correlation strength of channelµ=0.5. Meanwhile, the capacity of quantum dense coding without weak measurement or reversal measurement is 0.8842. In this case, the capacity of quantum dense coding under the weak measurement and reversal measurement is greater than that without weak measurement or reversal measurement. Furthermore, the method for weak measurement and reversal measurement can be used for different values of damping coefficientλ,which can make dense coding successful and improve the capacity of dense coding in AD channel.
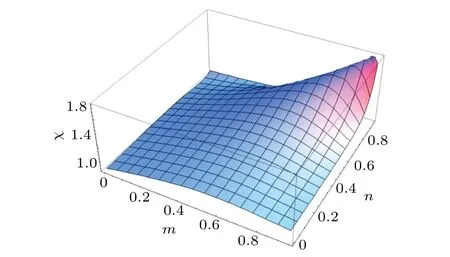
Fig.2.Capacity of quantum dense coding versus weak measurement strength m and reversal measurement strength n,with damping coefficient λ being 0.5,correlation strengthµ being 0.5,and α =β =/2.
3.2. Capacity in correlated phase damping channel

Substituting Eqs. (14) and (15) into Eq. (4), the density matrix elements of the two qubits in the correlated phase damped channel can be expressed in the following form:
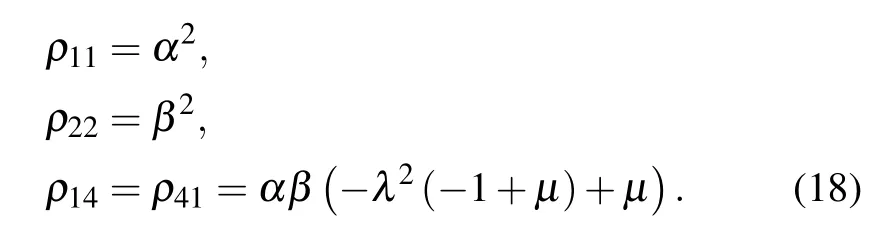
Based on Eq. (7), the capacity of quantum dense coding can be obtained analytically. The influences of the correlation strength of channelµon capacity are depicted in Fig.3. The blue line with empty squares in Fig.3 corresponds to the caseµ=0, which refers to the uncorrelated channel. The purple line with empty circles,the yellow line with empty rhombuses,the green line with empty triangles and the light blue line with empty inverted triangles refers toµ=0.25, 0.5, 0.75, 1, respectively. On the other hand, as discussed in Section 2, the Bell states are eigenstates of the Kraus operators,Eck,in correlated Pauli channel. As a result,they can pass through undisturbed channel via the full-correlated channel.So whenµ=1,i.e.,the channel becomes full-correlated,the capacity of dense codingχis kept at 2. Based on the above discussion,we can reasonably infer that the capacity of quantum dense coding increases monotonically with the correlation strengthµincreasing when the phase damping coefficientλis fixed. So we can conclude that the correlated channel increases the capacity of quantum dense coding in comparison with the uncorrelated channel.

Fig.3. Variations of capacity of quantum dense coding with phase damping coeffciient λ,where α=β =/2. The blue line with solid squares,purple line with empty circles, yellow line with empty rhombuses, green line with empty triangles,and light blue line with empty inverted triangles correspond to the correlation strength of channelµ =0,0.25,0.5,0.75,1,respectively.
We discuss how the weak measurement and reversal measurement affect the capacity of quantum dense coding in phase damped channel as we did in the above section. Besides the normalized factor,the density matrix is
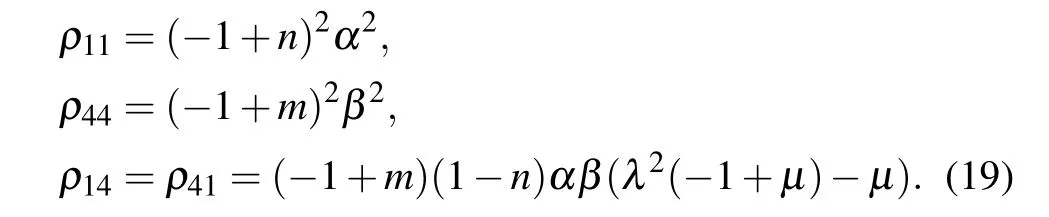
According to Eq.(13),the capacityχof quantum dense coding with weak measurement and reversal measurement can be obtained analytically,but it is too long to be written here. Because the weak measurement strengthm=1 and reversal measurement strengthn=1 is a singular point,we are difficult to find the maximum value of the capacity of quantum dense coding in phase damped channel. For simplicity,we use a point to analyze it. For example,the capacity with weak measurement is larger than that without weak measurement form=0.95 andn=0.95 when the phase damping coefficientλ=0.5 and correlation parameterµ=0.5. But we find the influence of weak measurement and reversal measurement on the capacity to be so weak that it can be neglected.
3.3. Capacity in correlated depolarizing channel

Based on Eq. (7), the capacity of quantum dense coding can be obtained analytically, but the expression is too long to be written here. The influences of the correlation strength of channelµon capacity are depicted in Fig. 4. The blue line in Fig.4 corresponds toµ=0, which corresponds to the uncorrelated channel. The purple line with empty circles, the yellow line with empty rhombuses,the green line with empty triangles,and the light blue line with empty inverted triangles refer toµ=0.25, 0.5, 0.75, 1, respectively. This correlated noise channel also adapts to the situation in Section 2,i.e.,the Bell states are eigenstates of the Kraus operatorsEckin the correlated Pauli channel. As a result, they can pass through the undisturbed channel via the full-correlated channel. So whenµ=1,i.e., the channel becomes full-correlated, the capacity of dense codingχis kept at 2. Like the above part, we can reasonably infer that the capacity of quantum dense coding increases monotonically with correlation strengthµincreasing when the phase damping coefficientλis fixed. So we can conclude that the correlated channel increases the capacity of quantum dense coding in comparison with the uncorrelated channel.
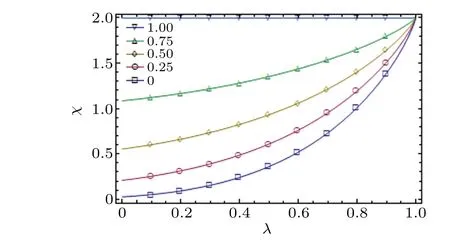
Fig. 4. Variations of capacity of quantum dense coding with depolarizing damping coeffciient λ,where α =β =/2,blue line with empty squares,purple line with empty circles,yellow line with empty rhombuses,green line with empty triangles,and light blue line with empty inversed triangle correspond to the correlation strength of channel µ =0,0.25,0.5,0.75,1,respectively.
Then we discuss the influence of weak measurement and reversal measurement on the capacity.
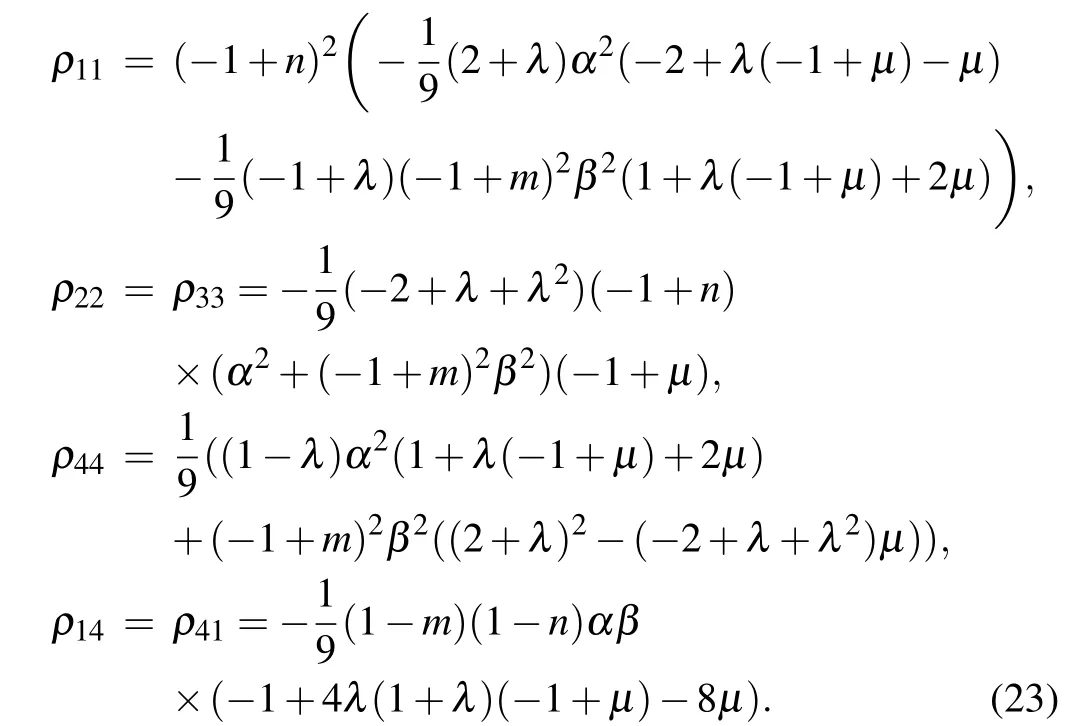
We find that the capacity with weak measurement is larger than without weak measurement form=0.99 andn=0.99 when the depolarizing damping coefficientλ=0.5 and correlation strengthµ=0.5. But the influence of weak measurement and reversal measurement on the capacity is very weak, specifically on the order of 10−2.
4. Conclusions
In this paper,we studied the dense coding capacity in correlated noise channels and the influence of weak measurement and reversal measurement on the capacity. We find two conclusions: the first one is that the correlated noisy channel can improve the capacity of dense coding in comparison with uncorrelated noisy channel. It is easy to understand in physics.The correlated noisy channel is the situation where time correlations cannot be neglected. It means that two qubits are sent almost at the same time, and the channel properties will be unchanged. But time lapse is larger in uncorrelated noisy channel. So the capacity of the correlated noisy channel is larger than that of uncorrelated noisy channel. The second conclusion is that the weak measurement and reversal measurement can further improve the capacity of dense coding in correlated amplitude damping channel, but this improvement is very small in correlated phase damping channel and correlated depolarizing channel. The explanations about this are correlated with the amplitude damping channel that is non-Pauli channel,but correlated phase damping channel and correlated depolarizing channel are Pauli channel,so the improvements by weak measurement and reversal measurement are different.
- Chinese Physics B的其它文章
- Erratum to“Floquet bands and photon-induced topological edge states of graphene nanoribbons”
- Viewing the noise propagation mechanism in a unidirectional transition cascade from the perspective of stability*
- Nonlinear signal transduction network with multistate*
- Optical strong coupling in hybrid metal-graphene metamaterial for terahertz sensing*
- Any-polar resistive switching behavior in Ti-intercalated Pt/Ti/HfO2/Ti/Pt device*
- Magnetic two-dimensional van der Waals materials for spintronic devices*

