Viewing the noise propagation mechanism in a unidirectional transition cascade from the perspective of stability*

Qi-Ming Pei(裴启明), Bin-Qian Zhou(周彬倩), Yi-Fan Zhou(周祎凡),Charles Omotomide Apata, and Long Jiang(蒋龙)

School of Physics and Optoelectronic Engineering,Yangtze University,Jingzhou 434023,China

Keywords: noise,noise propagation,stability,linear approximation

1. Introduction

Noise is unavoidable and permeates into all levels of biological systems.[1-3]It includes intrinsic noise generated by random biochemical reactions and external noise arising from changes in the microenvironment.

Noise plays a constructive role in key cellular activities.It is beneficial to metabolism, development, the cell cycle,circadian rhythms, aging, and so on.[4,5]The noised-induced stochastic alternation between the focus and the limit cycle will result in a synchronized early after-depolarization-like rhythm.[6]Driven by noise,some spatiotemporal dynamic behavior (such as synchronization, spiral waves, spatial periodicity, and time sequences) will appear, thereby affecting the brain’s function.[7]

Recent studies have shown that noise is also important in the propagation of neuroelectric signals.[8-11]In the functional neural circuit that combines a thermistor and a phototube, it is possible to detect coherent resonance by applying Gaussian white noise.[12]The direct delayed feedback control through noise can effectively suppress the beta oscillation in the Parkinson state.[13]From a physical point of view, noise driving will inject energy.[14]Energy can be encoded to adjust the dynamics of nonlinear oscillators and circuits,and can especially cause non-coupling synchronization.[15]In two nonlinear circuits,encoded energy can enhance the dependence of synchronization and dynamics on the initial values.[16,17]

In other cases,noise is deleterious and hence needs to be suppressed.[18]It can reduce biological fitness and cause genetic mutations.[19]In tumor cells,when noise is too large,the instantaneous cell number will greatly deviate from the equilibrium state,which is a potential risk for tumors.

It was confirmed that noise can be propagated.As early as 2005,the propagation of noise in gene networks was observed by measuring the correlation between gene expressions in a single cell.[20]In the process of signal transduction,noise can also propagate with the signal and seriously affect the fitting response.[21]Furthermore, research in 2018 showed that the expression noise coming from one gene can propagate to the growth,metabolism,and expression of all other genes.[22]At the cellular level, noise can propagate from upstream cells to downstream cells in the colonic cells cascade, and the transmitted noise has an important influence on the total noise in downstream cells.[23,24]

Stability analysis is another key issue in the fields of systems, control, and signal processing.[25]It is an important tool for studying the dynamic behavior of nonlinear systems. In the mathematical model of physical processes, only its stable solutions correspond to the motions that are observed in nature.[26]The high stability of physical properties of the equipment is the goal we have been pursuing, such as thinfilm photonic devices,[27]optical atomic clocks,[28]and perovskite thermoelectric devices.[29]However, sometimes instability is also very important. For example, the nonlinear growth of hydrodynamic instabilities will lead to the degradation of inertial confinement fusion implosion.[30]The instability of Richtmyer-Meshkov is a key factor in the rupture and atomization of liquid films caused by shock waves.[31]

Recently,stability analysis has become a hot and promising research topic.[32]It can provide some suggestions not only for the control of rumor propagation or virus transmission,but also for the clinical treatment of diseases. For example, stability analysis of a SAIR rumor-spreading model was used to discuss the optimal control strategy for reducing the frequency of rumor propagation.[33]Stability analysis and numerical simulation of the SEIR model on COVID-19 transmission provided some references for early prevention of the spread of COVID-19 in Indonesia.[34]Through stability analysis of a fractional HIV-AIDS epidemic model with memory and general incidence rate,an optimal strategy to minimize the spread of the disease in the population can be determined.[35]Stability analysis and numerical simulation of a HPV infection model with early-stage cervical cancer showed that the optimal control of HPV infection can reduce the resulting cancer cells.[36]

Then, interesting questions arise. For a unidirectional phenotypic transition cascade, how does one study the noise properties while maintaining a steady equilibrium state? What is the mechanism of noise propagation from the perspective of stability? To address these issues, we choose a threecompartment model of a colonic crypt[37,38]as an example of a stochastic computation system. Instead of the nonlinear dynamic evolution method[39,40]and the linear stability analysis method,[41]the analytical solution of the Langevin equation with elasticity factors[42-44]is used for discussion. From the normalized fluctuation-dissipation relationship, noise propagation formulas are obtained. Through the simulation of these theoretical formulas, the noise propagation mechanism from the stability viewpoint is studied.

In our work,all data are compared with those of the Gillespie algorithm,[45,46]which is a classic approach for stochastic simulation of chemical systems.[47]It is usually used to test whether theoretical results are correct,because this algorithm can give statistically accurate simulations.

This paper is organized as follows. In Section 2,a phenotypic transition cascade in a colonic crypt with coupled saturation and linear feedback is constructed. In Section 3, theoretical formulas with an elasticity factor for noise propagation are derived. The influence of the stability factor of cell equilibrium on noise and noise propagation is studied in Section 4.We end with conclusions and discussions in Section 5.

2. Transition cascade in a colonic crypt with coupled saturation and linear feedbacks

2.1. Model

In the three-compartment model of a colonic crypt,[37]stem cells (SCs) are the source and can differentiate into transit-amplifying cells (TACs), and then TACs can continuously differentiate into fully differentiated cells(FDCs),while two differentiates are irreversible, as shown in Fig. 1. The differentiation probability from SCs to TACs per unit time isα12, and that from TACs to FDCs isα23. SCs and TACs can self-proliferate,and the self-proliferation probabilities per unit time area1anda2, respectively. FDCs can neither selfproliferate nor differentiate. The three compartments can experience procedural death and be removed from the crypt.The corresponding probabilities per unit time areb1,b2,andb3,respectively.

Fig.1.A schematic diagram of the three compartments in a colonic crypt,[37]in which SCs can differentiate into TACs and TACs can differentiate into FDCs. Here,a1 and a2 are the self-proliferation probabilities per unit time of SCs and TACs,respectively,while b1,b2,and b3 are the programmed death probabilities per unit time of each compartment. Here, α12 and α23 are the differentiation probabilities per unit time from SCs to TACs,and from TACs to FDCs, respectively. To maintain cell populations in homeostasis, α12 is regulated by saturation feedback;α23 is regulated by linear feedback.

TakingNi(i= 1, 2, 3) as the numbers of SCs, TACs,and FDCs,respectively,the time evolution equation of the cell populations is

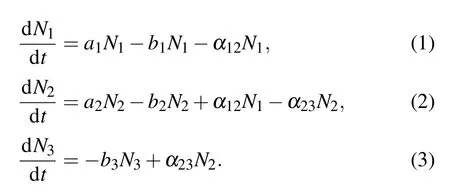
If all the reaction probabilities are constant,then the three cells will either die instantly or grow to infinity immediately,neither of which conforms to the normal human physiological state.To keep cell populations in homeostasis, linear feedback and saturation feedback were introduced to regulate the differentiation rate.[46]In linear feedback,the cell differentiation rate increases linearly with the increase in its population,and there is no upper limit. Linear feedback is strong enough to prevent any unlimited growth of three cell populations. In saturation feedback,although the differentiation rate also increases with the increase in its population,it will reach a maximum instead of increasing indefinitely. Saturation feedback can help explain the presence of benign tumors or adenomas before carcinogenesis occurs. Rather than a single and identical feedback, the coupled saturation and linear feedbacks are considered in this paper:that is,the differentiation rate of SCs is regulated by saturation feedback, and that of TACs is regulated by linear feedback. Thus,α12=α10+(k1N1)/(1+m1N1),α23=α20+k2N2,in whichα10andα20are an inherent differentiation rate of SCs and TACs, respectively. Here,ki(i=1,2)represents the speed of the feedback response,andm1represents the feedback saturation of SCs. Some studies have shown that this coupled feedback is more suitable for explaining tumor development.

2.2. Steady states

2.3. The elasticity

To qualitatively describe how phenotypekaffects the balance between elimination and production of phenotypei, the elasticityHki(i,k=1, 2, 3) is introduced, which is defined as[42]

It can be seen thatH11,H22>0 andH12,H23<0 because〈Ni〉and the parameters are all positive. So,for SCs and TACs,the impact on their self-elimination is greater than that on their self-production. And upstream cells have a greater influence on the production of downstream cells than on their elimination. This is because,regardless of whether linear feedback or saturated feedback acts on cell differentiation,it can promote their own elimination, thereby generating more downstream cells.

In this sense, the elasticityHkican be understood as the regulation intensity.

2.4. Langevin equation

Solving Eq.(13),we can get

As the source of the cascade,SCs will not be affected by downstream cells,so its stability equilibrium condition is only determined byH11.Because downstream cells will be affected by upstream cells, their stability conditions are related to upstream cells. For example,bothH22andH12jointly determine the stability conditions of TACs’equilibrium,andH33andH23together determine the stability conditions of FDCs’ equilibrium,see Eq.(15). WhenH1=H11>0,H2=H22+H12>0,andH3=H33+H23>0,SCs,TACs and FDCs are in a stable equilibrium state, respectively. Otherwise, they will be in an unstable equilibrium state: that is, once SCs, TACs, or FDCs are disturbed,they will be far from the equilibrium state.

In this sense,the total regulation intensityHican also be interpreted as a stability factor of cell equilibrium, which is used to judge whether the cell can return to its original equilibrium state after being disturbed.

3. Noise propagation formulas

In stochastic dynamics theory, the master equation gives the joint probability distribution of population dynamics.[49]Although the master equation cannot be solved, it can be expanded using van Kampen’s Ω-expansion method to obtain the linear Fokker-Planck equation.[50]In the steady state,the coefficients of the Fokker-Planck equation will satisfy the fluctuation-dissipation relationship. To facilitate discussion, the fluctuation-dissipation relationship should be normalized[23,24]to

Vincludes normalized varianceViiand normalized covarianceVik(k ̸=i). The former characterizes the fluctuation in phenotypei,and the latter represents the degree of correlation between the noise in phenotypeiand that in phenotypek.

By expanding Eq.(17)withVi j=Vji(j ̸=i),we can getVi jas follows:

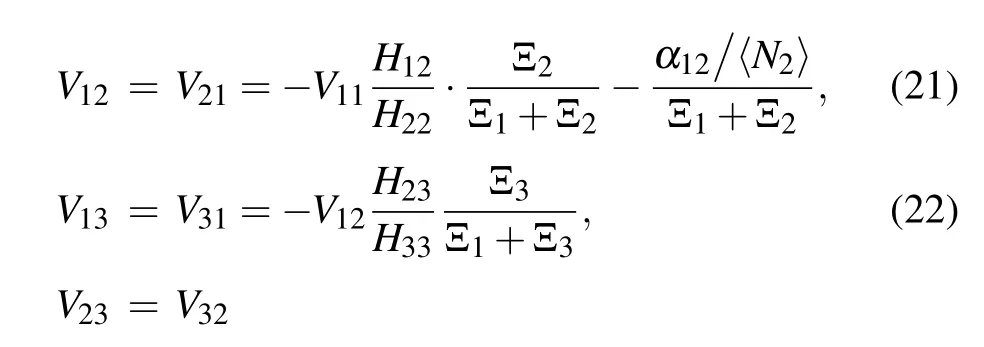
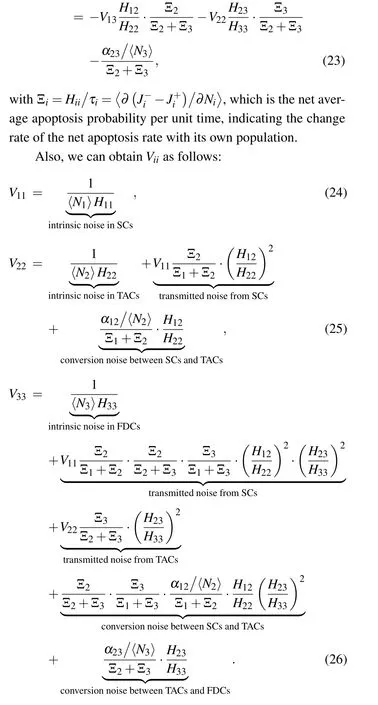
The normalized variationViidescribes the total noise in phenotypici. The noise decomposition method here is consistent with that in the gene network.[43]The intrinsic noise originates from a small number of cells, transmitted noise is caused by the total noise of upstream cells, and inter-conversion noise comes from the interaction(i.e.,differentiation)of cells.

大港油田在开发过程中聚焦突出问题，抓住主要矛盾，以创新为引领，突出理论与实践的结合，开发“五场”建设取得了很好成果。开发指标上，油田整体的自然递减由19%下降至15.8%，含水上升率由0.5 下降至-0.3，采收率整体提高了3 个百分点，相当于增加了1800 万吨可采储量。效益指标上，油田开发完全成本下降了16.1%，实现了低油价下盈利，生产综合能耗由93.8 千克标煤/吨下降到88.2 千克标煤/吨。劳动效率上，一线劳动用工总量下降了5%，公司总体用工结构更加优化。大港油田的开发“五场”建设实践，值得我国东部老油田借鉴。

SCs are the sources of this phenotypic transition cascade;they do not have an external fluctuation environment coming from other phenotypes. Therefore,there is only intrinsic noise in SCs,see Eq.(24).In downstream cells,in addition to the intrinsic noise,transmitted noise will be generated due to the external fluctuation environment provided by the upstream cell.Due to the differentiation from upstream cells, there is also inter-conversion noise,see Eqs.(25)and(26). Intrinsic noise is inversely proportional to the product of its average〈Ni〉and self-elasticityHii. The transmitted noise depends on the total noise of upstream phenotypesVii, the elasticityHki, and the net average apoptosis probability Ξi. The inter-conversion noise is determined by the differentiation rateαi,i+1(i=1,2),Hki,and Ξi. From Eq.(26),we also find the noise in SCs can propagate to FDCs,even if SCs cannot directly differentiate to FDCs. Moreover,the noise in the downstream phenotype can be expressed as a linear function of the noise in the upstream phenotypes. That is,the contribution of upstream phenotypic fluctuations to downstream phenotypic fluctuations is additive.

4. Simulations and results

4.1. The characteristics of the stability factor

From Eq. (4), we find that both the inherent net growth rate of SCsη1and the feedback response speedk1determine the steady state of SCsNs1, thereby affecting the other two steady states. Moreover,η1is the key parameter.[37]So, we chooseη1as the control variable. Anda1will vary withη1due toa1=η1+b1+α10. The other parameters area2=0.5,b1=0.1,b2=0.1,b3=0.323,α10=0.1,α20=0.2,k1=0.1,m1=0.1,andk2=0.01.[32,33]In this paper,the dimensionless parameters are used.

The steady statesNsias a function ofη1are given in Fig.2.Herein,η1changes in the range[0.3,1]. It is found that whenη1<0.8, the steady states of three populations increase approximately linearly with the increase inη1, and the changes are relatively gentle. Onceη1>0.8,they will increase rapidly and quickly reach infinity. FDCs increase the fastest,followed by SCs,and TACs increase the slowest.

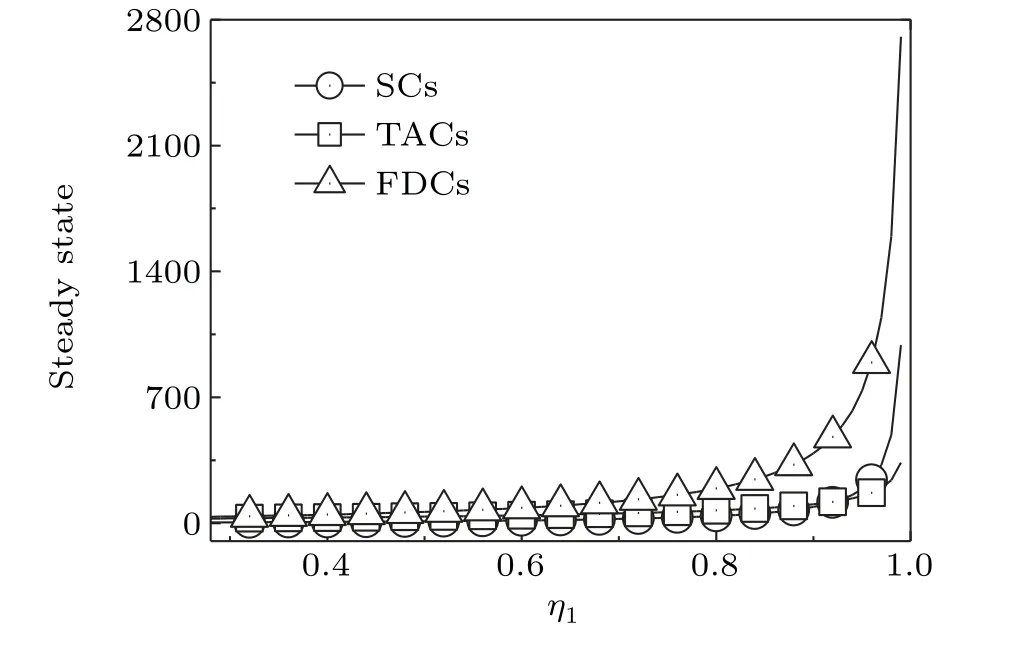
Fig.2. Steady states Nsi (i=1,2,3)versus SCs inherent net growth rate η1.The lines are theoretical predictions according to Eq. (4). Other parameter values are given in the text. All the parameters are measured in hour−1.

In the mean field theory,the mean value can be replaced by its stationary population number, namely〈Ni〉=Nsi. According to Eqs. (7)-(12),Hias a function ofη1are given in Fig.3.

It can be seen thatH1>0 andH2>0,then SCs and TACs are in a stable equilibrium state.In other words,due to the disturbanceξ1(t)orξ2(t),even if SCs or TACs deviate from the equilibrium state instantaneously,they will return to the original state. However,H3<0,that is,FDCs are in an unstable equilibrium state. Therefore,in colonic crypts,FDCs are most likely to induce colon cancer. Once FDCs are disturbed,they will quickly grow to infinity.

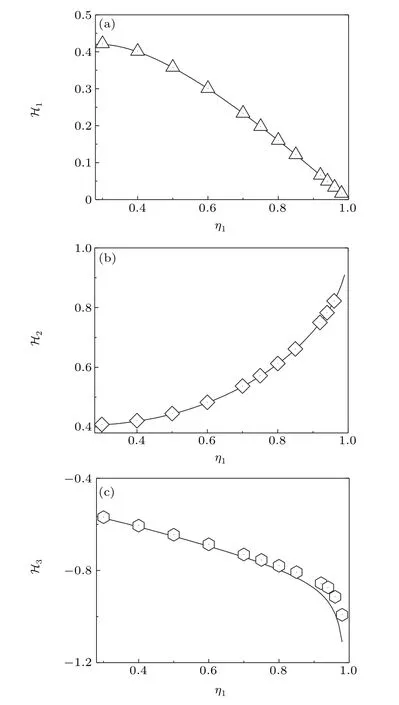
Fig. 3. The stability factor ℋi (i=1, 2, 3) versus SCs inherent net growth rate η1.The lines are theoretical predictions according to Eqs.(7)-(12). Hollow markers are from simulations using the Gillespie method.[45,46] Other parameter values are given in the text. All the parameters are measured in hour−1.

From Fig.3(a),we findH1will decrease with the increase inη1. So,the larger the parameterη1,the smaller the regulation intensityH1, and the more difficult it will be to control the stability of SCs. In contrast,H2will increase with the increase inη1, see Fig. 3(b). Then, the larger the parameterη1,the larger the regulation intensityH2,and the easier it will be to control the stability of TACs. From Fig.3(c),it can be found thatH3will also decrease with the increase inη1,

whereas,H3<0; therefore, the larger the parameterη1, the smaller the regulation intensityH3,and the greater the degree of instability of the FDCs’equilibrium.

In short,whenH1,H2,andH3are large,the homeostasis among the three cells is easy to maintain,see Table 1.

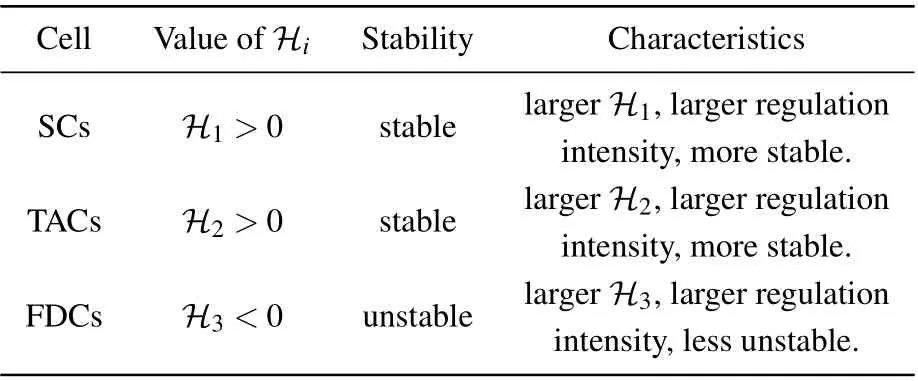
Table 1. The stability characteristics of the three cells.

4.2. Effects of the stability factor on the normalized covariance

It is shown thatV12,V23,V13>0. Therefore, any two fluctuations in the three cell populations are positively correlated. In colon cells, downstream cells are mainly produced by the differentiation of upstream cells, so downstream cells will change synchronously with upstream cells. In addition,although there is no direct interaction between SCs and FDCs,the correlation between the two fluctuations of SCs and FDCs is positive. That is, the correlation can be transmitted from SCs to FDCs through TACs. Moreover,V13has an effect on the correlation between TACs and FDCsV23,see Eq.(23).

By comparing the upper layer figures, we find that the covarianceV12is a monotonically increasing function of the stability factorH1orH3, whereas, it is a monotonically decreasing function ofH2. So,the correlation between SCs and TACs will be strengthened with the increase inH1orH3,and it will be weakened with the increase inH2.

The middle and bottom layer figures show that all curves ofV23andV13are asymmetric parabolas opening upwards.Therefore, for some optimal total regulation intensities, there is always a minimum value forV23andV13.

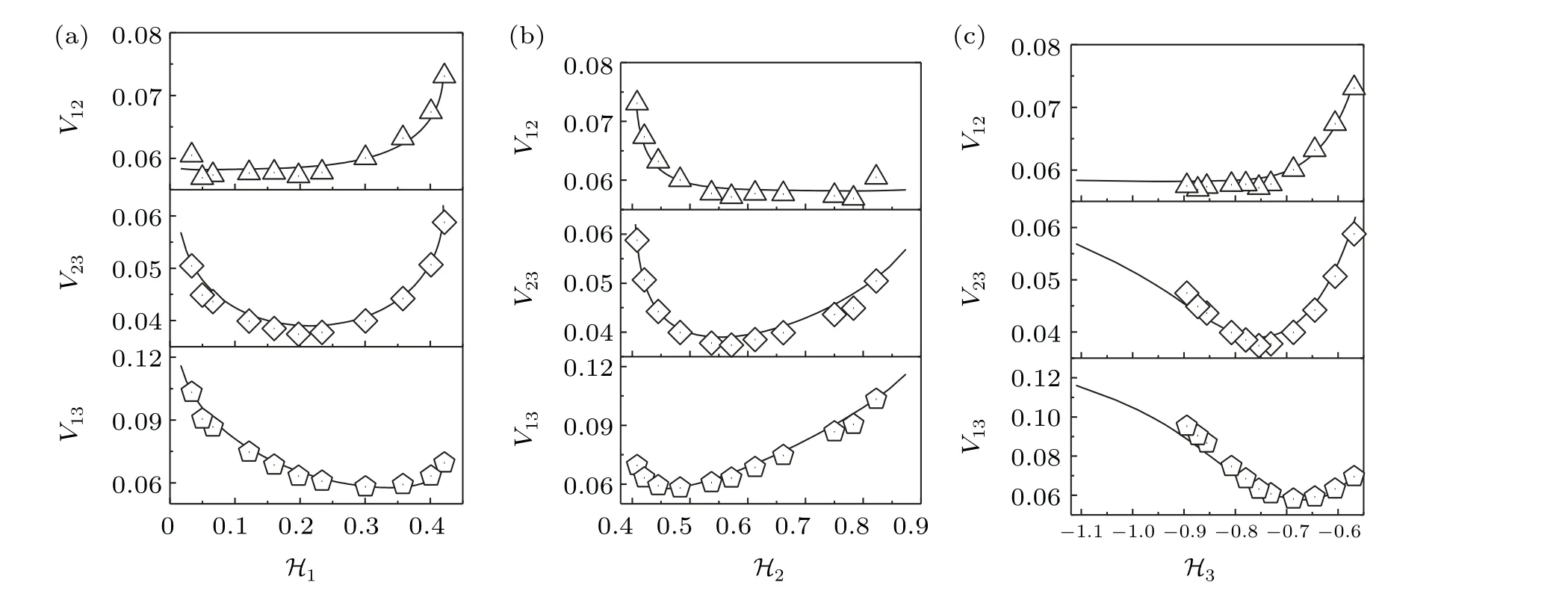
Fig. 4. Normalized covariance Vij =Vji (i,j =1,2,3; j ̸=i) versus the stability factor ℋi. The lines are theoretical predictions according to Eqs. (21)-(23). The hollow markers are from simulations using the Gillespie method.[45,46] Other parameter values are given in the text. All the parameters are measured in hour−1.

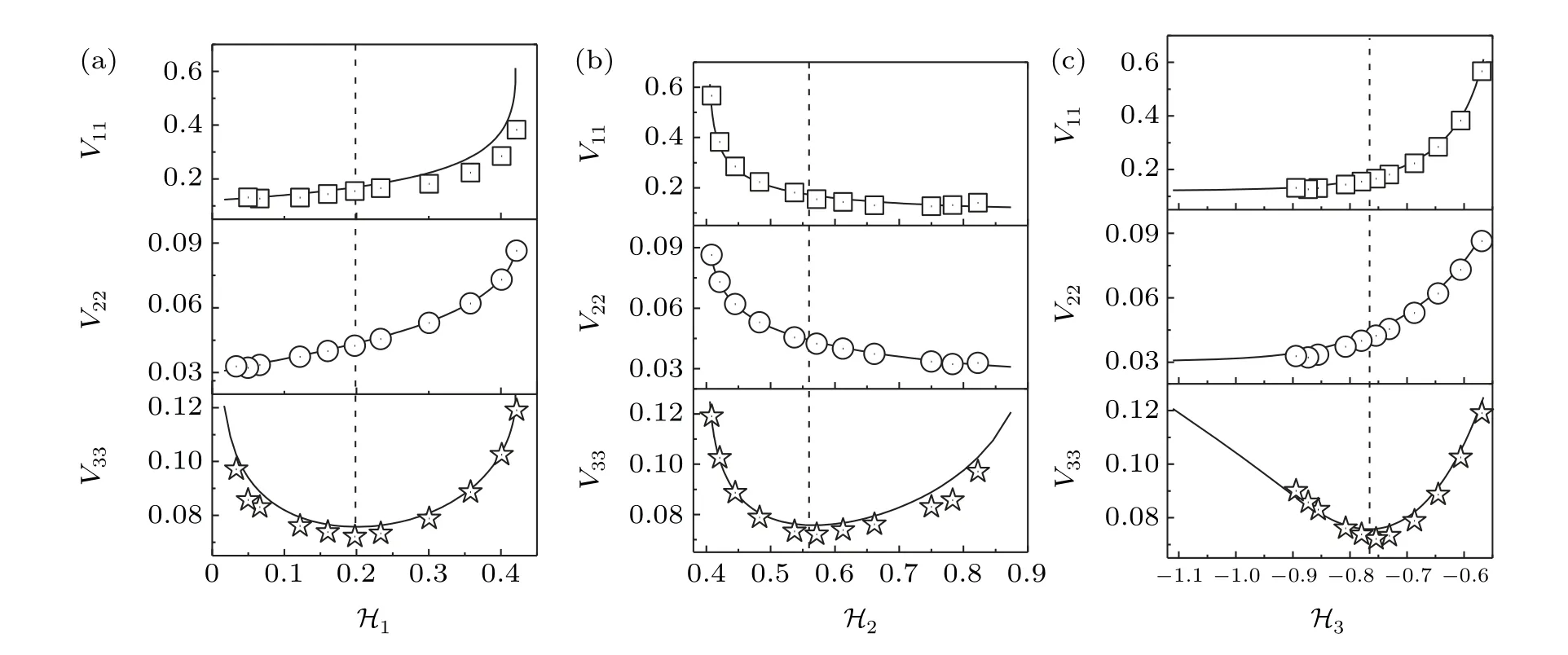
Fig.5.Noise Vii(i=1,2,3)versus the stability factor ℋi.Solid lines are theoretical predictions according to Eqs.(24)-(26).The hollow markers are from simulations using the Gillespie method.[45,46] Dashed lines are auxiliary lines. Other parameter values are given in the text. All the parameters are measured in hour−1.

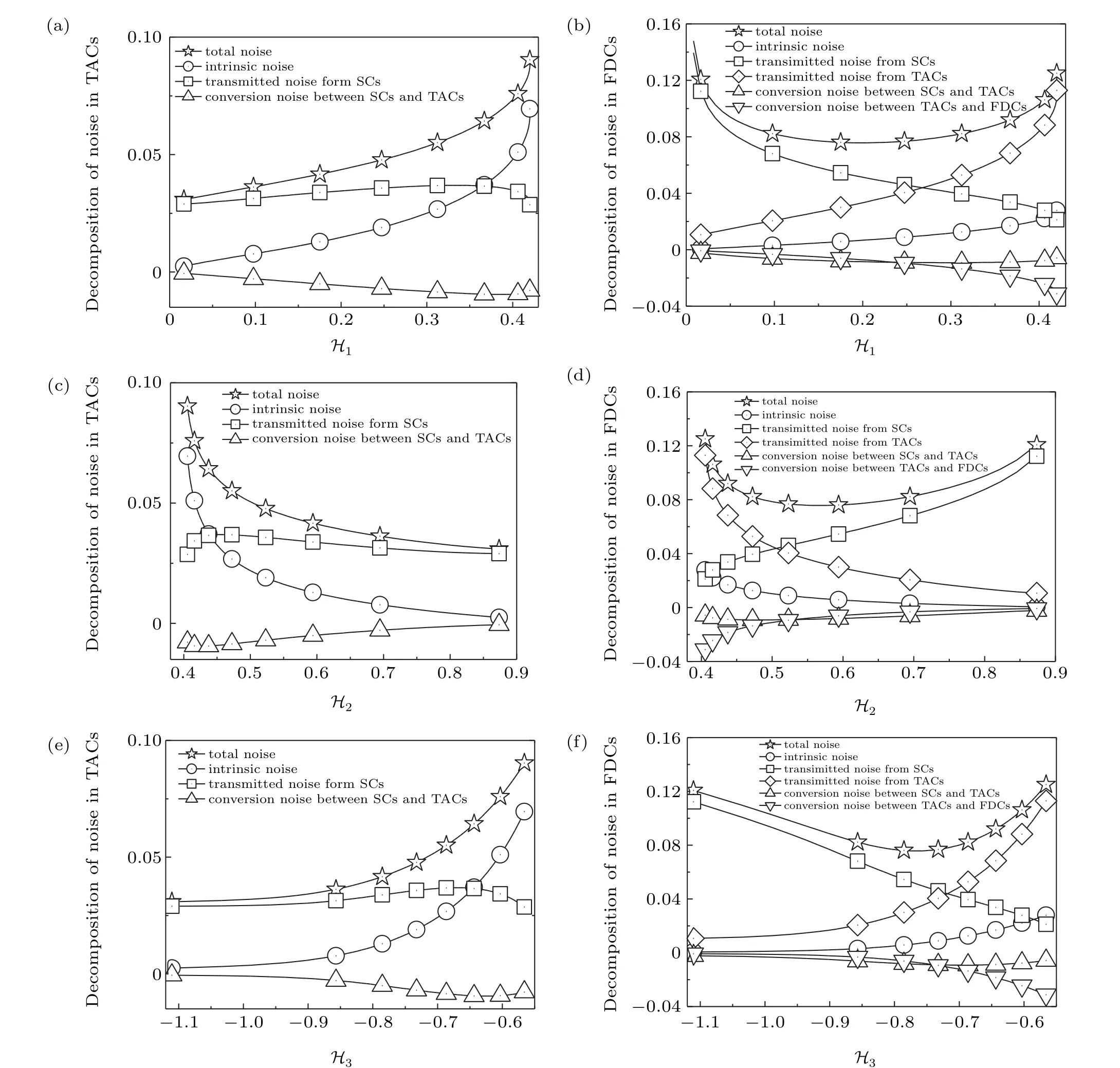
Fig. 6. Noise decomposition versus the stability factor ℋi. The lines are theoretical predictions according to Eqs. (25)-(26). Other parameter values are given in the text. All the parameters are measured in hour−1.

4.3. Effects of the stability factor on the noise

By using Eqs. (24)-(26), we can get the effects of the stability factorHion the noiseVii(i=1, 2, 3), as shown in Fig.5. All analytical predictions are in accord with numerical simulations by the Gillespie stochastic algorithm.

It is found that bothV11andV22are monotonically increasing functions of regulation intensityH1andH3,and they are monotonically decreasing functions ofH2. Thus,with the increase inH1orH3, the total noise in SCs and in TACs will increase,and with the increase inH2,they will decrease.The curves ofV33are asymmetric parabolas opening upwards.Therefore, the total noise in FDCs always has a minimum value for some optimal regulation intensities.

From Table 1, we can see that largerH1andH3values help maintain cell equilibrium. However,the larger values ofH1andH3will cause the total noise in TACsV22to be very large, see the middle layers in Figs. 5(a) and 5(c). Then, the instantaneous number of TACs will be much larger than its equilibrium number, which may induce colon cancer. Therefore, to meet the high stability and low noise requirements of TACs,H1andH3should take intermediate values. ForH2,its smaller value will not only cause larger noise in TACsV22,but also reduce the cell’s stability;see the middle layer in Fig.5(b). So,a slightly largerH2value will be beneficial.

For anyHi, there is an intermediate value (indicated by the dashed line)to minimize the total noise of FDCsV33; see the three lower layers in Fig. 5. By comparingV11,V22, andV33in the same figure, we find that the intermediate value ofHi(indicated by the dashed line) may also meet the requirements for the high stability and low noise of TACs. Therefore,the value ofHicorresponding to the minimum noise in FDCs may be the best choice to enable colon cells to maintain the high stability and low noise of the cascade.

4.4. Effects of the stability factor on the noise propagation

According to Eq.(25),the total noise in TACs can be decomposed into three parts: the intrinsic noise,the transmitted noise from SCs, and the inter-conversion noise between SCs and TACs, as shown in Figs. 6(a), 6(c), and 6(e). According to Eq. (26), the total noise in FDCs can be decomposed into five parts: the intrinsic noise, the transmitted noise from TACs, the transmitted noise from SCs, the inter-conversion noise between TACs and FDCs,and the inter-conversion noise between SCs and TACs,as shown in Figs.6(b),6(d),and 6(f).All analytical predictions are in accord with numerical simulations by the Gillespie stochastic algorithm.

From the three figures on the left,we find the conversion noise between SCs and TACs is relatively small and can be omitted. The total noise in TACsV22is mainly determined by its intrinsic noise and the transmitted noise from SCs.With the increase inHi, the change in the transmitted noise from SCs is relatively small. Then,the change inV22is consistent with that of the inherent noise.

From the three figures on the right, we find the intrinsic noise and the two conversion noises are relatively small and can be omitted. The total noise in FDCsV33is mainly determined by two transmitted noises from TACs and SCs. With the increase inH1andH3,the transmitted noise from SCs is decreasing, and the transmitted noise from TACs is increasing, resulting in the total noise in FDCs first decreasing and then increasing. In contrast,with the increase inH2,the transmitted noise from SCs is increasing,and the transmitted noise from TACs is decreasing, also resulting in the total noise in FDCs decreasing first and then increasing.

Shortly, the total noise in the source cell only includes intrinsic noise. For the downstream cell, if it can proliferate itself, the total noise is mainly determined by its intrinsic noise and the transmitted noise from upstream cells, and its intrinsic noise is dominant;if it cannot self-proliferate,the total noise is mainly determined by transmitted noises from upstream cells, and with the stability factor increasing, one transmitted noise increases and the other decreases, resulting in a minimum value of the total noise.

5. Discussion and conclusions

Noise is inevitable and plays a constructive role in various biological processes. Whether it is at the gene level or at the cell level,the propagation of noise is confirmed. Maintaining the stability of cell population homeostasis is another key issue.

In a unidirectional phenotypic transition cascade of colonic cells, there are three compartments: SCs, TACs, and FDCs. SCs can differentiate into TACs, and their differentiation rate is regulated by saturated feedback; TACs can differentiate into FDCs,and their differentiation rate is regulated by linear feedback.

The stability factor is introduced into the colon cells cascade, and the influence of the stability factor on noise propagation is studied according to the noise propagation formulas.It is found that the value of the stability factor corresponding to the minimum noise in FDCs may be the optimal choice to enable colonic cells to keep the high stability and low noise of the cascade. Moreover, the total noise in the source cell only includes intrinsic noise. For the downstream cell,if it can proliferate itself,the total noise is mainly determined by its intrinsic noise and the transmitted noise from upstream cells,and its intrinsic noise is dominant;if it cannot self-proliferate,the total noise is mainly determined by transmitted noises from upstream cells, and with the stability factor increasing, one transmitted noise increases and the other decreases, resulting in a minimum value of the total noise.

All analytical predictions in this work are consistent with the numerical simulations by the Gillespie stochastic algorithm.[45,46]It is difficult to quantitatively compare our theoretical results with biological experiments or medical clinical observations, because we only found a small amount of experimental data involving the number of SCs in vivo. Moreover,different experimental groups use different experimental protocols,so the number of SCs obtained is also different. In addition,we have not found real data on the number of TACs and FDCs in published papers up to now.

Noise propagation in colon cells has been studied in our two recent papers. In Ref.[24],pure saturation feedback was used to regulate colon cell differentiation.Taking the upstream cells as input signals and the downstream cells as output signals,noisy signal propagation and amplification were studied.In Ref.[51],four coupled feedbacks were considered to compare the impacts of different feedbacks on noise and noise propagation of cells. The above works only focused on the noise propagation,but ignored the stability of cell population homeostasis. In this paper, we considered the coupled saturation and linear feedbacks to regulate colon cell differentiation,which is more suitable for explaining tumor development.Based on the stability factor, the characteristics of noise and noise propagation were studied, and the mechanism of noise propagation was analyzed. The results obtained are valuable.

This work applies both stochastic dynamics theory and nonlinear dynamics theory to the study of the noise propagation mechanism,which will provide a new theoretical idea for maintaining the homeostasis of cells in living systems,thereby preventing tumor growth. However,we only considered saturation feedback and linear feedback because, so far, we have not found other feedback that can maintain colon cell homeostasis.Although the form of noise decomposition is the same,different feedbacks will directly affect the value of the stability factor, thereby affecting the characteristics of total noise.Finding other feedback to study the mechanism of noise propagation will be one aspect of our future work. In addition,this transitional cascade of colon cells contains only three phenotypes, and it is unidirectional. If there are more phenotypes in the cascade or the transition between cells is bidirectional,what will happen? This will be another aspect of our future work,and there may be many interesting results.