一种半球谐振子性能参数辨识算法

林志辉, 周 斌, 张文明, 张 嵘

(1.清华大学 精密仪器系导航技术工程中心, 北京 100084;2.中国人民解放军陆军军事交通学院 镇江校区,江苏 镇江 212003)

0 引言

半球谐振陀螺具有精度高,寿命长,体积小,结构简单等突出优点,在武器制导、舰艇导航及飞行器导航等方面具有广阔的应用前景[1]。

半球谐振陀螺的精度与谐振子的频差、频率主轴、阻尼差、阻尼主轴和品质因数(Q)值等性能参数有关[2]。精确地辨识这些参数,既是准确评价谐振子性能的关键,也是离子束修调工艺消除频差和阻尼差,提升谐振子性能的前提。

李绍良等[3-4]提出了一种基于幅频响应特性的频差和频率主轴辨识方法,以及一种根据振动信号包络周期辨识频差方法。卢宁等[5]提出了一种通过反复调整激励位置寻找频率主轴,并根据2个频率主轴位置的自由振动信号相位差辨识频差的方法。袁立山等[6]提出了一种在相隔 22.5°的两个位置上分别进行激励,根据自由振动过程中各自节点的振幅比值辨识频率主轴的方法。魏振楠等[7-8]提出了一种基于包络拟合的辨识方法,可以同时测量品质因数、频差和频率主轴。这些方法在原理上忽略了阻尼差的影响,无法辨识阻尼差和阻尼主轴,而且当频差与阻尼差的数值大小相当时,这些方法将失效。

本文通过分析基于自由振动方程和基于解调量动力学方程的2种辨识方法的不足,提出一种基于二次型变量E、H、R、S动力学方程的性能参数辨识方法,并进行了数值仿真和实验验证。

1 辨识算法原理

1.1 辨识方案分析

1.1.1 自由振动方程

半球谐振子的自由振动方程为

(1)

式中:τ0为平均衰减时间常数;Δ(1/τ)为阻尼差;θτ为阻尼主轴;γ为角度增益系数;Ω为角速度;ω0为固有频率;Δω为频差;θω为频率主轴。

根据自由振动过程中x、y通道的采样数据,直接基于式(1)用最小二乘法可辨识阻尼矩阵D和刚度矩阵K,进而计算出Δω、θω、Δ(1/τ)、θτ等参数。

直接基于式(1)进行辨识存在以下缺点:

1) 数值计算误差大。高性能谐振子阻尼矩阵的数值在10-3量级,刚度矩阵在109量级,Δω和Δ(1/τ)在10-4量级,数值量级相差大,容易引起较大的数值计算误差。

2) 数据量和计算量大。谐振子频率通常在3～10 kHz,采集振动数据需要较高的采样率,而待辨识的参数量级小,辨识需要较长时间的测试数据,导致数据量和计算量较大。

3) 辨识精度易受温度变化影响。常温下,石英玻璃的杨氏模量温度系数约为180×10-6,温度变化1 K,刚度矩阵的数值变化在105量级,远大于待辨识参数,易引起较大的辨识误差。

1.1.2 解调量动力学方程

使用角频率为ωr(接近ω0)的正弦和余弦参考信号对x,y进行同步解调,得到4个解调量(xc、yc、xs、ys)。解调量与振动信号有如下关系:

(2)

采用平均法可建立解调量的动力学方程:

(3)

其中:

(4)

利用最小二乘法辨识矩阵D和W,可以计算出待辨识参数Δω、θω、Δ(1/τ)、θτ。解调量是慢变量,且D和W的数值量级相近,这种方法可以有效地降低计算量和数值计算误差,但不足之处在于辨识精度容易受温度变化影响。矩阵W与ω0有关,温度变化1 K,ω0数值变化量远大于待辨识参数。

1.1.3 二次型变量E、H、R、S动力学方程

采用二次型变量E、H、R、S作为观测变量:

(5)

对式(5)求导,并将式(3)代入计算,整理后可得:

(6)

其中:

(7)

da=4γΩ

(8)

(9)

(10)

wc=Δωcos(4θω)

(11)

ws=Δωsin(4θω)

(12)

式(7)～(12)与固有频率ω0无关,对温度变化不敏感。本文基于此方程提出辨识算法。

1.2 辨识算法

对式(6)两端进行积分,将微分方程转换成代数方程,得到:

(13)

其中:

(14)

(15)

(16)

(17)

在每个采样时刻,根据式(13)可得到4个方程。联立这些方程,使用线性最小二乘法可计算出方程参数,进而可根据方程参数计算出待辨识参数:

(18)

(19)

(20)

(21)

(22)

对于高Q值、小频差谐振子,式(13)中的参数很小,自由振动过程中E、H、R、S变化缓慢。如果谐振子对称性较高,dc、ds、wc、ws≪d0,自由振动过程中E、H、R、S将近似等比例衰减。以上情况使得单个位置的自由振动数据易出现病态方程,导致辨识精度不高。

在多个位置激励并采集自由振动数据进行辨识,可有效地克服以上问题,提高辨识精度和速度。

2 数值仿真

2.1 辨识精度验证

采用数值仿真验证算法的辨识精度,具体方法为:仿真谐振子自由振动,生成4个解调量采样数据,添加检测噪声,并用上述算法进行辨识。仿真使用的相关参数如表1所示。由于频差(0.628 mrad/s)在数值上小于阻尼差(0.838 mHz),阻尼差不能忽略,传统辨识方法失效,无法正确辨识频差和频率主轴。

表1 仿真参数

仿真中,分别在圆周角θ=0°和θ=22.5°位置进行激励,生成2组60 s自由振动数据用于辨识。统计100次仿真的辨识结果,如表2所示。辨识均值误差和均方差均很小,频差辨识均方差仅为0.73 μHz,频率主轴辨识均方差仅为0.12°,阻尼差辨识均方差仅为4.60 μHz,阻尼主轴辨识均方差仅为0.05°。

表2 辨识结果统计

由表1、2可看出,即使在频差小于阻尼差的条件下,本文提出的算法也能快速准确地辨识频差、频率主轴、阻尼差和阻尼主轴等参数。

2.2 测试时长的影响

仿真测试总时长对两位置法辨识精度的影响,结果如图1所示。频差和阻尼差的辨识均方差σ与测试时长T的关系为

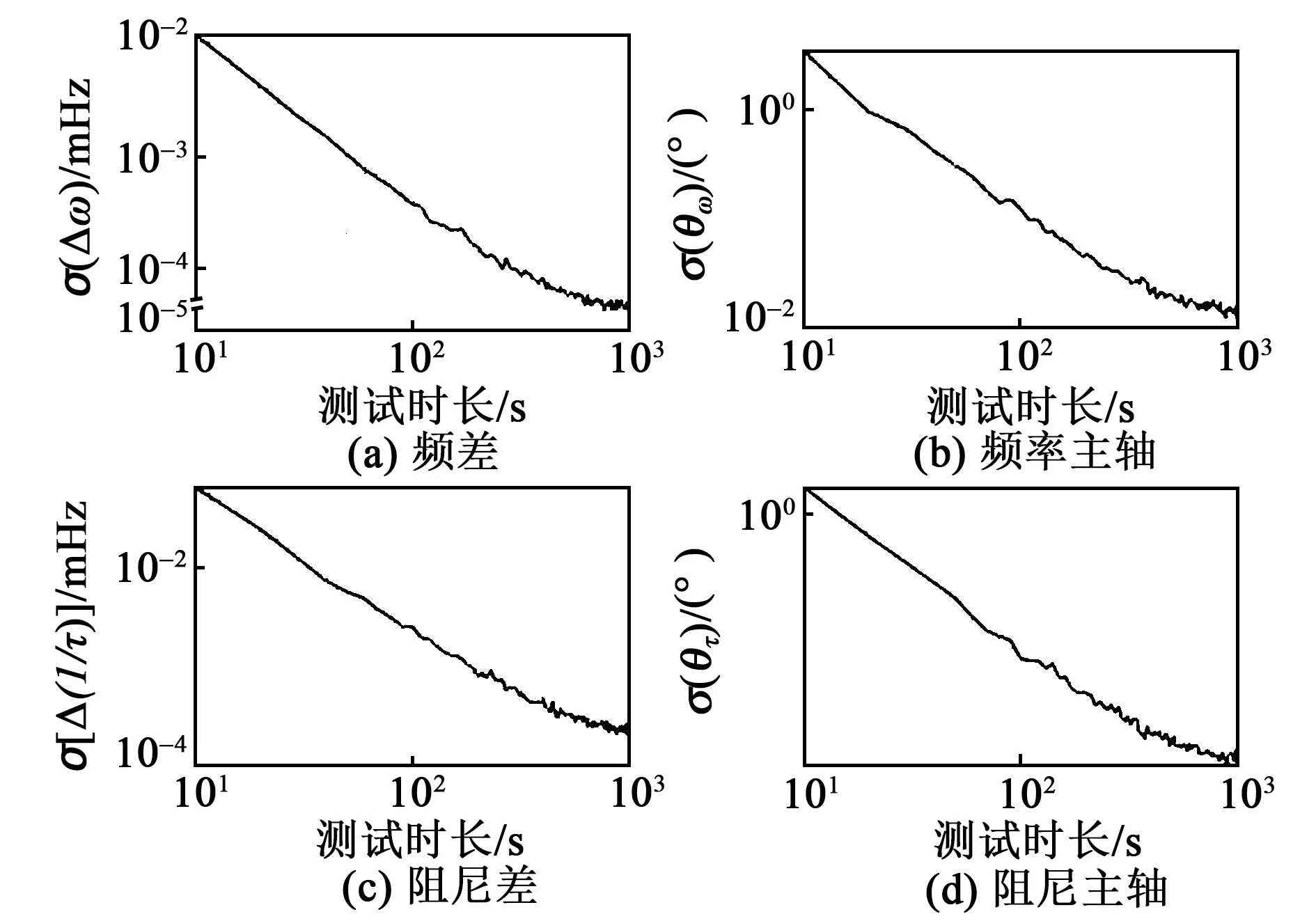
图1 测试时长对辨识均方差的影响

(23)

由图1可知,增加测试时长可有效地提高辨识精度。测试时长增加10倍,辨识精度提高约20倍。

2.3 激励位置数的影响

在总时长120 s不变的情况下,仿真研究激励位置数对辨识精度的影响。仿真中,激励位置在θ=0°～22.5°均匀分布。仿真得到的辨识误差均方差与位置数的关系如图 2所示。两位置法的频差辨识精度比单位置法提高了54倍,频率主轴辨识精度提升了41倍,阻尼差辨识精度提升了36倍,阻尼主轴辨识精度提升了45倍。随着位置数继续增加,辨识精度持续下降,原因是单次自由振动时长变短。

由图2可看出,在总时长不变的情况下,两位置法的辨识精度明显高于单位置法。

图2 激励位置数对辨识均方差的影响

3 实验验证

3.1 实验平台

基于清华大学自研的离子束修调系统(见图3(a))验证算法的辨识精度。修调系统内部采用平面叉指电极激励和光纤干涉仪检测方案,如图3(b)所示。

图3 离子束修调系统和激励、检测装置

3.2 实验结果

为了验证本文算法在频差小于阻尼差条件下的实际性能,选择一个阻尼差较大的谐振子,用本文的算法辨识频差和频率主轴,并用离子束将频差修调至最小,用两位置法批量进行参数辨识实验。

连续36组测试的结果如图4所示。统计结果如表3所示。谐振子的频差约0.100 mHz,阻尼差约8.154 mHz,频差在数值上远小于阻尼差。

表3 谐振子参数辨识结果统计表

图5为单次测试数据的拟合结果。由图可看出,变量E最大拟合误差约0.99%,变量H最大拟合误差约0.10%,变量R最大拟合误差约0.92%,变量S最大拟合误差约0.59%。参数辨识结果较好地拟合了实测数据。

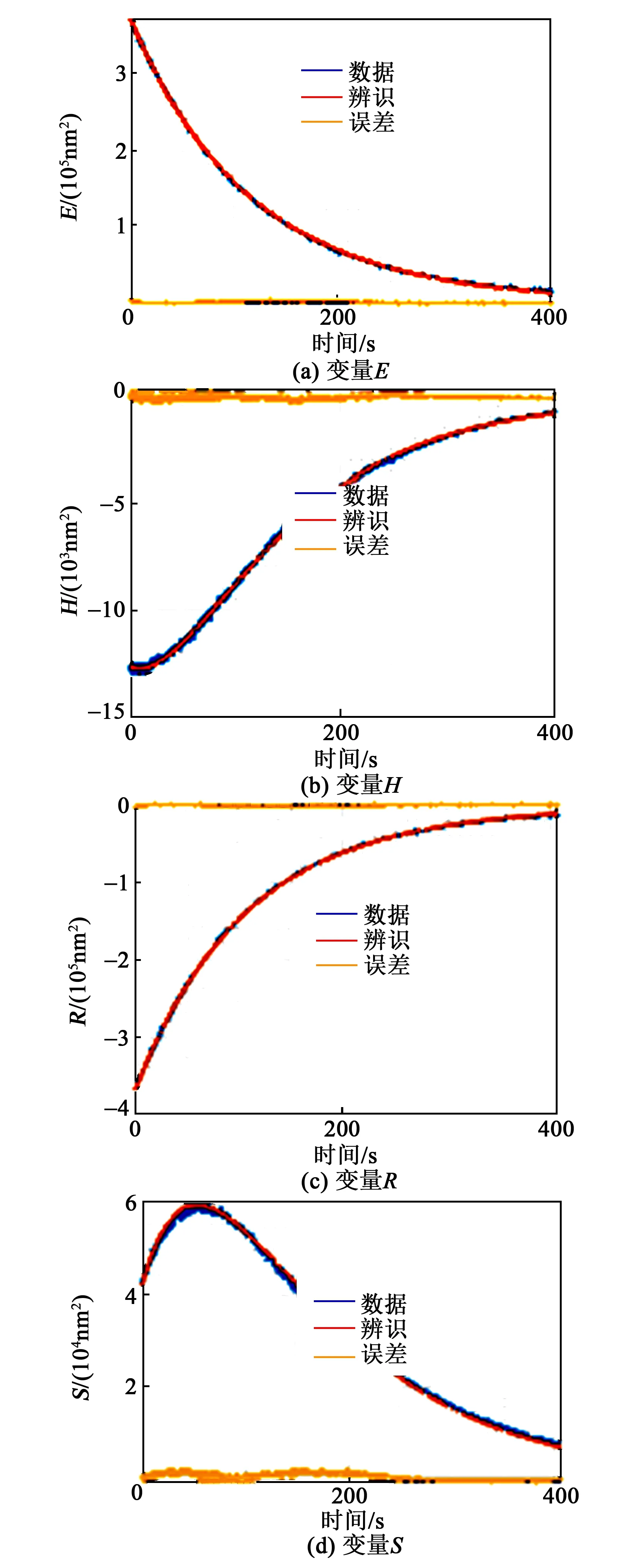
图5 实测数据与辨识结果对比

理论上,变量H是频率为Δω的衰减振荡曲线,但实测数据在400 s内没有表现出周期性,说明频差远小于2.5 mHz,进一步印证了参数辨识结果的正确性。

综上所述,即使在频差小于阻尼差的条件下,本文提出的辨识算法也能快速准确地辨识频差、频率主轴、阻尼差和阻尼主轴等参数。

4 结束语

针对传统算法不能辨识阻尼差和阻尼主轴,且频差和频率主轴辨识精度受阻尼差限制的问题,本文提出了一种基于变量E、H、R、S动力学方程的半球谐振子性能参数辨识算法。仿真和实验结果表明,在频差小于阻尼差的条件下,该算法能快速准确地辨识频差、频率主轴、阻尼差和阻尼主轴等参数。