细观结构特性对压电叠堆内部应力场的影响分析

姚佐聪,胡和平,高 乐,张仕明

(中国直升机设计研究所,江西 景德镇 333001)

0 引言

压电叠堆充分利用压电陶瓷的功率密度高,体积小,频响高及输出力大等特点,广泛应用于能源、电子、光学、生物医学及航空航天等领域[1-2]。

目前国内外针对压电叠堆的研究主要集中在其迟滞特性、精密控制及力学输出特性测试等方面[3-5],对压电叠堆自身细观结构相关的原理性分析较少,而涉及压电叠堆内部应力场环境探析的报道更少。主要原因是压电叠堆属于多层微结构,其三维细观建模涉及上百层微米级压电陶瓷片和附属电极,采用常规的CAE建模手段工作量大,耗时长,因此,对压电叠堆进行多层结构建模分析的文章都对模型进行了简化。如梁磊等[6]基于ANSYS分析了压电叠堆的位移特性,最多仅建立了10层压电陶瓷层。郝刚等[7]利用ABAQUS软件的二次开发功能对400层的压电叠堆进行了参数化建模,并分析了不同预应力对叠堆输出位移的影响,但所建立的模型未考虑电极和惰性陶瓷层的影响。以上模型对分析压电叠堆宏观力学输出特性有较好的准确性,但都无法对压电叠堆内部的应力场环境进行准确分析。

本文基于COMSOL Multiphysics有限元软件,结合平台提供的 M 语言,对成熟构型压电叠堆进行了参数化建模,通过理论分析对模型进行校验,并分析了几种细观结构特性对压电叠堆内部应力分布状态的影响规律,为压电叠堆型执行器的选型、可靠性设计和性能优化等提供依据[8]。

1 压电叠堆理论分析

在不考虑压电材料的迟滞、蠕变等非线性特性时,压电方程是描述压电材料应力-应变和电场-电位移间相互耦合的关系式:

(1)

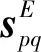
当忽略泊松效应的影响,只考虑压电陶瓷片第3方向(厚度方向)的极化效应时,式(1)可简化为

(2)

(3)

式中:δ为压电叠堆的总输出位移;t为单层压电陶瓷片的厚度;-T为对压电叠堆厚度方向施加的压力;A为叠堆的横截面积;U是施加的电压。

将式(3)整理为变形量表达式:

(4)

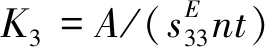
2 压电叠堆的有限元模型

COMSOL Multiphysics是一款模块化的多物理场有限元仿真建模与分析工具,广泛应用于各大研究领域[9-10]。

2.1 压电叠堆的参数化建模

利用COMSOL的模型开发器与APP开发器结合的方法,对含有活性段、过渡段及非活性段陶瓷层的压电叠堆进行了参数化建模。其中活性段含有PZT-5H压电陶瓷片和 AgPd电极各149层,该部分建模是在APP开发器中通过程序编译实现,从而避免了大量重复性工作。在活性段与两端非活性段之间各设置了两层0.25 mm的过渡陶瓷层,过渡段及两端非活性段同样采用PTZ-5H压电陶瓷,两层过渡段间及过渡段与非活性区间皆由1层电极隔开,故总电极层数为153层,该部分建模工作是在模型开发器中通过CAE操作完成。图1为压电叠堆的几何模型图,其总高度为20 mm。结构参数如表1所示。

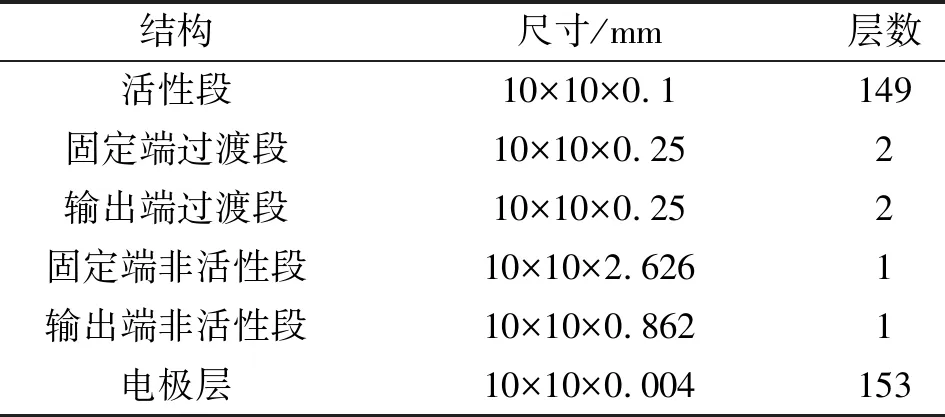
表1 压电叠堆的结构参数

图1 压电叠堆几何模型

本文采用的PZT-5H压电陶瓷来自COMSOl内置材料库,电极采用目前较先进的电极材料AgPd,其参数如表2所示。对于边界条件设置,通过APP程序编译实现“静电”接口中每相邻两层电极的正负交替电场施加,再根据不同的求解需求在“固体力学”接口中进行约束条件设置。由于叠堆几何体形状较规则,在进行网格划分时采用物理场控制的结构化六面体网格,该模型的参数化建模流程如图2所示。

表2 AgPd电极材料参数

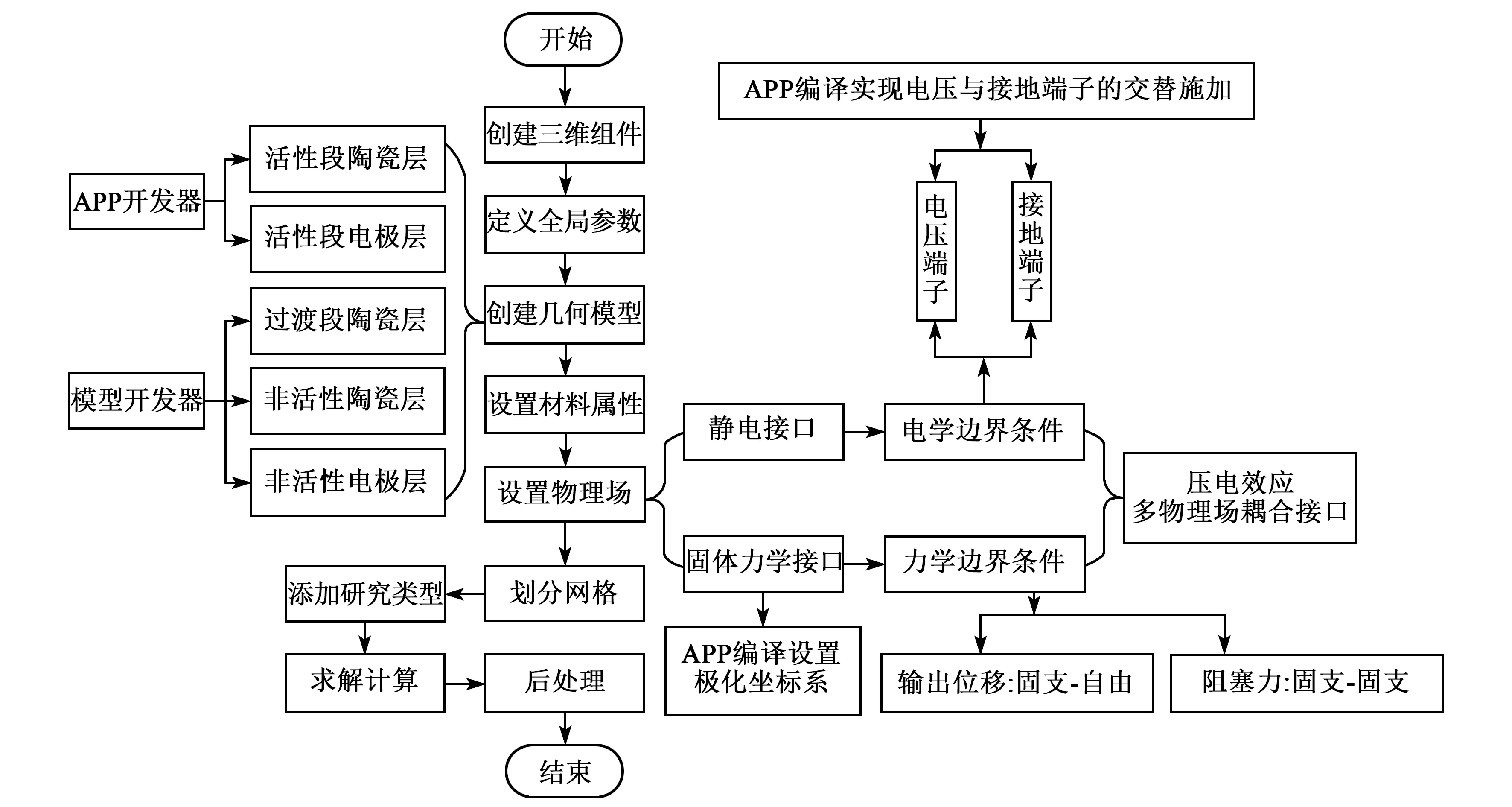
图2 压电叠堆的参数化建模流程

2.2 模型可靠性校验

由于压电叠堆的内部力场属于微观层面,通过理论或试验进行分析较难,故本研究采取对比宏观力学输出特性的方式,即通过仿真分析获得静态电压激励下的叠堆自由位移和阻塞力,并将仿真数据与式(4)计算的理论值进行对比,以验证模型的可靠性。

在COMSOL的模型开发器中设置电压变量及接地端子,再将该变量和接地端子通过程序编译赋予到每层压电陶瓷片的上下表面,最后在求解器中设置电压变量的初始值为0,步长为10 V,终止值为150 V,进行参数化扫描计算,其对应电场强度步长为0.1 V/μm,最大场强为1.5 V/μm。当力学边界条件为固支-自由时可得到1组叠堆自由位移仿真值,边界条件为固支-固支时可得到1组阻塞力仿真值。图3、4为仿真计算和理论计算的对比结果。由图可看出,仿真得到的自由位移和阻塞力与理论结果一致性良好,其微小误差可能来自理论解析式忽略了泊松效应的影响,有限元模型具有较好的准确性。

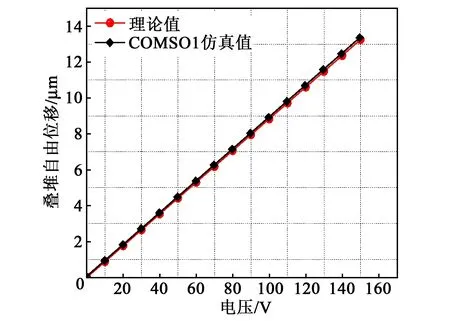
图3 压电叠堆自由位移计算对比

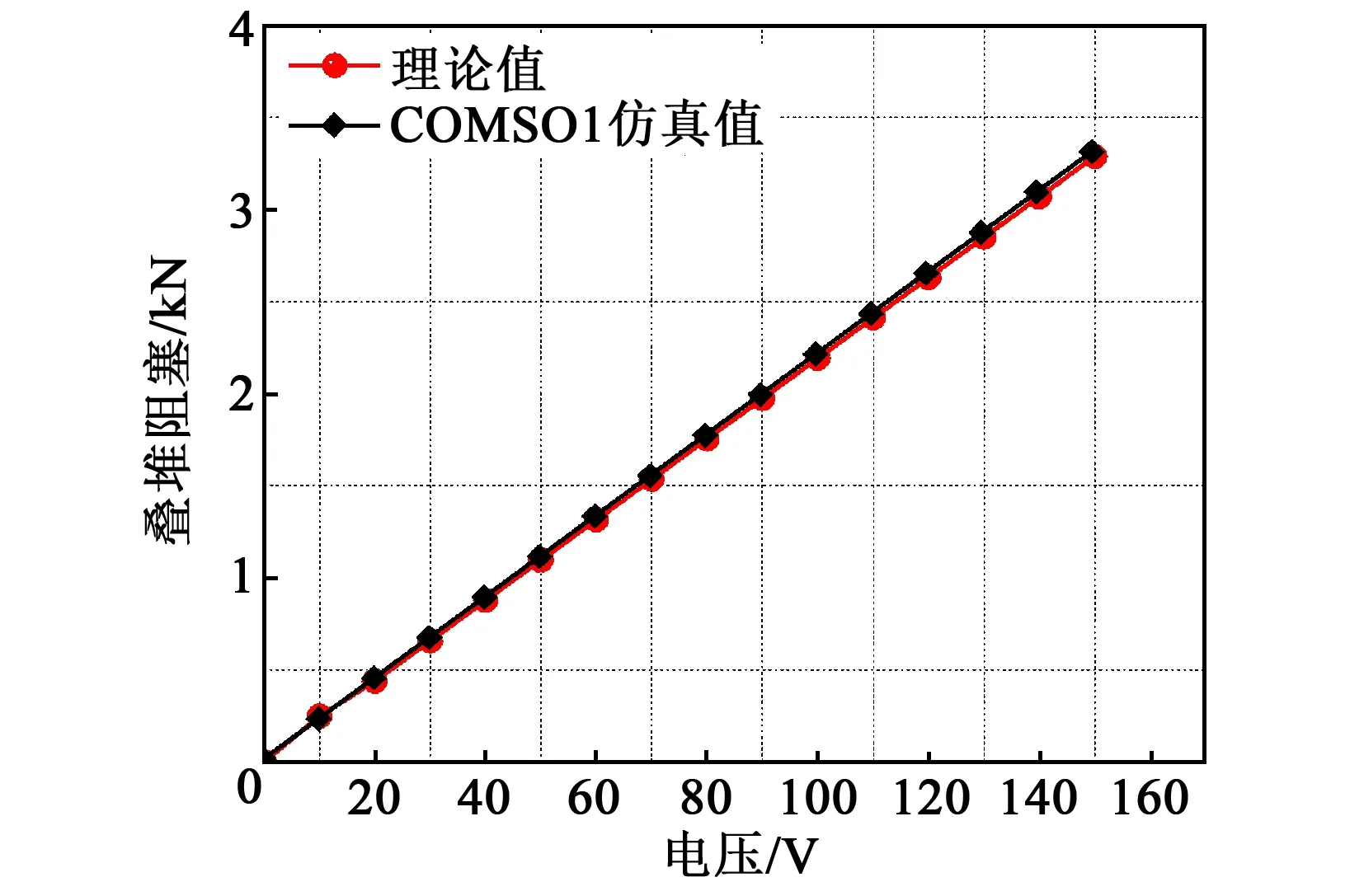
图4 压电叠堆阻塞力计算对比

3 仿真分析

压电叠堆内部的应力集中现象是影响其可靠性的主要因素之一,尤其是受到较大拉应力时容易发生损坏。因此,有必要对叠堆内部的应力分布情况进行分析,找出最大应力出现的部位,为压电叠堆的可靠性设计等提供支撑。

3.1 电极构型对压电叠堆内部应力的影响

压电叠堆的电极构型主要有全电极和叉指电极两种,第2节建立的压电叠堆模有限元模型采用全电极,与叉指电极相比,其在陶瓷片上下表面为交叉排列的正负分支电极,电极的非引出端有少量的尺寸缩进,犹如手指交叉形状。为避免因材料不同引起的叠堆内部性能差异,缩进部分由相同的PZT-5H惰性压电陶瓷进行填充,本研究取缩进尺寸为0.5 mm,如图5所示。此外,叉指电极叠堆在设置电学边界条件时较复杂,由于惰性陶瓷不导电,需要在电极与惰性陶瓷交界处设置介电屏蔽边界,本研究采用屏蔽材料为理想气体,其参数如表3所示。

表3 介电屏蔽材料参数

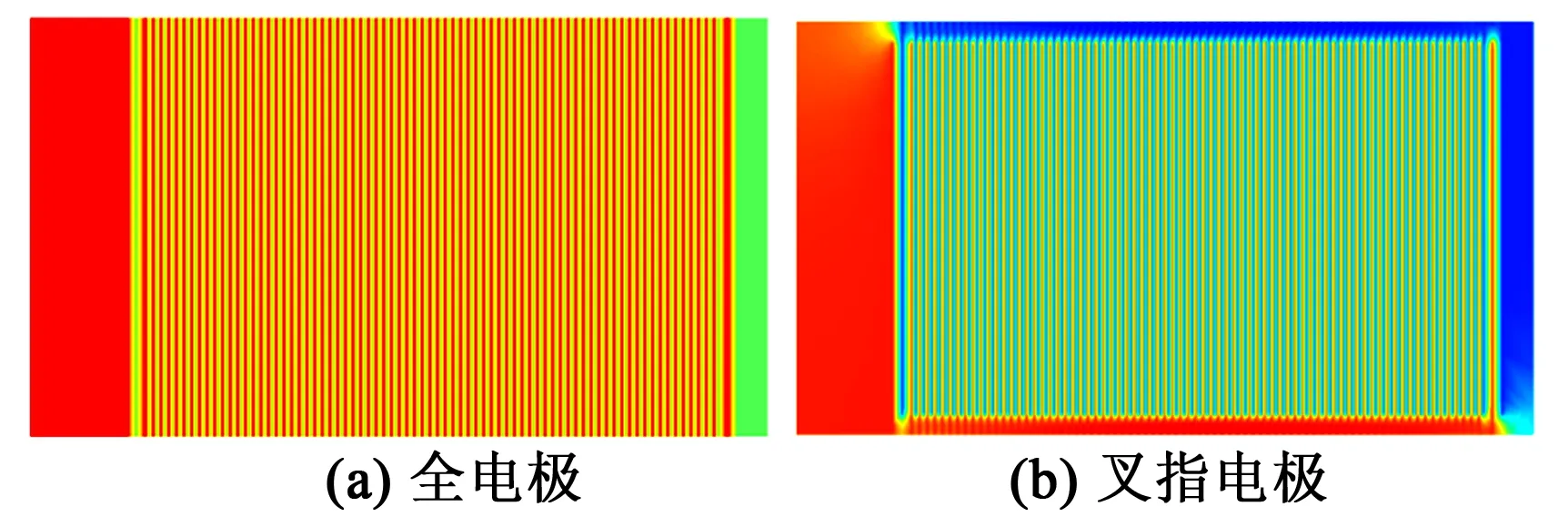
图5 电极构型图

对激励电压150 V、固支-固支边界条件下的两种构型压电叠堆进行应力分析,图6为二者的外部Mises应力分布云图。由图可看出,全电极叠堆的活性段陶瓷靠近中间部分的应力分布无明显的梯度变化,而两端越靠近过渡段陶瓷层的应力水平逐步增高,非活性段的边缘位置的应力较大;叉指电极型叠堆的应力主要分布在活性段的有效通电部分,惰性陶瓷和非活性段的应力水平较低。

为进一步量化分析各部位陶瓷层应力分布状态,将模型沿平行于陶瓷层平面进行剖切,并计算出x、y、z3个主方向上的应力值,剖切位置为活性段的两端面层(与过渡段交界层)和中部层这3个典型部位,结果如图7所示。

对压电叠堆的各剖切面进行定性和定量分析可以看出,对于全电极型压电叠堆, 活性段两端面陶瓷层的应力分布较均匀,输出端陶瓷层在x、y方向上的大应力值主要分布在靠近陶瓷层的4条边处,应力最大值分别为26.9 MPa、24.7 MPa,z方向的大应力值分布在陶瓷层中部区域,最大值在中心位置,为-37.1 MPa(负号表示压应力);固定端陶瓷层的应力分布和输出端类似,在x、y、z方向上的最大应力分别为27.4 MPa、25.6 MPa、-38.7 MPa;对于中部陶瓷层,x方向最大应力分布在陶瓷层的四条边缘处,为1.02 MPa,而中间区域应力水平较低;y和z方向最大应力集中在陶瓷层的4个角上,分别为0.98 MPa、-34.8 MPa,而中部区域应力水平相对较低,呈圆环状分布。

对于叉指电极型压电叠堆,各部位在x、y方向上的应力分布都较均匀,无明显的应力集中现象。而在z方向上,电极与惰性陶瓷的交界位置有明显的应力突变现象,为进一步观察该位置的应力分布情况,将压电叠堆沿陶瓷厚度方向再次进行剖切,结果如图8所示。由图可看出,在应力突变的位置,即电极与惰性陶瓷的交界处可以观察到明显的应力集中现象,且电势端的最大应力值高于零电势端,在x、y、z方向上应力分别为-159 MPa、-161 MPa和-217 MPa,其数值均远大于全电极型叠堆的最大应力值。

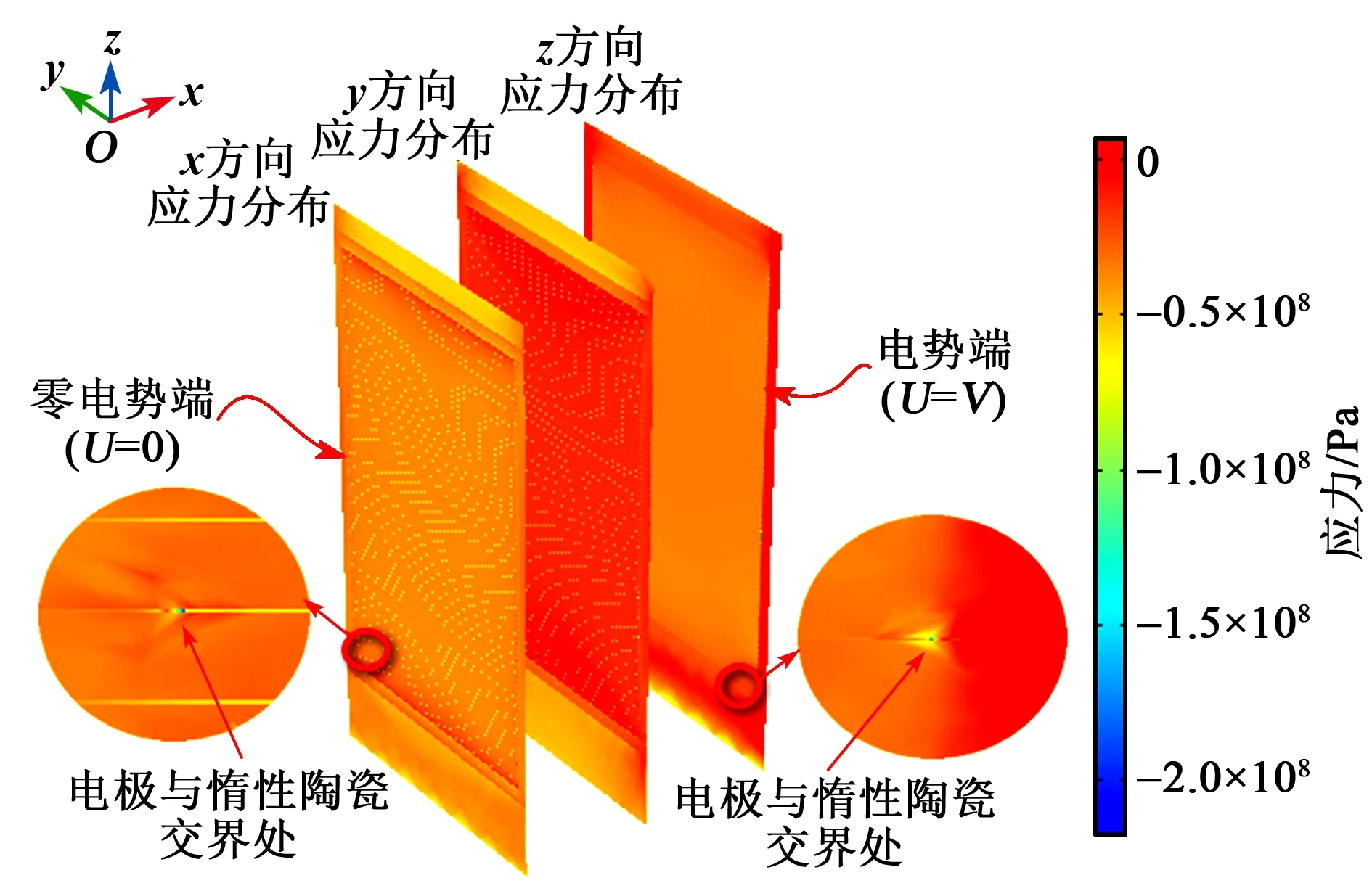
图8 叉指电极法向切面应力分布云图

3.2 陶瓷层厚度对压电叠堆内部应力的影响

针对全电极型压电叠堆,在控制压电叠堆总高度为20 mm,过渡段陶瓷厚度为0.25 mm不变,通过改变活段每层陶瓷的厚度,并调整活性段陶瓷的层数以及非活段区陶瓷的厚度,分别建立了不同厚度的压电叠堆仿真模型。 根据工程应用中常见的压电陶瓷尺寸,对厚度分别为60 μm、80 μm、90 μm、100 μm、105 μm、110 μm进行分析,表4为6种构型叠堆的结构参数。

表4 不同厚度叠堆的结构参数

由于压电陶瓷层厚度对叠堆许用电压的影响较大,在相同电场强度下,陶瓷层越厚,则需施加的等效电压越大。本文采取控制等效电场强度不变的方法,对等效电场强度为1.5V/μm时进行分析,其对应的等效电压与陶瓷厚度的关系如表5所示。

表5 等场强(1.5 V/μm)下电压与陶瓷厚度的关系

对活性段的典型部位陶瓷层进行应力分析,x、y、z方向最大应力随陶瓷厚度变化规律如图9～11所示。由图可看出,改变陶瓷层的厚度不影响应力集中的分布位置,只影响应力值的大小。其中x、y方向上的最大应力值随陶瓷厚度的增大而减小,z方向最大应力随陶瓷厚度增大而增大,且z方向的应力值明显高于x、y方向,这是由于z方向为极化方向,同时也是施加电场的方向;而对于同一应力方向的不同部位,固定端陶瓷层的应力水平最高,输出端次之,中部段最小。

图9 x方向最大应力随陶瓷厚度变化规律

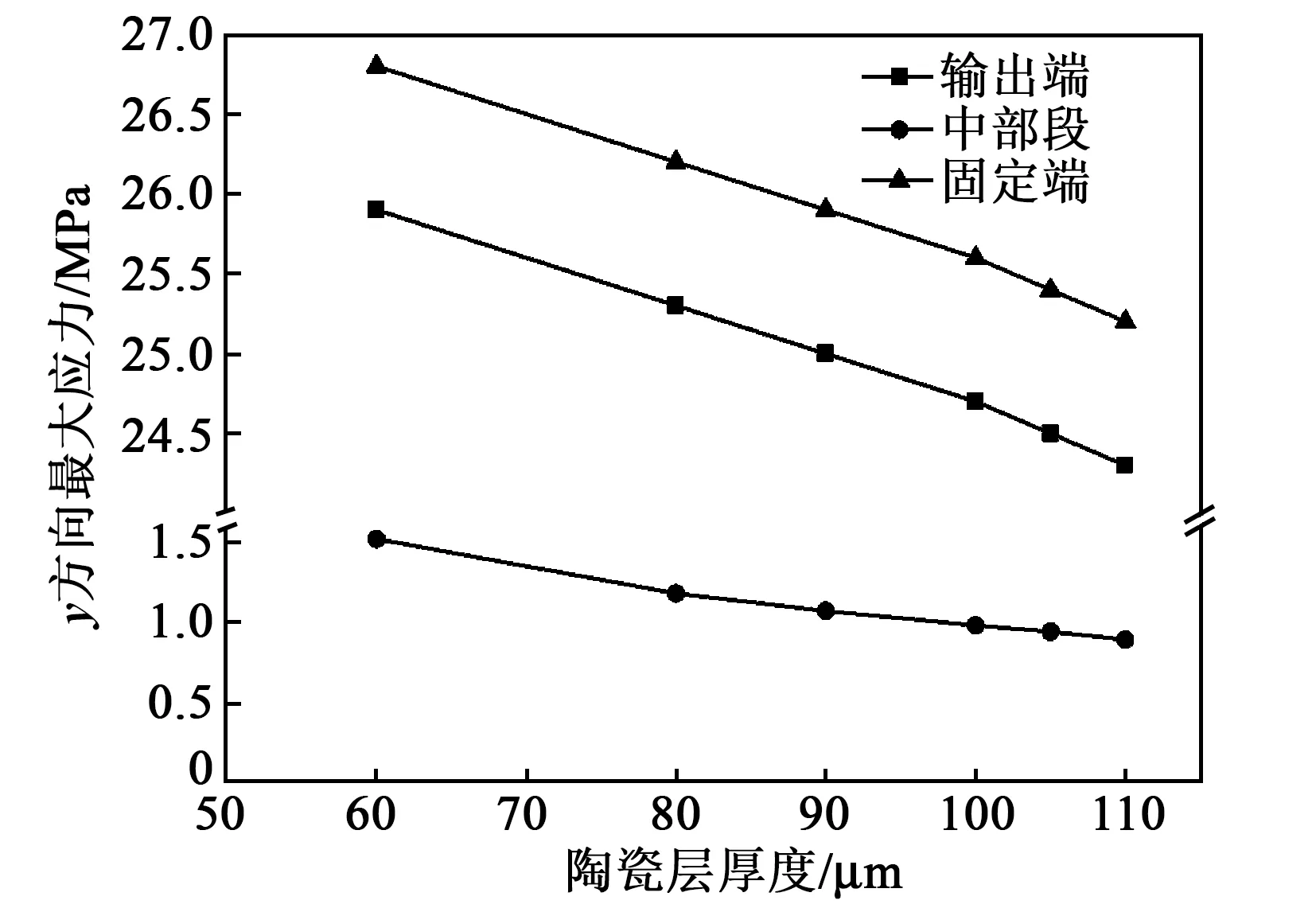
图10 y方向最大应力随陶瓷厚度变化规律

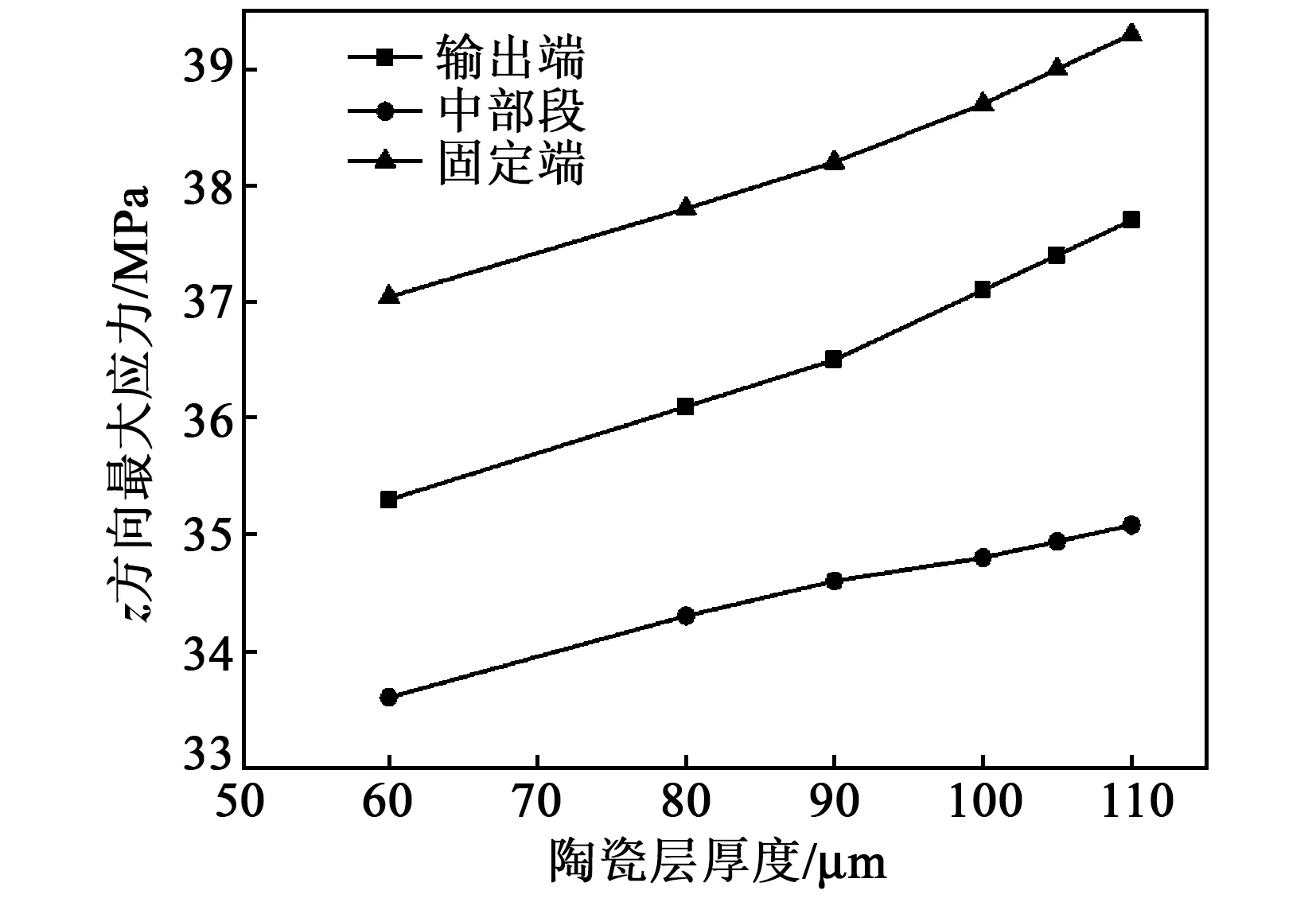
图11 z方向最大应力随陶瓷厚度变化规律

3.3 有无过渡段对压电叠堆内部应力的影响

为探究过渡段陶瓷对压电叠堆内部应力场的影响,建立了不含过渡段的全电极型压电叠堆有限元模型,与含过渡段模型3个典型部位主应力最大值进行了对比分析,结果如图12所示。

图12 有无过渡段对叠堆最大应力值的影响

由图12可看出,不含过渡段的压电叠堆在活性区两端处的最大应力高于含过渡段叠堆,而是否含过渡段对中部段陶瓷的最大应力无影响,且中间段陶瓷层x、y方向最大应力与两端陶瓷层的x、y方向相比有显著降低,这说明越靠近压电叠堆中部,陶瓷层受到泊松效应的影响越小,而产生作用的主要是压电效应,这也使得该部位陶瓷层的应力分布相对均匀,可靠性更好。

4 结论

本文对压电叠堆进行了参数化建模,并针对细观结构特性对应力场的影响做了分析,得出以下结论:

1) 发展了一种基于COMSOL平台和M 语言的参数化建模方法,可降低多层微结构压电叠堆的建模强度,并可实现各类结构参数的快速集中修改。

2) 通过对比有限元仿真和理论计算得到力学输出数据,验证了有限元模型具有较好的可靠性。

3) 通过分析,观察到全电极和叉指电极型叠堆的内部都存在应力集中现象,且叉指电极的最大应力值远大于全电极,分布位置在电极与惰性陶瓷的交界面。

4) 改变陶瓷层的厚度不影响叠堆内部应力集中的分布位置,切向(x、y方向)最大应力值随陶瓷厚度的增大而减小,法向(z方向)最大应力随陶瓷厚度增大而增大。

5) 在压电叠堆活性段与非活性段之间设置过渡段陶瓷,可有效地减少过渡部位活性陶瓷的最大应力集中值,增加压电叠堆的可靠性。

本研究发展了一种针对压电叠堆的建模和分析方法,能够对叠堆内部任意位置应力/应变状态进行剖析,为压电叠堆的构型优化设计、可靠性验证以及性能预测等提供了一种新的分析手段。