半球谐振子不平衡力的推导及与驻波关系研究

刘 奎,于鑫海,段 杰,苏定宁,赵思晗,李绍良,赵万良

(1. 上海航天控制技术研究所,上海 201109;2. 上海惯性工程技术研究中心,上海 201109)

0 引言

半球谐振陀螺是一种新型的高精度陀螺仪,具有长寿命、高稳定性、高可靠性及断电可长时间保持等优点,已成为国内外的研究热点[1-3]。半球谐振陀螺的理论基础最早可以追溯到1890年,英国科学家Bryan发现敲击并旋转酒杯会听到“差拍”,表明酒杯中的驻波相对空间旋转[4]。20世纪,美国科学家Lynch等[5]对半球谐振陀螺理论的进一步发展与性能提升做出了重要贡献。由于在实际加工过程中谐振子存在误差,因此,谐振子并非理想的轴对称结构。这会导致谐振子产生不平衡质量,当谐振子做四波腹振动时将对基座产生额外的作用力,这些不平衡力使谐振子偏离理想的四波腹振动,从而对陀螺精度产生影响[6-7]。

Shatalov等[8]建立了谐振子质量与阻尼非对称分布的动力学方程,同时采用平均法求解动力学方程。Shatalov等[9]通过引入新的变量研究振动壳体缓慢旋转时质量不平衡的影响。Zhbanov等[6]讨论了谐振子由不平衡力引起的支撑杆的线性振动,得到了半球谐振陀螺漂移与不平衡质量及偏心之间的关系式。同时,多种修调技术与方法也被提出来用于谐振子不平衡质量的去除[10-12]。

为了对谐振子不平衡质量的去除提供理论依据,并进一步提升半球谐振陀螺的精度,需要对谐振子不平衡力的计算与分析展开研究。本文首先总结了半球谐振子动力学计算时采用的基本假设,然后基于该假设计算谐振子的不平衡力,给出不平衡力的理论公式。最后通过数值计算研究不平衡力与驻波方位之间定量的关系,为分析不平衡质量对陀螺精度的影响提供参考。

1 半球谐振子动力学分析基本假设

采用球坐标系对半球谐振子的运动进行分析,谐振子上任意一点的坐标可用(r,θ,φ)描述,如图1所示。

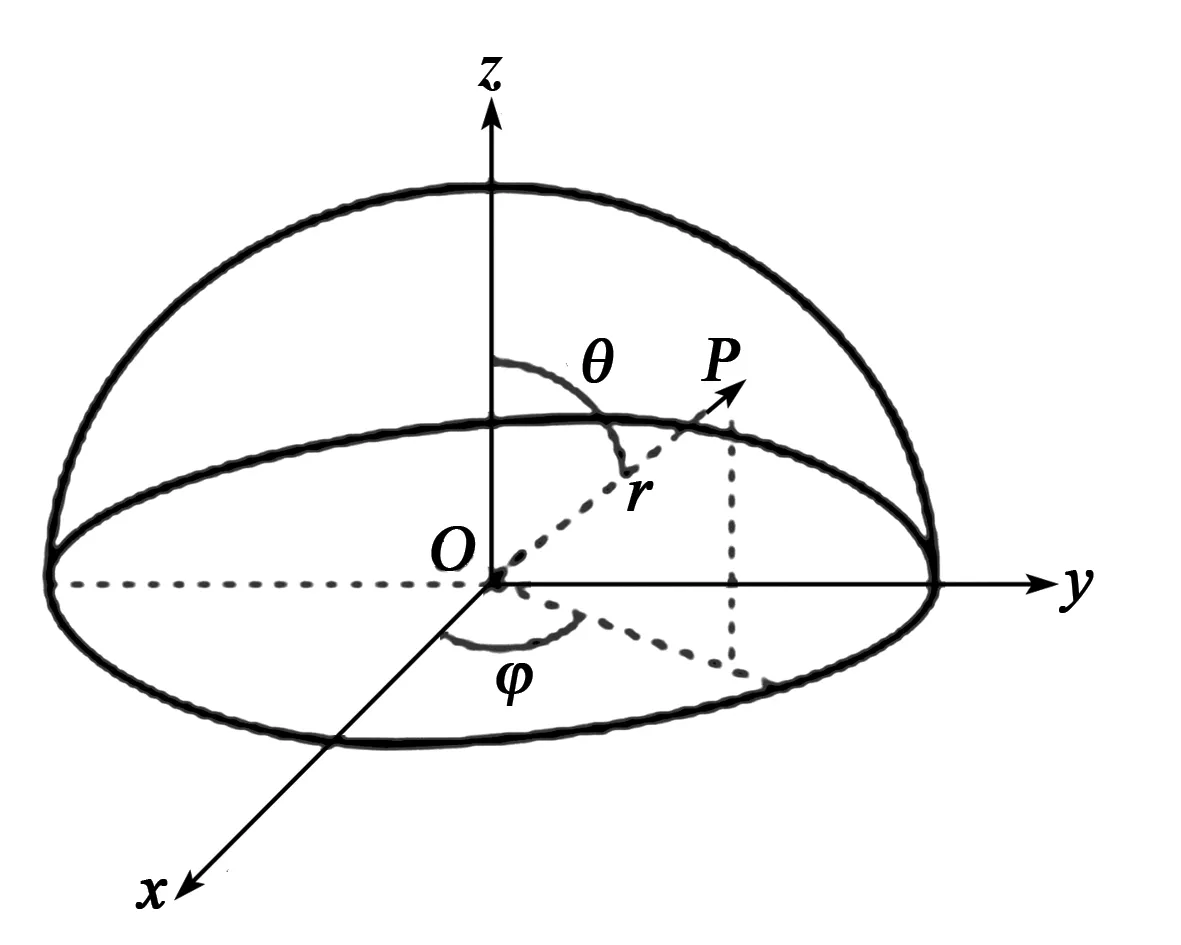
图1 半球谐振子的球坐标系定义

为了对半球谐振子做动力学分析与研究,需要基于半球谐振子的结构形式建立基本的假设。目前对半球谐振子的研究主要是基于薄壳理论,该理论的基本假设主要包括:

1) 忽略垂直于中面方向正应变。

2) 中面法线在变形前后仍与中面垂直。

3) 中面不可拉伸。

此外,为了方便对谐振子的不平衡质量进行分析,这里假设不平衡质量沿谐振子周向分布。将不平衡质量沿周向展开为傅里叶级数,有:

(1)

式中:r0为谐振子的平均密度;∈n为第n阶不平衡质量的相对值;φn为第n阶不平衡质量的方位角。

2 半球谐振子不平衡力的计算

设球面上各点的位移为

(2)

式中:x(t),y(t)为未知函数;U(θ),V(θ),W(θ)为球壳的瑞利函数。

根据薄壳理论的基本假设,可得半球壳上各点位移应满足方程:

(3)

式中u、v、w分别表示球壳上各点在x、y、z方向的振动位移。将坐标φ分离,并利用式(2)可得关于坐标θ的二阶微分方程:

V″sin2θ-V′sinθcosθ-3V=0

(4)

同时在半球顶部有ur=uθ=uφ=0,所以可解得:

(5)

将式(5)代入式(3)可得:

(6)

以及:

(7)

最终可得球壳的瑞利函数:

(8)

由于谐振子的不平衡力主要受周向不均匀质量的影响,因此,在研究谐振子的不平衡力时一般假设谐振子的质量沿周向不均匀分布,并将其沿周向展开为傅里叶级数,如式(1)所示。

设谐振子的振动位移为

(9)

式中:φ0为驻波方位角;A为谐振子的振幅;ω为谐振频率。

将式(9)代入式(2),并对式(2)求导可计算球坐标系下球面上各点的加速度:

(10)

为了方便计算直角坐标系下的不平衡力,将球坐标系下的加速度投影到直角坐标系。

(11)

由此可计算谐振子在做四波腹振动时的惯性力为

(12)

式中:R为谐振子半径;a=axe1+aye2+aze3为谐振子上各点的加速度,ei(i=1,2,3)为直角坐标系下的基矢量。

将式(1)、(11)代入式(12)并积分得到谐振子在做四波腹振动时的不平衡力为

(13)

由式(13)可看出,一、三阶不平衡质量会引起水平方向的不平衡力,二阶不平衡质量仅会引起竖直方向的不平衡力。

3 谐振子不平衡力的计算

表1为谐振子参数的典型值。将表1中参数代入式(13)可计算出各阶不平衡力的大小,如图2～4所示。

表1 谐振子参数的典型值

图2 一阶不平衡力的计算

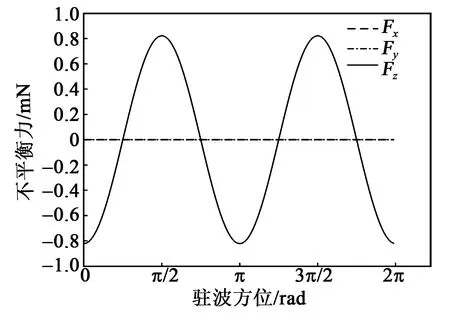
图3 二阶不平衡力的计算

4 谐振子不平衡力与驻波的关系

假设各阶不平衡质量的角度方位均为0,计算驻波在0～2π区间内旋转时,各阶不平衡力的大小与驻波方位间的关系,如图5～7所示。

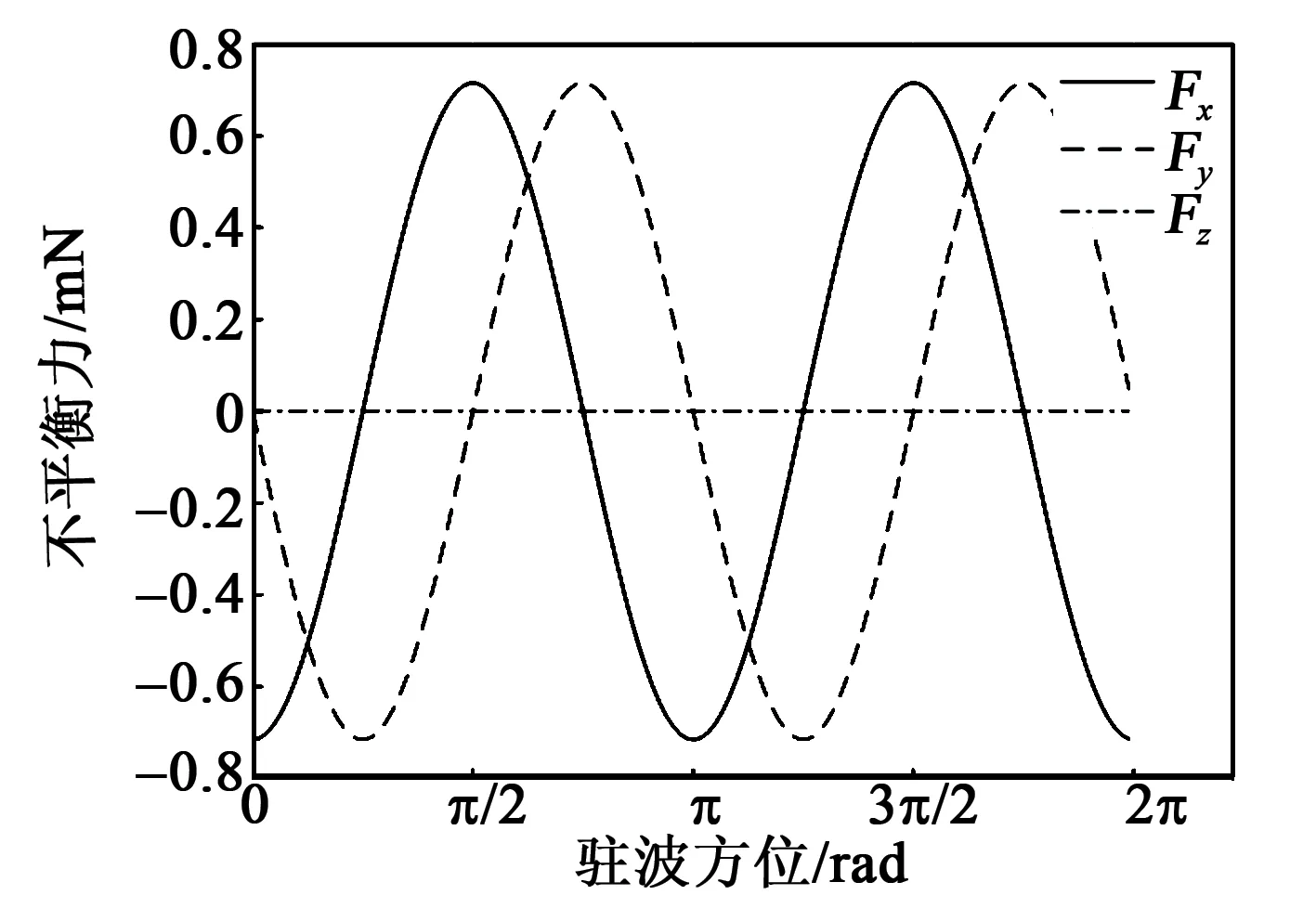
图5 一阶不平衡力与驻波方位之间的关系

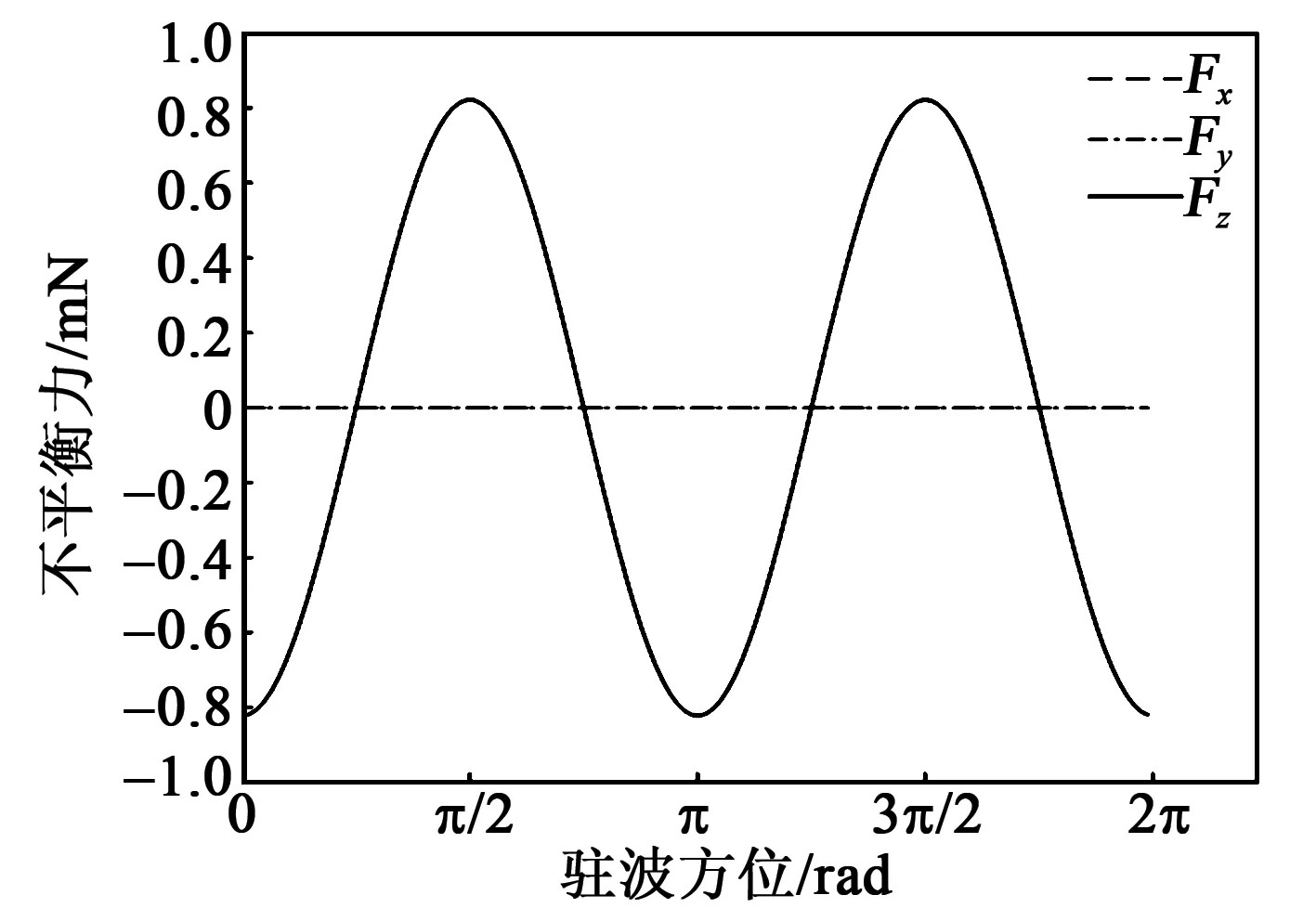
图6 二阶不平衡力与驻波方位之间的关系

5 结束语

本文研究了谐振子不平衡质量引起的不平衡力,给出了不平衡力计算的详细推导过程。在此基础上,通过数值仿真计算了谐振子典型值下各阶不平衡力的大小,并计算了各阶不平衡力与驻波方位之间的关系。研究表明,一、三阶不平衡质量仅引起水平方向的不平衡力,二阶不平衡质量仅引起竖直方向的不平衡力。同时,驻波方位在0～2π区间内各阶不平衡力均出现2个周期。