基于自校准技术的半球谐振陀螺正交误差的辨识补偿

苏鹤鸣, 陈朝春,文 路,肖 凯,王灵草,韩世川,王 涵,林翠平 刘东生,雷 霆

(1.中国电子科技集团 第二十六研究所,重庆 400060;2. 重庆市固态惯性技术企业工程技术研究中心, 重庆 401332;3. 重庆市固态惯性技术工程实验室, 重庆 401332)

0 引言

半球谐振陀螺(HRG)是一种新型全固态振动陀螺,近年来因其优良的C-SWaP特性而成为惯性导航领域的研究热点[1-4]。由频率裂解和阻尼不均匀引起的周向误差是产生陀螺驻波漂移误差的主要原因[5-9]。

由于外部环境等因素,正交误差具有时变性。本文在静电刚度校正技术的基础上,结合自校准算法,提出了一种实时校准正交误差的理论模型,并基于此对两件套平面电极的半球陀螺进行了理论仿真和实验验证。由于陀螺各个控制环路之间的耦合效应对正交误差的辨识影响较大,所以本文还对陀螺各个控制环路之间的耦合效应进行了建模分析和辨识补偿,并基于此对两件套平面电极陀螺进行了正交误差的实时辨识和补偿。

1 正交误差理论模型

图1为半球谐振子的等效振动模型。图中,坐标系xOy为理想状态下振子的振动主轴,坐标系τxOτy为周向阻尼不均匀时振子的最大和最小阻尼轴,坐标系ωxOωy为存在频率裂解时振子的最大和最小谐振频率轴,θω是振子最大谐振频率轴ωx与x轴的夹角,θτ是振子最大谐振频率轴τy与x轴的夹角。根据Lynch提出的广义的振动陀螺运动方程[10]:

图1 引入阻尼不均匀和频率裂解的非理想谐振子模型

[xcos(2θω)+ysin(2θω)]=Fx

(1)

[-xsin(2θω)+ycos(2θω)]=Fy

(2)

(3)

(4)

(5)

(6)

设矢量形式的方程通解为

(7)

其中:

(8)

(9)

式中:a,q分别为谐振子等效傅科摆的椭圆轨迹的长半轴和短半轴;θ为谐振子驻波角度,φ′为谐振子振动信号的初始相位。

设解调参考信号为

v=R[Ce-i(ωt+φ)]

(10)

其中φ为谐振子振动信号的初始相位。且:

C=e-iσ2θz0eiδφ

(11)

δφ=φ-φ′

(12)

联立式(1)、(2)、(7)、(10),得到当存在频率裂解和周向阻尼不均匀的情况下,正交控制环路的原理方程:

(13)

其中:

Q=2aq

(14)

E=a2+q2

(15)

(16)

(17)

2 相位误差辨识和补偿

由于陀螺振荡信号与参考信号之间存在相位差δφ,陀螺幅度控制环路的fas和驻波角控制环路fqc与fqc存在耦合现象。为了保证误差辨识的精度,必须先对各个环路之间的耦合进行解耦。根据谐振子运动轨迹方程(7)和参考信号方程(10)可得:

L=(a2-q2)e-2iδφ

(18)

通过对L计算量的实部、虚部比值即可得到相位差δφ,并根据这个值补偿修正各个环路之间的耦合量。

图2为正交误差实时辨识补偿环路的设计框图。将采集到的陀螺谐振子振动信号传输至自校准算法的误差辨识模块,得到陀螺正交误差后传输至陀螺控制程序中误差补偿模块,经过误差补偿后输出陀螺控制力,最后通过D/A等模块施加至陀螺谐振子电极,实现控制闭环。

图2 正交误差的实时辨识补偿的设计框图

图3(a)、(c)分别为驻波进动状态下有、无相位误差时正交误差的辨识与补偿结果。图中,蓝色曲线为信号解调端采集到的实时信号,红色曲线为误差辨识模块实时推算出的信号,绿色曲线为经过误差补偿模块后输出的正交控制信号。

图3 驻波角进动状态下相位误差有无时正交误差的辨识与补偿结果

由图3(a)可看出,当存在相位误差δφ时,红、蓝色曲线不重合,表明辨识信号与采集信号匹配度较差,补偿正交误差后,正交控制环路中还存在直流偏置量,这与理论式(13)相吻合。由图3(b)可看出,当补偿相位误差δφ后,红、蓝色曲线重合,表明辨识信号与采集信号匹配度良好,补偿正交误差后,正交控制环路的控制量无直流偏置量。

图3(b)、(d)分别为图3(a)、(c)的细节放大图,绿色与蓝色曲线的噪声水平相同,这说明本文采用的误差补偿方式在降低正交误差影响的同时,对正交控制环路的控制精度影响很小。

除相位误差δφ外,陀螺电路的检测和驱动增益矩阵的存在也会造成各个控制环路的耦合现象。为了确定检测和驱动增益矩阵对正交误差辨识和补偿的影响,去除增益矩阵并采集数据,图4(a)、(b)分别为有、无相位误差对正交误差辨识和补偿结果的影响。图中,蓝色曲线为信号解调端采集到的实时信号,红色曲线为误差辨识模块实时推算出的信号,绿色曲线为经过误差补偿模块后输出的信号。比较图3、4可以看出,增益校正矩阵的有无对于正交误差辨识和补偿结果的影响很小。产生这种现象的原因是:增益校正矩阵引入的控制环路耦合项是sin(2θ)和cos(2θ)的函数,在正交误差辨识过程中,会将这个误差直接归类于正交误差中,其影响在误差补偿模块中被补偿项抵消。这也侧面说明本文所提出正交误差辨识补偿方案的适用性较强,对陀螺检测和驱动电路中增益和相位误差不敏感。

图4 驻波角进动状态下无增益校正矩阵时,相位误差对正交误差的辨识与补偿结果的影响

3 不同工作模式下正交误差的实时辨识补偿

半球谐振陀螺具有多种工作模式,每种工作模式下,正交控制环路控制量的表现形式不同。下面对不同的工作模式下正交误差的辨识补偿结果进行分析。

图5是力平衡模式下驻波角为0°时,正交误差的辨识和补偿结果。图中,蓝色曲线为信号解调端采集到的实时信号,红色曲线为误差辨识模块实时推算出的信号,绿色曲线为经过误差补偿模块后输出的信号。正交误差的存在使得正交环路控制量存在一个偏置,误差补偿后正交环路控制量的均值被拉回0值,并且补偿后的控制精度与补偿前一致。

图5 力平衡模式下正交误差的辨识补偿结果

图6是全角模式下驻波位置为3.8°时正交误差的辨识和补偿结果。图中,蓝色曲线为信号解调端采集到的实时信号,红色曲线为误差辨识模块实时推算出的信号,绿色曲线为经过误差补偿模块后输出的信号。由于此时陀螺驻波角进动速度较小,正交误差的影响与力平衡模式下类似。对比图5、6可看出,不同驻波角位置的正交误差不同。

图6 全角模式下正交误差的辨识补偿结果

图7为全角模式虚拟进动情况下正交误差的辨识补偿结果。图中,蓝色曲线为信号解调端采集到的实时信号,红色曲线为误差辨识模块实时推算出的信号,绿色曲线为经过误差补偿模块后输出的信号。由于驻波进动,补偿前的正交误差随角度变化呈正弦变化,正交误差的补偿效果更明显。

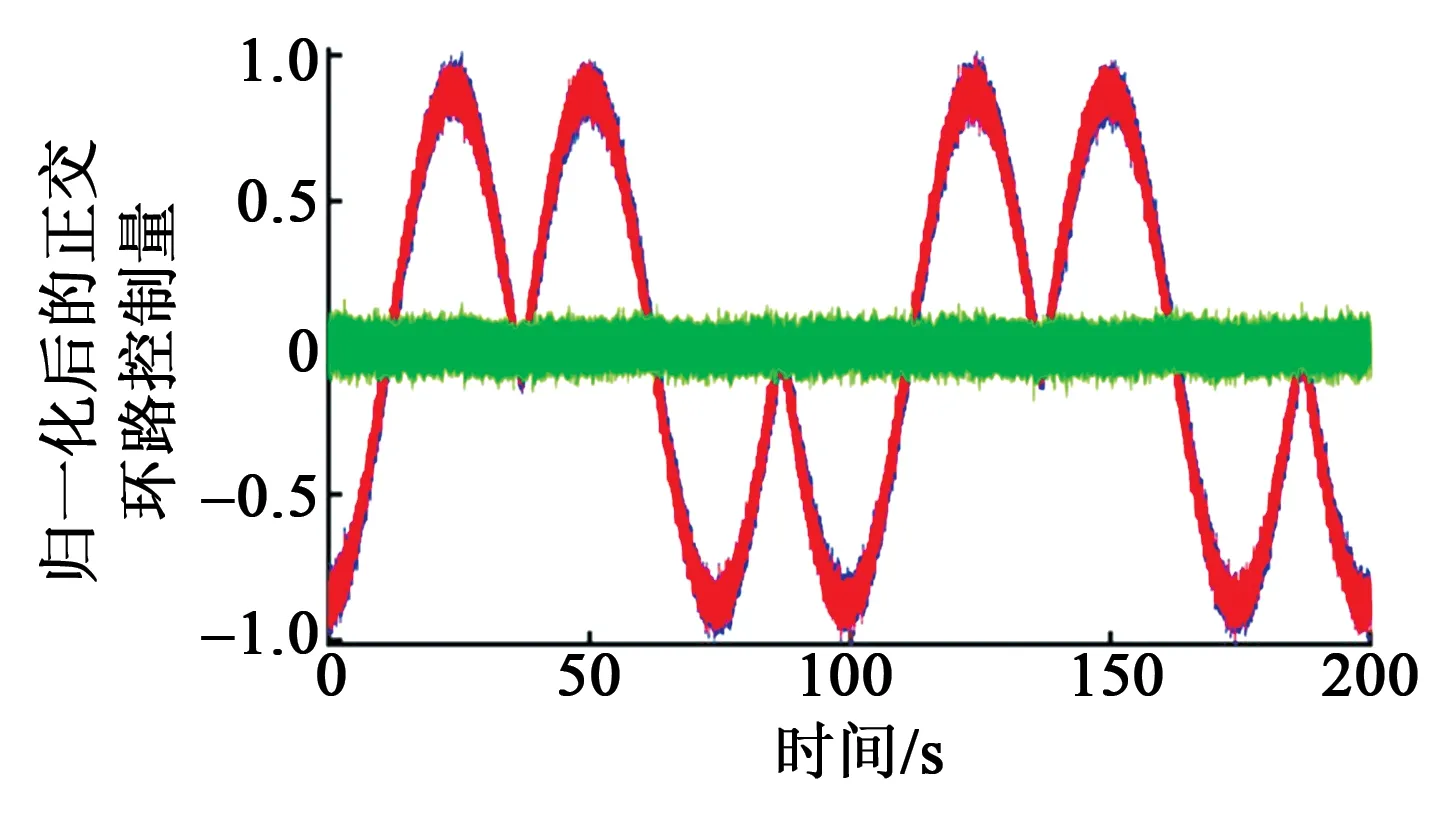
图7 全角模式虚拟进动情况下正交误差的辨识补偿结果

4 结束语

本文在静电刚度校正技术的基础上,结合自校准算法,提出了一种实时校准正交误差的理论模型,并对两件套平面电极的半球谐振陀螺进行了理论仿真和实验验证。结果表明,该方案适用于半球谐振陀螺的力平衡和全角两种工作模式,且适用于虚拟进动情况。此外,本文所提出的补偿方案不会影响正交环路的控制精度,对陀螺检测和驱动电路的增益和相位误差不敏感。