面向蜂巢式微机电陀螺模态交换工作模式的卡尔曼滤波

陈亮潜,苗桐侨,李青松,王 鹏,李军建,吴学忠,席 翔,肖定邦

(国防科技大学 智能科学学院, 湖南 长沙 410073)

0 引言

微机电系统(MEMS)陀螺仪作为一种用于测量角度、角速率的传感器,其针对不同应用场合的动态性能已受到人们关注[1-2]。目前由于谐振结构和测控电路的影响,微机电陀螺的输出噪声难以得到有效抑制[3-4]。实际应用中,常出现陀螺噪声性能与实际输出精度要求不匹配情况[5]。如静态的惯性寻北定向应用中,陀螺仪被用于敏感地球自转角速率,因此只需很小的动态性能,但对陀螺零偏稳定性要求极高。对于此类应用,陀螺仪较大的输出噪声使地球自转角速率信息被淹没在噪声中。

实际上,在惯性寻北中,较长的寻北时间是为了保证寻北仪中陀螺仪及其他传感器的采样精度,进而满足寻北解算精度而采用的一种对采样数据的时间序列处理方法[6-7]。对于寻北应用,人们通过一定的寻北时间得到的传感器采样数据通常经过平滑滤去噪声,以得到更准确的寻北结果,此时寻北精度取决于平滑后采样数据的噪声水平。同样,小波分解也是用于提取时间序列主趋势的有效手段,其与平滑均是离线方法[8],需要一定的采样数据量才能保证其精度。而卡尔曼滤波作为一种在线的时间序列处理方法,被广泛用于导航制导、航空航天及目标跟踪等各个领域[9-10]。

本文以蜂巢式微机电陀螺为研究对象,对其模态交换工作模式下最终用于寻北中北向解算的陀螺输出进行分析建模,建立可用于缩短寻北时间的卡尔曼滤波模型,并进行测试验证。为缩短寻北仪的寻北时间提供了新思路和新方法。

1 基于模态交换工作模式的蜂巢式微机电陀螺

1.1 蜂巢式微机电陀螺

本文研究的蜂巢式微机电陀螺,其主要由谐振结构和电极组成,结构如图1(a)所示。谐振结构包括锚点和框架结构两部分。锚点与底座固定连接,并起支撑作用。框架结构悬浮在空中并起敏感角速度作用。框架结构包括内部蜂巢形的辐条和外围挂载的质量块。与衬底固定连接的电极包括谐振框外的电极(外部电极)和谐振框内的电极(内部电极)。在电极和相邻谐振结构间形成等效平行板电容。陀螺仪的振动可通过检测电容的变化来检测。陀螺工作在二阶简并模态下,其工作模态示意图如图1(b)所示。陀螺的加工工艺流程参考文献[11-12]。经过测试,陀螺两个工作模态的品质因数Q≈57×104,谐振结构的初始频差为0.183 Hz[13]。测试的陀螺样机如图2所示。

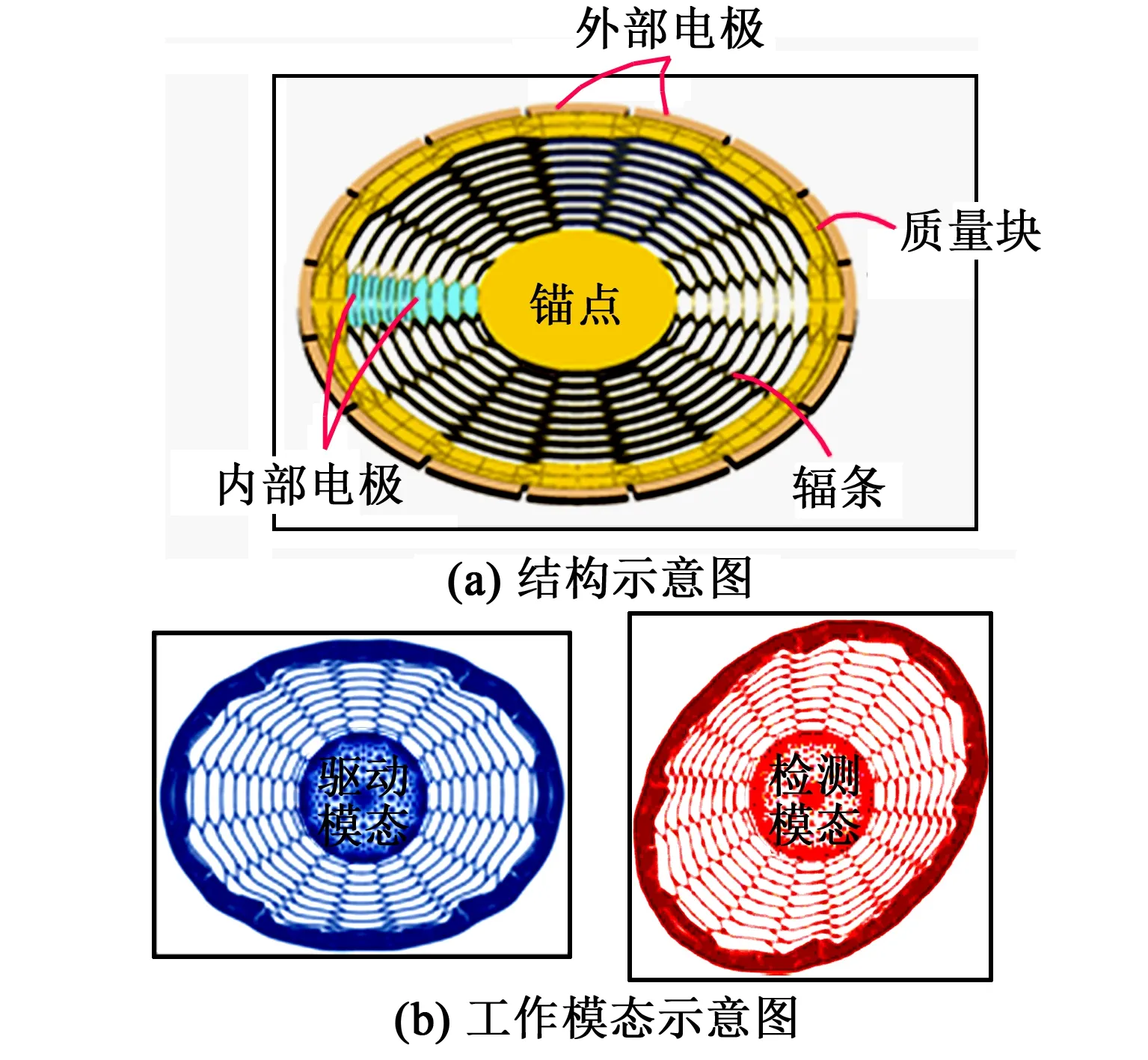
图1 蜂巢式微机电陀螺结构与工作模态示意图

图2 蜂巢式微机电陀螺样机

1.2 模态交换技术

图3为模态交换与二自由度动力学模型示意图。如图3(b)所示,根据文献[14]中报道的二自由度集中质量振动模型,蜂巢式陀螺工作在力平衡模式下的输出为

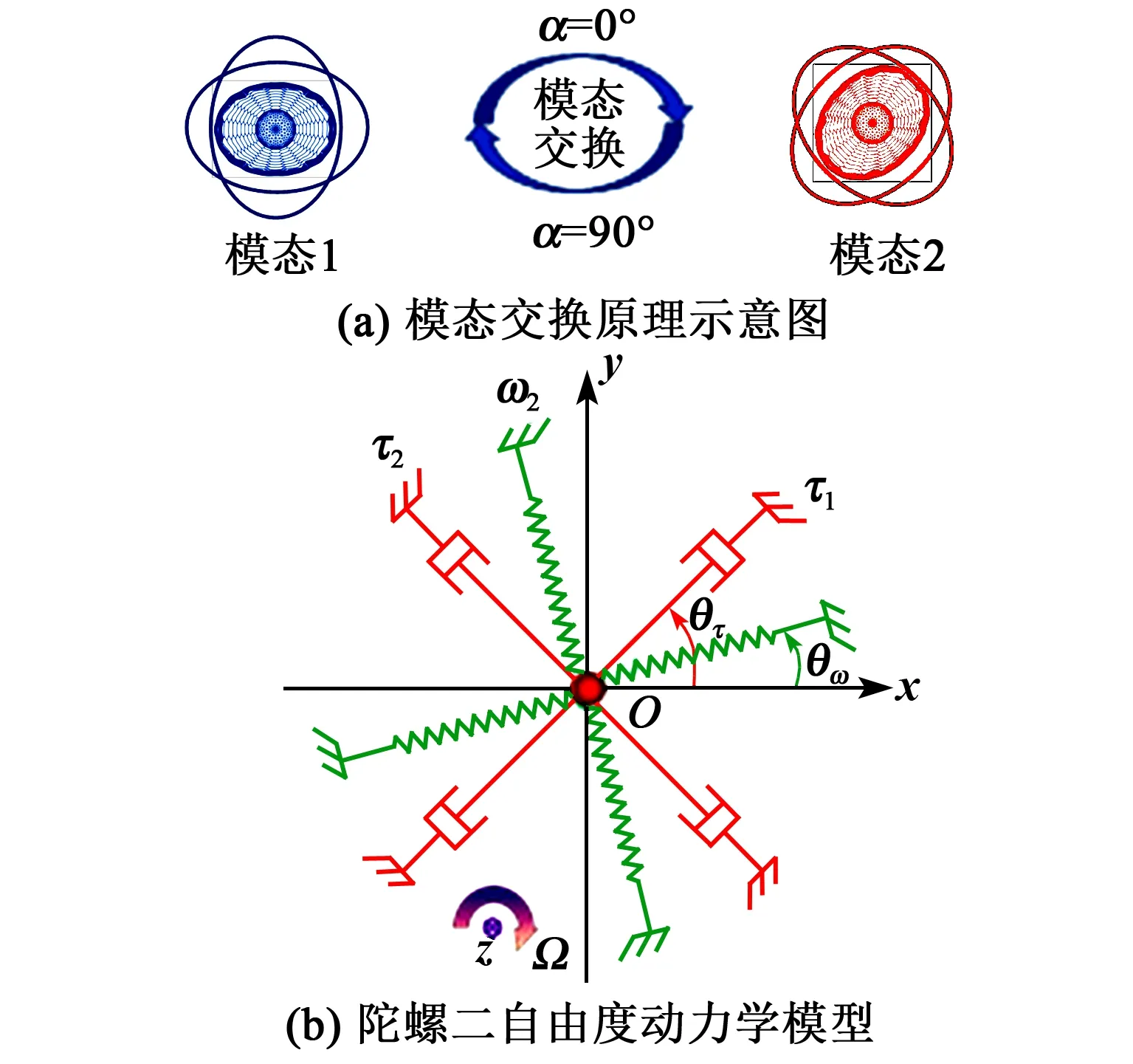
图3 模态交换与二自由度动力学模型示意图

Ωout(α)=Ω-Bsin2(α-θτ)

(1)

式中:Ω为外界角速度输入;B为陀螺零偏;α为驱动角;θτ为阻尼角。

如图3(a)所示,模态交换技术通过将陀螺的驱动角在0°和90°进行周期性切换,从而实现对陀螺零偏漂移的自校准。在控制系统中,通过切换虚拟开关实现对陀螺驱动控制环路和力平衡控制环路的切换,从而实现驱动角在0°与90°间的切换[14]。如图4所示,陀螺在驱动角为0°、90°时,输出可表示为

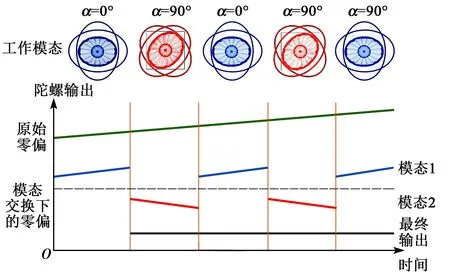
图4 模态交换技术抑制零偏漂移原理示意图

Ωout(0°)=ΩiecosLcosφ+Bsin2θτ

(2)

Ωout(90°)=ΩiecosLcosφ-Bsin2θτ

(3)

式中:Ωie为地球的自转速率;L为当地纬度;φ为方位角。

将式(2)与式(3)相加,可得到消除漂移后的陀螺输出为

G=Ωout(0°)+Ωout(90°)=2ΩiecosLcosφ

(4)

经过自校准后,该输出可用于进行寻北解算。基于模态交换技术,可以将陀螺的长期零偏稳定性、零偏重复性提升到较好水平,为寻北仪的寻北精度提供了技术保障。

2 滤波器设计

2.1 噪声成分分析

Allan方差曲线可对陀螺输出的噪声源进行分离和辨识,典型的微机电陀螺噪声成分一般包括角度随机游走、零偏不稳定性、量化噪声、速率随机游走及速率斜坡,如图5所示。模态交换技术可通过自校准对速率随机游走、速率斜坡过程进行有效抑制,从而提升陀螺的长期稳定性。

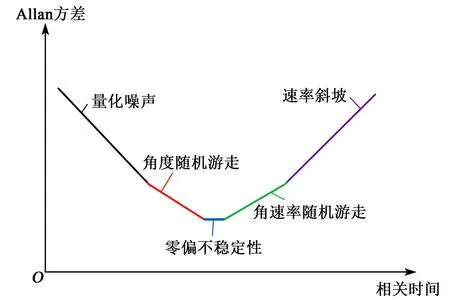
图5 微机电陀螺Allan方差曲线示意图

图6为本文选用陀螺的长时间测试Allan方差曲线。

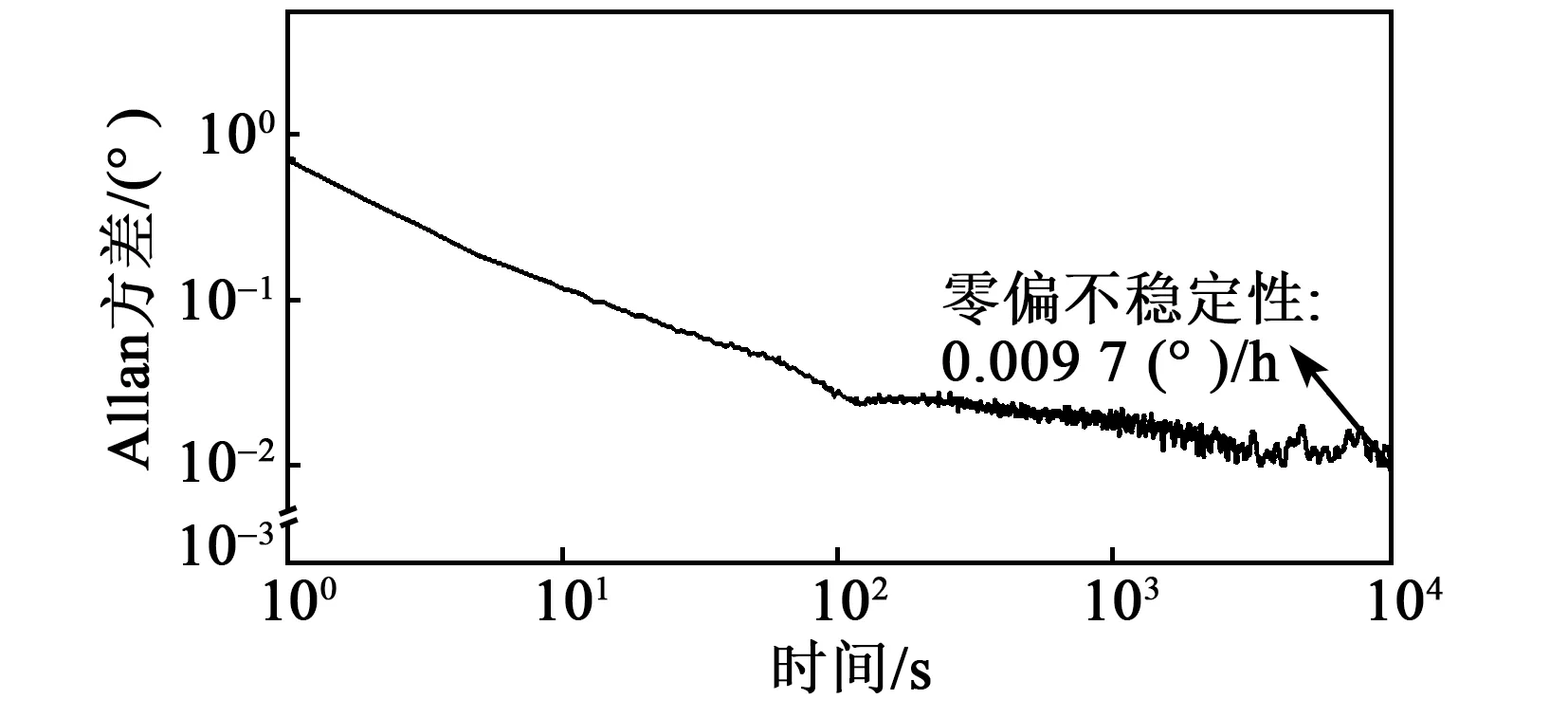
图6 蜂巢式微机电陀螺长时间测试Allan方差曲线

由图6可看出,对应陀螺输出频谱可近似将陀螺的噪声组成近似分为低频闪烁噪声(即1/f噪声)和白噪声。

如图7所示,陀螺输出的白噪声决定了角度随机游走,即陀螺达到指定精度所需的平均时间。而1/f噪声决定了陀螺的性能极限,即零偏不稳定性。1/f噪声仅存在于0～1 kHz低频域段,其来源于晶体管器件,仅由工艺与面积决定,无法避免。其在时域上表现为均值波动,故无法通过延长平均时间抑制。假设标定后不考虑陀螺零偏置的影响,则可将陀螺输出表示为

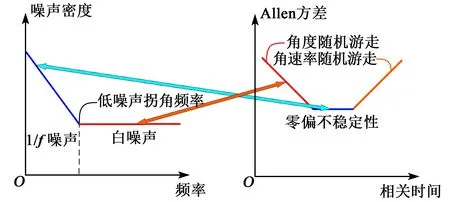
图7 陀螺Allan方差与陀螺输出噪声频谱对应关系示意图

G=Ωc+N0+Nf

(5)

式中:Ωc为陀螺仪敏感到地球自转的角速率输出真值;N0为由于陀螺白噪声导致的输出误差;Nf为陀螺1/f噪声导致的输出误差。通常Nf的存在限制了寻北的精度极限,而寻北时间长短可表示为抑制N0误差所需采样时间。

2.2 卡尔曼滤波

如图8所示,陀螺在模态一和模态二的输出通过模态交换时序控制单元处理后,得到可用于寻北解算的陀螺输出。对于给定位置的寻北仪,Ωc是确定的常值,这意味着对于寻北应用,快速而准确地得到G是平衡寻北精度和寻北时间的关键。本文基于上述理论,建立用于卡尔曼滤波的系统噪声模型,对陀螺输出白噪声进行实时抑制。

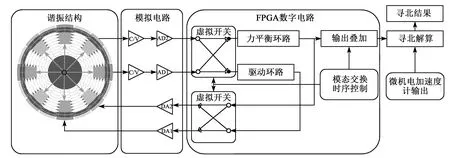
图8 模态交换技术控制陀螺输出用于寻北解算示意图

如图9所示,首先对陀螺输出G建立其离散系统状态方程:

(6)

式中:A,H均为一维单位向量;z(k)为一维测量输出向量;w(k)为一维随机过程噪声;v(k)为一维随机测量噪声。

以一定时间平滑后陀螺输出G′作为时间序列主趋势的基准,对系统噪声模型进行定量,考虑到对滤波效果和陀螺输出动态的要求,本文取平滑时间为100 s。由式(5)可知,对于平滑后的输出G′有:

G′=Ωc+N′0+Nf

(7)

式中N′0为100 s平滑后陀螺白噪声导致的输出误差。

由式(5)、(7)可得:

G-G′=N0-N′0=v

(8)

将平滑后滤去的噪声定义为测量噪声v(k)。对于G′中的剩余白噪声定义为过程噪声w(k),则:

w=N′0

(9)

对确定后的系统状态方程模型转化为卡尔曼滤波模型,卡尔曼滤波过程如下:

(10)

(11)

(12)

(13)

P(k,k)=[I-K(k)H(k)]P(k,k-1)

(14)

3 实验结果与讨论

为验证上述卡尔曼滤波对于寻北应用的效果,本文对滤波前后的陀螺输出进行了测试,图10为陀螺1 Hz采样率采得的数据。滤波后的噪声水平明显下降,其主趋势与100 s平滑后的数据时域对齐后的差值如图11所示,满足本文允许引入的误差ε范围。

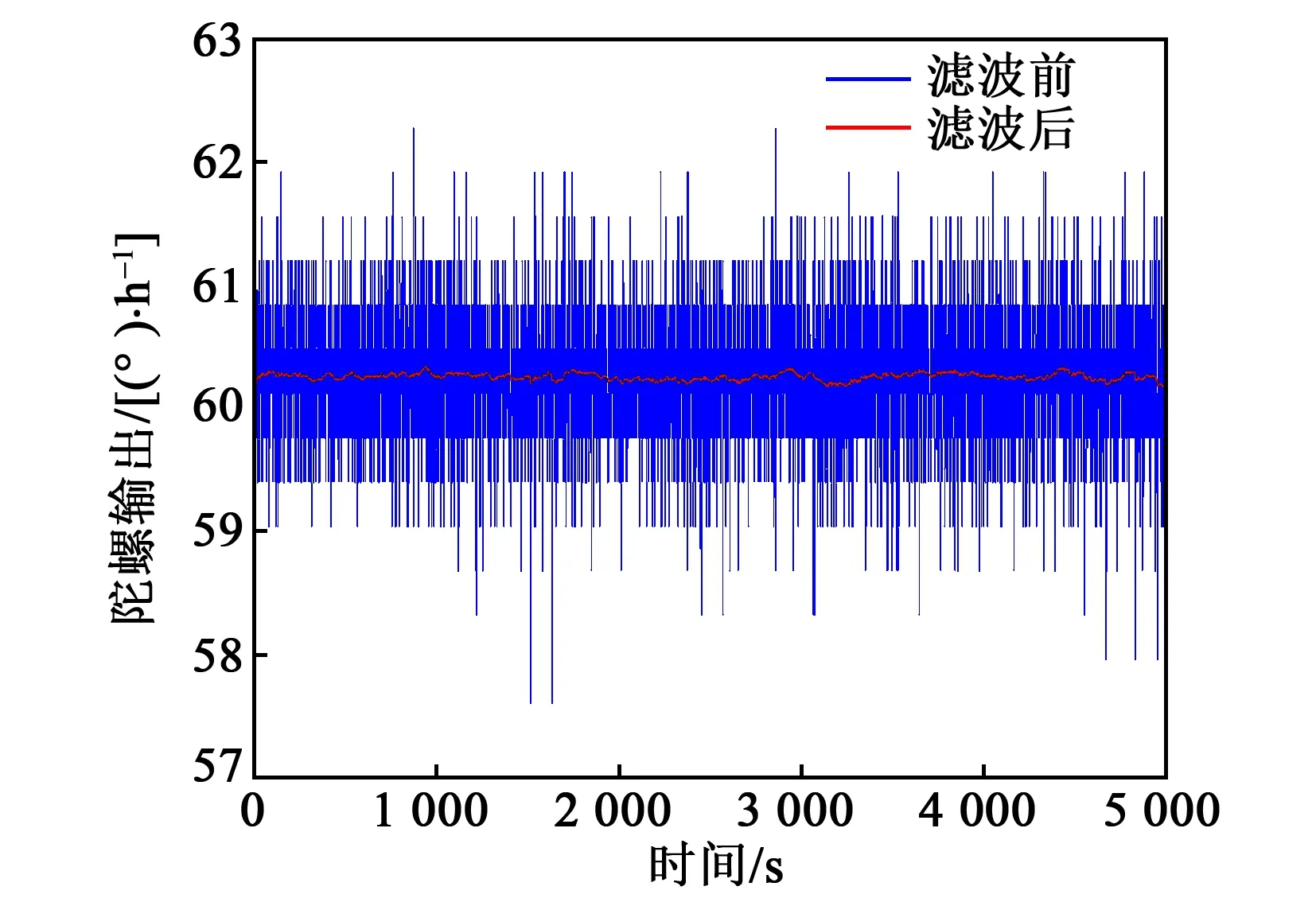
图10 滤波前后陀螺输出对比图

图11 滤波后与滤波前100 s平滑输出差值图

对滤波后的噪声成分及特性进行了实验验证。如图12所示,对陀螺滤波前后的输出进行频域分析,数据采样率为200 Hz。由图可见,陀螺滤波后白噪声得到明显抑制。滤波前后的Allan方差曲线如图13所示。由图可看出,滤波对于相关时间100 s前噪声进行重组,降低了相关时间100 s前的噪声。对于寻北应用,即是可使用更短的寻北时间获得与原来相匹配的寻北精度。而由于滤波后陀螺动态性能被压缩,滤波后寻北时间将与滤波器设定的初值收敛时间相关。因此,滤波后1 s的采样数据与滤波前100 s的采样数据达到相同的寻北精度。

图12 滤波前后陀螺输出频谱图

图13 滤波前后Allan方差曲线图

4 结束语

本文针对基于模态交换工作模式下的蜂巢式微机陀螺进行了卡尔曼滤波设计。对于蜂巢式微机电陀螺的输出噪声进行了建模分析,采用噪声分离的手段定量建立卡尔曼滤波模型,并进行了实验验证。结果表明,本文得到的卡尔曼滤波模型可在不降低寻北精度的前提下有效地缩短本文寻北仪的寻北时间,对于惯性寻北领域具有重要意义。