基于相关峰检测的π/4－DQPSK 频差估计*

魏 鹏，陆锐敏，谢世珺

(总参第六十三研究所，南京 210007)

1 引言

π/4－DQPSK 因其比QPSK 更小的包络波动、更高的频率效率及无需载波同步的差分解调算法在移动通信和卫星数字通信等领域中得到了广泛的应用［1］，但是其差分解调性能会因相对符号速率较大的频差而迅速恶化，也即一定的频差对低速(相对频差而言)π/4－DQPSK 差分解调性能影响更大，因而对其频差进行估计是非常必要的。

目前常用的频差估计方法可分为基于快速傅里叶变换(Fast Fourier Transform，FFT)算法的频域估计算法和基于自相关函数的时域估计算法。频域估计算法的基本思路是将接收到的调制信号转换为单音信号，再进行2 的幂次方点数的FFT，最后搜索峰值并计算频差，这类算法运算量不大，精度高，可以实时实现，但频差估计精度受FFT“栅栏”效应影响较大。为此，Rife 算法［2］、插值FFT 算法［3－4］、加窗FFT 算法等多种改进方法被提出，但这些方法都是以运算量的增加来换取频率估计精度的提高。基于自相关函数的频差估计算法主要有Kay 估计［5］、Fiz估计［6］及L＆R 估计［7］等算法，这类算法中接收机根据发送的已知复M 序列，在本地产生一个共轭序列，与接收到的M 序列进行相关运算，得到一个去除了调制信息的单音信号，然后对这个单音信号进行不同延迟的相关、加权及求反正切运算得到频差的估计值。这类算法必须首先完成位同步和帧同步，且Fitz 算法和L＆R 估计算法估计范围及精度与采用自相关运算分支数N 有关，Fitz 估计的归一化频率范围为，L＆R 估计的归一化频率范围为，其中R 为AD 采样倍数，N 为小于复M序列长度的正整数，N 越大，估计精度越高，估计范围越小。此外，文献［8］提出了一种基于自回归(Auto Regressive，AR)模型、FFT 和二阶锁相环相结合的GMSK 信号频差捕获和跟踪方法，具有频差估计范围大、精度高且不需要首先完成帧同步的优点，但三种方法的结合无疑使得系统结构更加复杂，运算量大增。

本文结合无线通信系统中常用M 序列进行信道估计和各种同步的实际情况，提出了一种基于相关峰检测的频差估计方法，该频差估计方法可与位同步、帧同步同时实现，用较小的代价将频差控制在π/4－DQPSK 解调所允许的频差范围之内。

2 基于相关峰检测的频差估计原理

图1 所示为基于相关峰检测的频差估计原理框图。接收信号为带有频差的基带信号，不考虑噪声的影响，则接收信号可记为

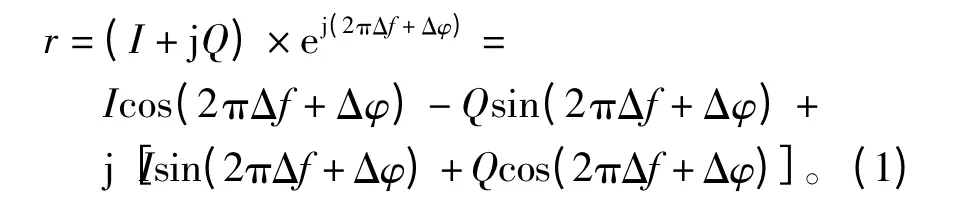
式(1)中的实部和虚部分别对应图1 中的I 和Q，Δf 和Δφ 分别为频差和相差。这两路基带信号经过AD 采样、匹配滤波、差分解调后得到两路包含M 序列的抽样前信号ck和dk。若没有频差，抽样判决后可得到发送序列，但较大频差存在的情况下可能导致抽样判决出错或性能下降。

图1 基于相关峰检测的频差估计算法原理框图Fig.1 The frequency offset estimation diagram based on correlation peak detection

将ck和dk分别进行相关检测，当接收信号与本地M 序列完全匹配时有

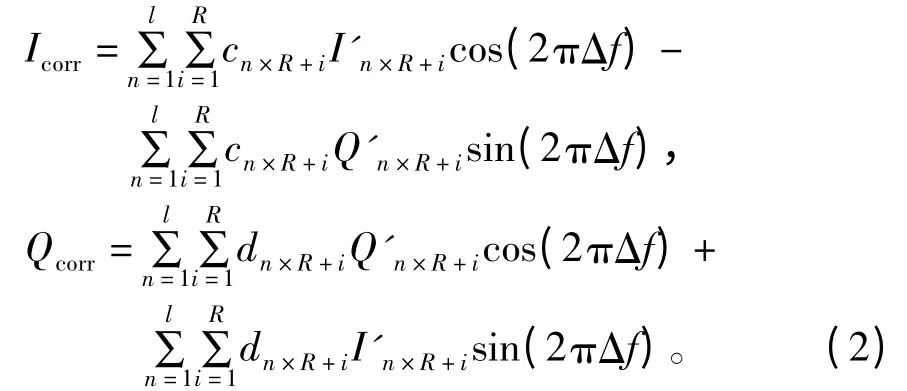
式中，Icorr和Qcorr分别表示I 路和Q 路的相关峰值;I'和Q'表示本地的I、Q 两路M 序列，其值均为1 或－1;l 表示M 序列长度;R 表示每符号AD 采样倍数。当I 路信号与Q 路信号所采用的M 序列不相关时，式(2)中的后一项由于接收信号与本地M 序列不相关，从而可以忽略，而前一项随着频差Δf 的增大而减小(一定范围内)，无法从中获取频差信息;而当I 路信号与Q 路信号所采用的M 序列相同时有In×l+i=Qn×l+i，cn×R+i=dn×R+i。则式(3)可简化为

将式(3)中的Icorr与Qcorr相除得

将式(3)中的Icorr与Qcorr求平方和得

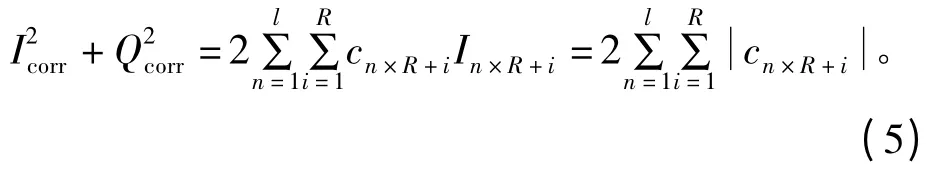
式(4)仅包含频差信息，式(5)是不受频差影响的I 路和Q 路相关峰值的平方和，因此可根据式(5)首先检测到相关峰出现的位置，然后根据式(4)计算频偏。由式(4)可知，该算法的估计范围为

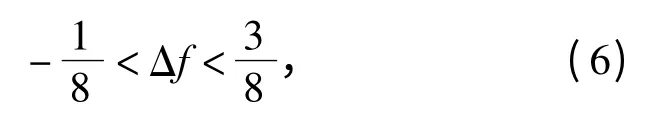
即频差估计范围在符号速率的－1/8～3/8 之间，用采样频率fs作为归一化频率，R 为采样倍数，则

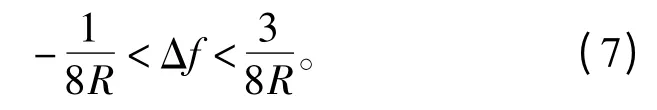
当不存在频差时，I 与Q 路检测出的峰值接近，随着频差的增大，一路的峰值减小，另一路的峰值增大，但其平方和基本保持不变。

3 基于相关峰检测的频差估计算法仿真

采用Matalab 对本文提出的基于相关峰检测的频差估计算法进行仿真，将其频差估计范围和精度与传统的Kay 估计、Fitz 估计、L＆R 估计进行定量对比。考虑到实际通信系统中用于信道估计或同步所支持的实际M 序列不宜过长，如每秒16 000跳，信道2.56 Mb/s，采用π/4－DQPSK 调制的跳频通信系统中，每跳可传输80个符号(160 b)，仿真中设置M 序列长度为104 b，I、Q 两路包含相同的52 b M 序列，其余比特用来传输如时间信息、跳频密钥等其他同步信息。显而易见，M 序列的长度越长，相关峰值受噪声影响越小，频差估计精度越高，但更长的M序列也意味着传输效率的降低和运算量的增加。I、Q 两路信号经π/4－DQPSK 调制，内插(R=12)和成型滤波之后加入频偏和高斯白噪声。接收端使用不同的频差估计算法对频差进行估计，其中，Fitz 估计和L＆R 估计的相关分支数N=1，保证其足够的估计范围。

3.1 基于相关峰检测的频差估计范围仿真

图2 所示为基于相关峰检测算法的频差估计范围仿真结果。仿真中设置800个频差，取值为Δf=，N 在－400～400 之间取值。由仿真结果可见，在横轴对应的－100 和32 点，即频差约为－0.01，之间的频差可得到正确的估计，频差超出此范围时，估计出错，此结果与式(8)的理论推导一致。

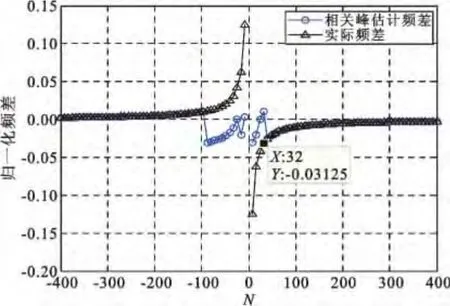
图2 相关峰检测算法频差估计范围Fig.2 The frequency offset estimation rang based on correlation peak detection

3.2 基于相关峰检测的频差估计精度仿真

为全面评估基于相关峰检测的频差估计精度，在其频差估计范围内取3个不同量级的归一化频差0.03、0.005 和0.0004 进行仿真。

图3 和图4 所示为频差Δf=0.03 时相关峰估计算法与Kay 估计、Fitz 估计、L＆R 估计的仿真对比。由仿真结果可知，相关峰估计能够较准确地估计出频差，当信噪比Eb/N0在0 dB以上时，均方误差小于2 ×10－4;而其他三种估计因频差超出了其估计范围不能对频差进行正确估计，均方误差超出图4 显示范围。此仿真结果并不能说明相关峰估计的范围更大，当AD 采样倍数R=12 时，相关峰估计的范围为－0.01～0.03，其他三种估计的范围为－0.02～0.02，因而其估计范围相当。

图3 频差估计精度比对(Δf=0.03)Fig.3 Comparison of frequency offset estimation precision when Δf=0.03

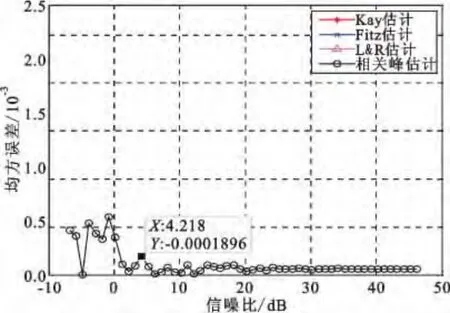
图4 频差估计均方误差比对(Δf=0.03)Fig.4 Comparison of frequency offset estimation MSE when Δf=0.03

图5 和图6 所示为频差Δf=0.005 时相关峰估计算法与Kay 估计、Fitz 估计、L＆R 估计的仿真对比。由仿真结果可知，四种估计方法的精度接近，当信噪比在0 dB以上时，均方误差均小于2 ×10－4。

图5 频差估计精度比对(Δf=0.005)Fig.5 Comparison of frequency offset estimation precision when Δf=0.005

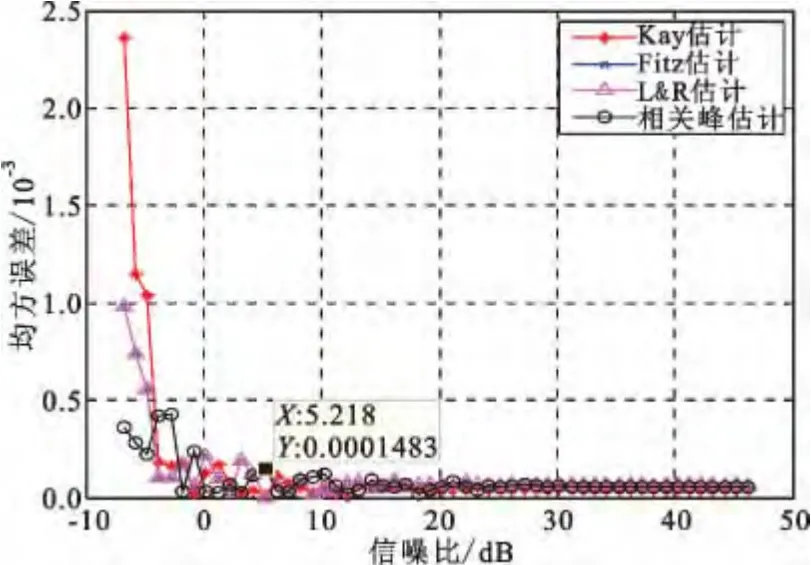
图6 频差估计均方误差比对(Δf=0.005)Fig.6 Comparison of frequency offset estimation MSE when Δf=0.005

图7 和图8 所示为频差Δf=0.000 4 时相关峰估计算法与Kay 估计、Fitz 估计、L＆R 估计的仿真对比。由仿真结果可知，相关峰估计的精度略差于其他三种估计，但仍能满足当信噪比在0 dB以上时均方误差均小于2 ×10－4。

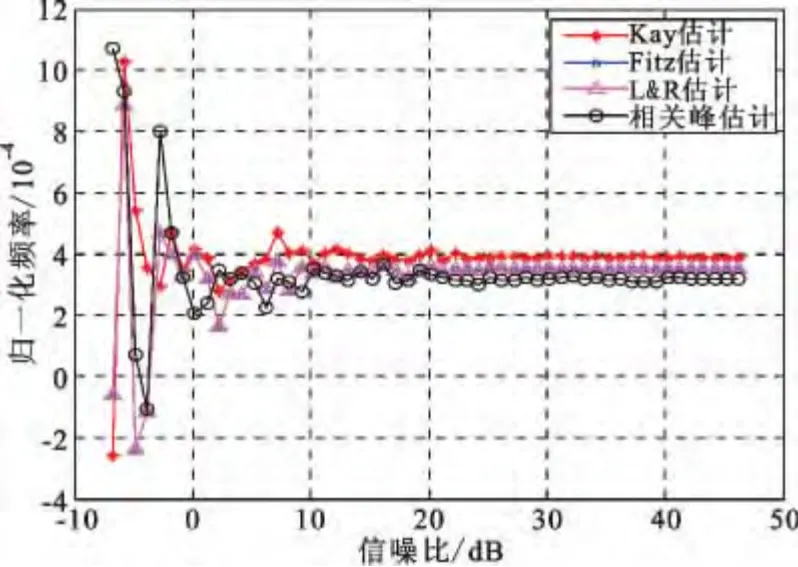
图7 频差估计精度比对(Δf=0.000 4)Fig.7 Comparison of frequency offset estimation precision when Δf=0.000 4

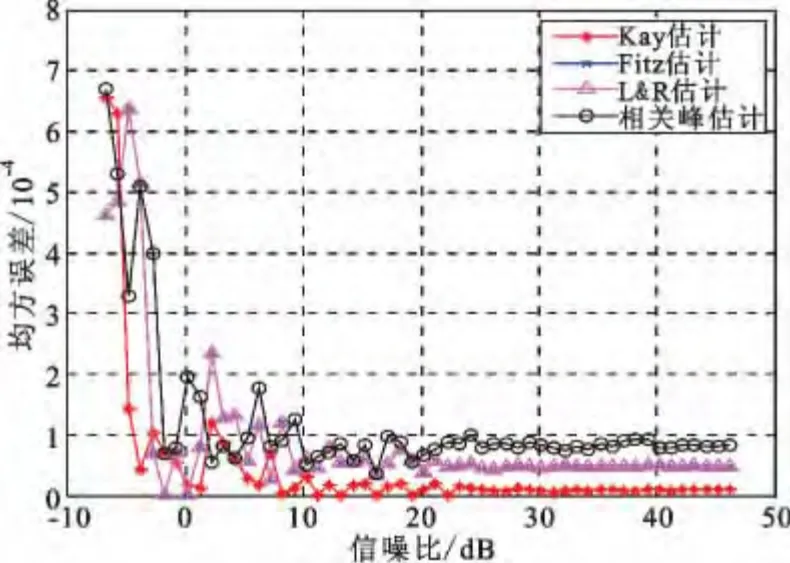
图8 频差估计均方误差比对(Δf=0.000 4)Fig.8 Comparison of frequency offset estimation MSE when Δf=0.000 4

由本节仿真结果可知，在频差较小的情况下，相关峰估计的频差估计精度不及Kay 估计、Fitz 估计及L＆R 估计等经典估计算法，但其估计误差能够保证在信噪比0 dB以上小于2 ×10－4，那么此精度能否满足π/4－DQPSK 解调性能的要求呢?为此，下面对频差对π/4－DQPSK 差分解调性能影响进行仿真。

3.3 频差对π/4－DQPSK 解调性能影响仿真

仿真设置中的内插倍数、成型滤波参数设置不变，将仿真数据的长度设为160 000个，分别引入归一化频差为0.001 5、0.001 3、0.001 1、0.000 9、0.000 7、0.000 5。由图9 仿真结果可知，当归一化频差在0.000 5 时已完全不影响解调性能，因而当估计误差小于2 × 10－4时完全能够满足π/4－DQPSK 解调性能的要求。

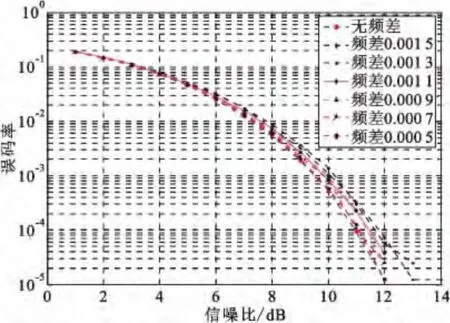
图9 频差对π/4－DQPSK 解调性能的影响Fig.9 The influence of frequency offset on π/4－DQPSK demodulation performance

3.4 运算量比较

设M 序列的长度为L，则Kay 估计、Fitz 估计、L＆R 估计需要在完成位同步和帧同步之后将M 序列的调制信号与本地M 序列经相同调制后的共轭进行复数乘得到包含频差的单音信号，这需要进行L 次复数乘;对Kay 估计，需要事先计算一组加权系数，其个数为L，然后将包含频差的单音信号与其共轭延迟(延迟1 符号)进行复数乘，对所得结果的实部、虚部之比求反正切，并对L个反正切进行加权平均得到频差的估计值，因此还需要L 次复数乘、L 次实数除(可等同实数乘)、L 次求反正切、1 次加权平均(L 次实数乘和1 次实数除);对Fiz 估计，其自相关分支数N=1 时，则需要将包含频差的单音信号与其共轭延迟(延迟1 符号)进行复数乘，并将结果求和，计算实部与虚部比值的反正切后除以其求和的个数得到频差的估计值，因此需要L 次复数乘、1次L个复数求和(等于2L 次实数加)、1 次求反正切及1 次除法。当其自相关分支数据为N ＞1 时，其运算量为1 时的N 倍;对L＆R 估计的运算量与Fitz估计相当。基于相关峰估计算法可以将频差检测与位同步、帧同步同时完成，对差分解调后的I、Q 两路信号进行相关峰检测，则一个采样时钟内需计算2LR 次实数加。若假设相关峰法已经首先完成了位同步和帧同步，则其2LR 次加法只需在LR个采样时钟内完成即可。几种频差估计算法的运算量比较见表1。

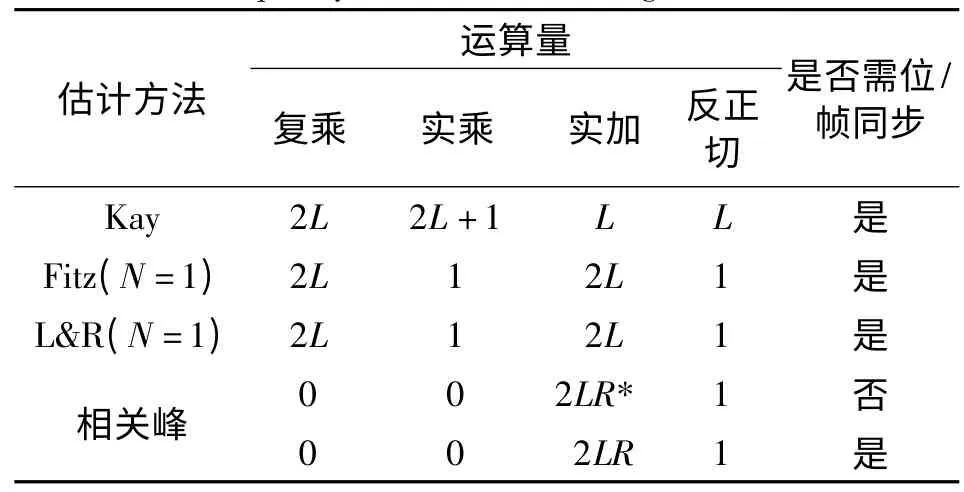
表1 几种频差估计算法的运算量比较Table 1 Computational complexity comparison among several frequency offset estimation algorithms

由表1 可见，相比于其他三种估计方法，基于相关峰的频差估计算法无需进行消耗硬件资源较多的乘法运算，非常适合于在FPGA、DSP 等可编程器件中实现。

4 结束语

针对低速π/4－DQPSK 差分解调性能受频差影响较大的问题，本文提出了一种基于相关峰检测算法的频差估计算法。该算法在I、Q 两路发送的M码序列相同的条件下，根据I、Q 两路信号的相关峰值求得频差，而无需像其他估计方法那样首先去除调制信息，恢复只包含频差信息的单音信号后再进行频差估计。数值仿真结果表明其估计范围与Kay估计、Fitz 估计及L＆R 估计等经典估计算法相当(Fitz 估计和L＆R 估计在相关分支数N=1 时)，估计精度略差，但在其估计范围内估计的均方误差均小于2 ×10－4，能够满足π/4－DQPSK 差分解调时频差小于0.000 5 的要求。此外，该算法具有结构简单(只需对差分解调结果进行相关运算)、运算量小(只需加法运算)且不需要首先完成位同步和帧同步的优点，非常有利于系统实现。不足之处在于本文提出的频差估计方法根据π/4－DQPSK 差分解调导出，后续应对其是否能应用于其他调制方式做进一步研究。

［1］刘聪锋.高效数字调制技术及其应用［M］.北京:人民邮电出版社，2006.LIU Congfeng.Efficient Digital Modulation Technirue and Its Application［M］.Beijing:People's Posts and Telecommunication Press，2006.(in Chinese)

［2］Rife D C，Boorstyn R R.Single－Tone Parameter Estimation from Discrete－Time Observations［J］.IEEE Transactions on Information Theory，1974，20(5):591－598.

［3］Aboutanios E，Mulgrew B.Iterative Frequency Estimation by Interpolation on Fourier Coefficiens［J］.IEEE Transactions on Signal Processing，2005，53(4):1237－1242.

［4］龚超，张邦宁，郭道省.基于FFT 的快速高精度载波联合参数估计算法［J］.电子学报，2010，38 (4):766－770.GONG Chao，ZHANG Bangning，GUO Daoxing.A Quick and Accurate Union Carrier Parameter Estimation Algrithm Based on FFT［J］.Acta Electronica Sinica，2010，38(4):766－770.(in Chinese)

［5］Kay S.A fast and Accurate Single Frequency Estimator［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1989，37(12):1987－1990.

［6］Fiz M P.Further Results in the FastEstimation of a Single Frequency［J］.IEEE Transactions on Communications，1994，42(2/3/4):862－864.

［7］Lovell B C，Williamson R C.The statistical performance of some instantaneous frequency estimators［J］.IEEE Transactions on Signal Processing，1992，40(7):1708－1723.

［8］吴团锋，徐友云，归琳，等.Turbo 编码GMSK 信号的多普勒频移捕获与跟踪［J］.电讯技术，2011，51(8):61－65.WU Tuanfeng，XU Youyun，GUI Lin，et al.Doppler Frequency Shift Acquisition and Tracking for Turbo Coded GMSK Signals［J］.Telecommunication Engineering，2011，51(8):61－65.(in Chinese)