新型弹性侧支撑长轨枕式减振轨道结构力学特性研究

曹子勇,和振兴,苏 程,包能能,王玉魁,贠剑峰

(兰州交通大学 机电工程学院,兰州 730070)

城市轨道交通引起的振动和噪声问题日益凸显[1-2],在新建线路上采用了大量不同减振等级的减振轨道,缓解列车通过时引起的振动和噪声影响。目前既有轨枕式减振轨道[3]均采用枕下支撑方式,将减振部件(弹性垫板)放置在轨枕下方,利用弹性材料的压缩变形实现减振效果,但存在弹性部件难以更换和减振能力不足的缺陷。因此,研究团队提出改变轨枕的支撑方式,由底部支撑变为侧部支撑,利用弹性侧支撑垫的剪切变形为轨道系统提供弹性的新结构。

对于既有轨枕式减振轨道,相关学者已开展大量研究。文献[4]对弹性长轨枕进行模态分析,得出合理的结构参数,并对三种减振型轨枕的稳定性能作对比分析,发现弹性长轨枕的结构最优;文献[5]对弹性长轨枕进行垂向受力分析,通过改变枕长和支撑长度的结构参数,计算了长枕轨下和枕中的弯矩值,得出以0.4作为弹性长轨枕枕长与支撑长度的合理比例关系;文献[6]提出了一种新型的弹性侧支撑式减振轨道减振频率调制装置,采用理论研究和试验测试结合的方法,详细研究了弹性侧支撑式减振轨道的力学特性,并通过落锤试验验证了理论研究,证明安装减振频率调制装置可以显著减小轨道的振动。文献[7]研究了在轮轨粗糙度激励下梯形轨枕轨道的振动特性,通过与普通轨道对比,得到梯形轨枕轨道具有更好的减振能力;文献[8]利用车辆—轨道耦合分析方法,分析列车高速通过时轨道系统的动力响应,进行CRTS Ⅲ型板式无砟轨道减振垫层的动力影响及结构优化研究。

针对不同路段下的基础道床配筋而言,相关学者也进行了大量研究。文献[9]提出了一种新型连块式轨枕,通过现场应用发现,桥梁和路基的道床板更易发生开裂,而隧道内的道床板不易产生开裂,并由裂缝限值控制裂缝宽度;文献[10]采用不同的荷载组合方式和容许应力法,对钢筋桁架轨枕式整体道床进行配筋设计,结果表明,基础变形对配筋的影响较为显著,而温度力的影响相对较小;文献[11]建立了CRTS Ⅲ型板式无砟轨道的有限元模型,采用极限状态法对复合道床板进行配筋设计,通过理论优化计算后,轨道板配筋可节约18.4%,复合道床板整体配筋可节约4.4%。

弹性垫板在减振轨道中起着关键的作用,能够有效缓冲车辆通过路轨时产生的振动和冲击,对路基和轨枕起一定的保护作用。文献[12-13]建立了网孔式弹性垫板三维有限元模型,研究了网孔式弹性垫板动刚度和阻尼系数的温变特性,得出温度低于-10 ℃时,弹性垫板的动刚度和阻尼系数随温度降低而急剧增大。

文献[14]通过改进的理论计算方法和性能试验研究了不同水平剪切变形状态下的竖向压缩刚度,结果表明理论计算与试验结果较吻合。文献[15]将Haringx柱模型[16]简化为仅包含剪切刚度与转动刚度的双弹簧模型,研究了轴向载荷对弹性支座动刚度、阻尼系数和高度折减的影响,为支座在轴向载荷作用下的响应分析[17-18]提供了依据。文献[19-20]提出了一种正六边形蜂窝状结构的弹性垫板,研究了网孔壁厚和网孔孔径等关键参数对其静/动刚度的影响,并将网孔式弹性垫板和传统沟槽型弹性垫板作对比研究。

为了解决弹性部件更换困难和减振能力不足的问题,和振兴提出了一种新型侧支撑无砟轨道结构[21],在该结构中,侧支撑式弹性垫板会在轨枕受到外部载荷时发生剪切和压缩组合变形。由于轨道结构特殊,本文以新型弹性侧支撑长轨枕式减振轨道为研究对象。首先,在轮载作用下,找出弹性侧支撑长轨枕式减振轨道和既有轨枕式减振轨道道床最不利的位置及应力集中区域,对比分析载荷施加在弹性侧支撑长轨枕式减振轨道轨枕中上方和轨枕正中位置的部件应力分布。其次,对两种减振轨道的整体道床进行配筋设计和检算;最后,采用试验验证有限元模型计算的准确性,通过有限元计算,研究侧支撑式弹性垫板的厚度、空间倾斜量和材料硬度对轨枕节点动刚度和垂向最大位移的影响规律。

1 减振轨道结构及有限元模型

新型弹性侧支撑长轨枕式减振轨道结构如图1所示,由道床、侧支撑式弹性垫板和轨枕等组成。轨枕采用侧面支撑方式,支撑面在的圆锥面上截取,圆心在轨枕纵向中心延长线位置,限制了轨枕的横向位移,圆弧半径为R;侧支撑式弹性垫板以上表面为基准偏移δ角度,得到空间倾斜量x。侧支撑式弹性垫板可以更换,轨枕与侧支撑式弹性垫板之间采用燕尾槽连接,两者紧密连接,不易脱落;中心水沟解决了积水问题;可采用轨道单元预制现场拼装施工或轨排现场组装,道床现浇的方法施工;整体道床两侧采用通透式,可以节省混凝土材料。对于弹性部件的更换问题,以上结构设计更易将轨枕与侧支撑式弹性垫板从承轨槽中取出并更换。

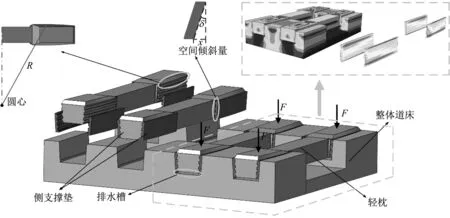
图1 新型弹性侧支撑长轨枕式减振轨道结构Fig.1 The new elastic side-supported long sleeper type damping track structure

由图1中的应力云图可见,大部分的振动能量被橡胶弹性减振垫板的变形所耗散,其余的振动能量则沿着两侧承轨槽的倾斜弧面传递,向两侧传递的振动波在纵向排列的轨枕间可抵消部分能量,减少了振动能量向基础的传递。

两种减振轨道的有限元模型,弹性垫板、轨枕和整体道床均采用六面体单元,如图2所示。两种减振轨道的结构参数对比,如表1所示。

表1 减振轨道结构参数对比Tab.1 Comparison of structure parameters of damping track

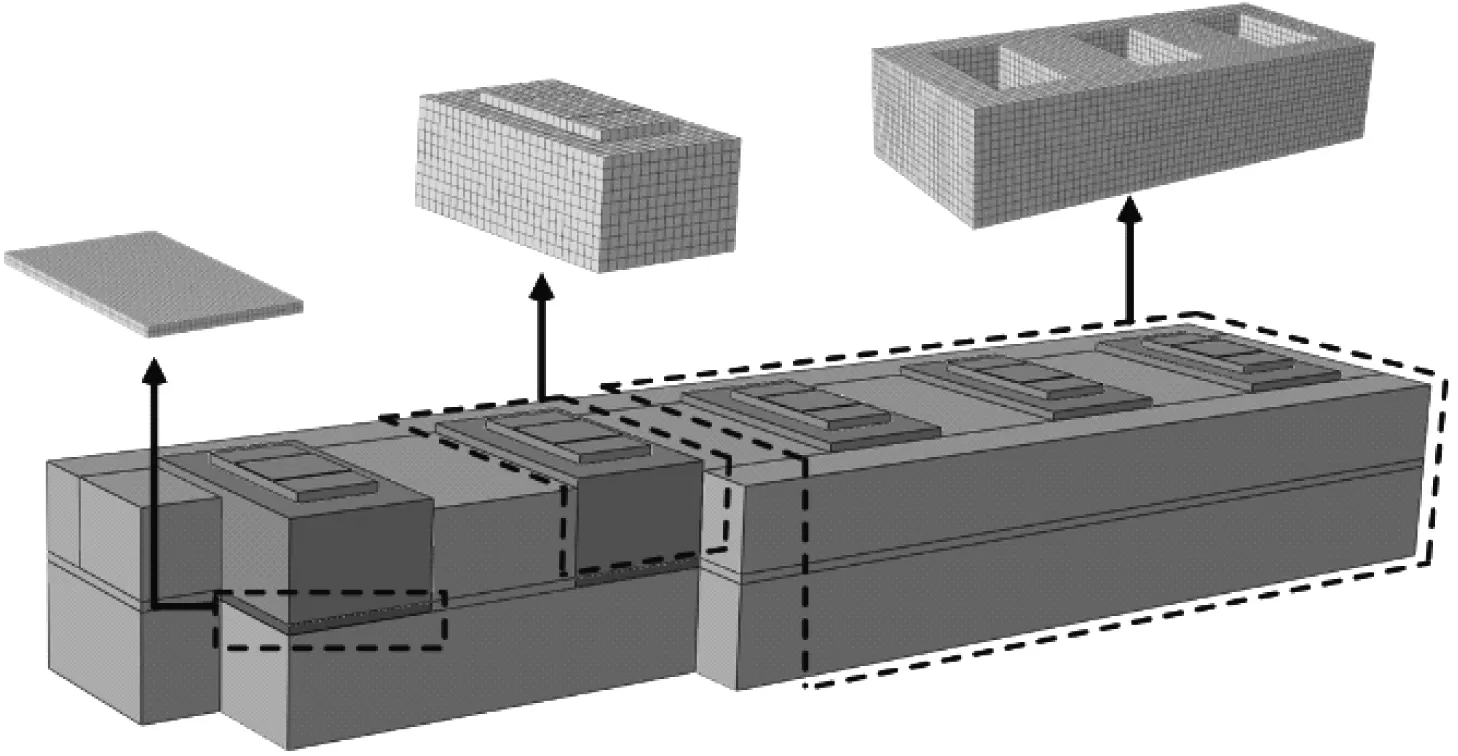
(a) 下支撑轨枕式减振轨道模型

2 应力分布与强度分析

研究在轮载作用下,整体道床的应力分布情况,将既有轨枕式减振轨道与弹性侧支撑式减振轨道进行对比,找出两种减振轨道的最不利位置和道床的应力集中区域。利用模型结构和受力分布的对称性,用模型的一半计算,并将扣件、钢轨和车轮简化。

2.1 减振轨道参数

图2中减振轨道模型主要由钢轨、扣件、轨枕、弹性垫板以及整体道床组成,上述结构或部件的具体材料参数如表2所示。既有轨枕式减振轨道整体道床尺寸为3 135 mm×800 mm×320 mm;弹性侧支撑式减振轨道整体道床尺寸为3 135 mm×650 mm×320 mm。

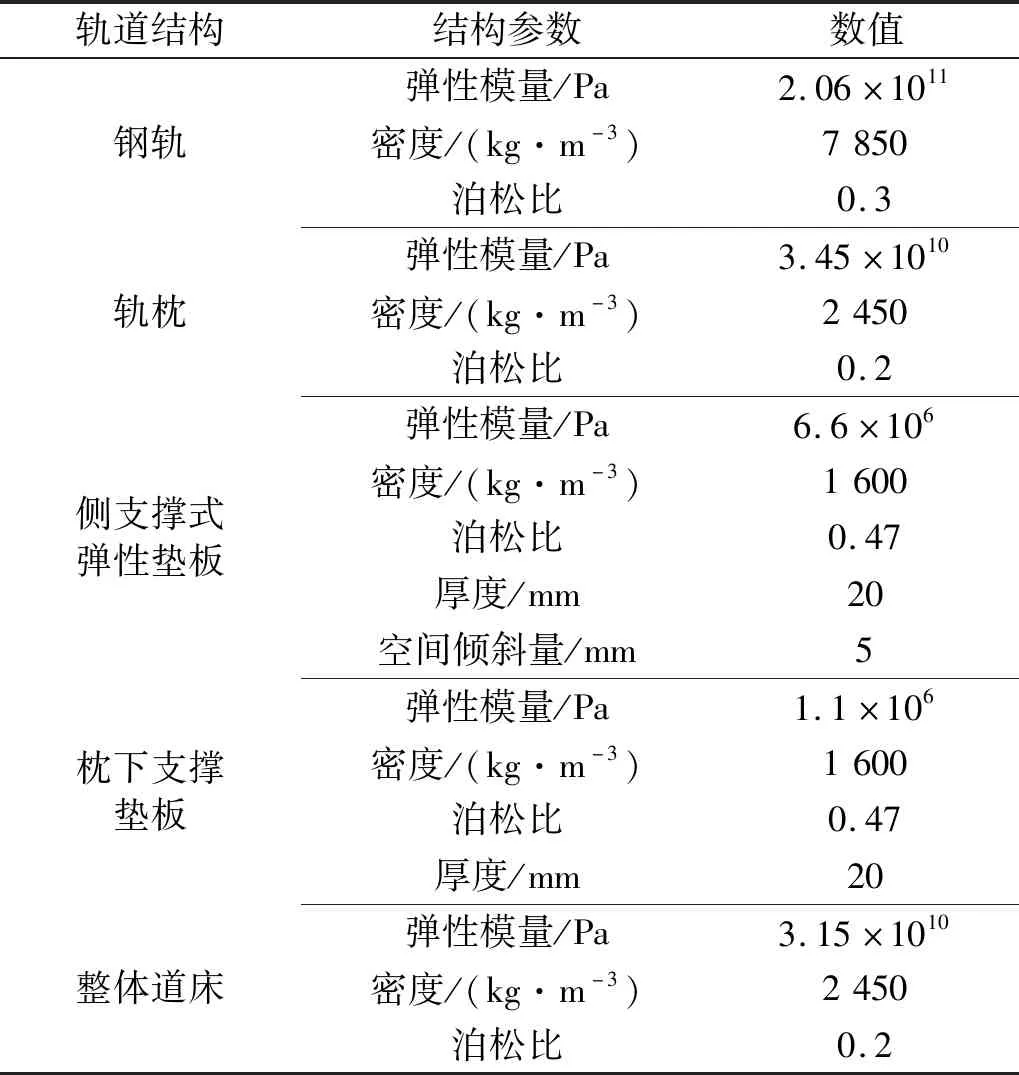
表2 减振轨道参数Tab.2 Damping track parameters

2.2 轮载作用下的应力分布

由于结构特殊,为了找到整体道床最不利的受力位置,从结构上来看,侧支撑式弹性垫板主要受到剪切的作用,弹性侧支撑式减振轨道整体道床可能出现应力集中的位置在承轨槽的支撑面上。枕下支撑垫板主要受到压缩作用,既有轨枕式减振轨道整体道床可能出现应力集中的位置在承轨槽底部。

在相同轮载作用下,为了保证两种减振轨道的钢轨垂向位移保持一致,枕下支撑垫板的弹性模量调至1.1×106Pa。考虑车轮和钢轨的自重,对车轮施加80 kN的垂直载荷,车轮与钢轨之间采用摩擦接触的连接方式,摩擦因数为0.15。Mises应力云图可清晰描述出整个模型中的应力变化情况及应力集中位置,因此,当车轮以20 km/h的速度通过时,得到弹性侧支撑轨枕式减振轨道和既有轨枕式减振轨道的Mises应力分布云图,如图3所示。

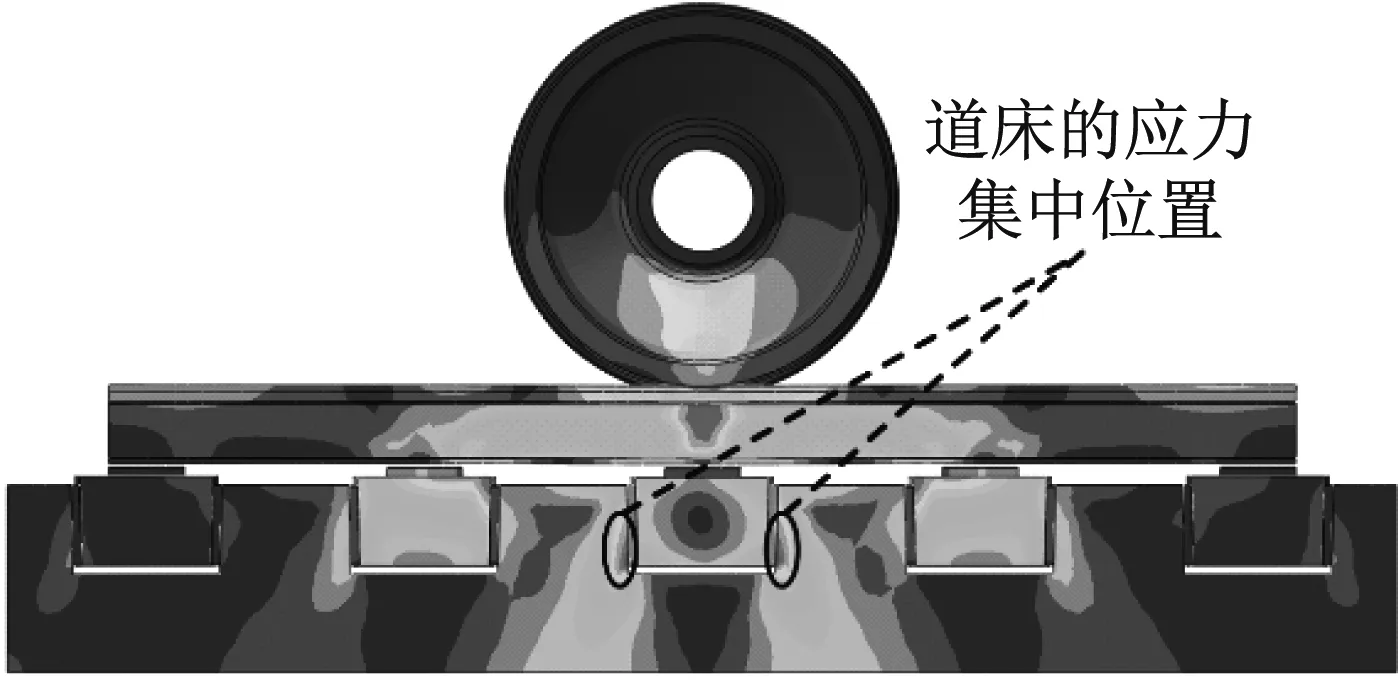
(a) 侧支撑轨枕式减振轨道的应力分布

由图3可知,车轮运行到整体道床中间位置时,整体道床的应力达到最大值,此时为整体道床的最不利位置。对于弹性侧支撑式减振轨道,道床承轨槽的折角处存在应力集中,对于既有轨枕式减振轨道,应力集中在承轨槽底部。两种减振轨道的应力分布较大的区域明显不同,既有轨枕式减振轨道整体道床应力分布区域较小,而弹性侧支撑式减振轨道基础道床应力集中在承轨槽两端的下支撑面上,应力分布区域较大,压力所产生的振动波向两侧相邻的纵向排列的轨枕间传递,由多根轨枕共同承担,并将部分能量相互抵消,可以延长轨道的整体寿命。

图4是两种减振轨道结构应力集中处应力随时间的变化规律,图4(a)为侧支撑轨枕式减振轨道道床在承轨槽折角处的应力曲线,图4(b)为下支撑轨枕式减振轨道道床在承轨槽底部的应力曲线。

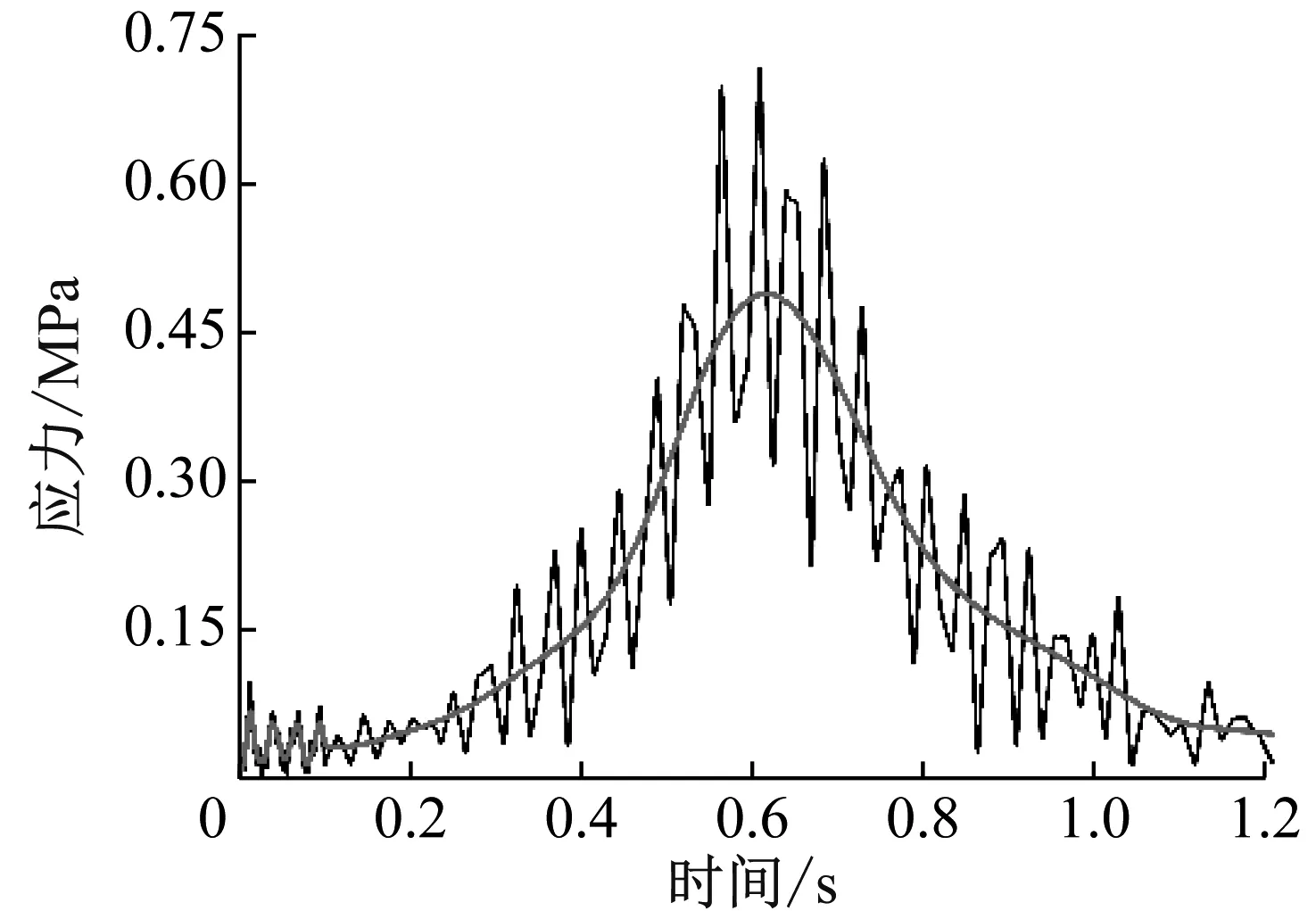
(a) 侧支撑轨枕式减振轨道应力时程曲线

由图4可知,弹性侧支撑式减振轨道道床承轨槽折角处的应力最大值为0.691 MPa;既有轨枕式减振轨道道床承轨槽底部的应力最大值为0.245 MPa。由于枕下支撑垫板材料较软,且受力面积较大,使得既有轨枕式减振轨道道床应力最大值较小。

在整体道床的最不利位置,对弹性侧支撑式减振轨道的不同部件进行应力分布的分析,得到侧支撑式弹性垫板、轨枕和整体道床的Mises应力云图如图5所示。

(a) 侧支撑式弹性垫板的应力云图

由图5可知,减振轨道的应力主要由中间承轨槽所承受,相邻的部件起到了承受部分应力的作用,整体道床的应力集中的主要部位在承轨槽的下支撑位置,部分能量向两侧承轨槽传递且吸收。整体道床的最大应力值为0.691 MPa,侧支撑式弹性垫板的最大应力为0.489 MPa,轨枕的应力集中来自扣件垂向压力,最大应力为6.27 MPa。

改变垂向载荷施加位置,将垂向载荷加载至两根轨枕的正中位置,为了保持结构的对称性,在原来的轨道上增加一根轨枕,对侧支撑式弹性垫板、轨枕和整体道床的应力分布进行分析,结果如图6所示。

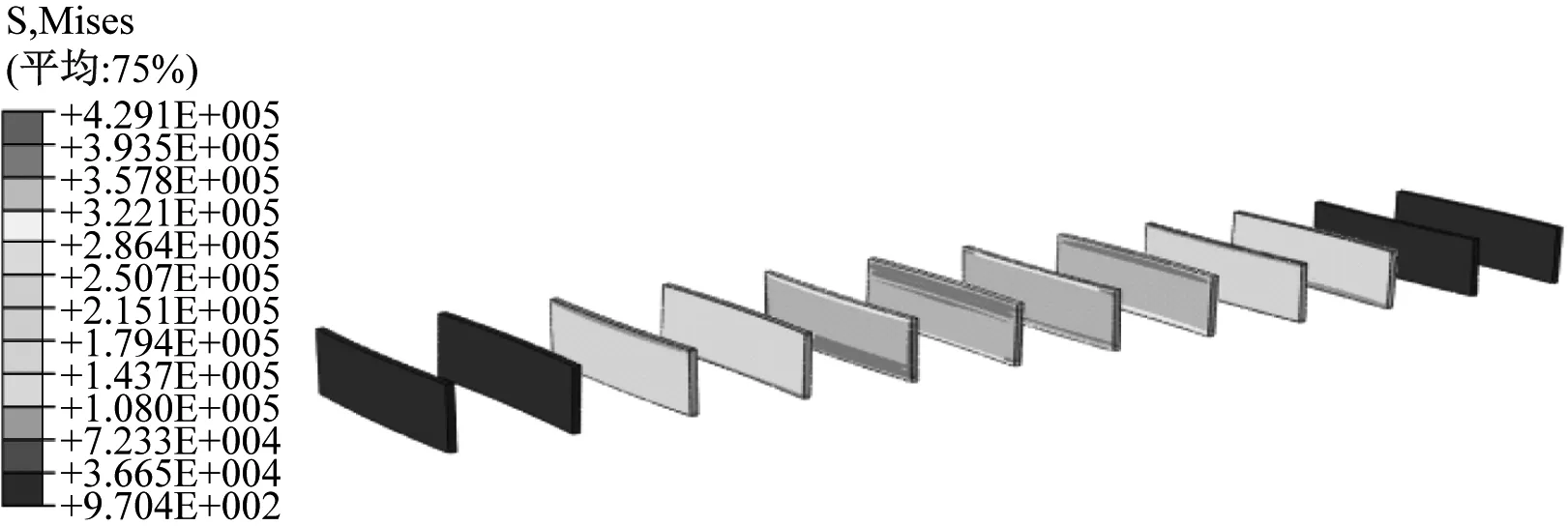
(a) 侧支撑式弹性垫板的应力云图

由图6可知,减振轨道的应力由更多的部件所承担,主要是中间两个承轨槽的部件,应力集中得到了分配,使其最大应力减小,整体道床、侧支撑式弹性垫板和轨枕的最大应力分别为0.499 MPa,0.429 MPa,5.948 MPa,相比于图5其最大应力分别减小了27.8%、12.3%和5.14%。

综上所述,对比弹性侧支撑式减振轨道在垂向载荷施加位置不同时部件的应力云图可知,垂向载荷加载至轨枕正中位置时,应力集中区域由两根轨枕共同承担,使应力值较小。

2.3 减振效果

由于两种减振轨道支撑方式不同,选取两个位置作为拾振点,并将冲击载荷(30 kN)作用于两种减振轨道中间位置,对两种道床的减振效果作对比分析。

对于侧支撑轨枕式减振轨道模型,如图7(a)所示,拾振点1选取在冲击载荷作用点正下方位置对应的道床单元处,拾振点2选取在轨枕中间位置(平行于拾振点1) 对应的道床单元处;对于下支撑轨枕式减振轨道模型,拾振点选取在与侧支撑轨枕式减振轨道模型拾振点相同位置(见图7(b))。

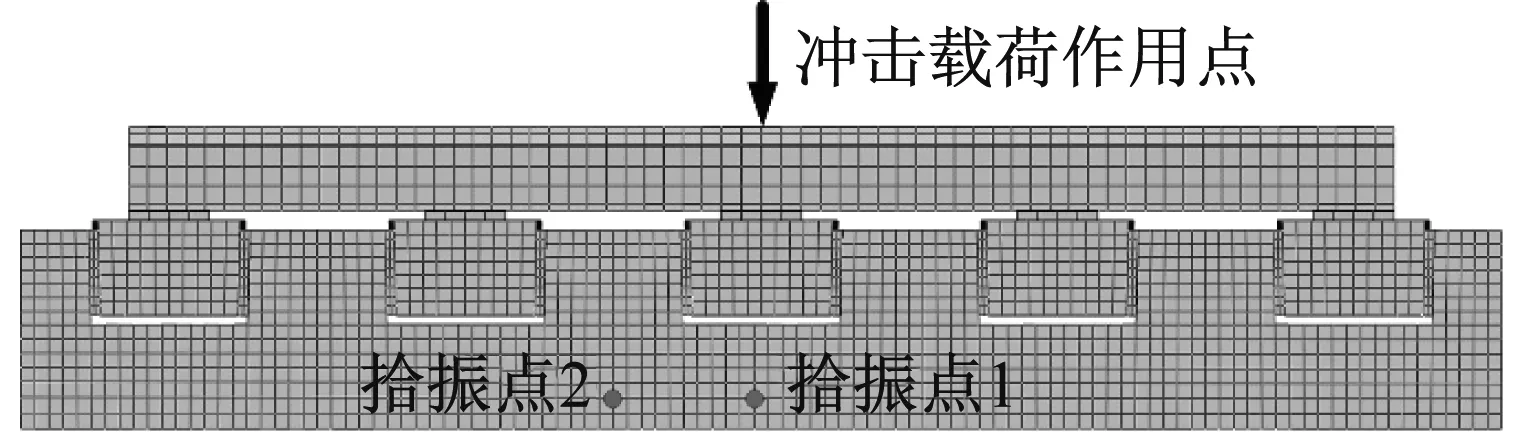
(a) 侧支撑轨枕式减振轨道

振动加速度是体现减振效果的评价指标之一。两种减振轨道道床在拾振点1与拾振点2的振动加速度曲线对比图,如图8所示。

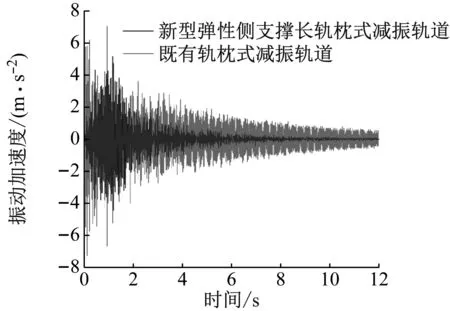
(a) 拾振点1

由图8可知,相比于既有轨枕式减振轨道,新型弹性侧支撑长轨枕式减振轨道的道床振动加速度在拾振点1整体较小,且在0.02 s之后振动幅度减小;由于向两侧传递的振动波在纵向排列的轨枕间可抵消部分能量,减少了振动能量向基础的传递,因此,拾振点2的振动加速度值相比于拾振点1较小,振动幅度减小显著,呈现较佳的减振效果。

基于振动加速度响应,进一步分析两个拾振点加速度的1/3倍频程谱。两种减振轨道道床在0～2 000 Hz范围内的1/3倍频程谱曲线对比图,如图9所示。

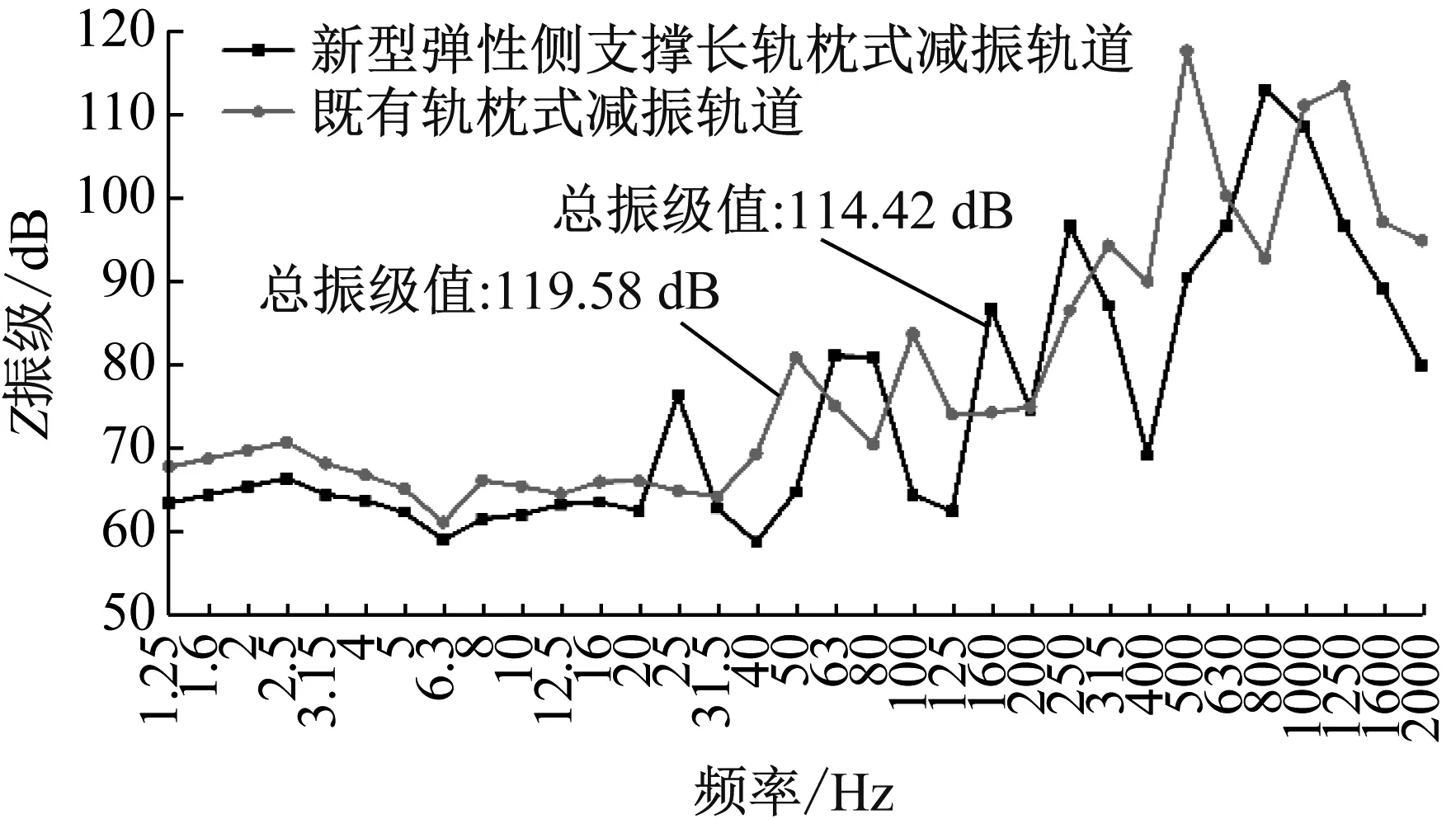
(a) 拾振点1

由图9可知,随着频率的升高,1/3倍频程谱曲线总体趋势呈现缓慢下降后上升的现象,且在低频中,振级值均较小。新型弹性侧支撑长轨枕式减振轨道的总振级值均较小,在拾振点1处减小了5.16 dB,在拾振点2处减小了7.44 dB,因此,拾振点2处减振效果更佳。

3 道床配筋检算

由2.2节分析可知,弹性侧支撑式减振轨道的整体道床的应力集中在承轨槽的折角处,既有轨枕式减振轨道的整体道床的应力集中在承轨槽的底部。在整体道床的应力分析的基础上,参考深圳地铁3号线铺装线路的配筋图,对两种减振轨道的整体道床进行配筋设计,增加抗弯性能,使之不易发生开裂,延长轨道的使用寿命。两种减振轨道的配筋截面图,如图10所示。由于道床结构相近,可以采用相同的配筋,且钢筋采用笼状的设计,增加整体结构的稳定性。

图10 道床配筋截面图Fig.10 Section diagram of the track bed reinforcement

3.1 设计载荷

由于城市轨道交通以地下线为主,本文只考虑了在隧道的配筋计算,因此,减振轨道结构设计作用仅有列车荷载。

由Q/CR 9130—2018《铁路轨道设计规范(极限状态法)》[22]可知:列车竖向荷载标准值为2倍的静轮重,横向荷载标准值为0.8倍的静轮重。列车竖向荷载的加载方式采用单轴单轮加载,加载位置在减振轨道整体道床中间轨枕的正上方。地铁A型车的轴重为160 kN,因此,列车竖向荷载标准值和横向荷载标准值分别为160 kN和64 kN。

3.2 列车荷载弯矩计算

在列车竖向荷载作用下,分别计算既有轨枕式减振轨道整体道床和弹性侧支撑式减振轨道整体道床的纵、横向弯矩[23],结果如表3所示。

表3 列车竖向荷载引起的道床弯矩Tab.3 Rail bed bending moment caused by train vertical load

3.3 配筋设计

根据荷载组合,素混凝土承载层临开裂时的边缘容许拉应力为

[σcr]=γft

(1)

(2)

式中:γ为混凝土构件的截面抵抗矩塑性影响系数;ft为混凝土抗拉强度设计值,MPa;h为承载层厚度,mm;γm为混凝土构件的截面抵抗矩塑性影响系数基本值,对于矩形截面取为1.55。

由于受到弯矩和轴力的作用,素混凝土承载层内引起的混凝土边缘拉应力为

(3)

式中:M2为列车荷载、温度梯度、基础变形等引起的承载层弯矩,kN·m;F为温度变化和收缩引起的承载层内温度拉力,MPa;b为承载层宽度,mm;h为承载层厚度,mm。

根据整体道床的结构,对钢筋笼的基本参数进行计算,钢筋笼配置参数如表4所示。

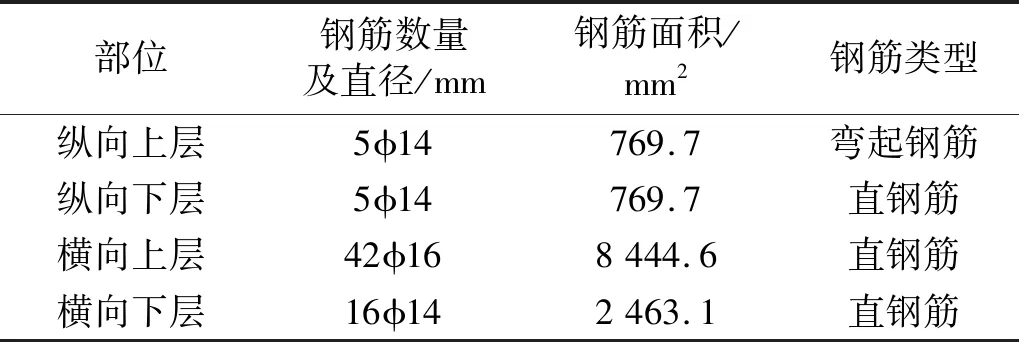
表4 钢筋笼配置参数Tab.4 Reinforcement cage configuration parameters

3.4 配筋检算

在上述载荷组合的作用下,若σ<[σcr],则表明承载层不会开裂。若σ≥[σcr],则表明混凝土承载层将出现开裂。基于承载能力极限状态的设计荷载值对减振轨道整体道床进行配筋设计。普通钢筋采用HRB400钢筋,容许应力[σs]=274 MPa,C35混凝土容许应力[σb]=15.2 MPa。减振轨道整体道床的混凝土抗拉、抗压强度设计值分别取1.57 MPa、16.7 MPa。

在载荷组合作用下,侧支撑式减振轨道整体道床纵向正弯矩最大值M纵=23.71 kN·m/m,则混凝土应力σc=M纵/W=0.65 MPa<[σcr]=2.62 MPa,钢筋应力σs=(Es/Ec)σc=4.13 MPa<[σs]=274 MPa。侧支撑式减振轨道整体道床横向正弯矩最大值M横=11.45 kN·m/m,则混凝土应力σc=M横/W=0.32 MPa<[σcr]=2.616 MPa,钢筋应力σs=(Es/Ec)σc=2.03 MPa<[σs]=274 MPa,故整体道床混凝土不会开裂。

由于整体道床的保护层厚度为35 mm,则容许裂缝宽度为0.233 mm,裂缝宽度参照TB 10002.3—2005《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》中的计算式进行计算

(4)

式中:K1为钢筋表面形状影响系数,光圆钢筋K1=1.0,带肋钢筋K1=0.8;K2为荷载特征影响系数;r1为中性轴至受拉边缘的距离与中性轴至受拉钢筋重心的距离之比,可取1.2;σs为受拉钢筋重心处的钢筋应力,MPa;ds为受拉钢筋直径,mm;ρe为受拉钢筋的配筋率。

根据配筋率和裂缝宽度的计算公式可得到计算参数,如表5所示。

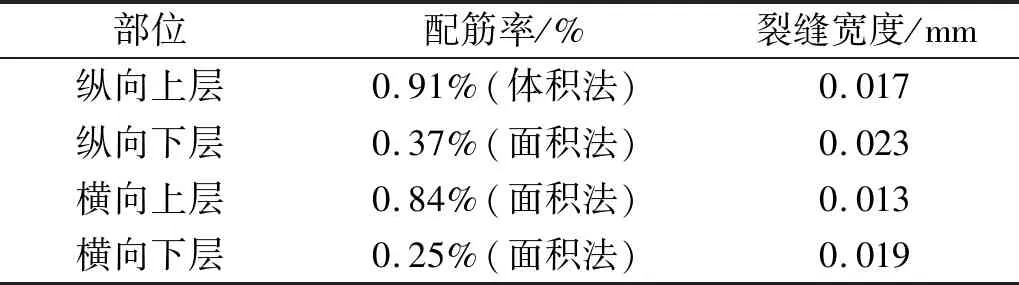
表5 道床的配筋率和裂缝宽度的计算参数Tab.5 The calculation parameters of reinforcement ratio and crack width of the track bed

由表5可知,根据构造配置钢筋,满足最小配筋率,裂缝宽度均小于容许裂缝宽度,整体道床达到强度要求。

4 动刚度特性

节点动刚度是评价轨枕式减振轨道动力学特性的重要参数。为了研究侧支撑弹性垫厚度、空间倾斜量、橡胶材料硬度对节点动刚度的影响,基于第1章所建立的有限元模型,以一个轨道单元为研究对象,首先通过理论计算和模型试验所得载荷-位移响应滞回曲线的对比,获得理论计算对侧支撑弹性垫橡胶材料特性赋值的基准,然后展开侧支撑式弹性垫板厚度、空间倾斜量、橡胶材料硬度对节点动刚度的影响研究。减振轨道单元的有限元模型及试验模型,如图11所示。

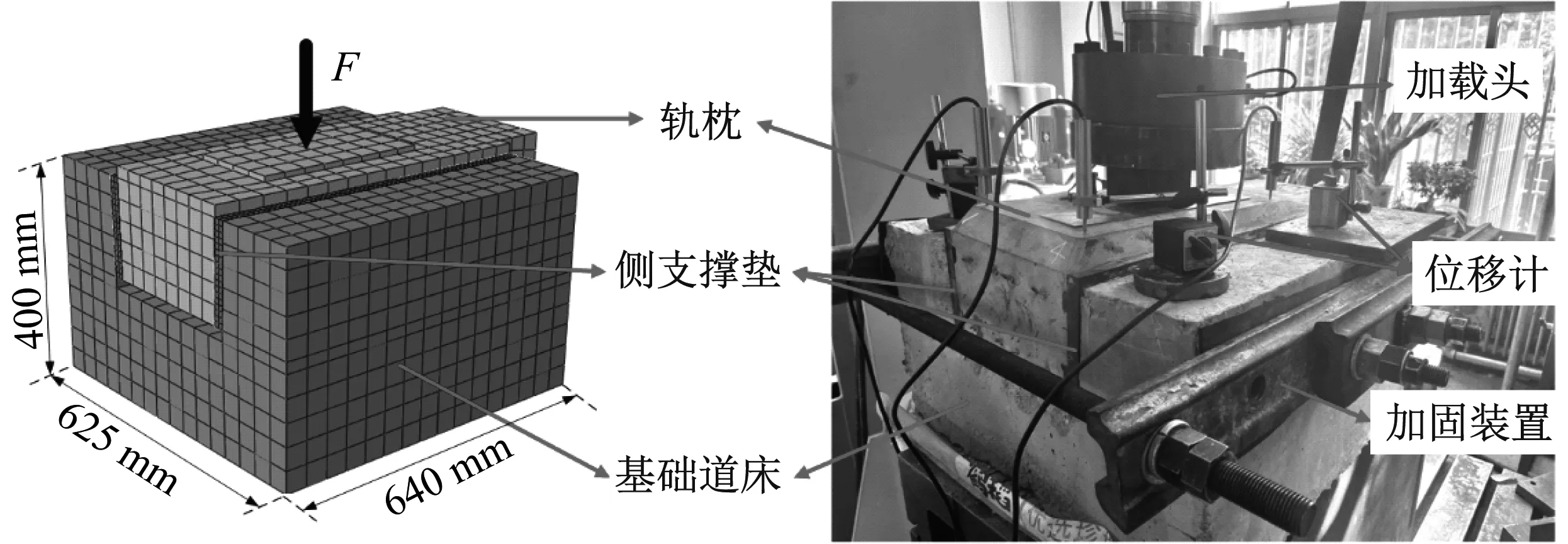
图11 减振轨道单元的有限元模型及试验模型Fig.11 Finite element model and test model of the damping track element

4.1 评价方法与试验验证

由于侧支撑式弹性垫板由橡胶材料制成,橡胶材料具有阻尼特性,故应变滞后于应力,应力的正弦波与应变的正弦波之间会形成相位差,其表现在载荷-位移曲线上就形成了一个椭圆形的迟滞曲线,如图12所示。

图12 动刚度滞回曲线Fig.12 Dynamic stiffness hysteretic curve

动刚度计算公式

(5)

式中:X1为最大位移与最小位移的差值,mm;F1为最大位移对应载荷与最小位移对应载荷之间的差值,kN;Kd为动刚度,kN/mm。

减振轨道的计算参数如下:道床整体尺寸为640 mm×625 mm×400 mm,采用C35的混凝土;轨枕则采用C50的混凝土;承轨台简化为与实际垫板大小相同的矩形体,尺寸为330 mm×170 mm×15 mm,与钢轨和轨枕用绑定的方式相连;侧支撑式弹性垫板的长度为640 mm,厚度为20 mm,空间倾斜量为5 mm,弹性模量为8.0 MPa,泊松比为0.48,并采用弹性与瑞利阻尼相结合的计算方法,其中瑞利阻尼可表示为αM+β(α为质量阻尼,β为刚度阻尼),在低频段,瑞利阻尼值可为α=0.988,β=0.007 2。

在轨枕上方施加10～40 kN的周期性正弦荷载,加载频率为5 Hz,加载时间为30 s,试验与仿真计算得到的载荷-位移响应滞回曲线的对比,如图13所示。由图13可知,理论计算结果与试验结果基本吻合,减振轨道的节点动刚度约为31.09 kN/mm。

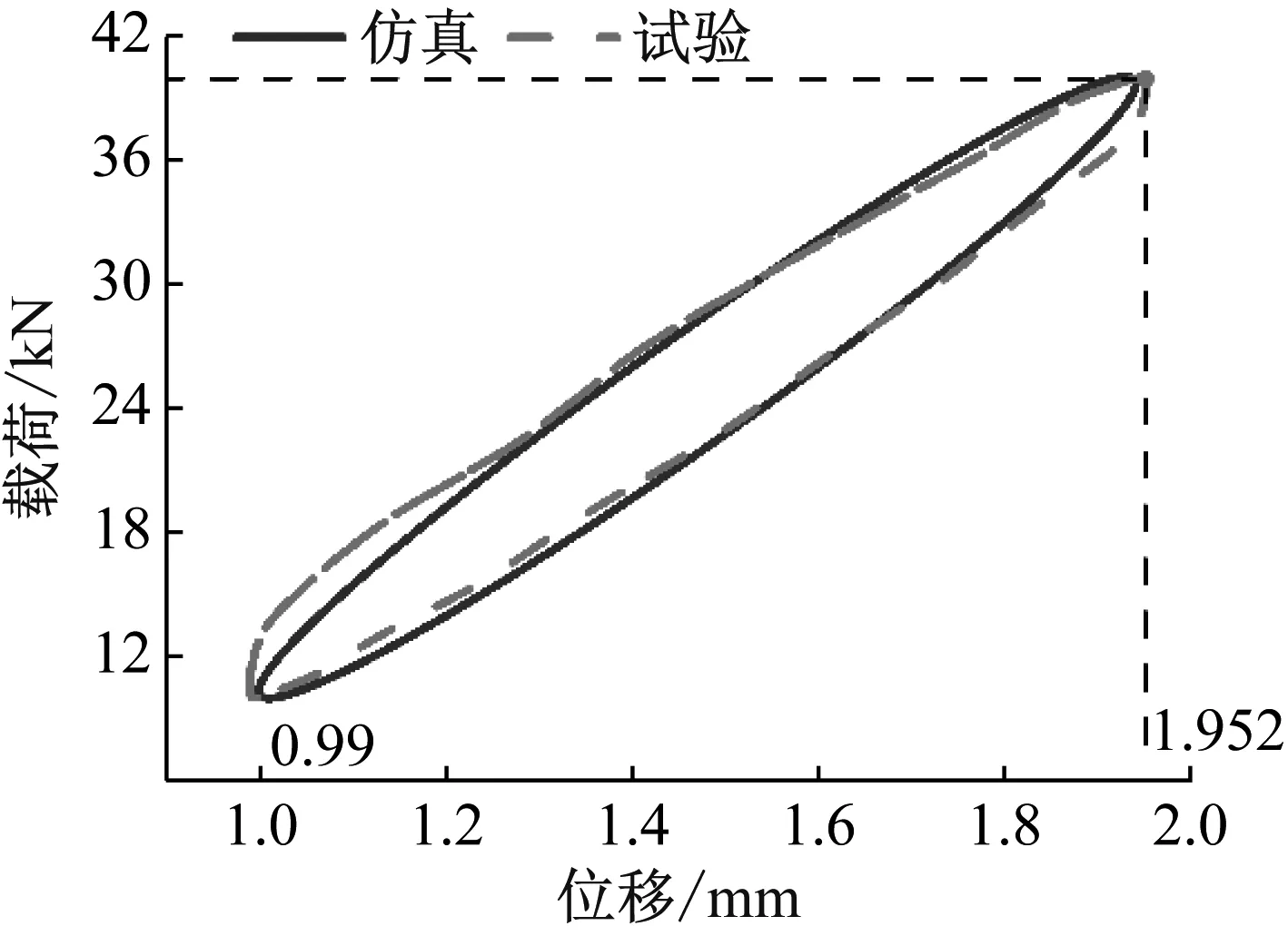
图13 载荷-位移响应滞回曲线对比Fig.13 Comparison of the hysteretic curves of load-displacement response

上述试验验证说明本文建立的新型弹性侧支撑长轨枕式减振轨道结构单元有限元模型是可以有效模拟其动刚度特性的。以厚度为20 mm,空间倾斜量为5 mm,弹性模量为8.0 MPa的侧支撑式弹性垫板为基准,分别改变上述三个关键参数,研究其变化对节点动刚度的影响规律。

4.2 厚度的影响

在加载方式和其它结构参数不变的前提下,改变侧支撑式弹性垫板的厚度,得出其对节点动刚度特性影响规律。10 mm、20 mm、30 mm和40 mm四种不同厚度的侧支撑式弹性垫板对应的载荷-位移滞回曲线对比图,如图14所示。

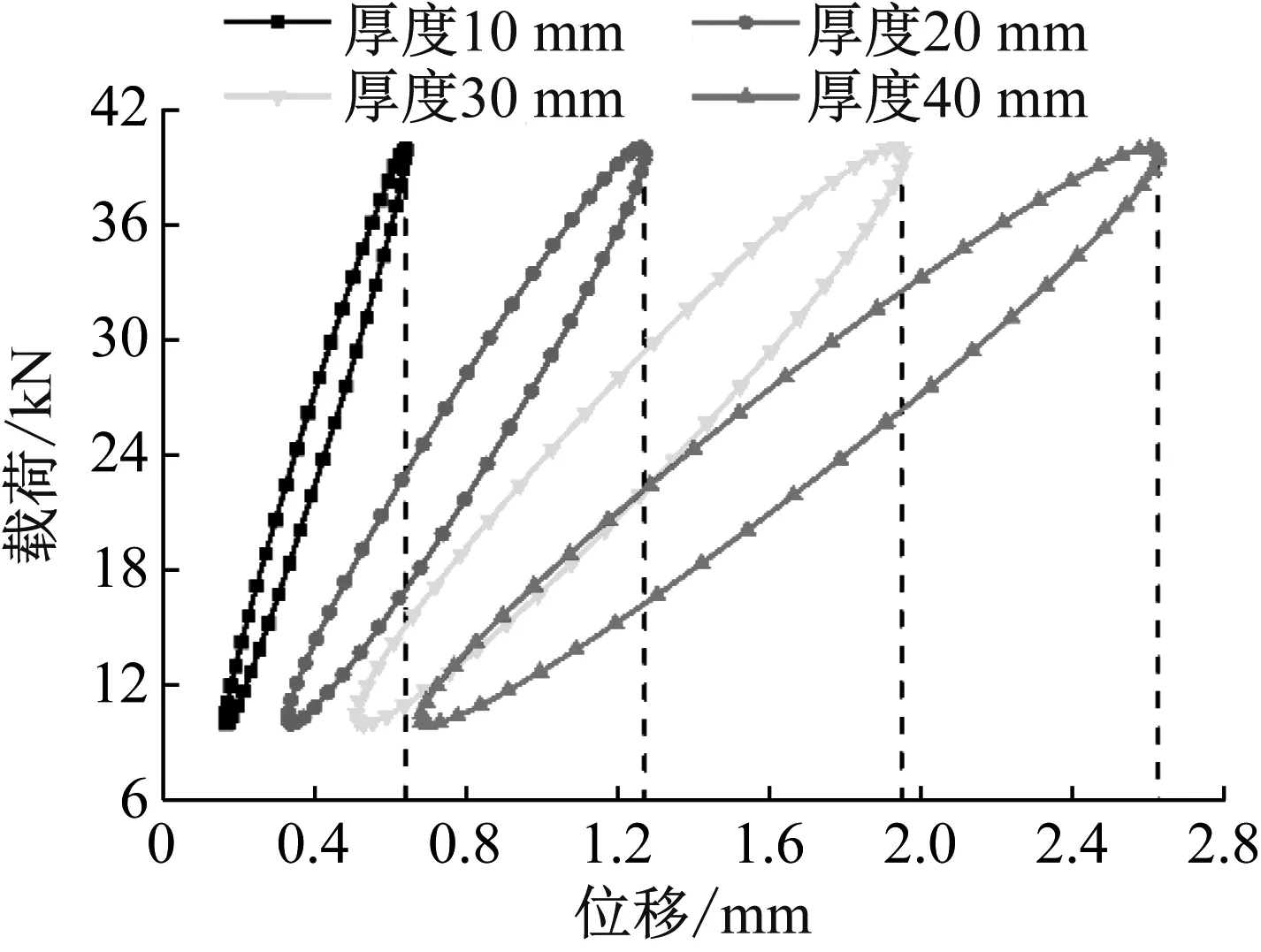
图14 厚度对载荷-位移滞回曲线的影响Fig.14 Influence of thickness on load-displacement hysteresis curve

由图14可知,随着侧支撑式弹性垫板厚度的增加,载荷-位移滞回曲线的位置向右偏移,倾斜程度减小,且曲线包络面积增大。由式(5)可知,支撑式弹性垫板厚度越大,新型弹性侧支撑长轨枕式减振轨道单元的节点动刚度越低,并且吸收、消耗振动能量的能力越强。

侧支撑式弹性垫板厚度对节点动刚度和垂向最大位移的影响规律曲线,如图15所示。

图15 厚度对结构单元力学性能的影响Fig.15 Influence of thickness on mechanical properties of structural elements

由图15可知,垂向最大位移随侧支撑式弹性垫板厚度的增加呈线性增长趋势。节点动刚度随侧支撑式弹性垫板厚度的增加呈指数规律递减,当厚度小于20 mm时,节点动刚度受侧支撑式弹性垫板厚度的影响更加显著。

4.3 空间倾斜量的影响

保证其它结构参数和加载方式不变,改变侧支撑式弹性垫板的空间倾斜量,得出其对节点动刚度特性影响规律。2 mm、5 mm、12 mm和24 mm四种不同空间倾斜量的侧支撑式弹性垫板对应的载荷-位移滞回曲线对比图,如图16所示。

由图16可知,随着侧支撑式弹性垫板空间倾斜量的增大,载荷-位移滞回曲线的位置向左偏移幅度较小,倾斜程度增大,且曲线包络面积减小,当空间倾斜量小于12 mm时,载荷-位移滞回曲线几乎重叠。与图14相比,曲线包络面积随空间倾斜量的变化较小。

侧支撑式弹性垫板空间倾斜量对节点动刚度和垂向最大位移的影响规律曲线,如图17所示。由图17可知,空间倾斜量对轨枕的垂向最大位移和节点动刚度影响显著,随着侧支撑式弹性垫板空间倾斜量的增大,垂向最大位移呈指数规律递增,而节点动刚度近似呈线性递减趋势变化。

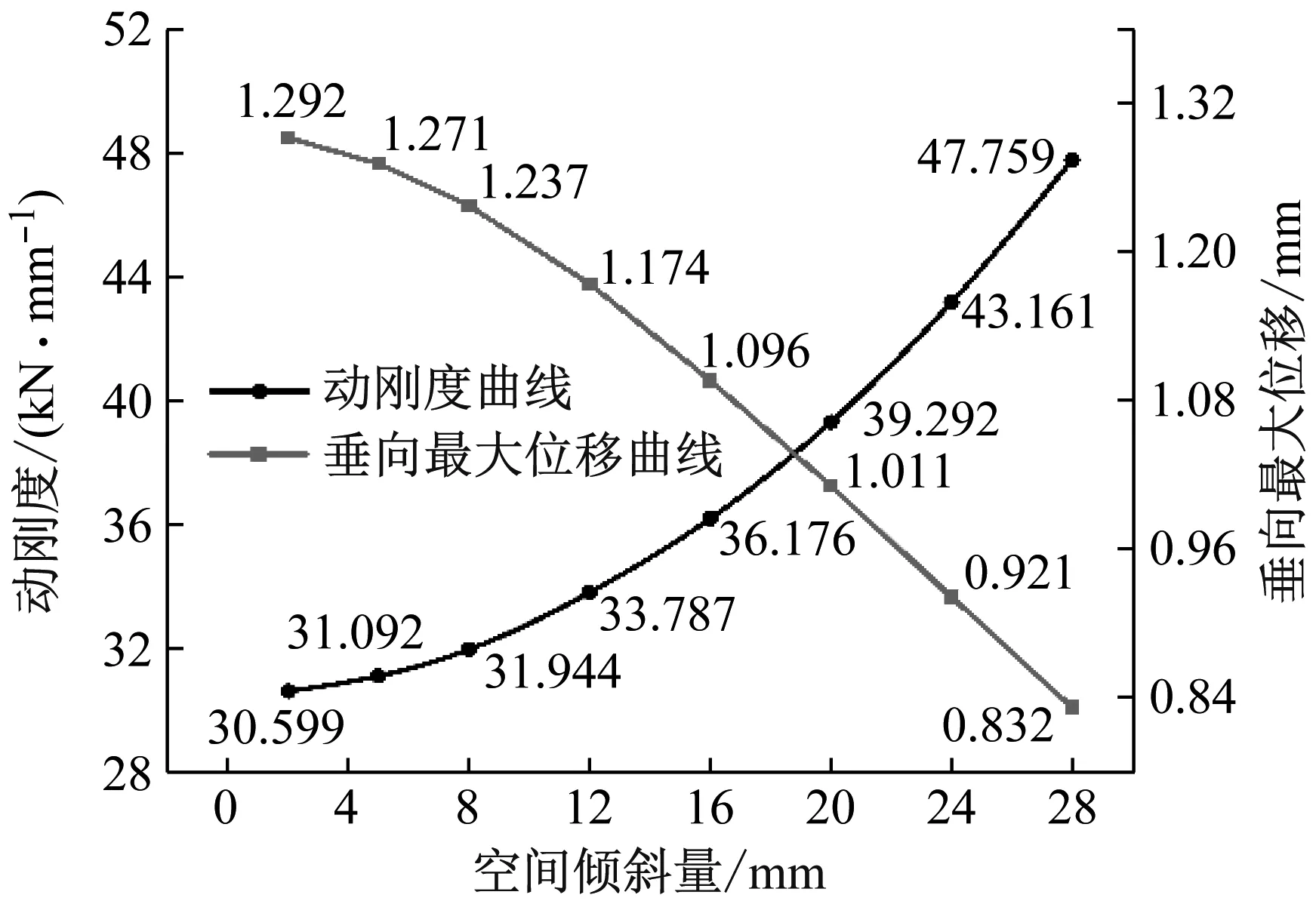
图17 空间倾斜量对结构单元力学性能的影响Fig.17 Influence of spatial inclination on mechanical properties of structural elements

4.4 材料硬度的影响

与前两节相同的前提下,改变材料硬度,得出其对节点动刚度特性影响规律。侧支撑式弹性垫板按五种不同硬度的材料考虑时,轨枕对应的载荷-位移滞回曲线对比图,如图18所示。

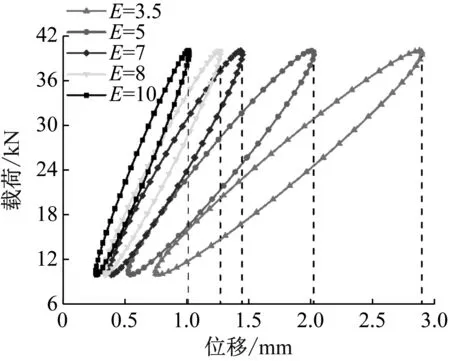
图18 材料硬度对载荷-位移滞回曲线的影响Fig.18 Influence of material hardness on load-displacement hysteresis curve

由图18可知,随着侧支撑式弹性垫板材料硬度的增大,载荷-位移滞回曲线的位置向左偏移,倾斜程度增大,曲线包络面积减小显著,且材料硬度和厚度对载荷-位移滞回曲线的影响变化规律相同。由式(5)可知,侧支撑式弹性垫板材料硬度越大,新型弹性侧支撑长轨枕式减振轨道单元的节点动刚度越大。

侧支撑式弹性垫板材料硬度对节点动刚度和垂向最大位移的影响规律曲线,如图19所示。

由图19可知,垂向最大位移随侧支撑式弹性垫板材料参数的增大呈指数规律递减。节点动刚度随侧支撑式弹性垫板材料参数的增大呈线性增长趋势。

通过上述三个关键参数对节点动刚度和轨枕位移的的影响规律分析可以看出侧垫厚度和材料硬度变化对节点动刚度和轨枕位移的影响较侧垫空间倾斜量的影响更为显著。增加侧垫厚度,降低材料硬度会增大侧垫的剪切变形量,导致节点刚度降低;并且使载荷-位移滞回曲线的面积增大,可以消耗更多的振动能量。

根据既有规范,轨枕式减振轨道节点最大位移量不能超过4 mm,从图15、图17和图19可以看出,厚度、空间倾斜量和材料硬度三个关键参数在本文所研究的取值范围内是满足规范要求的,在上述参数范围内可以通过适当取值,获得不同减振等级要求的侧支撑式弹性垫板设计参数。

5 结 论

本文以新型弹性侧支撑长枕式减振轨道为研究对象,建立了有限元模型,分析得出道床最不利位置及应力集中区域,评价道床的减振效果,并进行了配筋设计与检算;试制了1:1结构单元模型,通过理论计算与实测数据对比,确定了关键参数研究基准;研究了侧支撑式弹性垫板的厚度、空间倾斜量和材料硬度三个关键参数对减振轨道节点位移和动刚度的影响规律。主要结论如下:

(1) 在轮载作用下与传统的相比,轨枕两侧的道床区域参与支撑,应力增大,应力集中区域在承轨槽两侧下端的折角处。当载荷施加在轨枕正上方时应力最大,为0.691 MPa。减振效果较佳。

(2) 对弹性侧支撑长枕式减振轨道道床进行配筋设计和检算,得到配筋率和裂缝宽度均在要求范围之内,钢筋应力和混凝土应力均小于许用应力,承轨槽两侧下端折角处不会开裂。

(3) 侧支撑式弹性垫板的厚度和材料硬度对节点动刚度的影响较大,空间倾斜量对节点动刚度的影响较小。增加侧垫厚度,降低材料硬度可以有效降低新型弹性侧支撑长轨枕式减振轨道的节点刚度,提高侧垫的变形耗能效果。

(4) 三个关键参数取值范围对垂向最大位移变化范围满足既有规范的要求,通过三个关键参数不同的取值组合,可获得不同减振等级要求的侧支撑式弹性垫板设计参数。