光伏并网的宽频振荡问题分析

苏乐，程静，2，王维庆，2

（1.新疆大学 电气工程学院，新疆 乌鲁木齐 830047；2.可再生能源发电与并网技术教育部工程研究中心，新疆 乌鲁木齐 830047）

随着能源危机的加重，越来越多的新能源加入到电力系统当中，光伏发电在新能源当中占比较大，光伏并网引入了些许的电力电子元件且控制较为复杂，系统参数众多，容易发生相互作用而引发电力系统数Hz 到数百Hz 的振荡[1-3]。故光伏并网对电力系统的稳定性影响需要进行多方面的考虑与分析，找到引发系统各频段振荡的根源，从而采取一定的措施，提高系统的稳定性。文献[4]采用特征值分析法研究了大规模光伏电站的振荡模式，然而作者的分析不太全面，仅仅对系统中的次同步振荡和低频振荡进行了分析，对于更高频率的振荡并未给出详细的分析；文献[5]利用特征值和参与因子分析了影响系统振荡的主要因素，然而作者在建模时并未将串联补偿线路考虑在内，故而分析有失全面性；文献[6]建立了含串联补偿线路的新能源并网系统的小信号模型，并借鉴复转矩系数法，分析了不同串补度情况下串联补偿线路对电流控制与直流电压控制的影响，然而作者在建模时并未考虑光伏电池、最大功率点跟踪（maximum power point tracking，MPPT）控制及直流转直流（DC-DC）变换器、锁相环等环节，故而对系统的分析也不全面；文献[7]建立了考虑控制延时环节的光伏并网逆变器的状态空间小信号模型，利用特征值分析方法研究了宽范围电网强度下考虑控制延时的光伏并网逆变器稳定性问题，其建模仍是以逆变器及后边的滤波电路、串补电路为主，并未考虑逆变器之前的光伏电池、MPPT控制及DC-DC变换器的影响；文献[8]建立了光伏并网系统状态空间模型，通过系统状态空间矩阵，运用根轨迹分析法研究了控制参数对系统振荡模态的影响，优化参数选取范围，并仿真验证了其正确性，然而在数学建模过程当中亦未考虑逆变器前边的升压及最大功率寻踪环节。

本文为研究光伏并网对电力系统振荡的影响，综合考虑了光伏电池、MPPT 控制及DC-DC变换器、逆变器、锁相环、滤波器以及串联补偿线路在内的多个因素，对系统进行了全面建模；然后研究了系统各个振荡模态与光伏系统之间的关系，分析了光伏并网系统发生振荡的可能性与振荡机理；并根据分析结果对系统参数进行优化；最后通过Simulink仿真验证了分析的正确性。

1 模态分析法

模态分析法又叫小干扰稳定分析法，也叫特征值分析法，该方法不仅可以让我们知道电力系统是否稳定，还可以让我们了解到系统的振荡起因以及具体的影响因素[9]。

要进行小干扰稳定性分析，首先要建立系统的线性化微分方程：

其中

式中：x为电力系统中的各个状态变量；f(x)为状态变量间的函数关系。

将微分方程在平衡点x0处进行泰勒展开，略去高阶无穷小量可得到：

根据李雅普诺夫第一定理，非线性系统的小干扰稳定性是由该系统线性化后特征方程的根，即雅可比矩阵A的特征值决定。

当状态矩阵A的所有特征值均位于复平面的左侧时，其对应的是一种衰减的振荡模态，在遭受小扰动一段时间后，系统会重新回到初始平衡点运行；当A的特征值出现正实根或具有正实部的复根时，说明此系统在初始平衡点是不稳定的，前者对应的是非周期性失稳，后者对应于周期性失稳；当矩阵A存在零实部的特征值时，说明系统的初始平衡点处在临界情况。

若雅可比矩阵的特征值为λ=δ±jω，则该特征值对应的振荡频率为

阻尼比为

阻尼比可以反映振荡模态的衰减速度，阻尼比ζ的值越大，振荡幅值随时间衰减的速度就越快。

为了确定状态变量和各模态之间的关系，将系统状态矩阵A的左右特征向量结合起来形成了参与矩阵P，如下式：

参与矩阵P的元素Pki=ukivki称为参与因子，它描述了第k个状态变量Δxk对第i个模态的参与程度，P的第i列Pi为第i个模态的参与向量。

2 光伏发电系统建模

本文所建立的光伏并网系统的结构如图1所示。光伏并网系统可分为光伏阵列、MPPT 控制部分、Boost 升压电路、逆变器及其控制部分、LCL滤波器、锁相环、串联补偿电路、交流电网等。

图1 光伏并网系统示意图Fig.1 Diagram of photovoltaic grid-connected system

2.1 光伏电池建模

本文的光伏电池模型是通过标准工况下（S=1 000 W/m2，Tref=25 ℃）的4个电气参数（短路电流isc、开路电压uoc、最大电流im、最大电压um）来推导非标准状况下的u—i特性方程：

式中：upv，ipv分别为光伏阵列的输出电压和输出电流。

将式（6）线性化可得到：

2.2 光伏发电系统的MPPT控制及DC-DC变换器模型

光伏发电最大功率寻踪是通过控制光伏电池的输出口电压upv，使光伏电池的输出在外界环境发生改变时始终保持在最大功率点附近，控制框图如图2所示。

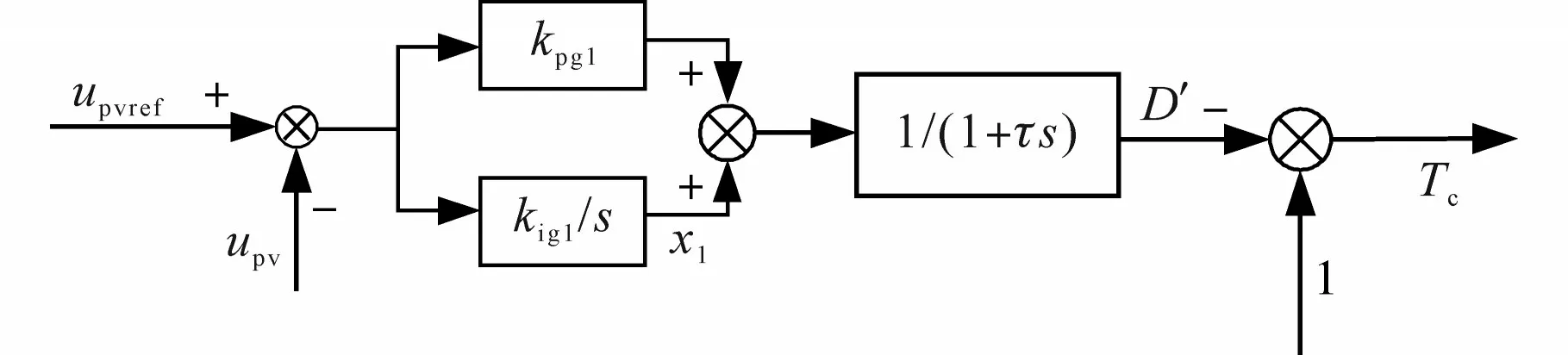
图2 光伏发电最大功率寻踪控制框图Fig.2 Photovoltaic power generation maximum power tracing control block diagram

本文的MPPT 采用的是电导增量法，由于光伏阵列输出功率为

求导可得：

当dP/dupv＞0 时，upv小于最大功率点电压upvref；当dP/dupv＜0 时，upv大于最大功率点电压upvref；当dP/dupv= 0，upv等于最大功率点电压upvref。

将上述3 种情况代入式（11）可得：当upv＜upvref时，dipv/dupv＞-ipv/upv；当upv＞upvref时，dipv/dupv＜-ipv/upv；当upv=upvref时，dipv/dupv=-ipv/upv。这样可以根据dipv/dupv与-ipv/upv之间的关系来调整工作点电压，从而实现最大功率跟踪。

图2 中，upv为光伏阵列的输出电压；upvref为MPPT输出的电压参考值；kig1，kpg1为MPPT控制环节的比例积分控制参数；τ为时间常数；x1是为了方便描述MPPT 控制电路的数学模型而引入的状态变量；Tc为占空比。

由图2 可得到MPPT 控制部分的线性化数学模型：

图3 是DC-DC 变换器控制框图。图中，LB为滤波电感，iB为流过滤波电感的电流，idc为流入逆变器的电流，Cpv为滤波电容，Cdc为直流母线电容，udc为逆变器输入电压。

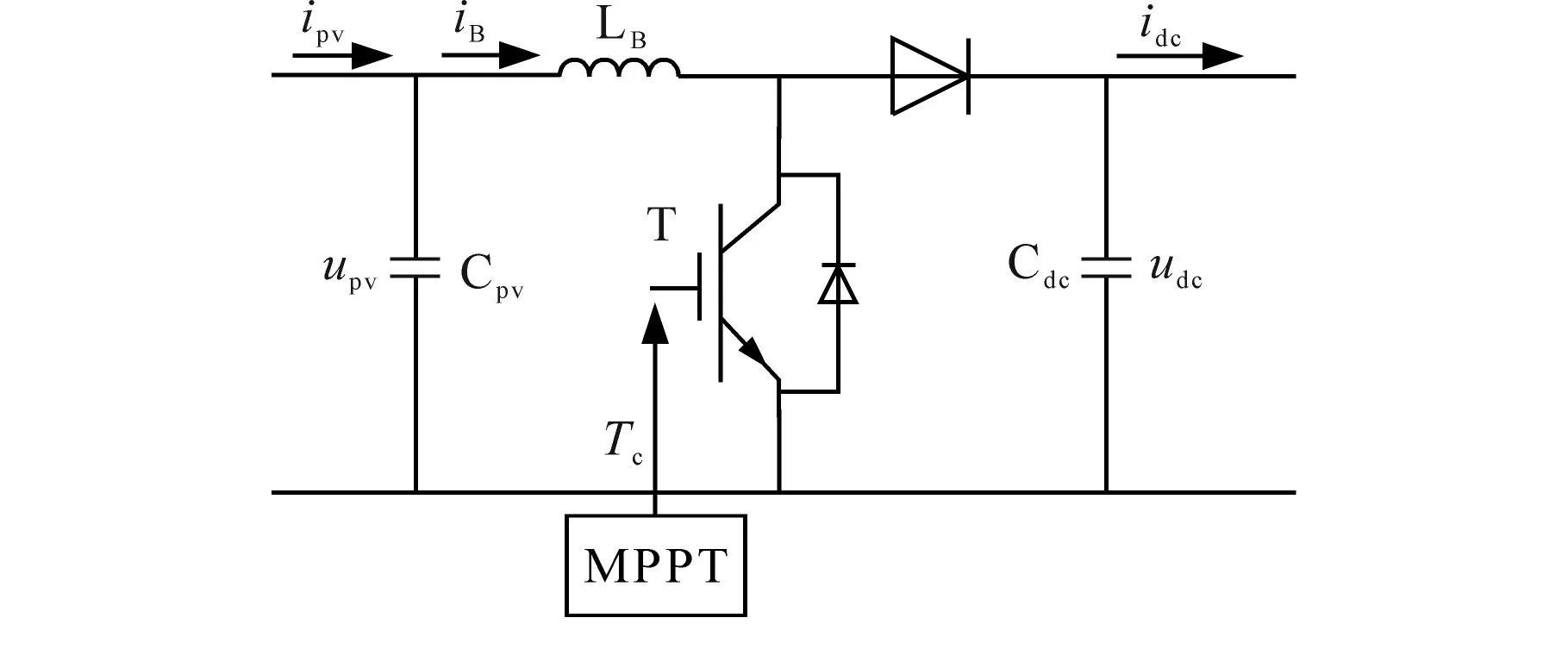
图3 DC-DC变换器控制框图Fig.3 DC-DC converter control block diagram

根据图3建立数学模型并线性化可得到：

2.3 光伏逆变器控制模型

光伏逆变器的控制系统由d-q坐标系下的直流电压外环、d轴电流内环、q轴电流内环组成。其控制框图如图4所示[10-11]。

图4 光伏逆变器控制框图Fig.4 PV inverter control block diagram

图4中，udc为直流电容的端电压；udcref为直流电容端电压的参考值；kpg2，kig2分别为光伏逆变器直流电压控制外环的比例和积分系数；kpg3，kig3分别为d轴电流内环的比例和积分系数；kpg4，kig4分别为q轴电流内环的比例和积分系数；uccd，uccq分别为光伏发电系统经过LCL 滤波器输出的d，q轴电压的实际值；uLdref，uLqref分别为光伏逆变器输出d，q轴控制电压；ω0为电网参考角频率；LL为滤波器电感。为了更好地描述光伏逆变器控制系统的数学模型，引入中间状态变量x2，x3，x4。

由图4可得到如下方程：

2.4 光伏发电系统的锁相环建模

光伏逆变器采用电流矢量控制，需要在d-q坐标系下对电流的d，q轴分量分别进行控制，因此需要加入锁相环来实时跟踪光伏系统输出端口的电压相位，从而方便根据相位进行坐标变换，实现系统的电流矢量控制[12]。光伏系统的锁相环控制框图如图5所示。

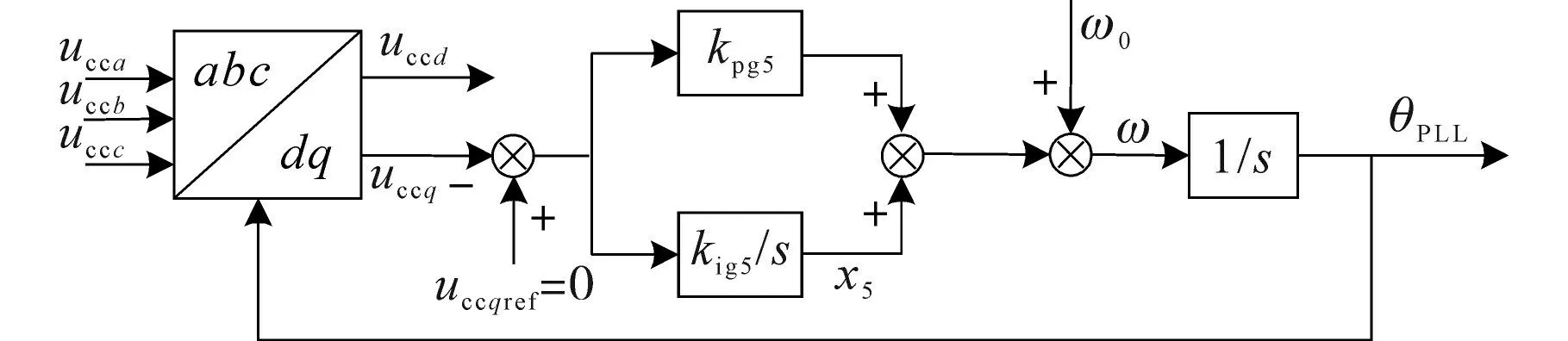
图5 锁相环控制框图Fig.5 Phase-locked loop control block diagram

图5 中，uccabc为逆变器的输出经过滤波器与变压器之后的电压；uccd，uccq为转换到d-q坐标系下的d，q轴电压分量；uccqref为q轴电流的参考值；kpg5，kig5为锁相环控制环节的比例、积分系数；θPLL为锁相环得到的电网角度；x5为引入的中间变量。根据图5可得到光伏逆变器锁相环的线性化状态方程：

2.5 光伏发电系统的滤波器及串补线路的模型

为了方便计算，将图1 进行进一步归算与简化，得到了光伏系统的滤波器与串补的简化模型，如图6所示。

图6 滤波器及串补模型Fig.6 Filter and serial complement model

图6中，uL，iL为逆变器的输出电压、电流；CL，LL为LCL 滤波器的滤波电容以及逆变器侧的滤波电感；uc为滤波电容的端电压；RC，CC，LG为串联补偿电路的电阻、电容以及归算后的电感；uCc为串联补偿电容的端电压；uG为电网电压。在图1 中，L1，L2分别为LCL 滤波器的逆变器侧电感和串补侧的电感，LC为串补电感。将L2归算至串补中，此时图6 中的LL等于图1 中的L1，LG=L2+LC。根据图6以及LC 元件的特性，可以列出滤波器及串补电路的线性化状态方程：

联立可得到光伏系统的全阶数学模型：

其中

式中：ΔXg为光伏系统的状态变量；Ag为光伏系统的状态矩阵。

3 光伏发电系统的振荡模态及参与因子分析

光伏发电系统的主要参数如表1所示。通过Matlab 编程计算，可以得到给定参数下的系统的特征值分布情况如图7所示。

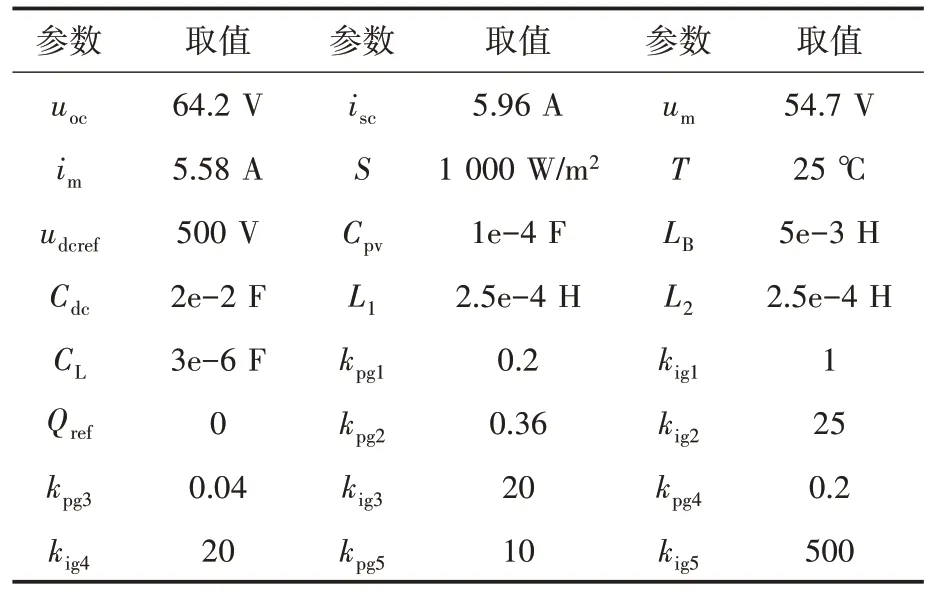
表1 光伏发电系统的主要参数Tab.1 The main parameters of the photovoltaic power generation system

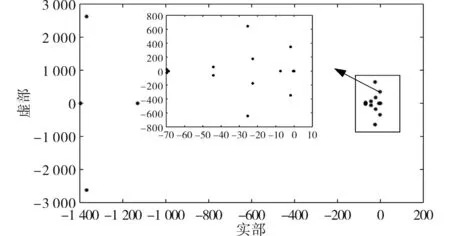
图7 光伏发电系统的特征值分布图Fig.7 Characteristic value distribution of photovoltaic power generation system

当特征值出现共轭复根时表示系统会出现振荡，共轭复根实部为正时系统会发生持续振荡，实部为负时系统振荡逐渐收敛，所以本文重点分析图7 中6 组具有共轭复根的特征值，其具体参数如表2所示。

表2 系统状态矩阵的主要特征值Tab.2 The primary eigenvalue of the system state matrix

为了得到每个振荡模态的具体影响因素，对表2 中的6 对特征值进行了深入的分析，分别计算了每个特征值的参与因子，并进行了归一化整理，得到了图8。

图8 光伏发电系统的振荡模态与参与因子Fig.8 Oscillation mode and participation factor of photovoltaic power generation system

由图8 可知，串补对振荡模态λ1,2，λ5,6，λ7,8，λ11,12均有一定的影响，线路中串补电容的等效电抗值XC占原线路等效电抗XL（包括变压器与线路电抗）的百分比为线路串补度，串补度可由k=XC/XL表示。将串补度由0.55 依次降到0.35 可以得到系统的特征值分布，如图9 所示。从图9中可以观察到，随着串补度的降低，系统的振荡频率均有所下降，稳定性有所提高。

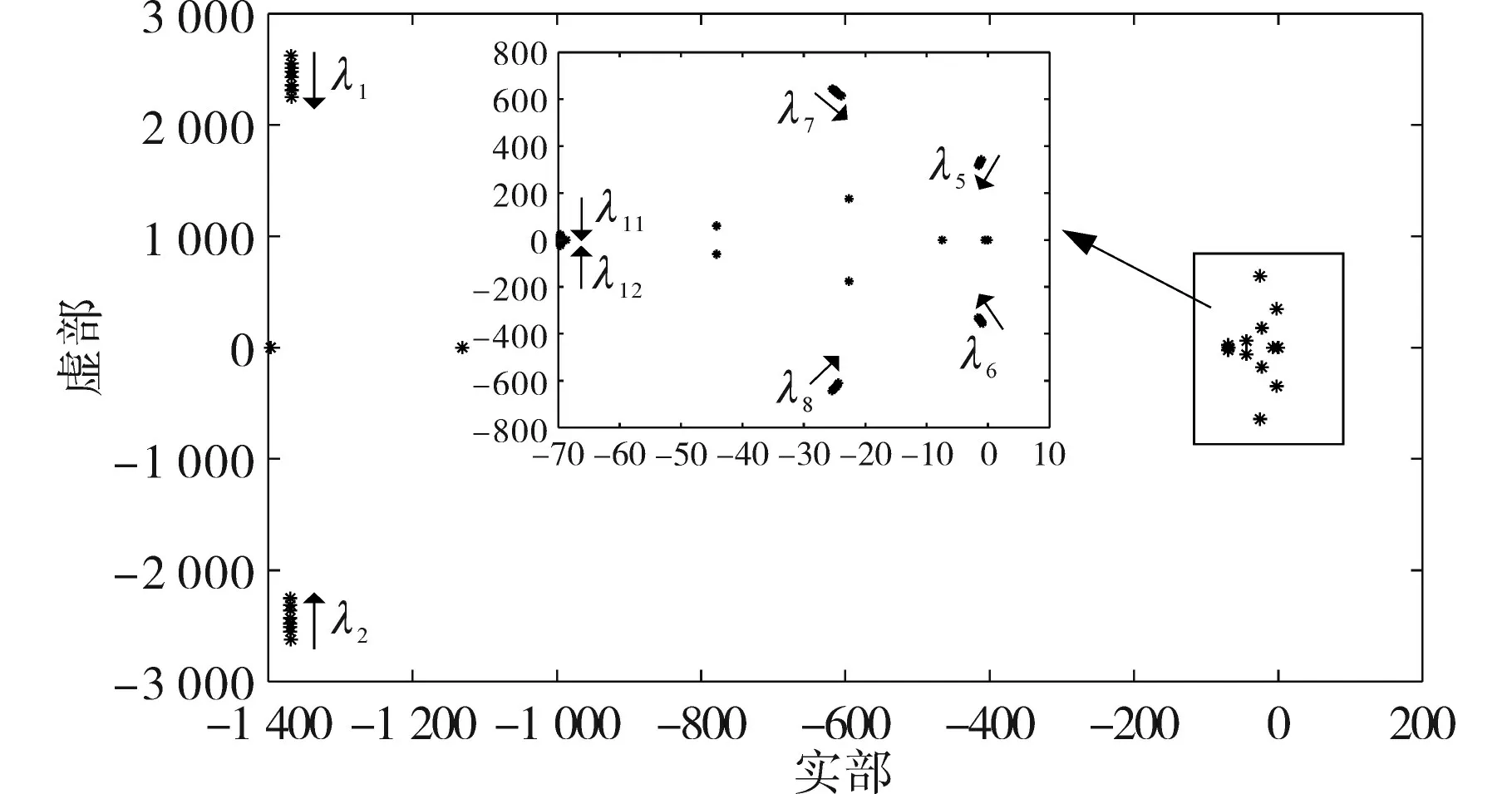
图9 串补度降低对系统振荡模态的影响Fig.9 The influence of reduced string complement on the oscillation mode of the system

滤波器对振荡模态λ1,2，λ5,6，λ7,8，λ11,12也有一定的影响，滤波器对振荡的影响主要与靠近逆变器的桥臂电感L1有关，当L1由2.5e-4 逐渐增大至2.5e-3时，系统的特征值变化如图10所示。从图10 可知，随着滤波器桥臂电感L1的增加，光伏发电系统的特征值均会向左偏移，这说明适当地增大滤波电感有益于系统的稳定。

图10 LCL滤波器的滤波电感增加对系统振荡模态的影响Fig.10 The influence of increasing the filtering inductance LCL filter the system oscillation mode

振荡模态λ1,2还与电压外环控制相关，使其控制参数在0.2～5 倍的初始值范围内依次增加，步长为0.1，可得到该特征值的变化情况如图11所示。

图11 电压外环控制参数变化对振荡模态λ1,2的影响Fig.11 The influence of voltage outer loop control parameter changes on the oscillation mode λ1,2

振荡模态λ3,4与MPPT的PI控制以及光伏阵列的输出相关，设置PI 控制参数为给定值的0.2～5倍，取步长0.01，得到图12所示的特征值变化曲线。

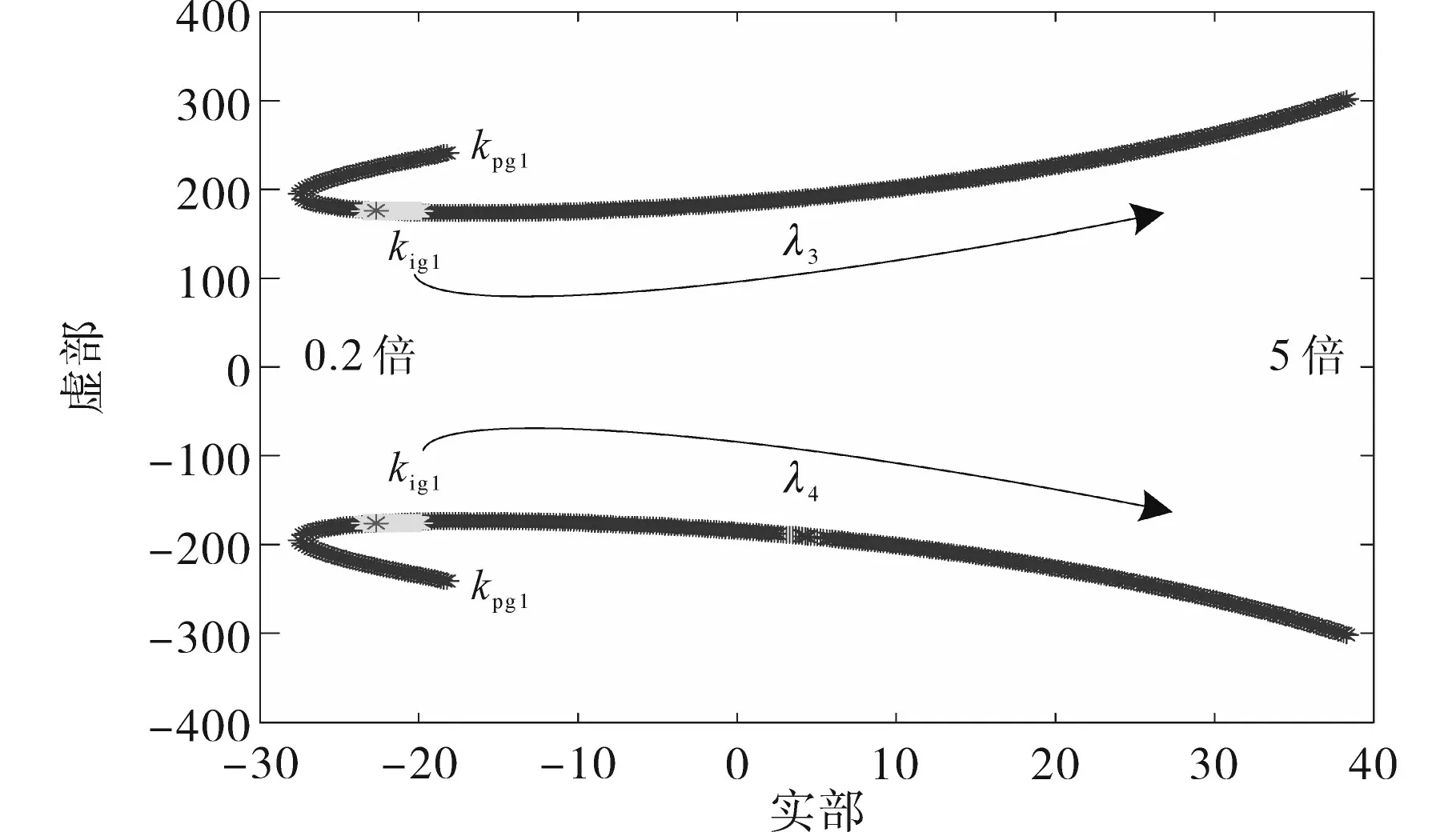
图12 MPPT控制参数变化对振荡模态λ3,4的影响Fig.12 The influence of MPPT controls parameter changes on the oscillation mode λ3,4

光伏阵列的输出受到其串并联光伏电池的数目影响，振荡模态λ3,4与光伏阵列的输出有关，即与光伏电池的串并联数目相关，分别计算了串联数目在5～15 之间、并联数目在60～100 之间该振荡模态所对应的特征值，并将该特征值的变化曲线绘制于图13和图14当中。

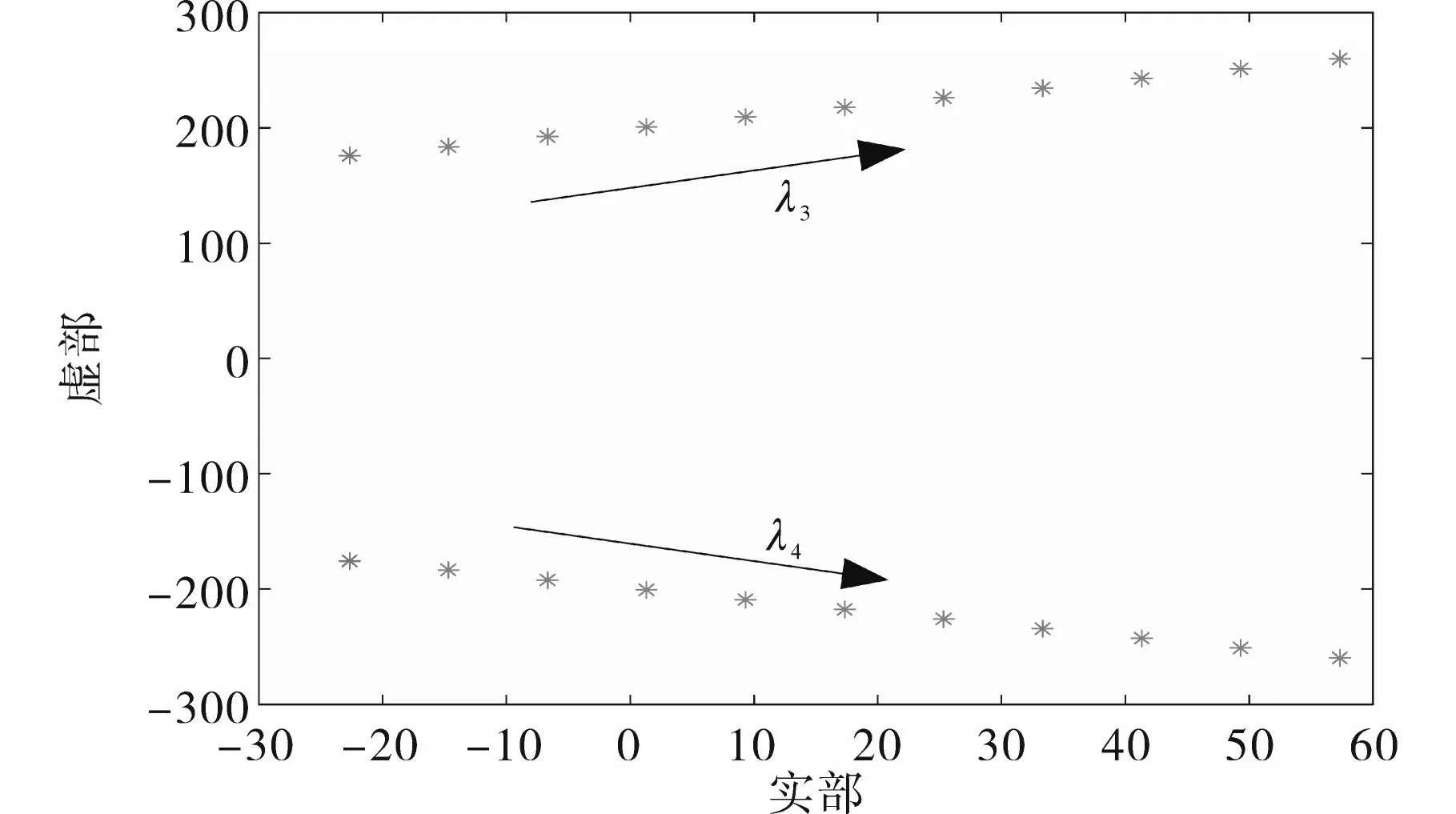
图13 光伏阵列的串联电池数目对振荡模态λ3,4的影响Fig.13 The influence of the number of series cells in a photovoltaic array on the oscillation mode λ3,4

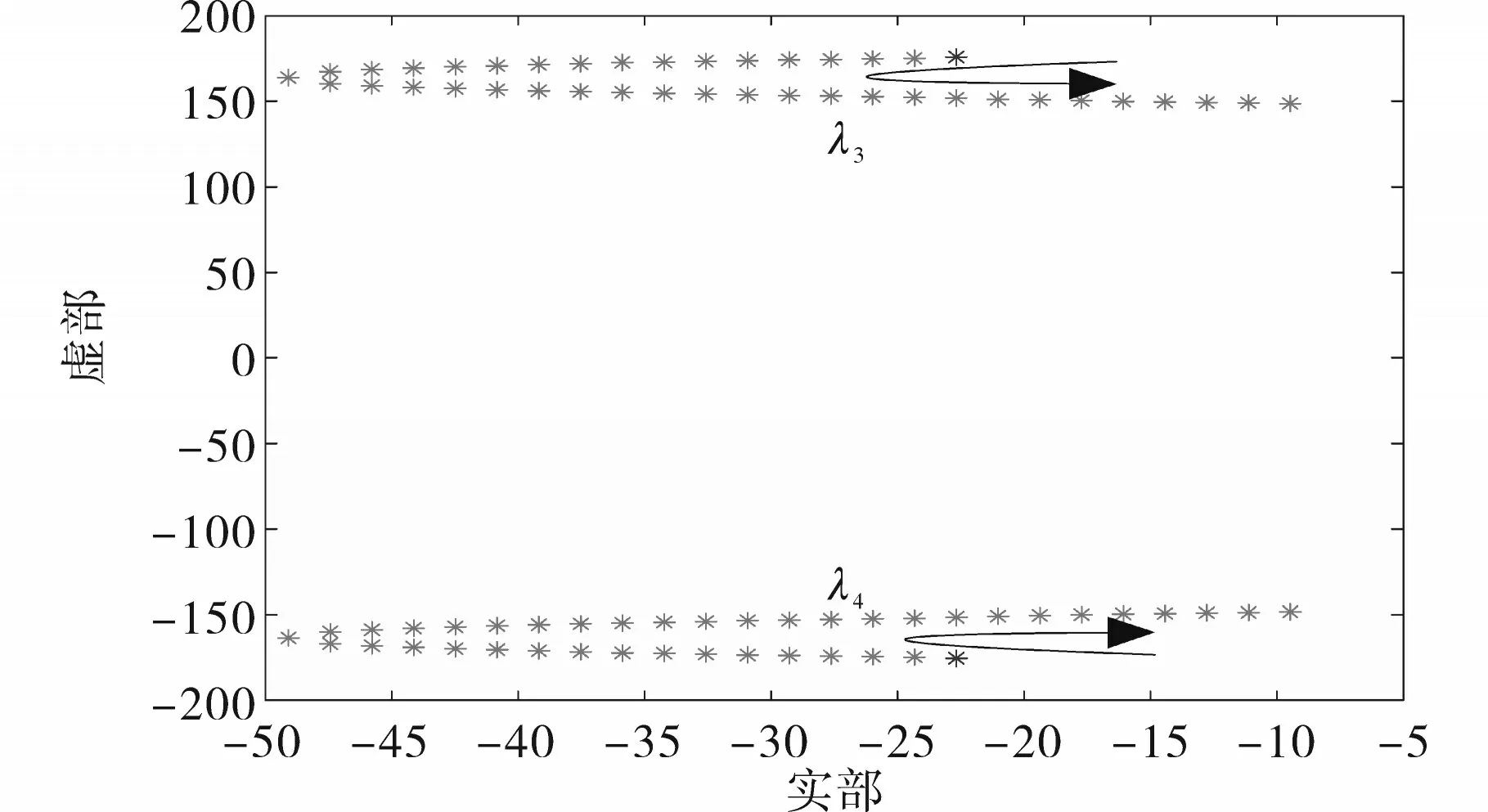
图14 光伏阵列的并联电池数目对振荡模态λ3,4的影响Fig.14 The influence of the number of parallel cells in a photovoltaic array on the oscillation mode λ3,4

振荡模态λ5,6除了受到LCL 滤波器的影响，还受到逆变器的q轴电流内环控制的影响，设置其PI 控制参数为给定值的0.2～5 倍，取步长为0.01，得到如图15所示的特征值变化曲线。

图15 q轴电流内环控制对振荡模态λ5,6的影响Fig.15 The influence of the q-axis current inner loop control on the oscillation mode λ5,6

振荡模态λ7,8除了受到LCL 滤波器的影响，还受到逆变器的d轴电流内环控制和q轴电流内环控制的影响，设置d，q轴内流内环控制的PI 参数为给定值的0.2～5倍，取步长为0.01，得到如图16所示的特征值变化曲线。

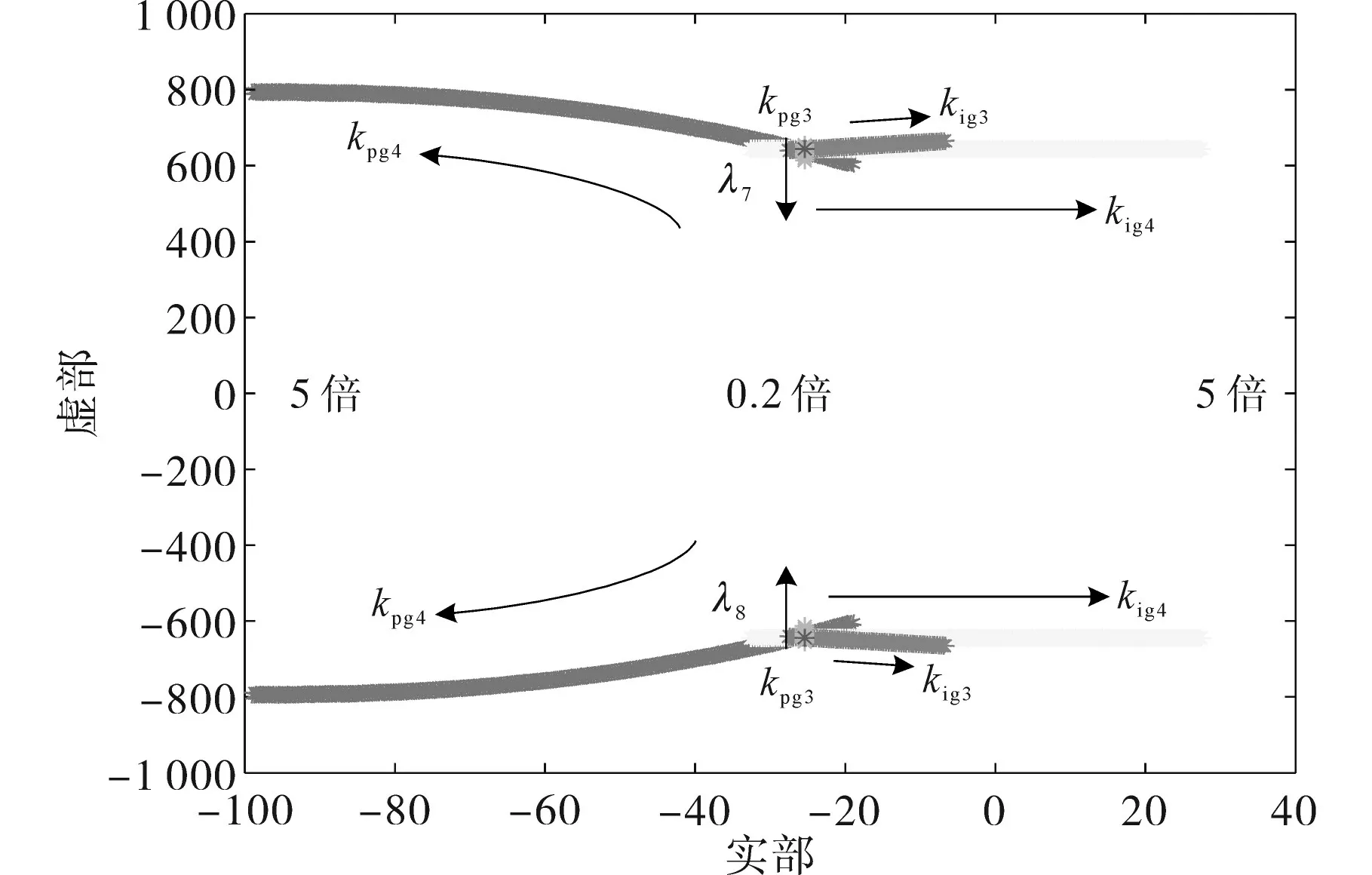
图16 逆变器电流控制对振荡模态λ7,8的影响Fig.16 The influence of inverter current control on the oscillation mode λ7,8

振荡模态λ9,10主要与锁相环相关，设置锁相环PI 控制参数为给定值的0.2～5 倍，取步长为0.01，得到如图17所示的特征值变化曲线。

图17 锁相环控制参数对振荡模态λ9,10的影响Fig.17 The influence of phase-locked loop control parameters on the oscillation mode λ9,10

振荡模态λ11,12除了受滤波器和串补的影响，也与光伏逆变器的控制环节密切相关，设置逆变器的PI控制参数为给定值的0.2～5 倍，取步长为0.01，得到如图18所示的特征值变化曲线。

图18 逆变器控制参数对振荡模态λ11,12的影响Fig.18 The influence of inverter control parameters on oscillation mode λ11,12

观察图9～图18 可知，系统的特征值随着参数的变化在不断进行变化，由前文可知系统的稳定性与阻尼比关系密切，故而对图9～图18 中的阻尼比进行计算，得到各个振荡模态的阻尼比与系统中主要参数的关系如表3所示。

表3 各个振荡模态的阻尼比与系统中主要参数的关系Tab.3 The relationship between the damping ratio of each oscillation mode and the main parameters in the system

表3 中，↗表示上升，↘表示下降，↗↘表示先上升再下降。从表中可以得到以下结论：增加并联电池数、减少串联电池数、降低串补度、增加滤波电感参数均可增大系统的阻尼比，提升系统的稳定性；kpg1和kig1与振荡模态λ3,4关系密切，kpg1增大时λ3,4的阻尼比先增大后降低，减小时λ3,4的阻尼比下降，kig1减小时λ3,4的阻尼比增大，增大时λ3,4的阻尼比减小，说明减小kig1和适当增大kpg1有利于提升系统的稳定性；kpg2和kig2与振荡模态λ1,2和λ11,12关系密切，kpg2增大或kig2减小时，λ1,2和λ11,12的阻尼比均增大，kpg2减小时，λ1,2的阻尼比增大、λ11,12的阻尼比减小，kig2增大时，λ1,2的阻尼比减小、λ11,12的阻尼比增大，说明适当的增大kpg2以及减小kig2可以增强系统的稳定性；kpg3和kig3与振荡模态λ7,8和λ11,12关系密切，kpg3增大时，λ7,8的阻尼比增大、λ11,12的阻尼比减小，kpg3减小时，λ7,8的阻尼比减小、λ11,12的阻尼比增大，从表1 可知λ7,8的阻尼比远小于λ11,12，所以在调整kpg3时应适当地增大，以提高λ7,8的阻尼比来增强系统整体的稳定性，kig3增大后，λ7,8和λ11,12的阻尼比均降低，减小后增大，说明适当增大kig3有利于系统的稳定；kpg4和kig4与振荡模态λ5,6，λ7,8和λ11,12关系密切，当kpg4增大时，λ5,6的阻尼比先增大后降低、λ7,8和λ11,12的阻尼比均增大，当kpg4减小时，这3 个振荡模态的阻尼比均下降，当kig4增大时，这3 个振荡模态的阻尼比均下降，kig4减小时，阻尼比均增加，这说明适当地增加kpg4、减小kig4有利于系统的稳定；kpg5和kig5与振荡模态λ9,10关系密切，当kpg5增大时，λ9,10的阻尼比增加，减小时，λ9,10的阻尼比减小，当kig5增大时，λ9,10的阻尼比下降，减小时，λ9,10的阻尼比增加，说明适当地增加kpg5、减小kig5可以起到增强系统稳定性的作用。

根据表3 及上述分析对系统参数进行调整，取得的优化后的参数如表4所示。

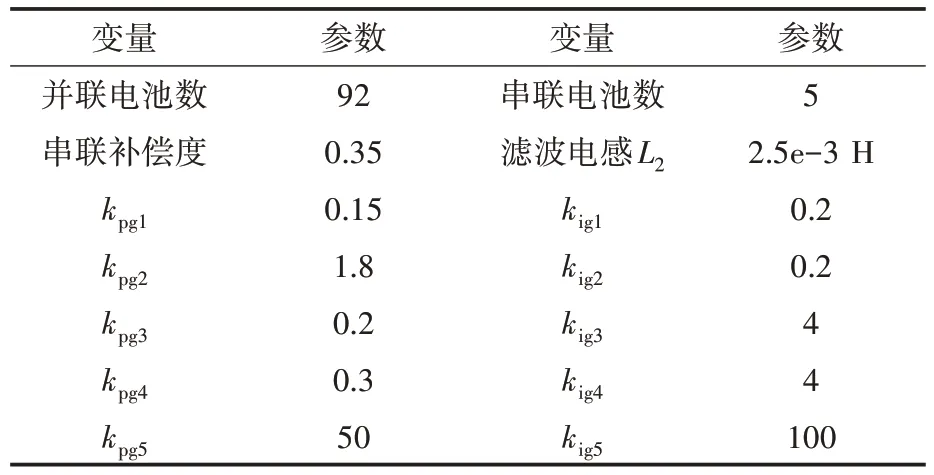
表4 优化后的系统参数Tab.4 Optimized system parameters

在仿真软件Matlab 中搭建了光伏发电系统的仿真模型，光伏阵列工作在光照强度为1 kW/m2、温度为25 ℃的条件下，经过直流升压、逆变、滤波、交流升压、远距离输送后并入25 kV 的电力系统，光伏发电系统由100台0.1 MW 的发电单元经过100 个逆变器并入电网，等值为1 台10 MW 的发电阵列经过一台逆变器接入电力系统。参数优化后的系统特征值如表5所示。

表5 优化后的系统特征值Tab.5 Optimized system characteristic values

对比表2和表5可知，系统各个振荡模态的阻尼比在经过参数的优化之后都得到了一定的提升，振荡频率除λ3,4，λ7,8，λ11,12有略微的增大外，其余振荡频率均是减小的。

为验证参数优化的结果，对系统进行了仿真，在0.4 s 时系统的MPPT 开始工作，0.5 s 时达到了稳定状态。分别对系统优化前、后的输出电压进行了快速傅里叶变换，得到了图19 所示的频谱图。

图19 光伏系统参数优化前后输出电压的频谱对比图Fig.19 Spectrum comparison diagram of output voltage before and after optimization of photovoltaic system parameters

在系统1 s 时设置了三相短路故障，故障持续时间为0.02 s，得到了如图20 所示的发生三相短路故障时系统有功功率输出的变化曲线。

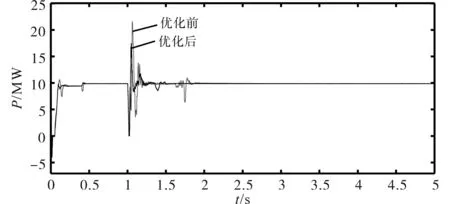
图20 光伏系统参数优化前后功率输出对比图Fig.20 Comparison chart of power output before and after optimization of photovoltaic system parameters

从图19 可知，系统参数优化前、后的振荡频率与前文的分析结果基本一致；从图20可以看出，光伏发电系统的参数经过分析及优化处理后，输出功率在系统发生短路故障时，输出功率的最大振幅由21.69 MW 下降至17.06 MW，振荡的收敛时间由1.95 s缩短至1.53 s，说明系统的稳定性有所提高。验证了前文中数学建模及分析的正确性，提高了新能源并网的电力系统的稳定性。

4 结论

本文针对光伏并网的新能源系统建立了包含光伏电池、MPPT 控制及Boost 升压电路、逆变器控制系统、滤波器、锁相环、串联补偿电路在内的详细的线性化数学模型，并对系统进行了深入的分析，研究了系统各个参数对振荡的影响，并分析了各个参数与具体振荡之间的关系，然后通过参数优化，提高了系统的稳定性，并在Simulink当中进行了仿真验证，证明了数学建模及参数优化的正确性。