基于两阶段鲁棒优化的电力系统运行灵活性容量评估模型

唐君毅，董雪涛，秦艳辉

（1.国网新疆电力有限公司电力科学研究院，新疆 乌鲁木齐 830001；2.新疆电力系统全过程仿真重点实验室，新疆 乌鲁木齐 830001）

可再生能源发电可以减少温室气体排放，推动可持续发展，受到了重点关注。美国有37个州实施了可再生能源投资组合标准，要求电力公司促使可再生能源发电量占比达到10%～33%[1]。中国的双碳目标，更是需要大规模可再生能源的参与才能得以实现[2]。以可再生能源为主体的新型电力系统将在运行上面临全新的挑战，可调度发电机组频繁启停次数、爬坡速率和备用容量要求同传统电力系统区别较大[3]。基于此，电力系统灵活性的概念被广泛关注。

在可再生能源迅速发展、能源结构低碳化转型的背景下，电力系统正由确定性系统向强随机性系统转变[4]。目前针对不确定因素的建模主要有两种方法：随机优化方法和鲁棒优化方法[5]。随机优化方法以确定性的概率分布描述可再生能源出力的特性，其经济性较好[5]。文献[6]综合考虑风光出力不确定性、波动性及相关性特征，基于随机优化方法，构建系统灵活性需求量化模型，给出了满足给定置信度下灵活性要求的发电调度方案。文献[7]考虑了在低碳目标下的风能和太阳能发电在时间和空间耦合相关性，基于构建的随机模型，提出了时空灵活性管理的方法，有效解决可再生能源发电和负荷的时间趋势和空间相关性研究。文献[8]认为灵活性有助于适应风力发电等可再生能源不断增长带来的不确定性，提出了风力不确定性下电力系统灵活性增强连续时间随机调度的数学模型和新的变换方法。文献[9]考虑发电系统和用电负荷存在不确定性的情况下，构建了一个两阶段的随机优化模型，并考虑逻辑变量、整数变量、混合变量和概率变量等因素，提出了随机模型预测控制技术和混合整数二次规划方法对模型进行了求解。文献[10]考虑了不同的灵活性来源，并在实时调度时考虑了它们各自的响应时间，提出了一种基于加权情景的两阶段随机规划模型来优化多时段最优潮流日前调度，有效地激活可用的灵活性服务。上述文献采用的随机优化方法普遍存在求解难度大、场景复杂的问题，难以进行广泛应用。鲁棒优化方法是通过鲁棒集的形式对不确定因素建模，相较于随机优化方法，在求解上具有简便性，并且可以同时满足所有的约束。文献[11]提出了一种风电场综合电力系统的两阶段自适应鲁棒协调发电与输电扩容规划模型，利用多面体不确定集刻画了需求、风力的不确定性，将所提出的难处理模型重新构造为一个可处理的混合整数线性规划问题，并利用仿射策略进行求解。文献[12]基于两阶段鲁棒算法，提出了一种综合考虑异构可再生能源设备、网络运行约束和不平衡潮流模型的系统级多周期电力灵活性的新方法。文献[13]将实时经济调度问题描述为一个多阶段的鲁棒模型，将多阶段鲁棒规划分解为动态规划形式，提出了快速鲁棒对偶动态规划算法。文献[14]提出了一种基于自适应鲁棒优化的含可再生能源和非可再生能源及电动汽车停车场等灵活性电源的有源配电网的双目标优化调度模型，利用鲁棒方法对不确定参数进行建模。

目前针对电力系统灵活性方面的研究大多基于日前运行调度展开，未深入考虑再调度、弃风和切负荷成本的影响。首先，文章提出了一种基于两阶段鲁棒优化方法的电力系统运行灵活性评估数学模型，该模型可以定量评估电网的运行灵活性容量。第一阶段，假设可再生能源出力是确定的，以运行成本、弃风、切负荷最小化为目标函数；第二阶段，考虑可再生能源出力的不确定，对第一阶段的运行调度策略进行调整。然后针对不确定因素，构建一类可调的鲁棒集进行刻画。最后，采用CCG 算法对模型进行求解，通过在改进的IEEE RTS 24 节点测试系统运行数据以验证评估方法的有效性。

1 基于可调鲁棒区间的调度模型

将不确定性集作为一个决策变量，在最小化系统运行成本的同时实现最优不确定性集。在此模型下找到整个系统在安全稳定运行的情况下可以接受的最大不确定区域。模型中，考虑运行成本最小化会导致不确定性集合变窄，而考虑弃风和切负荷成本会增大风力发电的不确定性集合。因此，目标函数由最小化运行成本、弃风成本和切负荷成本三部分组成，如下式所示：

式中；F为目标函数；i为常规机组集合；k为风电机组集合；t为评估周期；cpi为机组运行成本系数；为机组i在评估周期t内的出力；cui，cdi分别为常规机组i的启、停成本系数；ubit，vbit分别为常规机组i在评估周期t内的启、停状态；，分别为弃风、切负荷成本系数；，分别为风电机组k的预测出力区间的上、下界；，分别为实际可接入风电机组k出力区间上、下界。

通过式（1）评估最优不确定性灵活性容量区间，如果风力超过系统上限，则进行弃风，相反则进行切负荷。

可调鲁棒区间调度模型的约束条件如下：

1）机组发电的最小启/停时间约束为

2）机组的启动和关闭状态约束为

式中：为时间段t时常规机组的是否启动或停机的二元变量。

3）常规火电机组的容量约束为

式中：Pmini，Pmaxi分别为常规火电机组出力上、下界。

4）火电机组的爬坡约束为

式中：RUi，RDi分别为机组上、下爬坡速率。

5）线路传输容量约束为

式中：l为传输线路集合；Hil，Hkl，Hml为传输因子；Fmaxl为传输线路最大输电能力；m为系统负荷集合；dmt为负荷需求。

6）系统功率平衡约束为

7）风电场的出力限制如下式：

式中：ωkt，分别为风电实际出力和预测出力。

在第一阶段中，确定决策变量ωUB和ωLB，约束（式（12）和式（13））为这两个变量的边界约束。

不确定因素表征在第二阶段完成，分别如下所示：

8）机组发电能力约束为

9）机组的爬坡能力约束为

10）输电线路潮流约束为

在两阶段模型中可以看出，由于可调不确定性集合减小而导致的第一阶段调度计划中的弃风、切负荷，使得所有不确定性都能满足功率平衡和输电线路限制约束。

2 改进的调度模型

可调鲁棒区间的调度模型基于可调不确定性集合，利用不确定性集边界作为可再生能源出力的调度信号。对于特征不确定性集合之外的不确定性因素，可能会发生第二阶段优化中，造成额外的弃风或切负荷成本。本文在此模型基础上，提出一种新的两阶段模型。第一阶段，对机组出力进行了优化调整；第二阶段中，考虑再调度、弃风、切负荷的成本最小化。因此，构建了以下可调鲁棒模型：

式中：cri为备用成本系数；为考虑风电不确定性下的机组备用。

式（18）为目标函数，Frobust表示风电场先进行生产调整所对应的系统最小化运行成本，进而在考虑不确定因素下最坏再调度最小化成本，相较于式（1），改进的调度模型中强调了对不确定因素的鲁棒性约束。各约束条件分别如下：

1）线路潮流约束：

2）功率平衡约束：

3）不确定性之间为线性关系约束：

改进的调度模型在原可调鲁棒区间调度模型的基础上，将约束条件式（10）～式（13）调整风电场的调度发电容量外，进一步调整了系统的不确定性区间；约束条件式（21）和式（22）假设风力发电对系统施加的不确定性之间为线性关系；在约束条件式（23）中，qkt的变化范围在0～1 之间，其改进后的调度模型的算法流程图如图1所示。

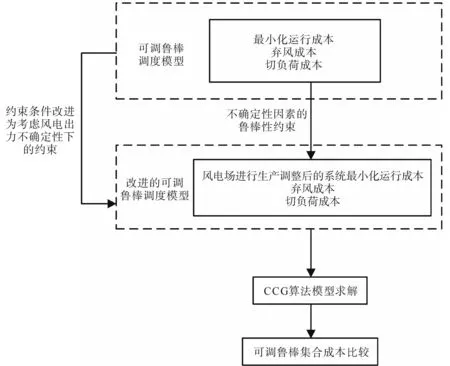
图1 改进后可调鲁棒区间模型算法流程图Fig.1 Flow chart of improved adjustable robust interval model algorithm

3 模型求解

求解此两阶段鲁棒模型的关键在于第二阶段中约束（式（14）～式（17））的数量巨大，在求解之前，需要对模型进一步转化，使其成为符合CCG 算法求解的形式。在此引入对偶理论[15-16]，以ωkt为变量，其最优解在不确定集的极值点处。通过应用大M 方法线性化[17-18]，得到混合整数规划问题（mixed integer programming，MIP）：

式中：，为线性化主问题（式（1）所示目标函数）时，应用Big-M 算法引入的参数变量，用于对非线性变量的近似；xb*it的取值范围为[0，1]，以满足最优解的取值；为在线性化转化中引入变量，作用是将主问题中火电机组的上、下爬坡速率、切负荷的系数进行线性转化；pb*it为t时段机组出力的最优解；dtotalt为t时段内系统的总负荷为在线性化主问题时，应用Big-M算法引入的参数变量，用于对线路传输约束的线性化。

约束条件如下：

1）大M算法约束：

式中：Mbig为Big-M 算法中人工引入变量；bkt的取值范围为[0，1]，其作用是约束M值。

2）弃风成本约束：

式中：为线路l上风电场k弃风的成本系数。

3）切负荷成本约束：

上述可行域为CCG 算法求解后，最优结果所在的集合，而其中的最优解为满足约束条件（式（19）～式（23））下的系统目标函数（式（24））中的决策变量。

CCG算法流程图如图2所示。

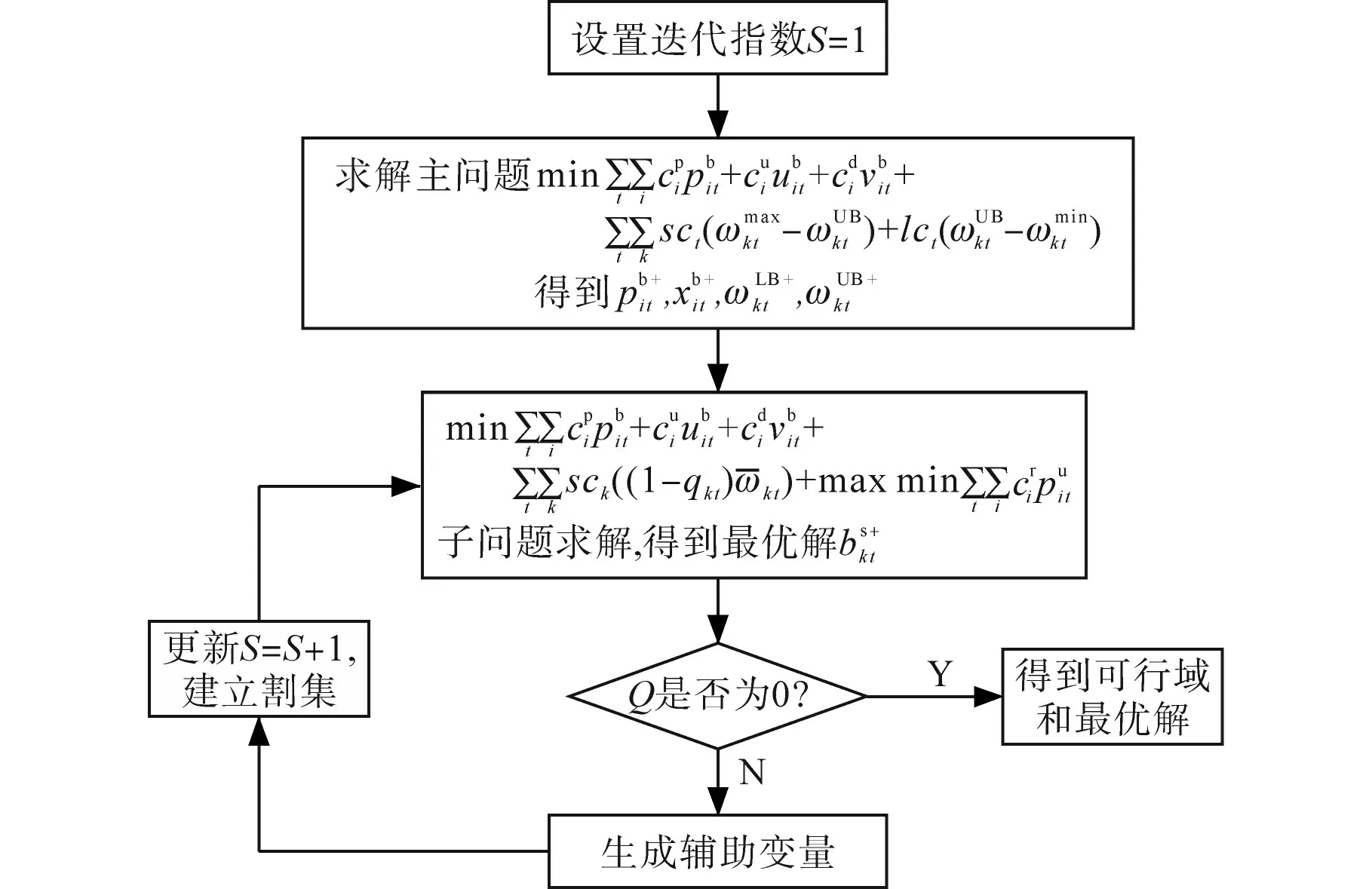
图2 CCG算法流程Fig.2 Flow chart of CCG algorithm

4 结果分析

为了验证所提出的电力系统灵活性定量评估框架的可行性和有效性，在改进的IEEE RTS 24 测试系统上进行了数值模拟[19]，发电机数据和测试系统的负荷数据如表1和表2所示，在节点1处接入风电渗透率为20%的风电场[20]，α和β分别设置为0.8 和1.2[21]。利用Cplex 求解器对所提出的模型进行求解。

表1 IEEE RTS 24节点系统发电机组参数Tab.1 Parameter of generators in IEEE RTS 24 bus system

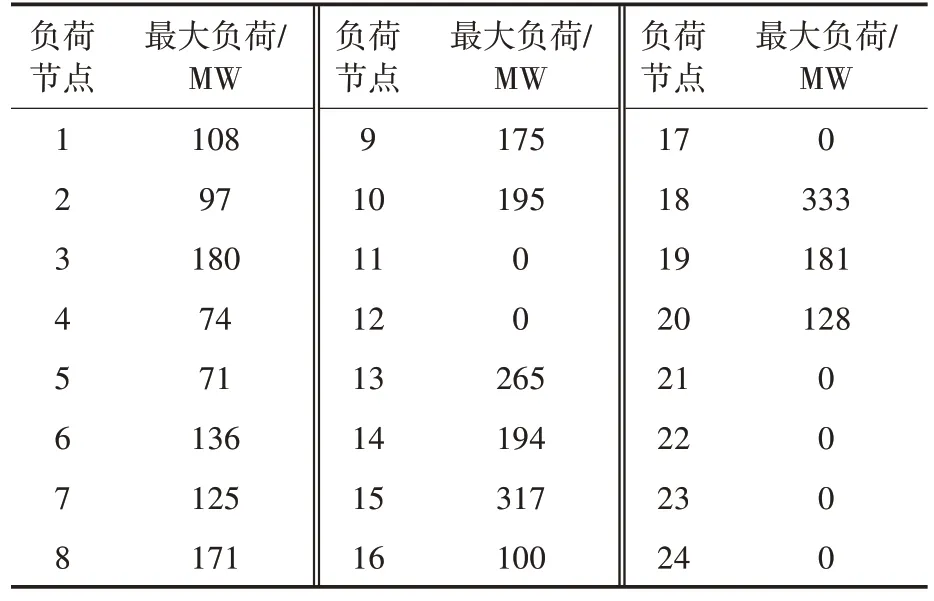
表2 IEEE RTS 24 节点系统各节点最大负荷Tab.2 Maximum load for IEEE RTS 24 bus system

以预测的风力发电不确定性集（20%的变化）为输入，应用所提出的鲁棒模型来描述系统所能适应的最大不确定性区间。切负荷和弃风惩罚系数分别设定为1 000 ＄/（MW·h）和100＄/（MW·h）[22]。图3 描绘了风电功率不确定性最优集和预测不确定性集的上界，由于惩罚值lck较高，不确定性集的最优下界和预测下界相等。然而，最佳上限低于17 h，22 h 和24 h 的预测上限，表明系统缺乏足够的灵活性能力来响应以上时段内设置的预测不确定性。这主要是因为观察到该时段内的净负荷为负，导致发电机组提供向下运行备用的能力较低。

图3 风电功率不确定性最优集和预测集上界Fig.3 Upper bound of optimal set and prediction set of wind power uncertainty

图4 为系统备用需求，系统提供运行备用的能力可以在发电机组容量、爬坡能力以及输电限制不存在不确定性的情况下，考虑发电机组的输出功率确定，预测不确定性集合满足所需的备用容量。如果提供的备用大于所需备用，电网将保持安全运行。

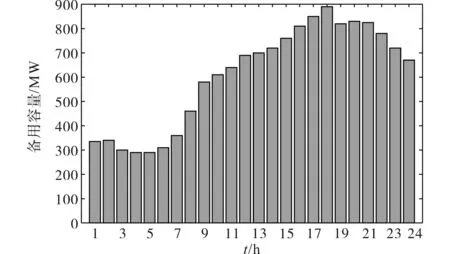
图4 系统备用需求Fig.4 Diagram of system standby demand

图5为发电机组提供的下行备用和根据不确定性集的预测上限和预期风力发电之间的差异实现的所需备用。可以看出，22 h 和23 h 的所需储备高于所提供的储备。因此，最优上限值被视为低于预先设定的上限值，并且不确定性区间被缩小以减少所需备用量。

为了比较本文两阶段鲁棒模型中可调不确定度集合的作用，将其与不可调不确定集合[23]做对比，如表3所示。在可调不确定性集合中，本文假设风力发电量在第一阶段是固定的。结果表明，在这两种不确定集合下，本文的CCG 算法都具有可求解性。这是因为预定义不确定性集合的最坏情况灵活性要求未超出系统发电机组的灵活性容量，因此，可以有效处理最坏情况下的风电接入容量问题。利用CCG 算法，在每次迭代中嵌入不带松弛变量的割集，使得系统发电机组的输出功率得到修正，即使在最坏的风电情况下，也能满足功率平衡和输电线路约束。在灵活性能力不足的情况下，只有将主问题中的不确定性集合作为变量考虑，使不确定性区间缩小，CCG算法才有可行的解。

表3 不同不确定集合的系统成本比较Tab.3 Cost comparison of different uncertain sets

从表3 中的数值对比角度来说，在发电机组缺乏足够的灵活容量的情况下，通过弃风或切负荷能实现安全运行。由数据可看出，可调鲁棒不确定集合模型下的切负荷成本小于不可调鲁棒不确定集合模型下的切负荷成本，而弃风成本大小关系则相反。综合考虑系统运行的安全性、经济性和灵活性等多方面因素，采取可调鲁棒不确定集合的方法，能实现最优的调度决策。因此，在保证系统安全的前提下，相较于弃风成本系数来说，切负荷的成本系数更高，可调鲁棒集合更具有灵活调整的功能，这使得此模型能取得更小的运行成本和总成本。

预期风力发电的最佳利用率（即最佳渗透率）在17 h，18 h，22 h 和23 h，风电场的总渗透率分别为94.94%，97.36%，97.74%，99.08%，低于100%，因此出现了弃风现象。由于风力发电量较高，17 h 和18 h 的不确定区间间隔较高，因此风力穿透率低于100%以减小不确定区间间隔，从而使系统能够有效应对不确定度。22 h 和23 h的渗透率较低是因为这个时间的净负荷处于最低水平，发电机组以较低的功率输出进行调度，其向下爬坡能力降低。因此，随着风渗透率的减少，净负荷增加，发电机组向下爬坡的能力将增加。在其他时间，总渗透率均为100%。

5 结论

本文提出了一种基于两阶段鲁棒优化方法的电力系统运行灵活性评估模型。模型第一阶段，假设可再生能源出力是确定的，以系统运行成本、弃风、切负荷最小化为目标函数；模型第二阶段，考虑可再生能源出力的不确定，对模型第一阶段的运行调度策略进行调整，针对可再生能源出力的不确定因素，构建一类可调的鲁棒集进行刻画。采用对偶理论和大M 法对模型进行转化，使之成为具有可解析形式的优化模型。采用CCG 算法对模型进行求解，在改进的IEEE RTS 24 节点测试系统上通过数值模拟验证了所提评估方法的有效性。研究得到以下结论：

1）通过与不可调鲁棒模型比较，系统仿真数值结果表明了所提可调鲁棒模型的有效性及优越性。较传统不可调鲁棒模型，所提可调鲁棒模型能有效降低系统运行成本，减小其调度决策的保守性，进一步提高系统调度决策的灵活性和经济性。

2）不确定的风电出力影响机组的灵活性调度，以弃风和切负荷来评估旋转备用容量的预调度的灵活性，可有效提高系统运行调度的性能。