基于PCA-BP神经网络的输电线路工程投资概算模型研究

王林峰，徐楠，聂婧，谢延涛，宋妍

（国网河北省电力有限公司 经济技术研究院，河北 石家庄 050000）

随着我国电力体制改革的不断推进[1]，输配电价改革要求电网企业成本控制更加精益化[2]，传统成本管理已不能适应新形势。按照电网建设“三年行动计划”，2020 年河北省公司输电线路工程开工、投产规模再创历史新高，高质量电网发展需要高质量技术经济管理作为保障。电网公司进行造价管理过程中主要使用结余率作为主要指标。现阶段的电力公司在进行电网线路工程投资管理时，结余率基本偏高，使得工程结算价与合同价差异较大[3-4]。因此，需要通过输电线路投资估算模型预测投资，协助技术经济管理人员快速评估造价，确认方案合理性，提高工程造价管理效率。

传统的工程投资预测方法分为定性[5-6]和定量[7-8]两种。定性预测方法主要有专家会议法、德尔菲法和主观概率法。定性预测法具有收集专家意见和期望的特点，过程繁琐，不可避免地会引入专家的主观因素。定量预测方法包括移动平均法、指数平滑法、趋势外推法、卡尔曼滤波法、灰色预测法等。定量预测方法不受主观因素影响，但对于复杂工程项目而言，原始数据复杂多样、数据规律性差、难以处理数据间交互作用和非线性关系等劣势也限制了其进一步应用[8]。

针对传统预测方法存在的缺陷，国内外学者提出了一些新的工程投资预测算法[9-10]。为了解决输电线路工程投资预测方法准确性低、工作量大等问题，卢文飞等人[11]提出了基于极端梯度提升算法的输电线路工程投资预测方法。所提方法在预测精度、结果偏差方面相较于神经网络和支持向量机（support vector machines，SVM）都具有显著优势，可为决策者提供有效的数据参考。赵晓芳等人[12]将随机森林算法、粒子群算法和SVM 相结合，建立了输电线路工程造价预测模型，收集实际数据组成数据集，利用分类树给出分类范围，利用粒子群算法确定支持向量机参数的范围，得到最优SVM 预测模型，进行有效预测。孙安黎等人[13]提出了一种基于BP 神经网络的输电工程造价预测模型，受限于BP 神经网络优化目标函数的复杂结构，预测结果容易产生“之字形”现象，在实际应用中容易产生误差。

针对现有输电线路投资估算方法存在的问题，提出了一种基于PCA-BP（principal component analysis and back propagation）神经网络的输电线路投资预测方法。融合主成分分析法（PCA）与改进BP 神经网络算法在数据处理与预测方面的突出优势，对分析的维度进行降维处理，提高计算与预测效率。实例分析结果验证了所设计基于PCA-BP 神经网络算法的输电线路工程投资概算模型的正确性、可行性及有效性，为设计方案的甄选提供有力支持。

1 PCA与改进PB神经网络算法

1.1 PCA方法

PCA 的核心思想是降维，其通过进一步提炼和整合模型指标的分散化信息，得到最关键的信息内容，便于从大量原始信息中剔除冗余信息，其原理是将原有多个具有一定相关性的指标[14]重新组合形成较少个数且相互间不存在相关性的主成分指标[15]。假设有N个样本，每个样本有P个指标，则原始矩阵为XN×P=[xij]N×P，主成分分析过程如下：

由于对输电工程投资进行概算的样本存在个体性，各个指标单位之间存在差异性，为消除原始变量量纲不同及数值差异巨大可能产生的影响，利用下式对原始数据进行标准化处理：

标准化处理之后得到标准化矩阵：

构建标准化矩阵Z的相关系数矩阵R：

其中

式中：cov(Zi,Zj)为Zi和Zj(i,j=1,2,…,P)的协方差。

求解相关系数矩阵R的特征值及特征向量。若相关系数矩阵R有q个非负特征值λ1,λ2,…,λq，且λ1≥λ2≥…≥λq，则其相应的规范正交特征向量为A=[a1a2…am]，m个主成分为

其矩阵表达式为Y=ATZ。

计算方差贡献率ηi及累计方差贡献率ηΣ(p)，确定主成分个数。

主成分个数的判定需要借助累计方差贡献率ηΣ(p)，一般情况下累计方差贡献率大于75%时，此时对应的p即为主成分个数，前p个主成分所含信息基本可代替原始数据信息。

1.2 改进BP神经网络算法介绍

BP 神经网络，即误差反向传播网络，是一种多层前向网络，其典型结构图如图1所示，其中节点代表神经元，箭线代表其连接关系。BP神经网络结构可分为输入层、隐含层和输出层3层，不同层内节点之间没有连接关系，前后层节点间存在前向全互连关系[16]。BP 神经网络的学习训练过程包括正向传播和反向传播两部分。正向传播过程中，向输入层输入原始信息，传递至隐含层进行处理，最终输出层输出结果。计算输出值与期望值之间的误差，当误差超过要求时，误差信息将进入反向传播过程，沿原通路反向传递并修改通路上的层间权值，直到误差满足要求，训练过程结束。经过训练的BP 神经网络模型可用于求解同类问题[17]。

图1 BP神经网络典型结构图Fig.1 Typical structure of BP neural network

图1中，Wi(i=1,2,…,5)表示网络中输入层的输入节点，hj(j=1,2,…,11)表示隐含层的节点，TE表示输出层的节点。输入层与隐含层的连接权值为ωij，隐含层与输出层之间的连接权值为ωjk。

传统BP 算法采用下降规则搜索最优算法，没有考虑前一阶段积累的经验，导致训练过程产生震荡，从而影响收敛速度[18]。基于BP网络梯度下降规则，通过改进BP 网络权值和学习率，对BP网络权值和阈值进行初始化，调整适应误差下降的要求。当输入样本按神经网络结构顺序输入时，针对改进BP 神经网络结构的隐含层节点数及层数进行优化设计。

采用相关性剪枝算法，根据网络节点间相关性进行剪枝。对隐藏节点之间的相关性进行判断，对其中相关性较大的节点进行合并处理。当隐含层节点的输出标准差较小时，可以直接将该节点输出过程看做常数输出过程，直接转移到下一层的偏移节点，并将具有较大相关性的隐含层节点进行合并，成为一个节点。

将tansig 函数作为激活函数对隐含层节点输出之间的相关度进行计算。在隐含层中，假设第ci个节点与第cj个节点对n个样本的输出序列分别为{Vcin}和{Vcjn}，对应的均值分别为和。对应的相关性的计算公式为

对隐含层节点输出之间的输出方差进行计算，第ci个节点与第cj个节点之间的误差计算公式如下：

当节点ci与节点cj之间的输出方差较小时，可认为其中一个节点的输出值为固定值。将剪枝后的结果，通过经验在学习训练过程中不断地调整隐含层节点数，最后得到一个合适的网络结构。

2 基于PCA-BP 神经网络的输电线路工程投资概算模型

融合前文所述PCA 和BP 神经网络的在数据降维及模型预测方面的突出优势，本文提出并建立了基于PCA-BP神经网络的输电线路工程投资概算模型，所提模型的实现路径如图2所示。

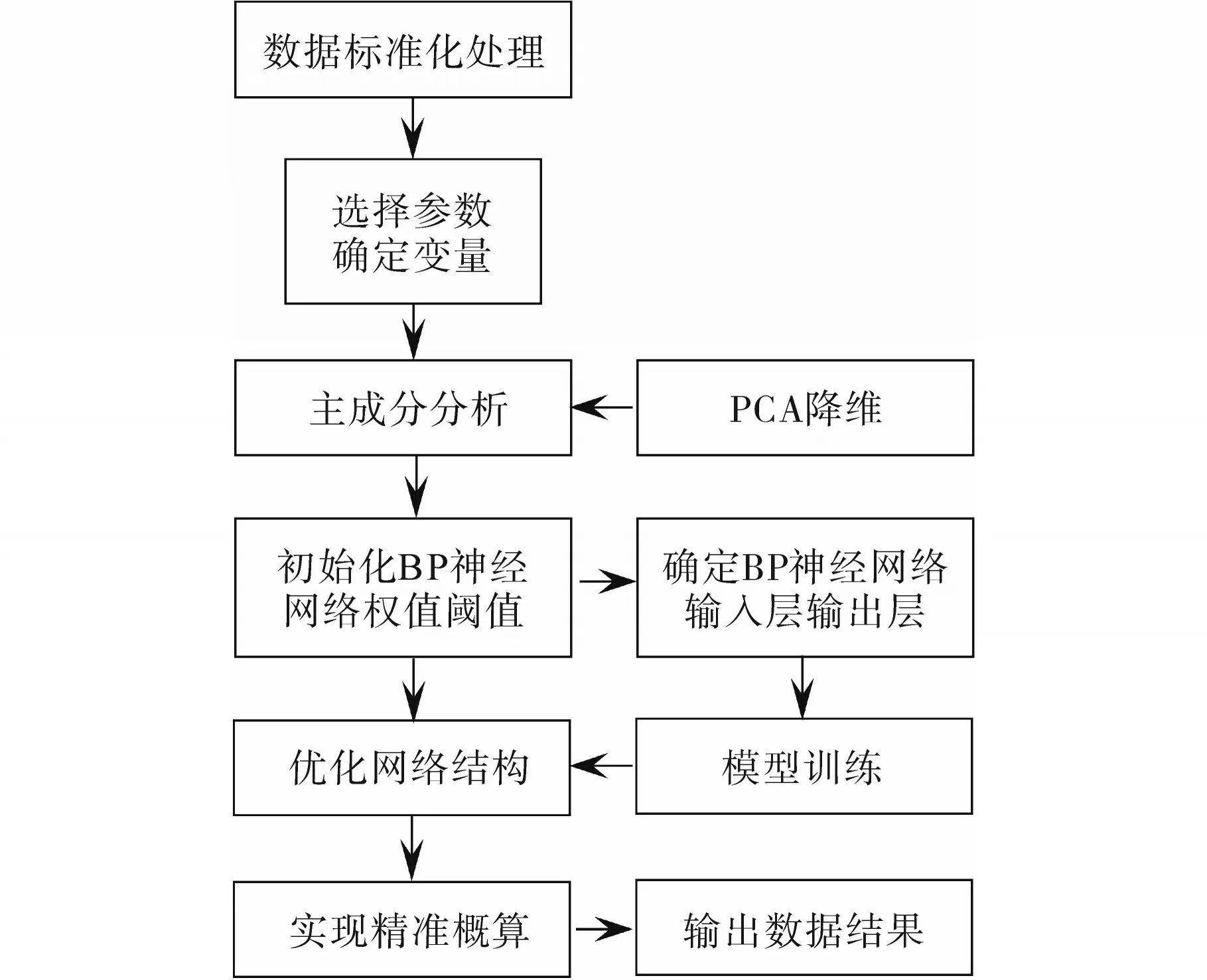
图2 基于PCA-BP神经网络的输电线路工程投资概算模型流程图Fig.2 Flow chart of transmission line project investment estimation model based on PCA-BP neural network

所提基于PCA-BP神经网络的输电线路工程投资概算模型可根据输电线路工程的特征，选定对投资概算预测结果影响较大的参数作为模型的初始输入变量。之后，借助PCA 对初始输入变量进行分析并降维至少数主成分变量。将PCA所得的结果作为BP 神经网络的输入节点，对BP神经网络进行网络结构优化。PCA 的引入有效减少输入节点个数的同时优化了BP 神经网络的结构，从而加快其收敛速度，实现对输电线路工程投资的高精度概算。

2.1 初始输入变量的选取

输电线路主要用于输送电能，实现各发电厂、变电站（所）间的并列运行与电力系统间的功率传递。实际应用场景要求输电线路工程具有投资成本低、建设周期短等优势。结合专家评定结果和实际案例分析，对所建立的输电线路工程投资概算预测模型在构建时主要采用电压等级、折单长度、回路数、导线参数、地形情况、覆冰厚度、设计风速、单千米导线重量、单千米地线重量、地线价格、导线价格等作为造价成本的主要影响因素展开分析。

2.2 初始输入变量的主成分分析

BP神经网络要求输入数据为实数，而输电线路工程电压等级、回路数、导线参数及地形情况4个变量为文字表述或多维度参数，为便于后续计算，须对上述4 个变量参数进行处理。所遵循的数据处理原则如下：

1）对样本中的电压等级数据进行筛选，发现其数据均表现为交流电形式。因此删去电压等级数据的交流及kV 单位的描述，仅保留数字作为该变量的样本数值。

2）输电线路中的回路数1，2，3分别表示单回路、双回路、三回路。当线路包含多种回路数时，以最长的回路数为主。

3）对于地形状况这一变量，按照相关地形系数计算规则将平地、丘陵、山地、高山、峻岭等地形参数统一转化为综合地形系数进行表示。描述不同地形特征的地形参数主要有坡度、坡长、地形起伏度、地表切割深度及单位汇水面积[19]。

坡度可表示为

式中：fx，fy分别为x和y方向的高程变化率。

坡长表示为地面上任意点沿水流方向到其水流源点的最大地面距离在水平面的投影长度：

式中：Lw为水流长度。

地形起伏度表示为分析区域内最大高程Hmax与最小高程Hmin的差值：

地表切割深度表示为地面任意点的领域范围内平均高程Hmean与最小高程的差值：

单位汇水面积表示为流域面积A与流域宽度（等高线线段长度Ld）的比值：

求得每一地形对应上述几个参数的数值后，确定综合地形参数，用于后续计算。

4）导线参数这一变量的各个数据中最为重要的是导线型号。然而因导线型号描述为文字性描述，采用导线截面作为参考数值进行计算。

通过对各变量参数的方差贡献率进行计算并借助PCA 算法对数据进行降维处理，将得到的电压、导线参数、地形、风速、单千米导线重量、单千米地线重量、地线价格、导线价格和单位造价用作后续的预测模型的输入变量。

2.3 改进BP神经网络的输出层、隐含层确定

现有理论表明3 层BP 神经网络具备映射任意复杂非线性函数关系的能力，已成功应用于多个领域的变量预测。在前文通过PCA 对BP 神经网络结构改进优化的基础上，所建立的输电线路工程投资概算预测模型选择3 层BP 网络作为底层结构，设置输入层神经元个数为9，输出层神经元个数为1，用于输出输电线路工程的单位造价参数。此外，构建改进的投资概算预测BP 神经网络模型时，分别选取隐含层神经元个数为10，15，20 及25 进行训练、比较和分析，从而确定满足精度指标需求下更为合理的隐含层神经元数目。训练结果显示隐含层节点个数为15 时的误差最小，预测准确度最高，因此选取隐含层神经元个数为15。通过PCA 算法与改进BP 神经网络算法的结合，实现对输电线路工程投资概算模型的构建与高精度预测。

3 实例分析

3.1 样本数据来源

为了提升结果的可参考价值，文章所用研究数据参考“河北省2018 年01 月—2020 年01 月实际输电线路工程概算文件”，包含项目造价及技术技经指标数据等。依据上文确定的研究思路，首先消除因初始输入变量的量纲及数值差异的影响，对样本数据进行标准化处理。样本总数取为50，正数表示数据高于标准化结果，负数表示数据低于标准化结果。部分数据如表1 和表2所示。

表1 样本数据标准化结果Tab.1 Standardization results of sample data

表2 地线导线数据结果Tab.2 Ground wire data results

3.2 预测模型的建立

利用PCA 方法降维的方差贡献率结果如图3和图4所示。通过PCA算法对初始输入变量数据进行降维处理，计算各个参数的方差贡献率ηi。当累计方差贡献率ηΣ(p)大于75%时，所得参数即为主成分。确定为主成分的变量代入后续的BP神经网络算法进行训练。

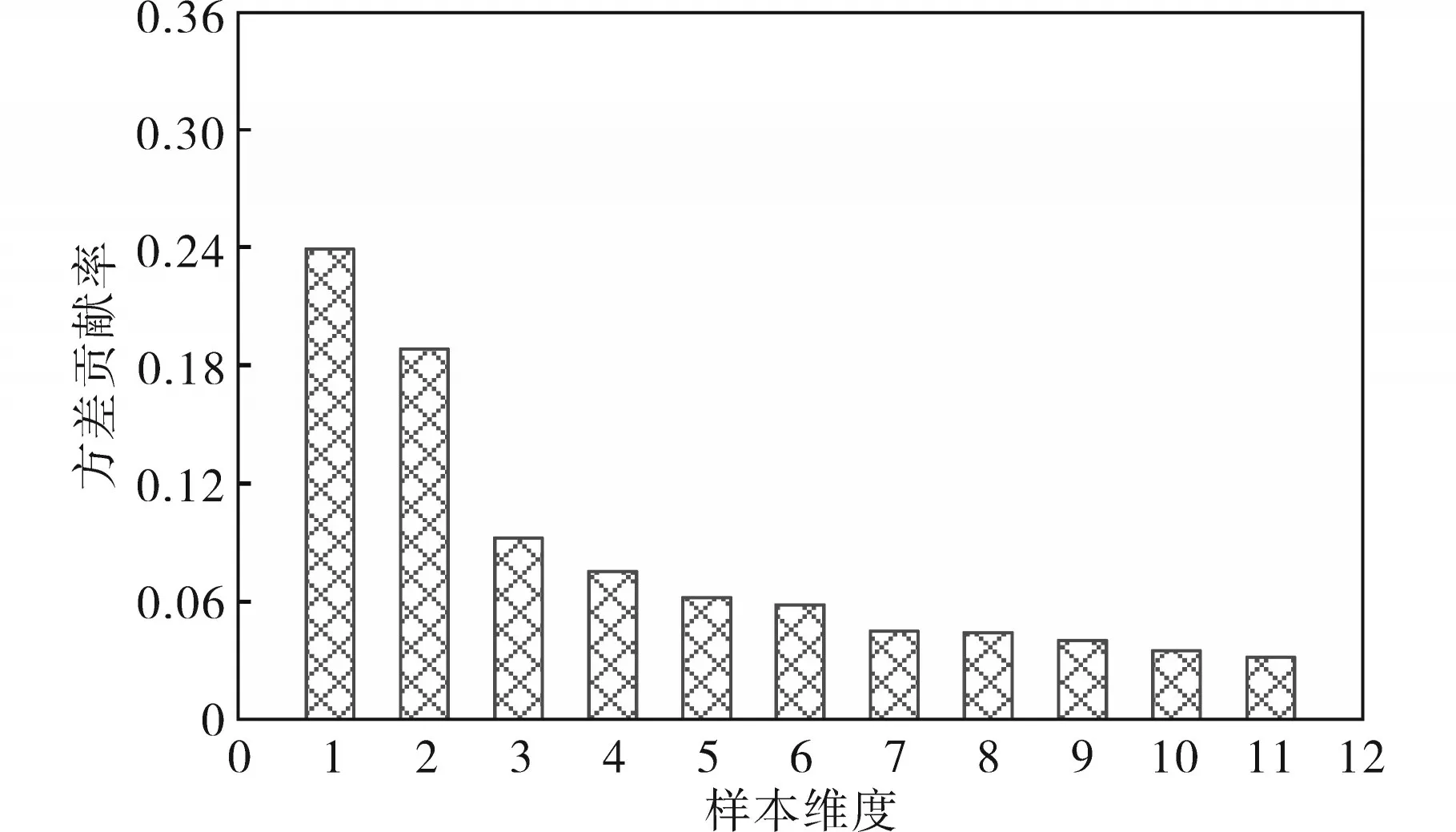
图3 不同样本维度时的方差贡献率Fig.3 Variance contribution rate under different sample dimensions

图4 累计方差贡献率达标情况Fig.4 Compliance of cumulative variance contribution rate

对于PCA 算法而言，贡献率表示为贡献量（产出量、所得量）与投入量（消耗量、占用量）的比值，用于分析各因子作用大小的程度。方差贡献率常用于表示单个公因子引起的变异占总变异的比例，说明此公因子对因变量的影响；而累计方差贡献率用于表示所有公因子对因变量的合计影响力。不同维度下的方差贡献率不同。因此，参考图3和图4的结果，当维度为7时，累计方差贡献率ηΣ(p)为75.61%，此维度下系统的输出结果满足设定条件。因此，经过PCA 计算之后，将参数的最终维度由10 降至7 即可满足需求，从而有效提高后续BP 神经网络的训练效率与模型预测精度。

将表1 所示的50 组项目数据作为样本，使用随机梯度下降（stochastic gradient descent，SGD）优化算法训练网络。SGD 算法主要用于优化系统的目标函数f( )θ，求得最小化的目标函数值。SGD 算法的参数更新过程简单、高效，且实际迭代成本独立于样本数据库。通常利用θ的梯度∇θf(θ)的反方向对θ进行迭代更新，每轮更新时仅随机抽取一个样本并计算其梯度，以该值作为全局梯度的估计值[20]。SGD的参数更新公式如下式所示：

式中：αt为学习率；t为第t轮迭代中按均匀分布随机抽取的样本序号，t∈{}1,2.…,n；∇ft(θt)为样本对应的梯度值。

通过学习率可变的动量梯度下降算法修正神经网络的权值与阈值，设定最大循环次数为3 000；目标误差为0.01；初始学习速率设为0.02。经过1 420 次训练，训练误差小于0.01，达到预测精度要求，训练结束。训练误差曲线如图5 所示。

图5 训练误差曲线Fig.5 Training error curve

3.3 预测结果与分析

为了验证所训练神经网络模型的预测精度，使用表1 中的后50 组数据对神经网络精度进行测试，开展输电线路工程概算投资的预测分析。同时，为了体现所提基于PCA-BP 的输电线路工程投资概算预测模型的优越性能，选择文献[10]提出的SVM 预测模型与文献[11]提出的BP 神经网络模型作为对比进行分析。随机抽取10 个项目进行工程概算投资预测以消除人为主观因素对模型误差测试结果的影响。此外，为了清晰表达不同概算预测算法所得到的预测结果与实际值之间的误差，文章根据相应数据计算了不同方法的预测结果与真实值的误差大小和预测准确率，所得结果如表3所示。

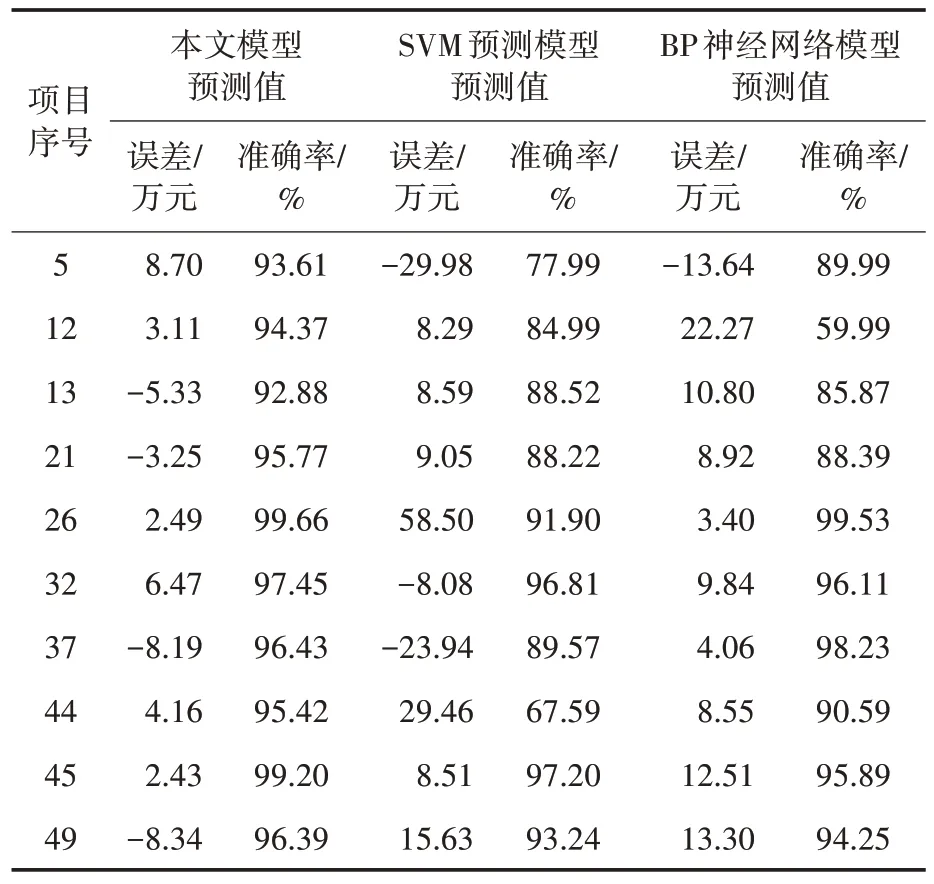
表3 不同方法的工程概算投资预测结果Tab.3 Project budget and investment prediction results of different methods

分析表3 可知，在随机抽取的输电线路工程投资概算预测结果中，基于SVM 模型的预测值与实际造价之间的误差波动较大，预测准确率范围为67.59%～97.20%。基于BP 神经网络模型预测值与实际造价之间的误差波动同样较大，准确率为59.69%～99.53%。本文模型预测值的准确率高达92.88%～99.66%，与实际造价之间的误差波动相比SVM 和BP 神经网络有了明显改善，符合相关管理规范要求（3%～5%）。不难发现，文章所建立的输电线路工程投资概算预测模型在预测准确度及稳定性方面具有突出优势。为了验证所建立输电线路工程投资概算预测模型在综合预测性能方面的优势，文章对上述3 种不同模型预测算法在实际预测过程中的收敛速度（达到目标误差所用时间）进行对比，如图6 所示，并从鲁棒性、稳定性、自学能力以及反应速度等角度对比了SVM、传统BP 控制的优势，具体对比如表4所示。

表4 所提算法与SVM、传统BP算法的性能对比Tab.4 Performance comparison of the proposed algorithm with SVM and traditional BP algorithm

图6 不同模型收敛速度对比Fig.6 Comparison of convergence rates of different models

由图6 可知，文章建立的概算预测模型相比于SVM 及BP 神经网络具有最快的收敛速度，达到目标误差所需的时间始终保持在0.6 s以下。

从表4中可以看出，传统BP 可实现非线性映射，有自学能力和推广概括能力，但由于其采用梯度下降法，速度慢，有可能进入局部最小值而训练失败，对新加入的样本有影响，可能会出现欠学习或过学习；SVM 算法是基于非线性映射理论，其利用核函数代替了高维空间的映射，最大化间隔是核心，支持向量是训练的结果，最终结果是少量的向量决定的，可以提出较大的样本，但由于其鲁棒性偏弱，对大规模训练难以实施，解决多分类有很大的困难；本文所提PCA-BP 算法的鲁棒性较强，其稳定性也高于传统BP 算法，可以有效提高系统的预测模型的准确性，同时提升该模型的反应速度。

因此，所建立的输电线路工程投资概算预测模型具备在给定样本数据下的概算快速、准确预测的能力，有效提高了概算管理的工作效率，具有显著的实际应用价值。

事实上，考虑到启发式学习算法误差的不可避免性，实际预测分析与应用时，应对样本展开多次平行分析并取预测结果的平均值作为最终预测结果，从而进一步提升概算预测模型的输出结果的可靠性与准确性。

4 结论

输电线路工程是连接电源和受电用户的重要网架基础，是电力输送和使用中不可或缺的重要环节。针对目前输电工程造价概算预测方法误差较大的问题，本文建立了基于PCA-BP 神经网络算法的输电线路工程投资概算预测模型。通过对输电线路工程造价关键影响因素的PCA与模型训练，实现了对输电线路工程造价的概算预测。以某地若干历史输电线路工程投资概算资料为样本，分析了典型预测方法的模型准确度及收敛性能。预测结果分析过程中对比了所提算法与传统BP 算法、SVM 算法的性能，突出所提PCA-BP 算法的整体优异性。结果验证了本文所建立输电线路工程投资概算预测思路的正确性、可行性及有效性，预测准确率高达92.88%～99.66%。

考虑到愈发复杂和变化多样的工程环境，所提预测模型为输电线路工程的造价管控提供了全新思路，对输电线路工程的方案必选提供了有力支撑。在后续研究中，将着重于数据的聚类计算，进一步降低预测误差，获得性能更为优良的综合预测模型。