基于CBAM-CNN的直流线路雷击干扰与短路识别模型

廖志伟，庄竞，王博文，郑广昱，谢汛恺

（华南理工大学 电力学院，广东 广州 510641）

高压直流输电（high voltage direct current，HVDC）工程的输电线路较长，雷击和短路故障频发。然而当前的行波测距装置并不具备识别雷击干扰与短路故障的功能，非故障性雷击容易导致测距装置误动作[1]。准确地识别线路雷击干扰与故障对于提升HVDC的运维水平具有重要意义。

目前对于雷击与短路识别的研究主要基于提取波形的时域、频域特征[2]。时域法关注波形变化趋势特征，文献[3]将雷击或故障前、后电流的变化量作为特征，但雷击后一段时间内行波存在折反射过程，且故障行波也可能存在过零点，可靠性不足；文献[4]提出以时间轴上、下方波形的积分值作为判据，但受母线结构影响较大；文献[5]分析了地模、线模附加分量波形变化特征并以幅值、幅值比与变化率组成雷击干扰识别判据，但该算法的抗噪能力并未得到验证。频域法则使用小波变换[6-9]、广义S 变换[10]、希尔伯特-黄变换[11-12]等时频分析工具揭示频域特征，构建识别判据。其中基于小波变换求取能量分布特征是故障识别领域应用最多的技术路线，而具体判据的选取则存在不同的方案。文献[6]提出根据主分量能量占比的差异识别雷击与短路故障；文献[7]基于小波变换的多分辨分析，将小波熵组成特征向量用以区分；文献[8]把小波分解得到的高低频能量比值作为判别依据，但在极端情况下的部分雷击干扰与短路故障的能量高低频分布特征相似，容易误判[1]；文献[9]则将高频段能量占比是否达到阈值作为判据，但基于单一频段能量的判据易受故障和雷击参数影响。

以上研究均基于故障机理分析设计典型的特征判据以区分故障类型，但存在阈值整定困难的共性问题，且识别灵敏性易受噪声等因素的影响。此外文献[1]指出使用单一的指标判据难以进行可靠、有效的雷击干扰与短路故障识别。另一方面，文献[13]也指出电力系统故障机理逐渐展现出多因素耦合、随机性增强等特征。以卷积神经网络（convolutional neural network，CNN）为代表的深度学习方法具备特征自提取和强非线性拟合能力且可实现自动分类，解决了传统方法需人为分析和构造特征、阈值设定困难的问题，在故障识别领域具有良好应用前景。

目前深度学习方法在雷击识别上的应用较少，文献[14]分别提出使用CNN 识别雷击与短路故障行波的时频图，文献[15]提出利用深度残差网络识别雷击跳闸暂态信号经广义S变换得到的时频分布图。上述研究仅对原始信号进行简单转换处理后输入至深度学习网络即可得到令人满意的识别效果，然而用于处理和识别二维时频图像的神经网络的参数量和计算量远大于处理一维数据的网络，训练网络占用的硬件资源较多、计算速度较慢[16]。

针对上述问题，本文提出在对行波进行时频分析的基础上，使用更加轻量化的一维CNN 模型识别雷击干扰与短路故障，同时加入注意力机制模块以提升识别模型的性能，并通过仿真试验验证了本文所提模型的泛化能力、噪声鲁棒性相比传统算法的优势，并研究了时频分析算法和参数的选取对模型性能的影响。

1 CBAM-CNN模型

1.1 卷积神经网络

卷积神经网络能够自主地提取和学习蕴含在数据内的特征，对于一维时间序列、二维和三维图像数据均适用。由于在直流线路故障分类模型当中，CNN 需要处理的数据均为一维的暂态行波时域数据，本节对一维CNN 进行介绍，其结构如图1所示。

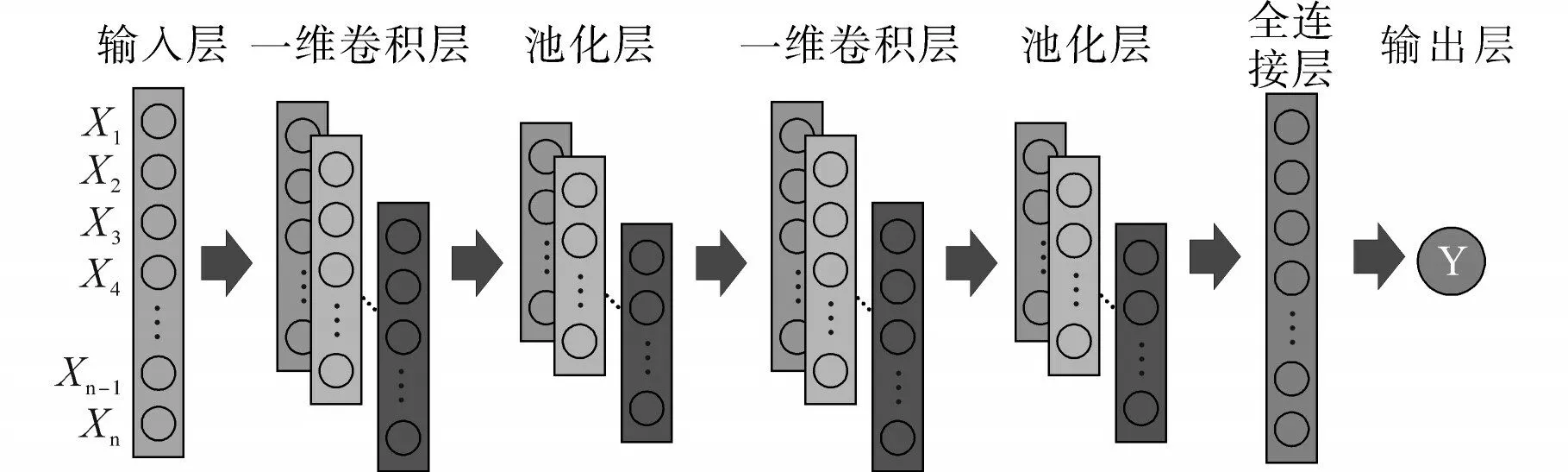
图1 一维卷积神经网络结构图Fig.1 Structure diagram of 1D-CNN

图1 中，输入层为波形时间序列{X1，X2，…，Xn}。每个卷积层均包含了若干个卷积核，图1 中不同颜色的层代表了输入层数据经多个卷积核运算后得到的多输出通道序列。卷积核实质上是神经网络的共享权值，在时间序列上沿着时间轴滑动，并与对应区域的波形时序数据做卷积运算。

1.2 卷积模块注意力机制

时间序列或图像上并非所有信息都有助于CNN 的学习任务，对更有效的信息赋予更高的关注度可有效提升模型学习效率和效果。卷积模块注意力模块（convolutional block attention module，CBAM）是一种应用于前馈卷积神经网络的轻量化模块，结合了空间注意力机制和通道注意力机制。CBAM 本质上是在这两个维度上的加权机制，其应用于一维CNN 的结构如图2所示。

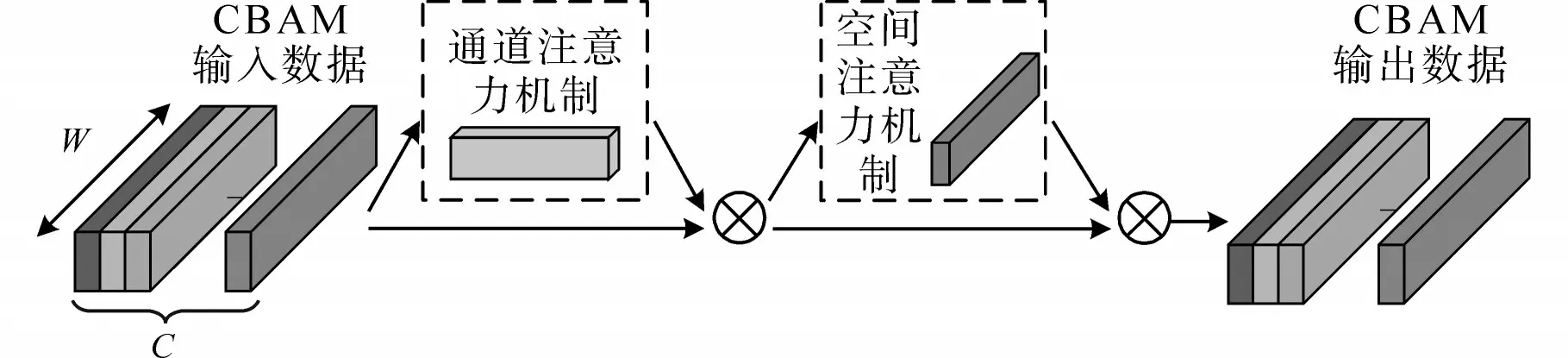
图2 CBAM模块示意图Fig.2 Schematic diagram of CBAM module

如图2 所示，CBAM 模块是按照通道注意力、空间注意力模块的顺序组合。CBAM 的输入是通道数为C、序列长度为W的多通道特征图，通道注意力机制沿着通道方向依次对输入数据分别进行全局最大池化和平均池化运算，分别得到两个C×1 的向量，随后由一个共享的多层感知器处理上述两个向量后将其相加，最后经过激活函数处理得到通道权重向量，通道注意力机制的表达式如下：

式中：F为输入特征图；MC（F）为C×1 的通道权重向量；σ为激活函数，一般选用sigmoid 函数；MLP为多层感知器；AvgPool，MaxPool分别为平均池化和最大池化。

将该向量与输入特征相乘，赋予各个通道数据不同的权重即可得到新的特征图。空间注意力机制的原理与之相似，沿着W方向逐个通道维度地进行最大池化和平均池化运算后得到两个1×W的向量，经一维CNN 处理后输出一个1×W的向量，经sigmoid激活函数计算后得到空间权重向量，最后将空间权重向量与中间特征相乘得到最终的新特征图。在CBAM-CNN 网络中，CBAM 模块添加在卷积层前面，对特征图的通道和空间给予不同的关注度，以作为CNN 提取特征前的预处理，提升学习效果。

2 故障识别模型构建

2.1 波形样本预处理

雷击和短路可以发生在HVDC 输电线路上的任意位置，雷电波形与短路过渡电阻等参数存在随机性，HVDC 运行过程中其功率输送水平也随调度指令而改变，这些因素均对波形产生影响。故障识别模型应当具有较强的泛化能力，即对于不同参数的直流线路雷击干扰和短路故障均有较好的适应能力、能够实现准确分辨和识别。为了提升模型的泛化能力，将样本输入深度学习网络前，需要以尽可能排除雷电绕击和故障点位置、直流系统传输功率等因素的影响为目标，对暂态行波波形样本数据进行预处理。

雷电绕击和短路故障点位置对于样本的影响主要在于行波传播至两端的时间差异导致的两端波形时间不同步。由于故障行波过程时长较短，若选取固定的时间窗口截取两端行波波形，则无法获取有效信息长度接近的波形。为了解决此问题并排除双极电磁耦合的影响，需对电气量进行Karenbauer相模解耦并选取行波到达时刻前后固定时长的波形片段组成故障类型识别模型的输入样本。以电流行波为例，截取两端电流行波如图3所示。

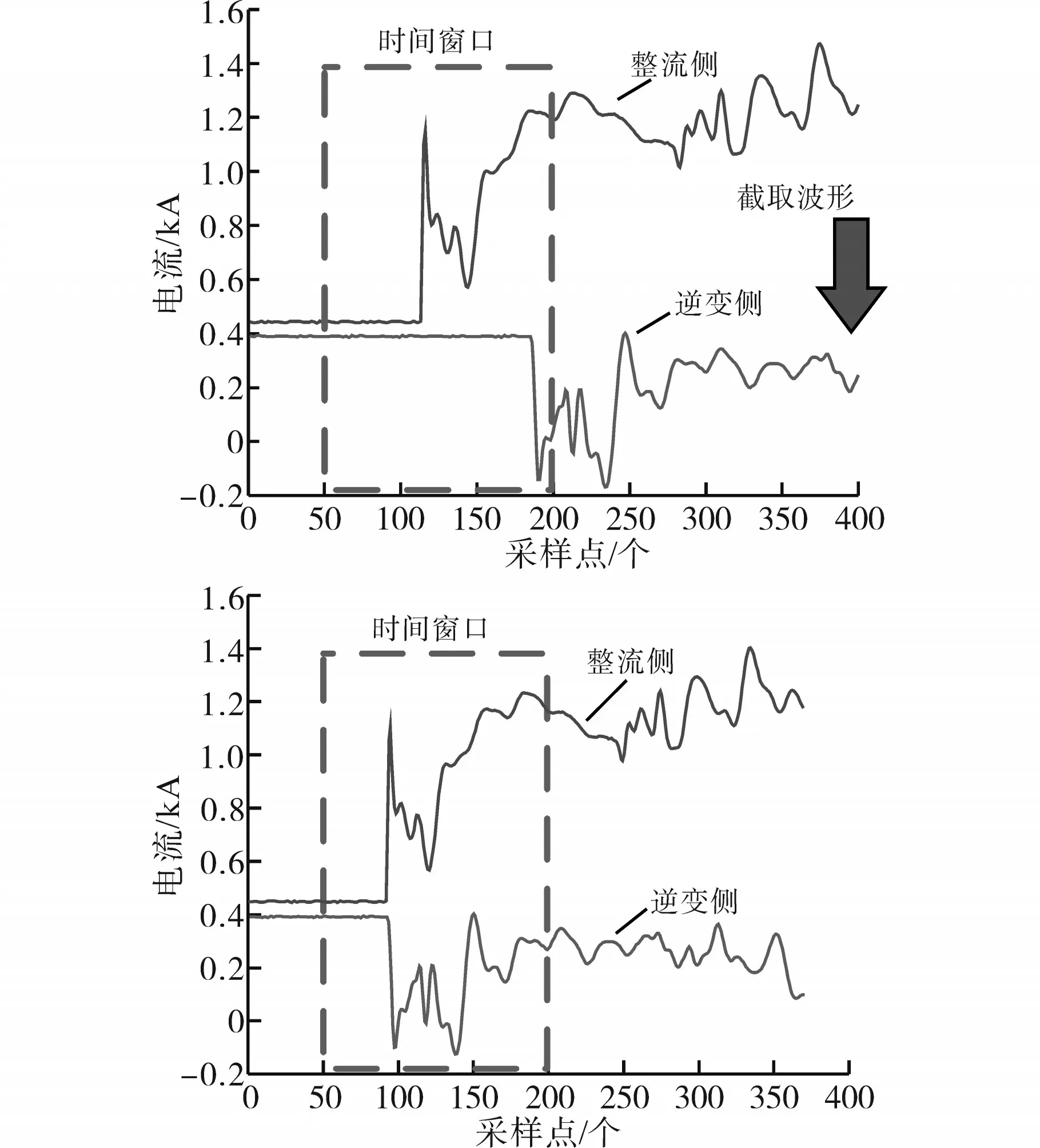
图3 电流行波截取Fig.3 Current traveling wave interception

直流系统传输功率水平发生变化时，由于系统参数并未发生变化，电流、电压行波仅幅值发生变化，且电流和电压也存在单位量纲的差异。为排除这一影响，可对行波进行归一化[17]。本文采用min-max 标准化方法，将全部信号的值映射到区间[0，1]之间，其转换公式为

式中：x（i）为原始信号时间序列；x'（i）为min-max标准化公式转化后的信号；min，max 分别为信号时间序列中的最小、最大值。

当信号幅值增大Δx时，有：

由式（3）可知，归一化处理消除了直流功率传输水平改变后波形幅值变化的影响。

2.2 时频特征构造

非故障性雷击电流低频分量的整体趋势变化相对短路故障较小，二者在频域上的能量分布等方面也存在差异。采用时频分析算法处理行波后，可同时展现波形在时域和频域上的特征，为神经网络分类模型输入较为全面的特征。

小波包分解（wavelet packet decomposition，WPD）适用于分析非平稳信号，且对于雷电干扰与短路故障行波等高频分量丰富的信号具有更好的时频分析效果。作为时频分析工具，连续小波变换与离散小波变换、小波包分解均可较为全面地获取波形在各个频带分布的信息。连续小波变换一般用于获取时频图[18]，离散小波变换和小波包分解、重构获得的不同频带的分量为时间序列，可使用一维CNN 进行分析，此时卷积网络更加轻量化，模型训练和诊断的速度更快。基于上述原因，本文使用小波包分解和重构得到的行波分量作为时频特征。

2.3 结合时频分析的CNN故障识别模型

小波包分解和重构作为对行波时频域特征的显式建模，输入至卷积神经网络可供其从时域和频域同时学习故障波形特征。本文所提故障识别模型将暂态行波的各个子频带分量波形作为输入数据的不同通道。CBAM 模块的通道注意力机制则为电流、电压故障行波的不同频带分量赋予不同的权重，空间注意力用于推断时域波形片段的注意力图。作为轻量化模块，CBAM 在不显著增加模型训练过程运算量的同时，可有效提升CNN 模型的可解释性和学习效率。卷积层采用4层一维CNN。在每两个卷积层之间，特征图需经过最大池化运算和ReLU 激活函数，分类器采用softmax作为激活函数。本文构建的结合时频分析的CBAM-CNN 故障识别模型流程如图4所示。通道注意力模块中多层感知器的两层神经元个数分别为32 和64，空间注意力模块卷积核长度为7，CNN网络的主要参数如表1所示。

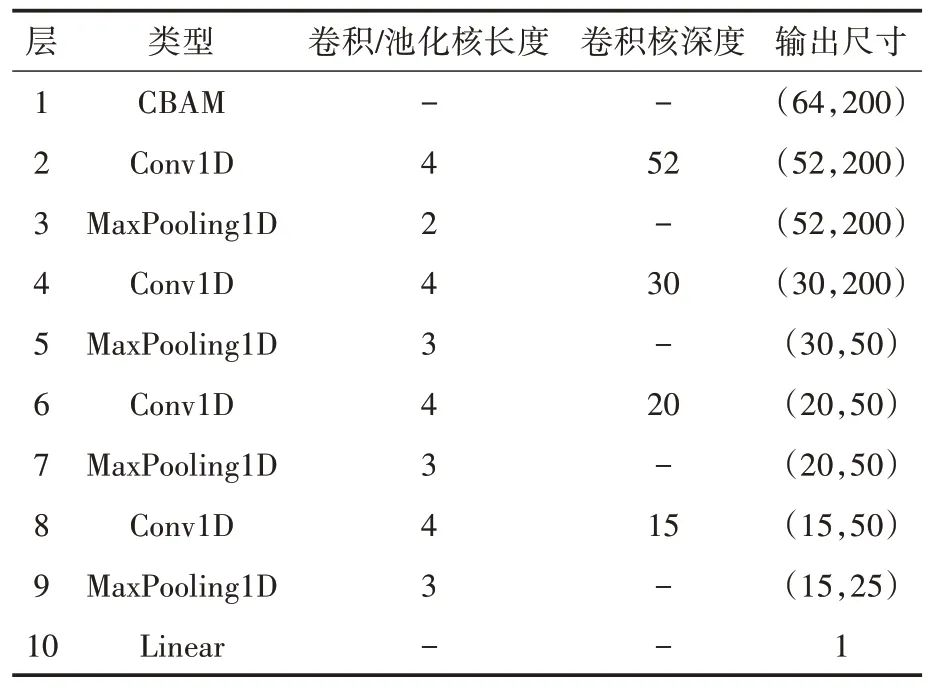
表1 CNN网络结构参数Tab.1 Parameters of CNN

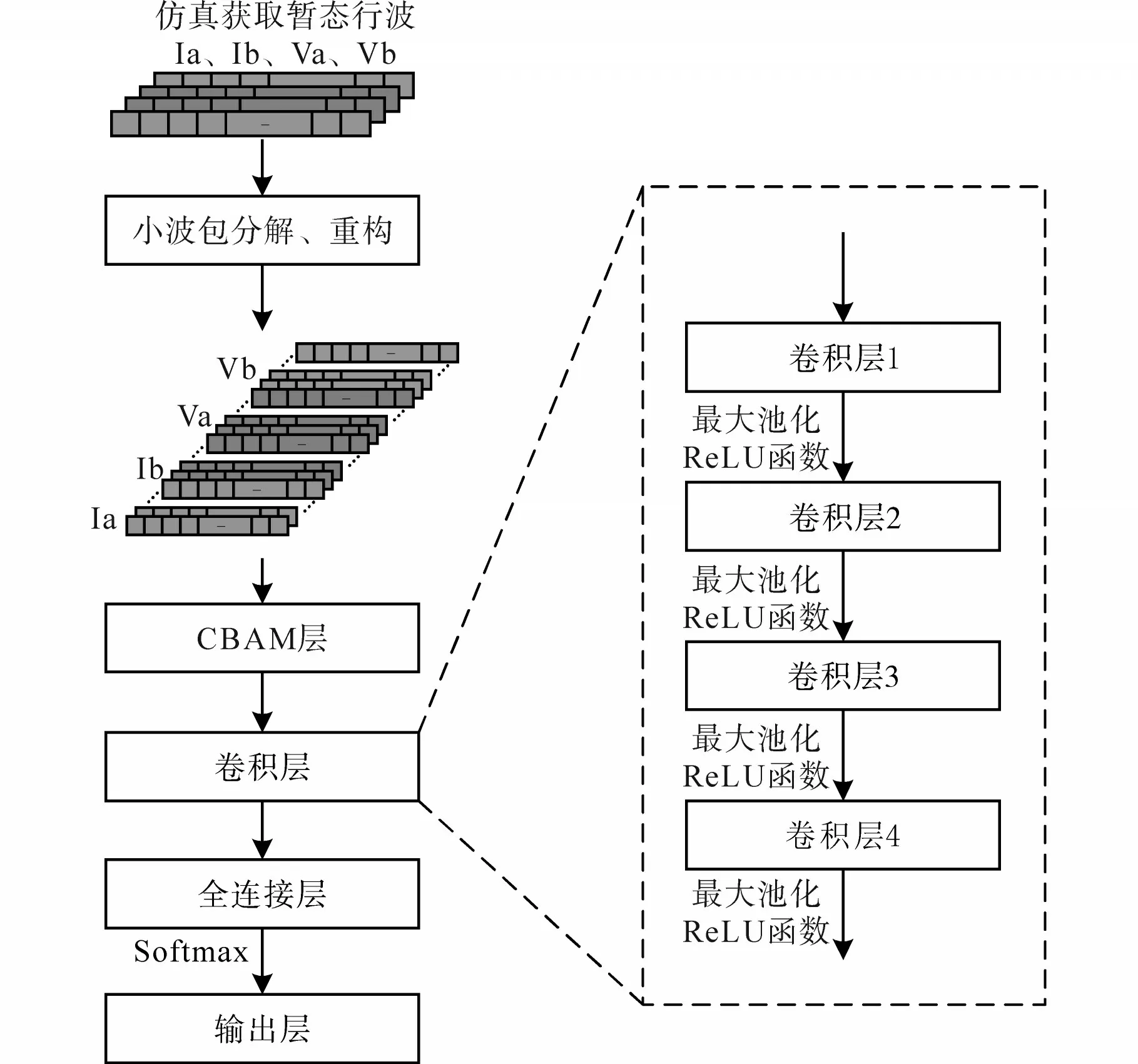
图4 基于时频分析的CBAM-CNN分类模型Fig.4 CBAM-CNN classification model based on JTFA

3 算例分析

3.1 直流系统仿真

为了扩充故障样本，使之更具备全面性和代表性，必须通过批量仿真获取真实可靠的多尺度故障样本。在南方电网超高压输电公司直流设备状态评估与故障诊断实验室的实时数字仿真平台（real time digital simulation system，RTDS）上对云广特高压直流输电系统模型的线路分别进行多次单极短路故障与雷击干扰仿真以采集故障暂态行波信号，云广特高压直流输电系统采用双极12脉动换流器，其拓扑结构如图5所示。

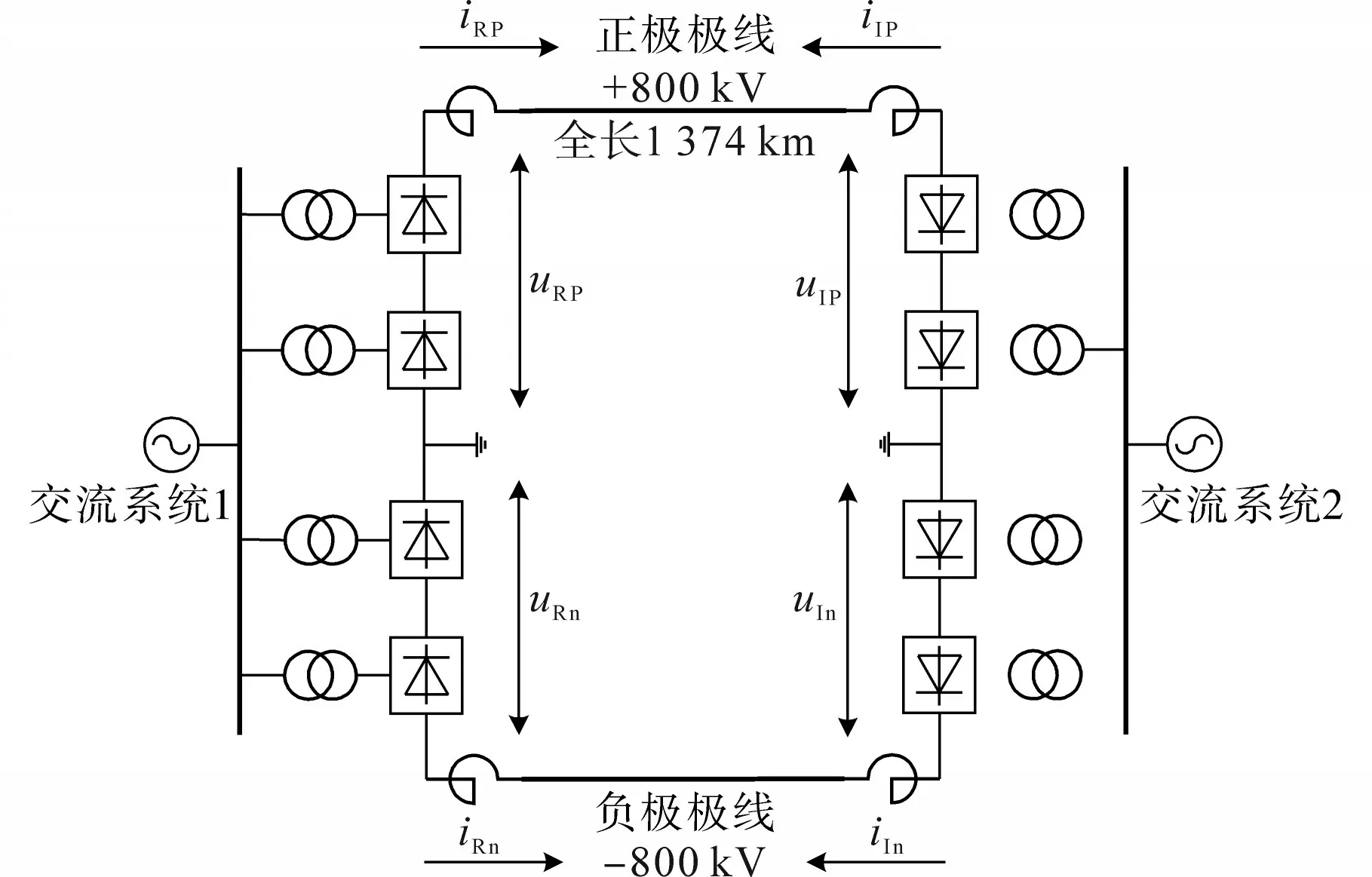
图5 云广特高压直流输电系统拓扑图Fig.5 Topology of Yunguang UHVDC transmission system

图5中iRp，iRn分别为整流侧正、负极电流；uRp，uRn分别为整流侧正、负极电压；iIp，iIn分别为逆变侧正、负极电流；uIp，uIn分别为逆变侧正、负极电压。仿真模型主要参数如表2所示。

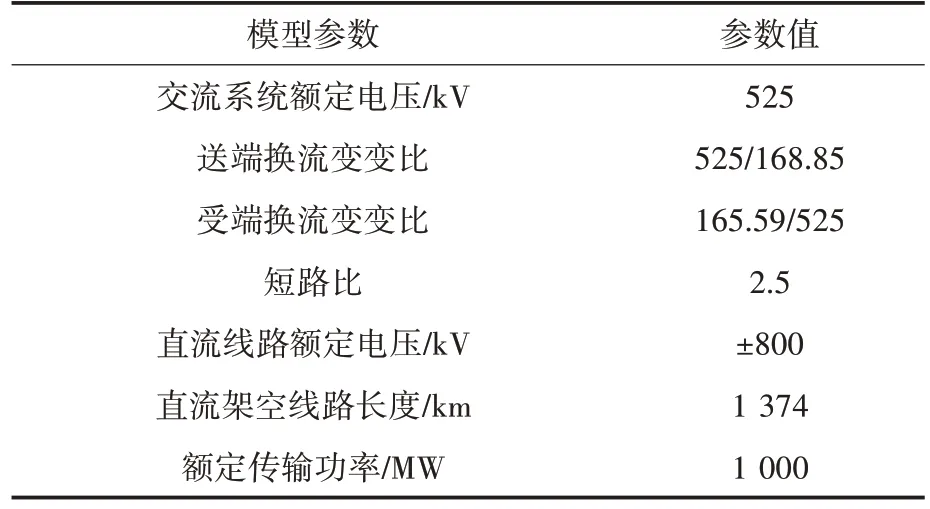
表2 云广特高压直流输电系统仿真模型参数Tab.2 Yunguang UHVDC transmission system simulation model parameters

为获取大量、全面的故障仿真样本并使样本具有代表性，在仿真模型线路上设置多种尺度的雷击和单极短路故障。雷电波为双指数函数，波形采用标准首次短时间雷击波形10/350 μs，考虑到雷击存在一定的随机性，对波形进行适度拉伸，将波头时间与半峰值时间的和定义为雷击持续时间。实际运行中短路故障的过渡电阻一般较小，故仿真样本中过渡电阻设置为不超过1 kΩ。批量仿真功能由RTDS 仿真平台的软件RSCAD图形化界面中提供的脚本功能实现，仿真步长50 μs，采样频率20 kHz，单极短路与雷击干扰的故障样本如表3和表4所示。

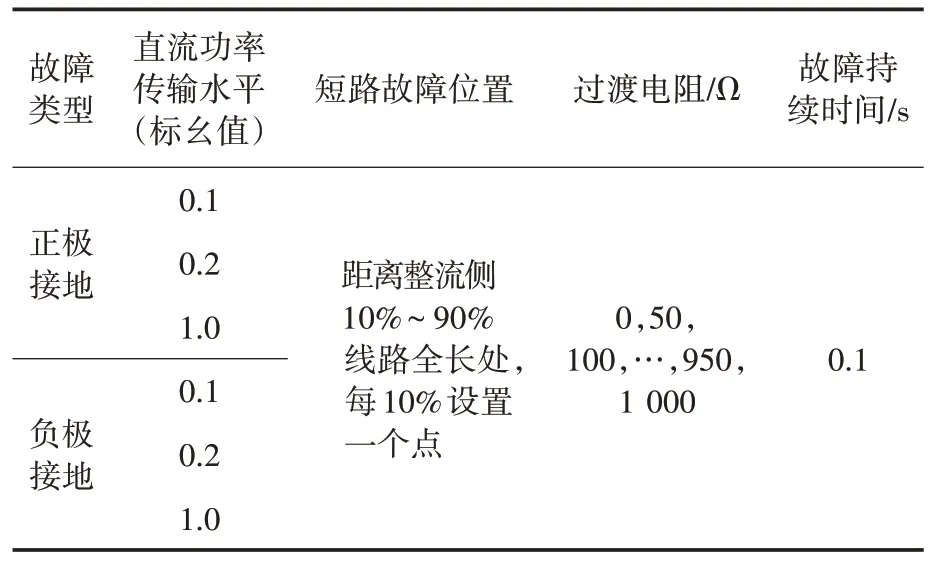
表3 单极短路故障样本集分布Tab.3 Unipolar short-circuit fault sample set distribution

表4 雷击干扰样本集分布Tab.4 Lightning interference sample set distribution

在第1 s 时设置短路故障或雷电绕击，剩余的时间用于进行波形采集以及系统恢复，每个故障样本包括线路两端换流站测量的正、负极的电流、电压共计8 个电气量波形，波形采样频率为20 kHz，波形采集的时间窗口为0.99 s—1.02 s，每个波形长达600个元素，并以故障尺度信息（故障类型、过渡电阻、故障点距离、故障持续时间、故障极）作为故障样本的标签向量。

由上述表格可知，通过仿真试验获取的单极短路故障样本共计2×3×10×21=1 260 个，雷击干扰样本共计6×3×3×2×10=1 080个。经数据清洗，剔除异常样本后最终用于故障分类模型学习的样本共计1 253+1 076=2 329 个，选用每侧电流、电压行波经相模解耦得到的1模分量组成样本。

以行波到达时刻前100个采样点与到达时刻后100个采样点组成故障样本。对全部样本的每一个波形信号均作4 层小波包分解，考虑到支撑长度与光滑性好的要求，选取db4作为小波基，每个波形共计24=16 个不同频带的分量，单个故障样本的大小为4×16×200个元素。

3.2 模型实用性验证

将样本集按照8∶2的比例随机划分为训练集与测试集，以故障类型标签作为CBAM-CNN 分类模型训练目标值，短路故障标记为0，雷击干扰标记为1。在Python3.8 环境下搭建本文所提CBAM-CNN 模型，模型基于PyTorch框架开发，计算机处理器型号为Intel（R）Core（TM）i5-6500 CPU@3.2GHz。设置CBAM-CNN模型迭代200次，使用同样的网络结构和超参数重复3 次试验，模型均收敛，训练过程平均用时147 s，测试集故障样本类型识别正确率均为100%，其中某次试验中CBAM-CNN模型训练结果如图6所示。

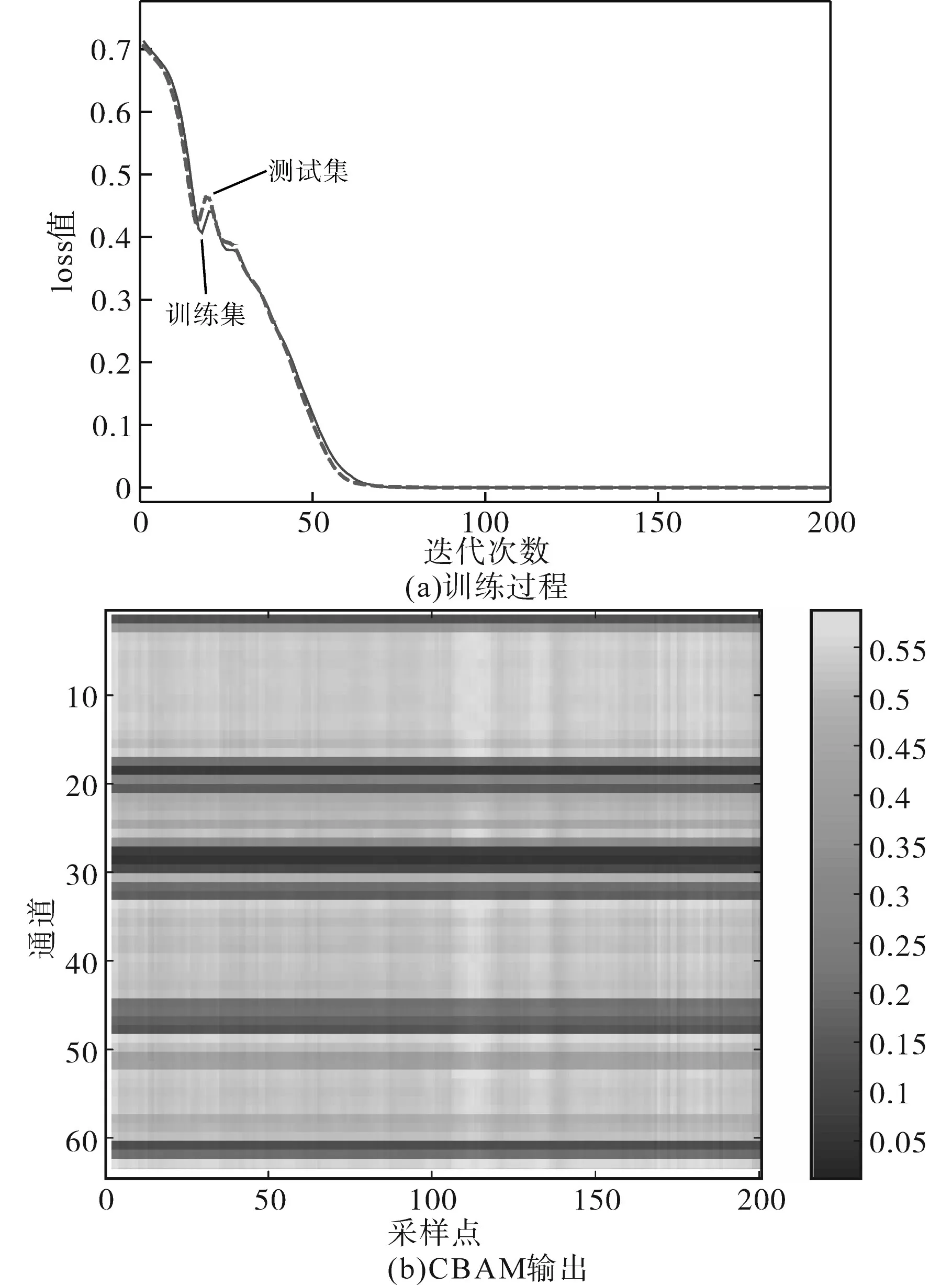
图6 CBAM-CNN模型训练结果Fig.6 Training results of CBAM-CNN model

图6a 为训练集和测试集loss 值的下降曲线，图6b为通道、空间两个维度的权重向量相乘后进行可视化得到的热图。由图6a可知，训练过程中训练集与测试集的误差同步收敛，且二者在下降至较小值后均保持平稳，测试集误差不再上升，表明模型能够实现对仿真数据集的正确拟合，不存在过拟合与欠拟合现象，训练得到的模型在该仿真数据集上适用性良好。由图6b可知，各个通道的权值相差相对较大，通道注意力机制明显降低了部分频带的权重；在波形全长范围内，空间注意力机制对波形第100～120 个采样点组成的片段赋予了最大的权值，该片段对应的是初始行波，由于没有经过多次折反射的干扰，初始行波表征的信息更接近于原始行波。可视化的结果证明空间注意力机制提取了有效的特征。

泛化能力是评估本文所提CNN-CBAM 模型实用性的直接指标。为了检验模型的泛化能力，需要避开接近于训练集的故障尺度参数，通过仿真设置更多故障以进一步扩充测试集，扩充部分的测试集雷击和故障点均位于正极，如表5所示。

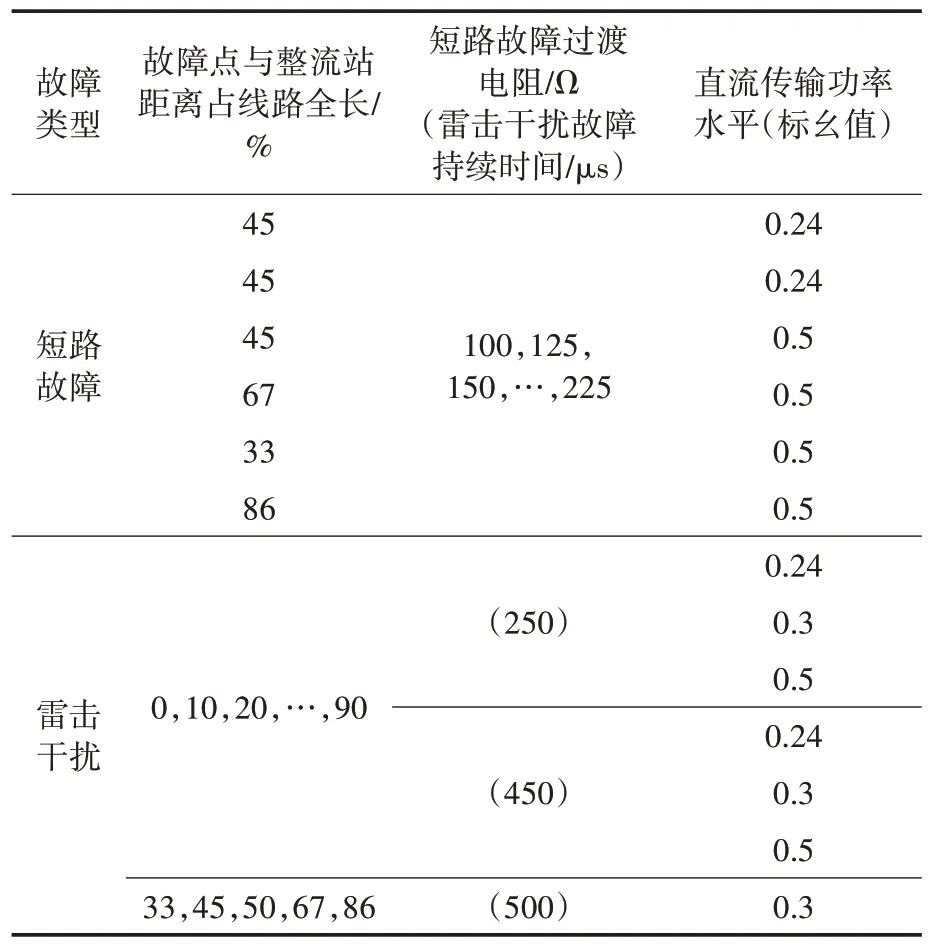
表5 扩充测试集样本分布Tab.5 Extended test set sample distribution

表5 中短路故障样本36 个，雷击干扰样本共计65 个。为了检验本文所提算法是否有效提升了识别准确率，将文献[4]的时域波形积分法、文献[8]基于行波高低频能量比值的识别方法、未经小波包分解的原始波形作为输入数据的CNN 模型和CBAM-CNN 模型、结合小波包分解的WPDCNN 模型作为对照组，深度学习模型分别训练3次，故障识别模型测试结果如表6所示。

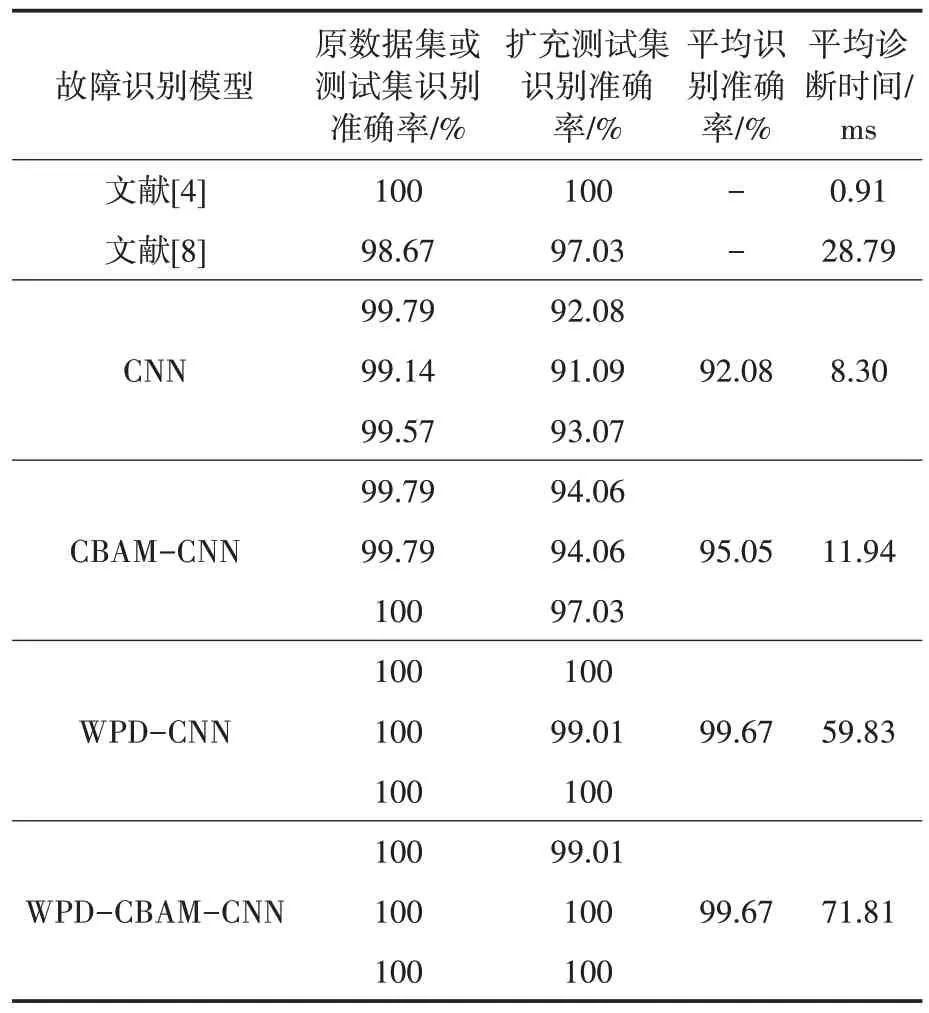
表6 不同故障识别模型的测试结果Tab.6 Test results of different fault identification models

由表6 可知，机器学习模型中WPD-CNN 模型、WPD-CBAM-CNN 模型诊断耗时更长，原因是需执行小波包分解以及分解后输入样本的通道增加，模型运算所需时间更长；加入了CBAM模块的模型需要推断注意力图和进行样本预处理，相比原始CNN 模型耗时略有增加。本文所提WPD-CBAM-CNN 模型耗时最长，但仍能在数十ms 内完成故障诊断，满足故障诊断快速性的要求，训练好的模型可用于实时识别。

在识别准确率上，深度学习算法对于原测试集的分类准确率均达到了99%以上，大部分试验中分类准确率达到100%，表明模型对于原数据集的适应性良好且训练过程不存在过拟合与欠拟合的错误。在扩充测试集上，采用了小波包分解的两个模型具有接近100%的识别准确率，与文献[4]的时域法接近，高于未进行小波包分解的两个CNN 模型，证明对输入样本进行时频分析预处理能为CNN 提供用于故障类型识别的有效特征，与文献[8]的频域法相比，识别准确率也有了一定的提升。

3.3 噪声鲁棒性验证

工程实际应用中，由于电磁干扰等多种因素，用于直流保护功能的信号不可避免地带有一定噪声，因此故障识别算法必须具备一定的抗噪能力。为了验证噪声干扰对本文算法的影响，在扩充测试集样本中每个电气量波形上加入信噪比（signal-to-noise ratio，SNR）分别为0 dB，5 dB，10 dB，20 dB 的高斯白噪声并应用于本文算法与对照组算法，每个模型分别训练3次并进行测试。加入不同SNR 的噪声后某个雷击干扰样本归一化后的电流行波1 模分量如图7 所示，测试结果如表7所示。

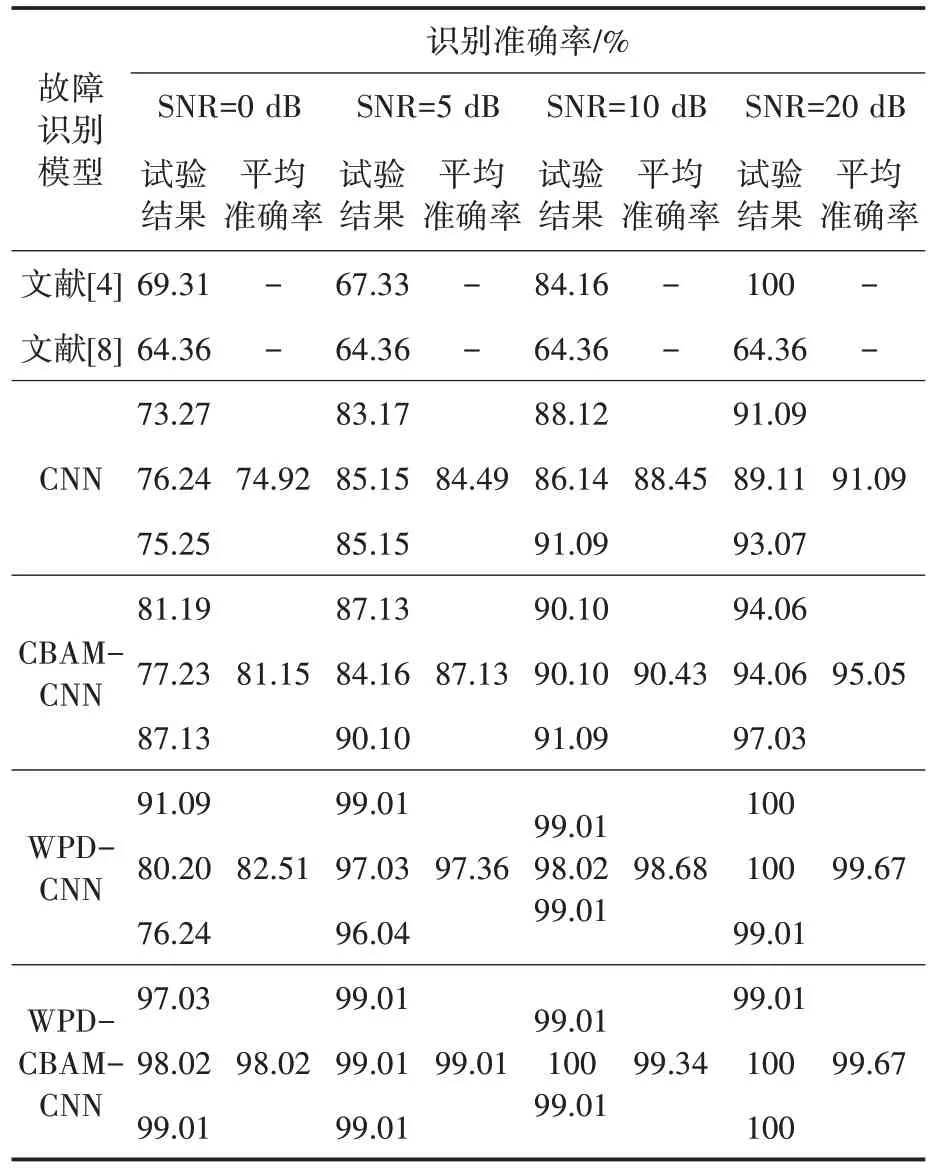
表7 不同故障识别模型的噪声鲁棒性测试结果Tab.7 Noise robustness test results of different fault identification models

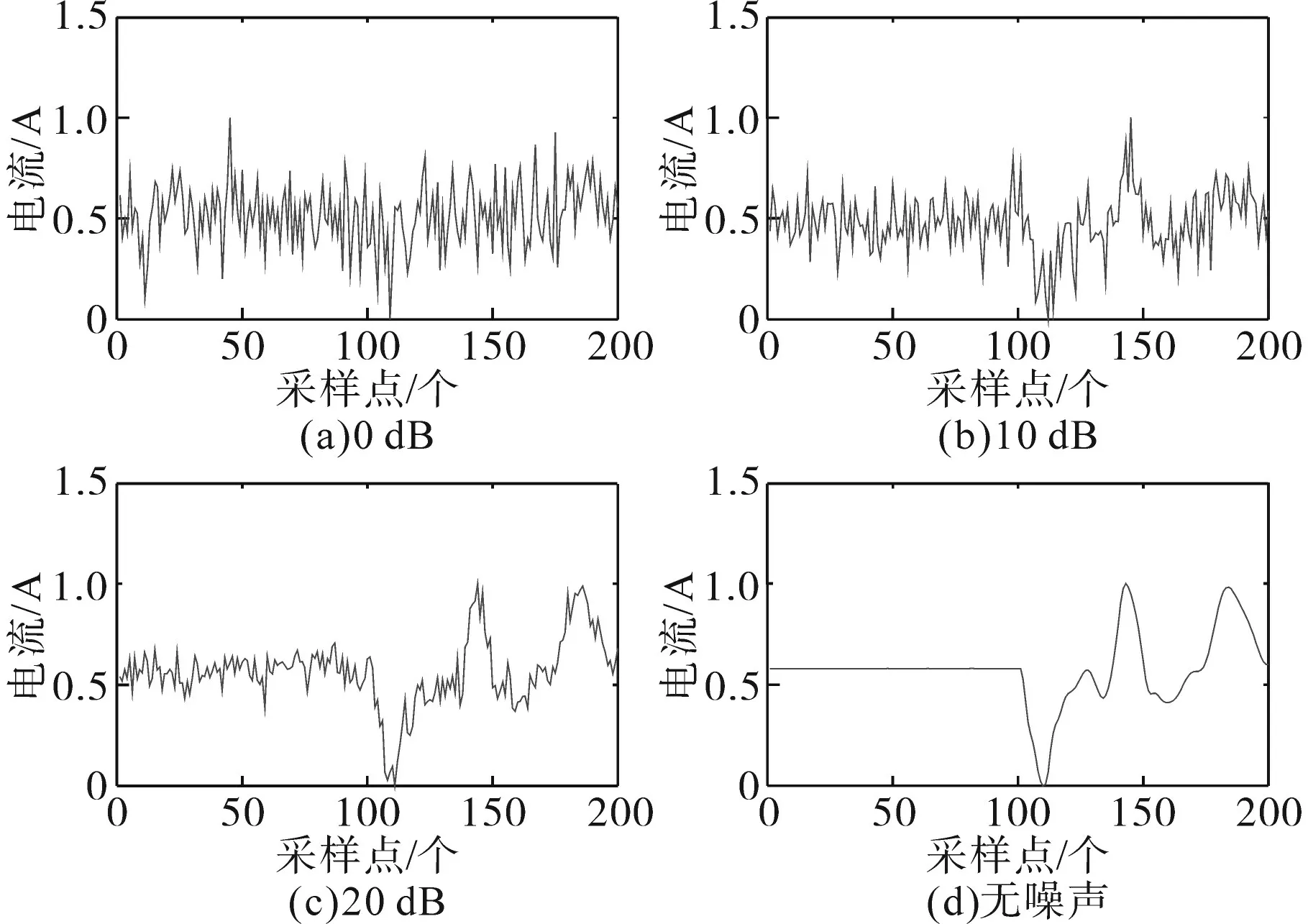
图7 加入不同强度噪声后的电流行波波形Fig.7 Current traveling wave waveforms after adding different intensity noise

由表7可知，随着噪声强度的增大，所有模型的识别准确率均有不同程度的下降。而加入CBAM 模块后识别准确率下降的幅度明显小于无CBAM 模块的模型，表明注意力机制提升了模型的抗噪能力。在噪声较小时，使用了WPD的模型识别准确率明显高于无WPD 的模型，但当SNR降低到0 dB时，WPD-CNN模型受噪声影响，其识别准确率已经不再具备优势，而本文所提WPDCBAM-CNN 模型仍然具有较高的识别准确率，拥有最佳的噪声鲁棒性。由图表可知，SNR 降低至10 dB 时噪声幅度较大，已难以识别电流行波波形的变化趋势特征，同时文献[4，8]的识别准确率降低至60%～70%。经进一步检验发现，噪声较大时文献[4，8]所构造特征的阈值均不再适用且特征区分度已不明显，从而导致判据失效，识别准确率急剧下降。综上所述，深度学习模型与传统算法相比噪声鲁棒性优势明显。

3.4 时频分析算法的影响验证

为了验证何种时频分析方法与CBAM-CNN模型结合具有最好的识别效果，分别选择应用较多的短时傅里叶变换、希尔伯特-黄变换与本文使用的小波包分解进行对比，3 次试验的识别结果如表8所示。

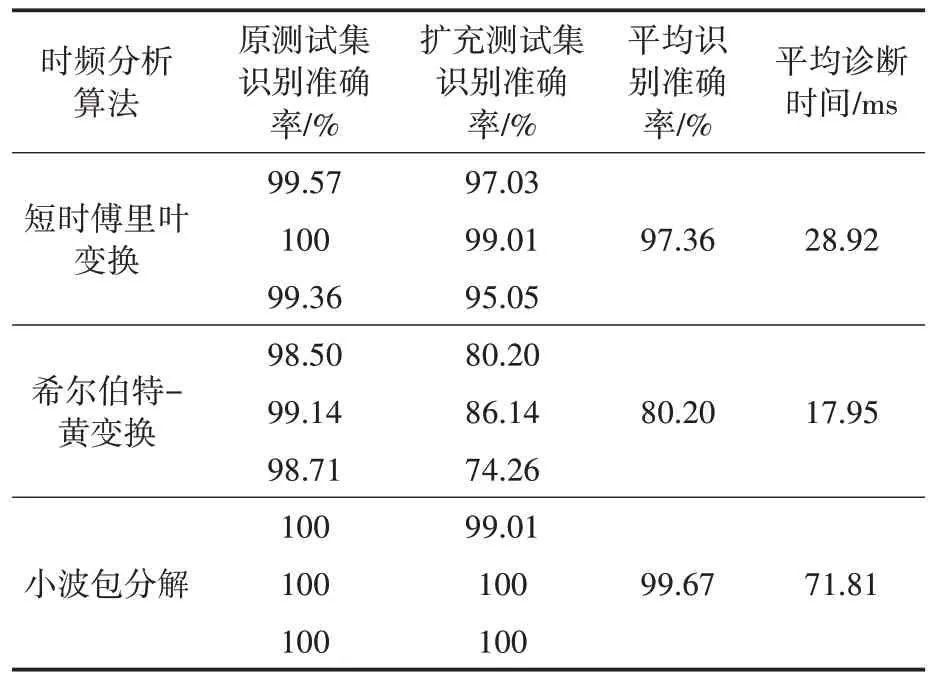
表8 不同时频分析算法的测试结果Tab.8 Test results of different JTFA algorithms

由表8 可知，时频分析算法的选取对识别效果的影响较大。希尔伯特-黄变换对于原数据集的识别准确率能达到98%以上，但对于扩充数据集的平均识别准确率仅能达到80.20%，泛化能力较差。短时傅里叶变换、小波包分解与CBAMCNN 模型的结合均能取得较好的识别效果。考虑到短时傅里叶变换窗口的长度固定，对于非平稳信号分析的效果存在局限性，实验结果证明了时频分析的质量对识别准确率存在影响，而小波包分析与CBAM-CNN 模型的结合能够取得最佳效果。

为进一步验证分解层数的选取对识别效果的影响，在同样的CNN网络参数配置下对比2，3，4，5 层分解在信噪比分别为0 dB，10 dB 与无噪声下3次试验的识别准确率，结果如表9所示。

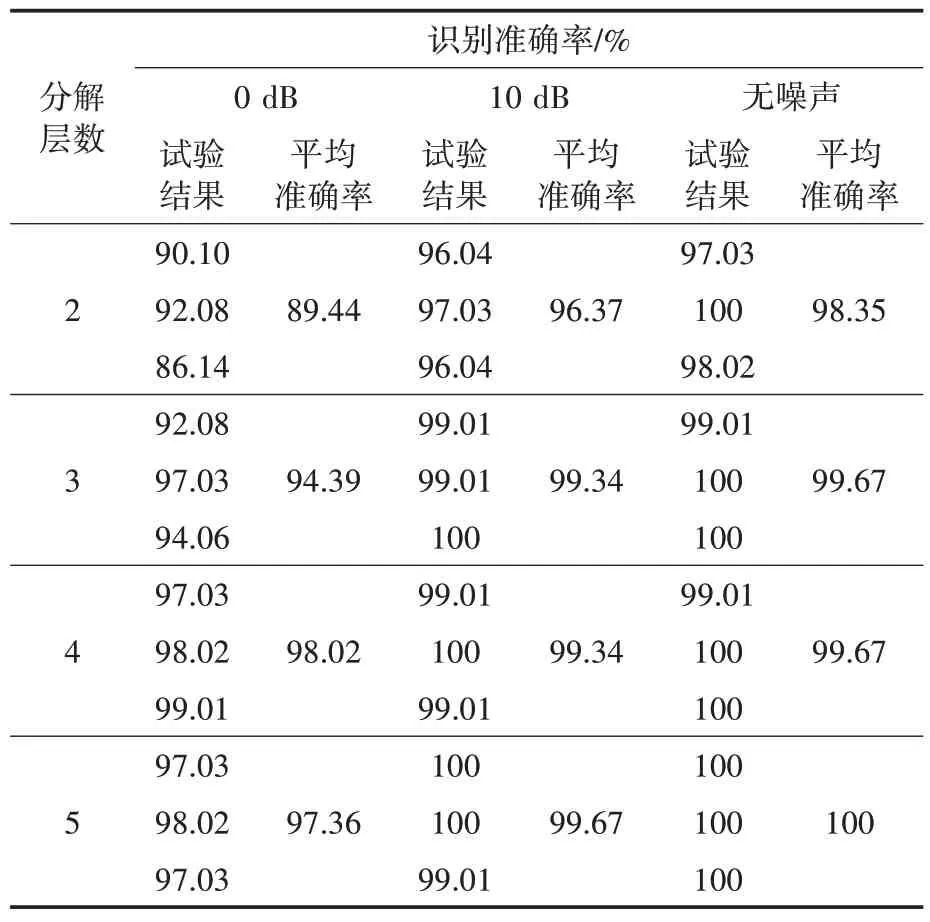
表9 不同小波包分解层数的测试结果Tab.9 Test results of different wavelet packet decomposition levels

由表9可知，在无噪以及噪声较小的情况下，3 层以上的小波包分解均能取得较好的识别效果。当SNR 降低至0 dB 时，4 层小波包分解效果最好，5层小波包分解的效果与之接近，但层数每增加1 时数据大小增加1 倍，计算消耗的硬件资源与时间也相应增加，因此分解层数设定为4 可取得最佳效果。

4 结论

针对故障识别研究存在提取特征复杂、有限的判据难以全面刻画、有效区分雷击干扰与短路故障的问题，提出了结合基于小波包分解的行波时频分析，构建CBAM-CNN 网络自动学习故障特征并实现分类的方法，并通过仿真分析验证了模型的实用性、噪声鲁棒性以及时频分析算法和小波包分解参数的影响，得到结论如下：

1）对输入样本进行时频分析处理能够有效地提升模型的泛化能力，WPD-CNN 与WPDCBAM-CNN 模型的识别准确率较高，加入CBAM模块后识别效果略有上升。

2）所提模型相比对照组抗噪能力优秀，对于信噪比低至0 dB 的行波波形仍具有良好的识别能力，CBAM模块明显提升了噪声鲁棒性。

3）时频分析算法的选取对于模型识别效果具有重要影响，小波包分解与CBAM-CNN 模型结合后表现出的性能优于短时傅里叶变换与希尔伯特-黄变换，小波包分解层数取4时具有最佳的性能。