基于支持向量机参数优化的高温合金表面缺陷磁异常定量研究

胡 博 罗炜韬 王少飞 蓝希旺

南昌航空大学无损检测技术教育部重点实验室,南昌,330063

0 引言

高温合金是航空发动机涡轮盘的主要材料。低循环疲劳失效是涡轮盘的主要失效模式,极易产生疲劳裂纹缺陷。对于涡轮盘的无损检测技术,其中较为成熟的方法是超声波法,但超声波检测受声波与裂纹夹角的影响,易漏检裂纹、非轴向夹杂等较小尺寸缺陷。弱磁、涡流等电磁检测新技术也有相关的应用,但对缺陷的定量评价还存在不足。弱磁检测技术在天然地磁场环境下进行检测[1],无需外加激励,操作方便,非常适用于涡轮盘表面缺陷的快速检测[2]。基于此,研究高温合金表面缺陷的弱磁检测信号定量算法对解决实际检测的工程问题具有重要意义。

电磁无损检测缺陷反演定量方面,漏磁和涡流检测的研究较为成熟。LIU等[3]对NdFe35材料的漏磁信号进行仿真分析,建立了缺陷尺寸和漏磁特征的关系,为铁磁性材料的缺陷量化提供了一定参考。杨涛等[4]基于漏磁检测,针对管道缺陷进行定量研究,提出一种人机交互式的方法,提高了缺陷信号分析效率和定量精度。SHI等[5]应用基于温度变化导数的脉冲涡流检测法对45钢裂纹尺寸进行定量研究,发现裂纹长度和宽度的定量误差均小于1%。KUTS等[6]通过分析谐波和脉冲激励下涡流信号幅值的变化来估计检测对象表面裂纹缺陷的深度。RAMUHALLI等[7]、JOSHI等[8]通过训练神经网络中的基函数,得到了电磁检测信号对缺陷特征的空间映射,实现了缺陷的定量化表征。ZHANG等[9]提出了一种新型基于两组神经网络的钢丝绳内部和表面缺陷的定量检测方法,所提方法不仅可以区分内部和表面缺陷,还可以定量检测宽度、横截面损失率和位置深度。KHODAYARI-ROSTAMABAD等[10]在漏磁检测中采用深度学习技术,对管壁缺陷、异常现象进行检测并对缺陷严重程度进行了评估。JUN等[11]通过建立单一变化尺寸与检测信号特征值的关系,实现了缺陷定量,但当缺陷多个尺寸同时发生变化时,该映射关系不再适用。PRIEWALD等[12]基于有限元分析的漏磁场非线性正演模型推导二维反演重构问题,采用高斯-牛顿优化算法重建钢板缺陷的几何尺寸。FU等[13]针对304奥氏体不锈钢材料,利用支持向量机算法对样本库内的缺陷进行定量研究,其中长度定量精度为92.91%,宽度定量精度为80.70%,但缺陷深度的定量精度仅为65.63%,其深度精度还有待提高。

结合已有的研究成果[2,13],应用弱磁检测技术,本文提出一种基于支持向量机(support vector machine,SVM)参数优化的高温合金表面缺陷磁异常定量方法,训练SVM模型,建立磁异常信号特征值与缺陷参数之间函数关系的近似表达式,采用交叉验证法和遗传算法进行参数优化后比较反演结果,验证了所提方法可提高高温合金表面缺陷反演定量精度。

1 实验方法

1.1 弱磁检测

弱磁检测技术是在天然地磁场环境下,通过高精度磁传感器在高温合金试件表面按一定路径进行扫查,采集垂直于试件表面方向上磁感应强度的变化数据。该技术的检测原理示意图见图1。查阅相关资料可知镍基高温合金的相对磁导率介于1.023 72～1.026 23之间[2],当缺陷位于试件表面时,缺陷内空气介质的相对磁导率小于试件本体的相对磁导率(即μ′<μ),缺陷会排斥磁力线,试件表面的磁感应强度将减小,采集到的磁感应强度曲线会表现出向下凸起的磁异常;若缺陷内夹杂了铁磁性介质,则其相对磁导率远大于试件本体的相对磁导率(即μ′>μ),缺陷会吸引磁力线,试件表面的磁感应强度将增大,采集到的磁感应强度曲线会表现出向上凸起的磁异常。

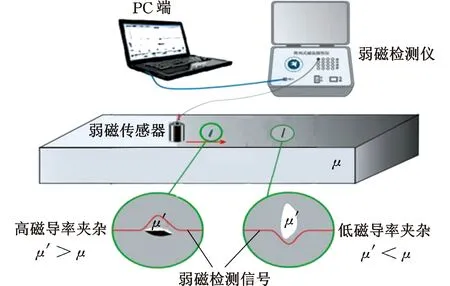
图1 弱磁检测原理示意图

采用GH4169高温合金材料加工4个试件,编号为1～4,试件的尺寸均为 300 mm×100 mm×5 mm(长×宽×高)。在试件表面中心处等间隔位置加工矩形槽来模拟表面缺陷,在每个试件上制作4个矩形槽,矩形槽长度分别为10,13,16,20 mm,宽度分别为0.30,0.35,0.40,0.45 mm,深度分别为1,2,3,4 mm,共16个缺陷,编号为1～16。使用分辨率为1 nT的磁通门传感器进行检测,传感器量程为±250 μT。将传感器放置于试件左端中心位置,从左向右沿表面匀速扫查,扫查长度为300 mm。试件和检测示意图见图2。将得到的16个缺陷弱磁信号异常数据作为样本库训练SVM模型。同时,为验证参数优化后缺陷反演模型的准确性,对文献[2]中的高温合金试件进行弱磁检测和定量评价,将其称之为验证件。验证件两个表面(A面和B面)分别预置了3个不同规格的槽型缺陷,如图3所示。

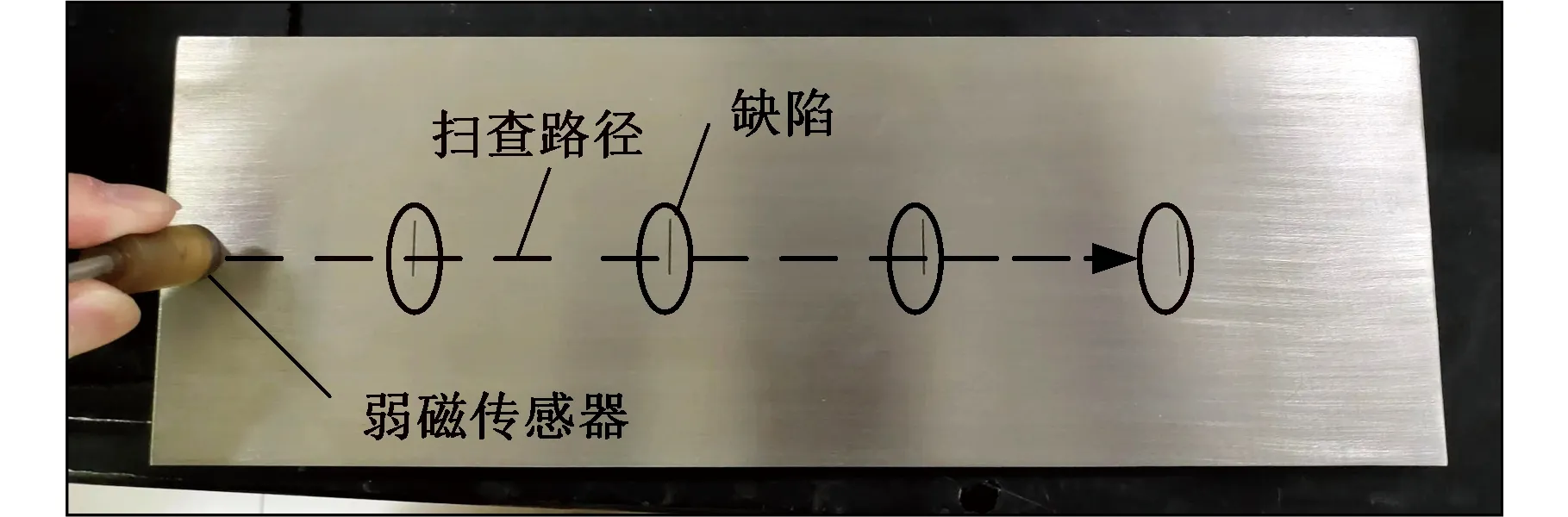
图2 样本库试件和弱磁检测示意图

图3 验证件结构示意图

1.2 SVM算法

SVM算法是为了解决非线性回归和分类问题而提出的一种建立在机器学习上的结构风险最小化算法理论[14]。通过已知的一个小样本库构建训练集和测试集,该样本库由弱磁检测得到的16个缺陷磁异常数据的特征值构成。训练集用于训练预测模型,测试集用于模型准确度的测试,进而将实际检测的弱磁信号特征值代入预测模型中预测缺陷尺寸参数,实现缺陷的反演定量。其中,训练集如下:

T={(x1,y1),(x2,y2),…,(xi,yi),…,(xN,yN)}

(1)

式中,i=1,2,…,N,N为样本总数;xi为第i个特征量,xi∈Rn(Rn为n维实数集);yi为xi对应的标签,yi∈{-1,1)};(xi,yi)为训练集T中的第i个样本。

SVM的核心思想是将输入向量(即样本库数据)通过某种预先选择好的非线性映射转换到一个高维度特征空间[15],将非线性回归和分类问题转化为线性问题的求解,进而在这个特征空间中构造一个最优分类超平面。在所有训练集样本能被划分的前提下,若某个超平面能够将训练集准确地分开,并且离超平面最近的向量与超平面之间的距离最大,则此超平面被称为最优超平面。线性可分SVM学习得到的分离超平面为

wTx+b=0

(2)

x=(x1,x2,…,xi,…,xN)

式中,ω为超平面的法向量,决定超平面的方向;b为偏置量,即超平面相对原点的偏移。

得到的分类决策函数为

f(x)=sign(wTx+b)

(3)

线性情况下寻找最优超平面是一个凸二次规划问题,其求解仅涉及到向量的内积运算,因此,为了在特征空间中构造超平面,并不需要以显式的形式来考虑特征空间,只需要知道这个空间中的内积运算。SVM通过引入核函数来实现高维特征空间中的内积运算。核函数可将原空间中的非线性问题通过内积运算变换为特征空间中的线性问题。当解决非线性映射问题时,一般采用径向基核函数。

1.3 参数优化

使用径向基核函数的SVM算法有两个重要参数C和g,其中C为惩罚系数(即对预测结果偏差的容忍度[16]),C过大或过小时,对训练集样本以外的预测效果都会变差;g为径向基核函数的宽度参数,g的大小与支持向量的个数成反比,而支持向量的个数影响训练与预测的速度。由此,为了提高缺陷反演定量结果的准确度和反演速度,有必要对C和g进行优化,得到合适的模型参数。

参数优化方法有交叉验证法[17]、粒子群优化算法和遗传算法[18]等,其中交叉验证法应用最广,收敛速度较快,但容易陷入局部最优,要求目标函数对参数可微。遗传算法和粒子群优化算法不要求目标函数的可微性,基本上是全局收敛的,已有研究验证了这些算法用于SVM参数调整的有效性[19]。全局方法的主要缺点是计算时间过长,且通常产生的是近似最优解。为了获得较好的模型参数,分别采用交叉验证法和遗传算法进行参数优化,使用MATLAB软件编程实现,选取效果较好的一组参数作为最优解。两种方法的实现流程如图4所示。

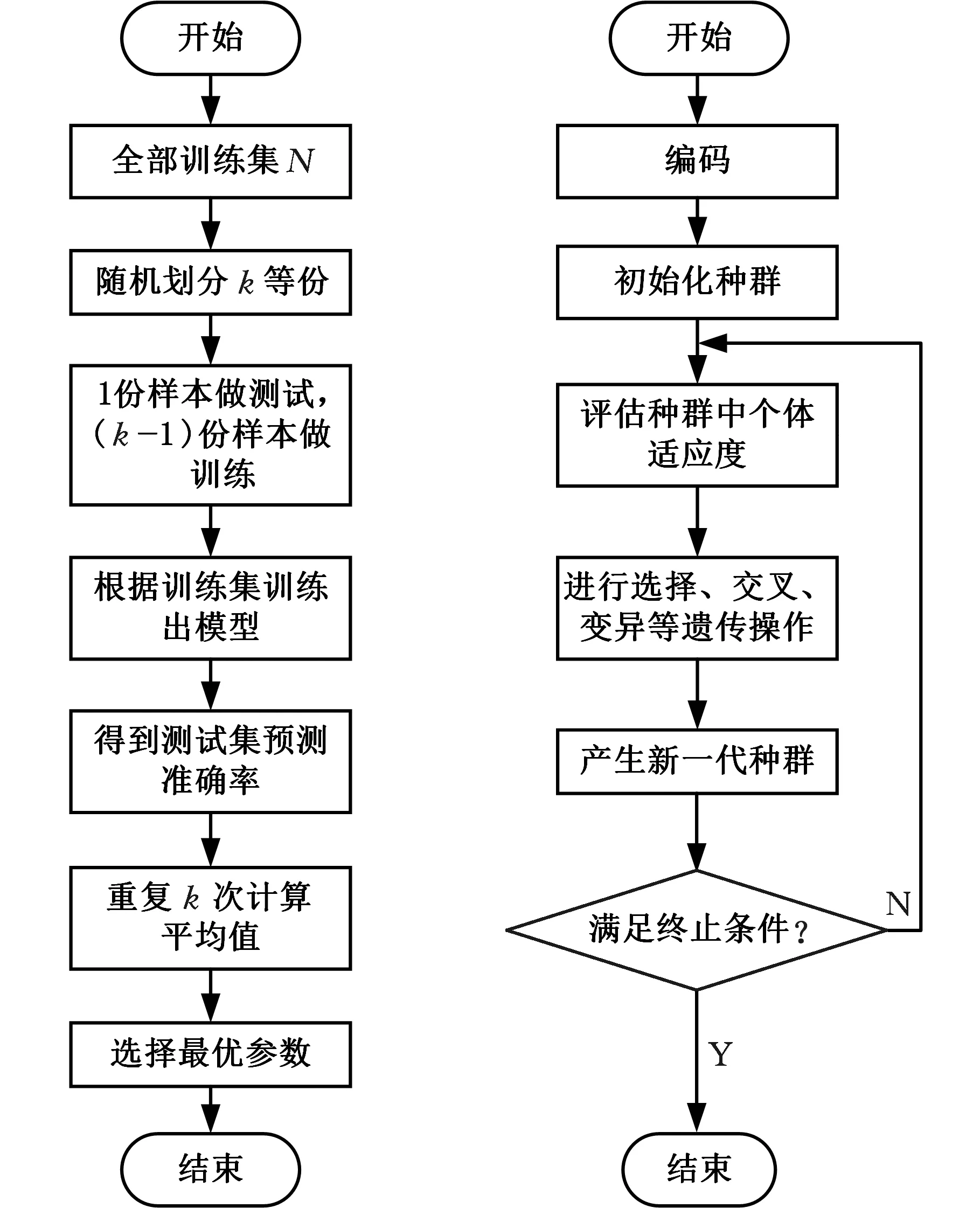
(a)交叉验证法流程图 (b)遗传算法流程图

根据SVM模型输出变量的性质,将研究问题分为回归问题和分类问题。当输出变量为定量变量时,为回归问题;当输出变量为定性变量时,为分类问题。高温合金表面缺陷的定量化反演问题本质是一种定量问题,也就是回归问题。在回归问题中,一般使用均方误差(MSE)表示模型准确度的测试误差,可表示为

(4)

式中,zi为第i个样本的真实值;pi为模型给出的第i个样本的预测值。

交叉验证法中,k折交叉验证的平均均方误差可表示为

(5)

其中,VMSE,m为第m次交叉验证时的均方误差。平均均方误差数值越小,则交叉验证法对应的模型参数更优。

遗传算法中,个体的好坏用适应度来评价,在缺陷反演定量问题中,适应度数值越大,解的质量越高,反演的结果就越准确。用均方误差来表征适应度函数,可令均方误差的最小值对应适应度的最大值,因此求解最佳适应度即为求函数表达式(4)的最大值。适应度取最佳值时,则遗传算法对应的模型参数最优。

1.4 特征值提取和反演流程

根据弱磁检测原理可知,高温合金表面缺陷在垂直于试件表面方向磁感应强度曲线上表现出向上或向下凸起的磁异常特征[2]。缺陷磁异常数据的特征值包括形态特征、时域特征和频域特征,由文献[12]可知,在弱磁检测定量研究中提取形态特征可以减少大量的数据处理工作,且与提取所有的特征进行反演的结果并无明显区别,因此本文采用形态特征作为弱磁信号特征量进行定量研究。形态特征包括占宽、幅值和面积,如图5所示。磁异常为向上的凸起时,将曲线从平稳至突然攀升阶段的转折点与下滑至平稳阶段的转折点之间的横坐标之差的一半作为磁异常特征的占宽;将转折点与顶点之间的纵坐标之差作为磁异常特征的幅值;将磁异常信号曲线的半波面积作为磁异常特征的面积。磁异常为向下的凸起时,采取相同的方法提取特征值。将1～4号试件的16组缺陷特征值数据作为样本库,其中15组作为训练集,1组作为测试集,建立样本库与缺陷参数之间的映射关系。

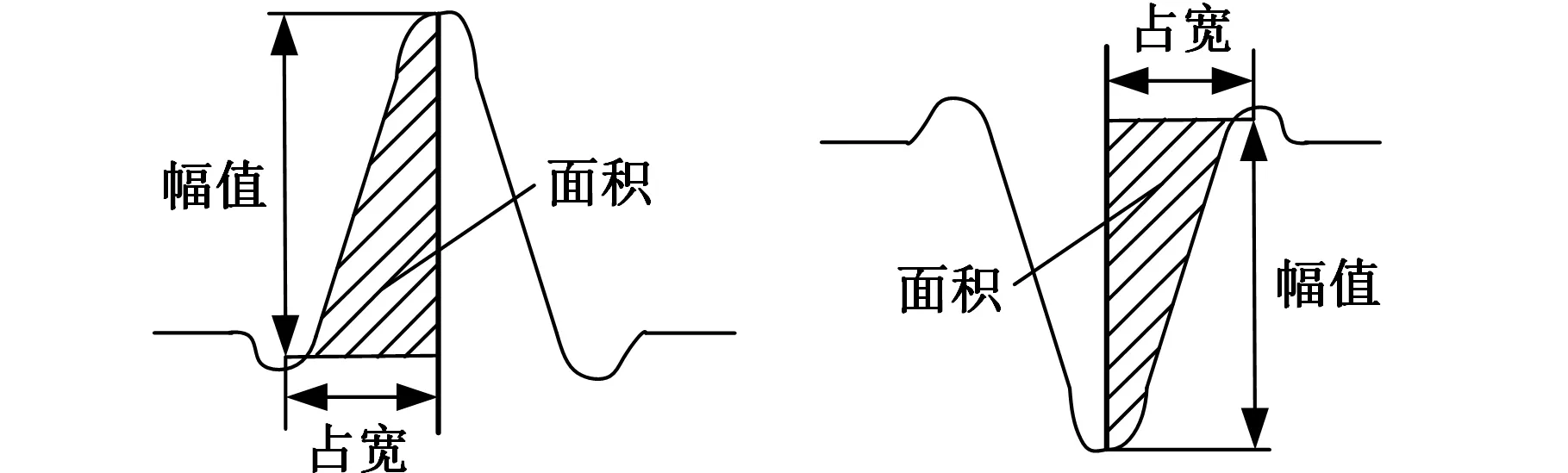
图5 特征值提取示意图

分别对裂纹缺陷的长度、宽度和深度构造预测模型进行训练,缺陷的反演流程如图6所示。

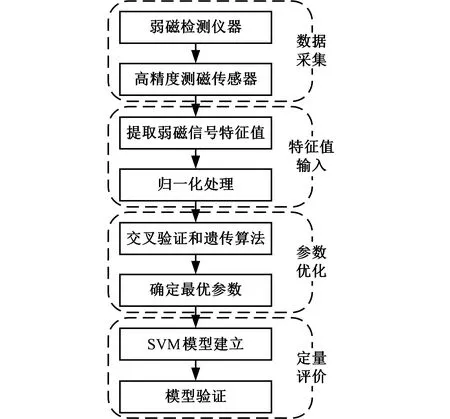
图6 缺陷反演流程图

具体的反演程序通过MATLAB中LIBSVM工具箱来进行,该工具箱中SVM算法参数C和g是默认值,按照交叉验证法和遗传算法寻优得到的优化参数,对默认参数进行修改,再训练得到优化后的模型。

2 结果和讨论

2.1 弱磁检测结果

经测磁传感器在1～4号试件表面扫查后,得到4个试件中心位置扫查路径上垂直于试件表面的磁感应强度曲线,见图7。4条曲线在缺陷位置均产生向下凸起的磁异常,由于缺陷尺寸不一致,故所产生的磁异常形态和数值各不相同。提取16个缺陷的磁异常特征值,具体见表1,其中面积参数值是指对检测信号曲线的半波波形进行积分得到的数据值,为量纲一常数,表中数据可用于后续SVM模型算法的构建。

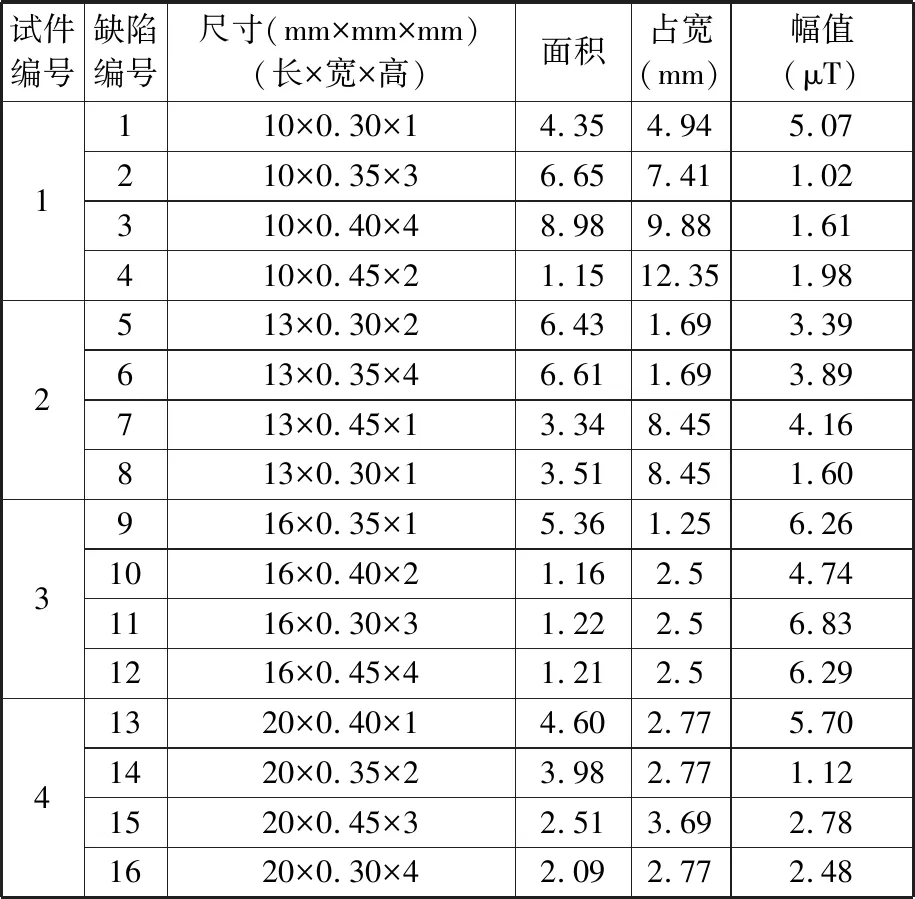
表1 弱磁信号特征值

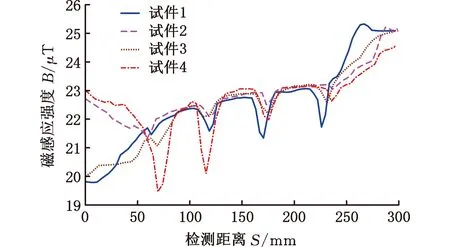
图7 弱磁检测信号图

2.2 参数优化后的反演结果

采用交叉验证法和遗传算法对SVM算法进行参数优化,参数C和g的范围均设置为0.01～100,迭代步长均为0.5。考虑到样本数目的有限性,选择3折交叉验证法进行参数寻优,以深度模型为例,寻优过程中均方误差如图8所示,其中横坐标为参数C和g的搜索范围,纵坐标为均方误差,描述了交叉验证法在一定范围内搜索最佳参数使得均方误差最小的过程。遗传算法种群数量设为20,进化代数设为100,以深度模型为例,图9给出了适应度的变化曲线,描述了遗传算法在一定范围内搜索得到最优参数使得种群达到最佳适应度的过程,当种群进化代数接近100时,此时已达到最佳适应度值。优化后参数C和g的结果见表2。

表2 参数优化结果与预测准确度

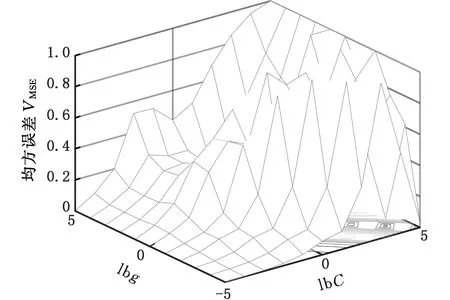
图8 交叉验证法均方误差图

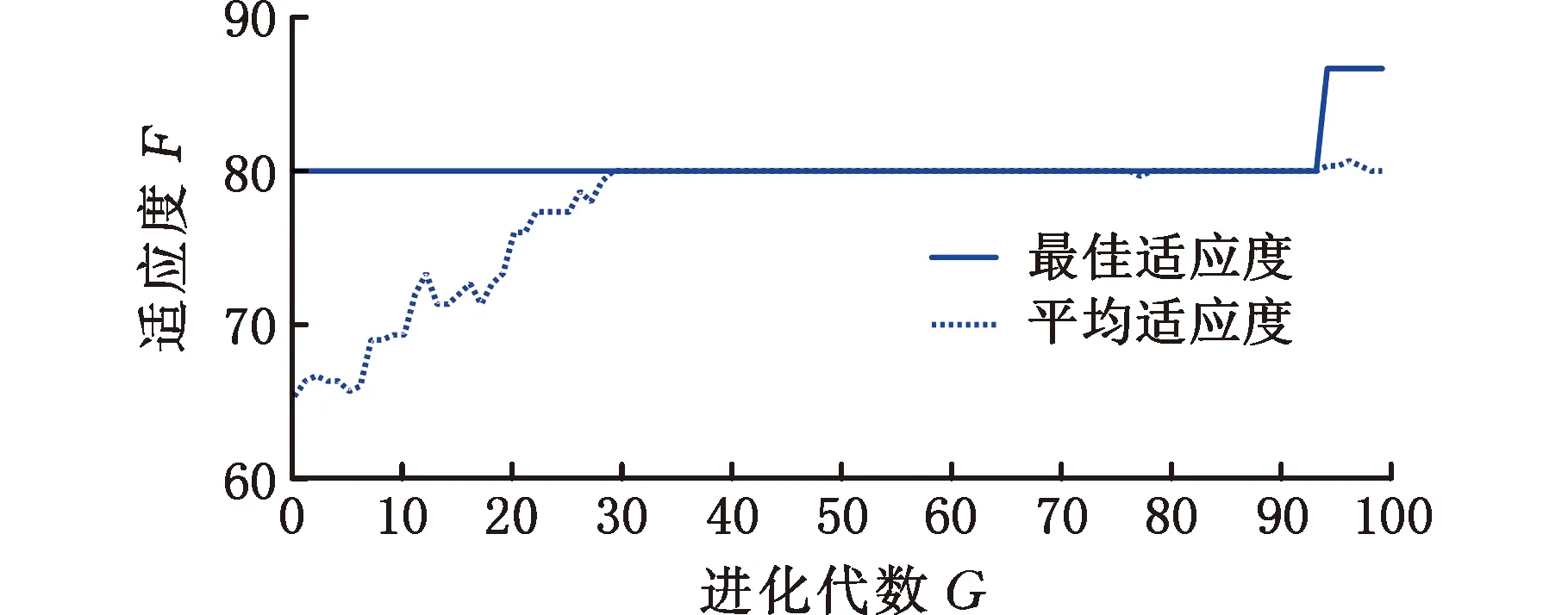
图9 遗传算法适应度曲线

将16组特征值数据划分成16种训练集和测试集的组合,构建SVM算法得到长度、宽度、深度3个模型的预测缺陷尺寸,LIBSVM默认参数和优化后参数的预测结果与实际缺陷尺寸的16组预测准确度的平均值见表2,由于采用的核函数参数不同,导致长度、宽度和深度模型反演结果之间存在差异。但经参数优化后,长度、宽度、深度的预测结果比默认参数的预测结果都有提高,尤其是长度和深度的反演效果有显著提高;遗传算法比交叉验证法的预测准确度更高,长度、宽度、深度分别达到了95.87%、91.92%和78.56%,因此选用遗传算法优化后的参数为最佳参数来建立缺陷反演模型。

2.3 模型验证

在相同的实验条件下,对验证件进行弱磁检测和磁异常特征值提取。为了验证检测结果的重复性,试件A面连续检测两次,图10[2]所示为试件A面的两次检测结果,图11[2]所示为试件B面的检测结果。该试件A面上的3个缺陷从左到右编号为1～3,B面上的3个缺陷从左到右编号为4～6,其中第6个缺陷中参杂了少量铁粉,用于模拟铁磁性夹杂,这导致检测信号在缺陷处产生向上凸起的磁异常,而其余的缺陷信号凸起均为向下。由于铁磁性夹杂与母材的磁导率差异远大于空气与母材的磁导率差异,因此第6个缺陷产生的磁异常特征幅值偏大,对预测结果会产生偏差。为了减小这种偏差,本文对该缺陷信号特征值幅值和面积缩小1/2后进行反演。经数据提取后,缺陷特征值见表3,表中第6号缺陷的特征值是由原始检测数据提取的特征值,第7号缺陷的特征值是第6号缺陷的面积和幅值减半后的特征值,占宽保持不变。将提取的特征值代入遗传算法优化参数后的SVM反演模型中,得到7组数据长、宽、深的预测尺寸如图12所示,对应预测准确度见表3。

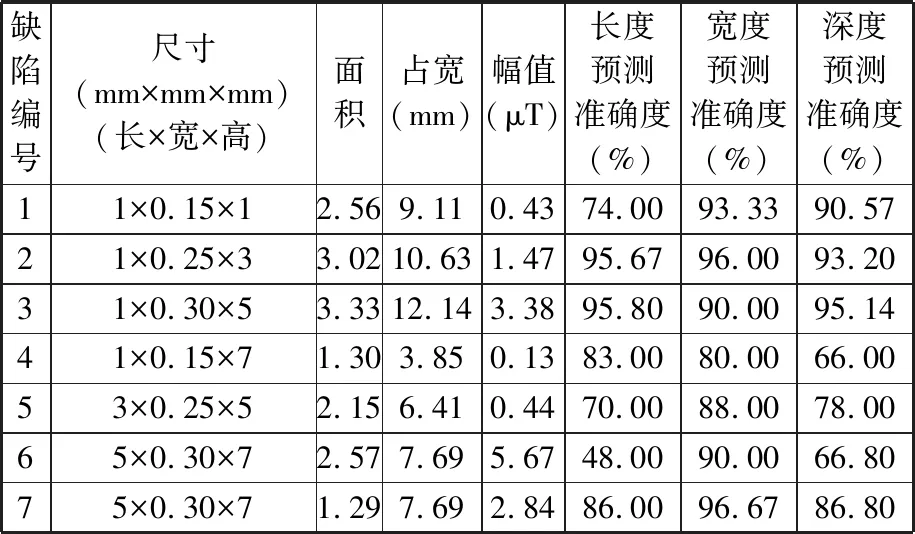
表3 高温合金缺陷特征值和预测准确度

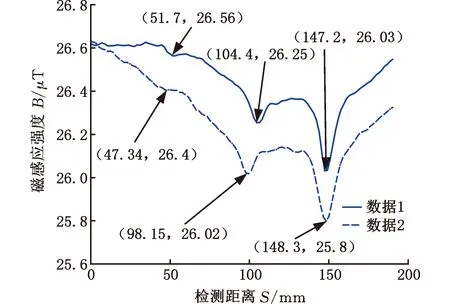
图10 试件A面两次检测结果图

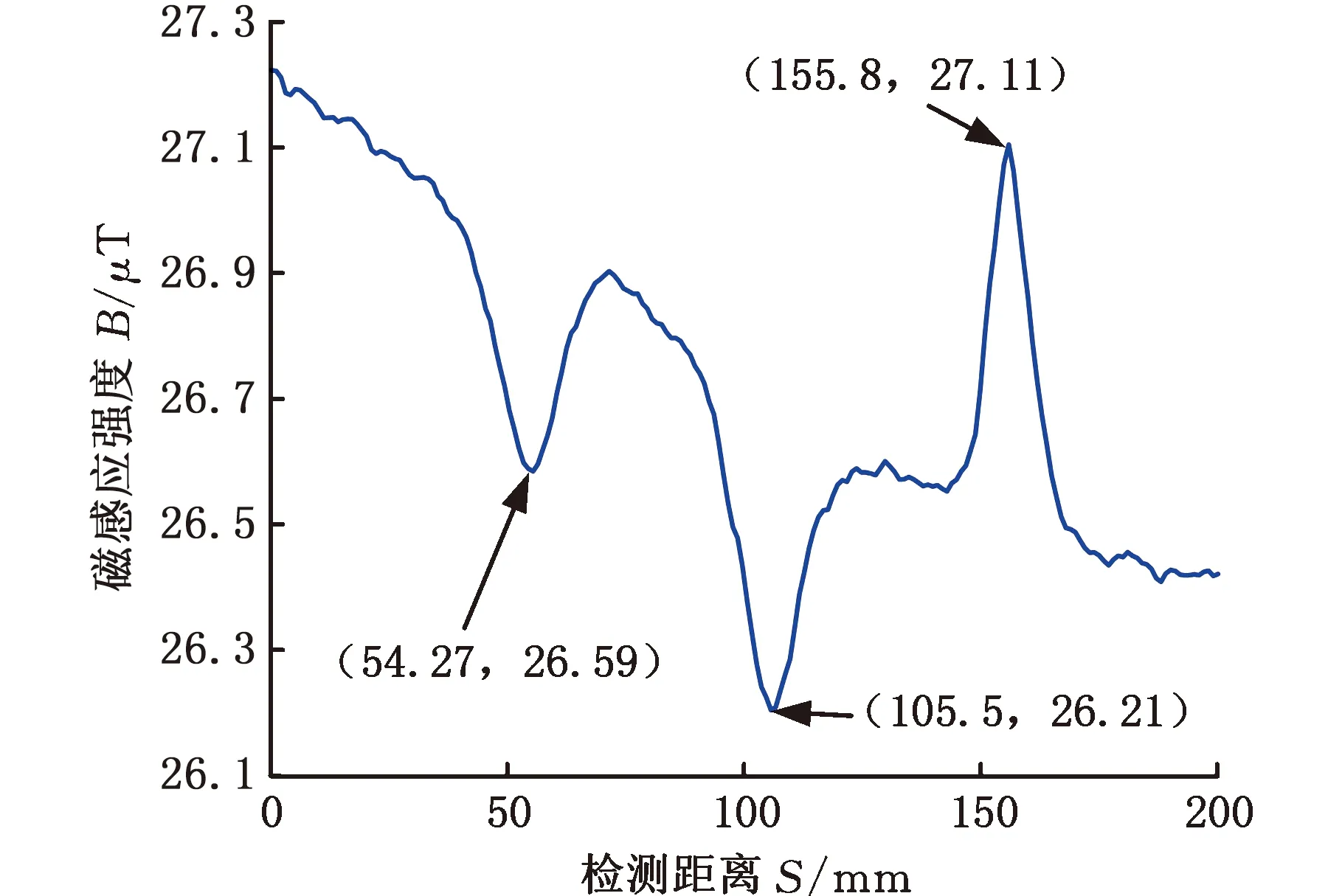
图11 试件B面检测结果

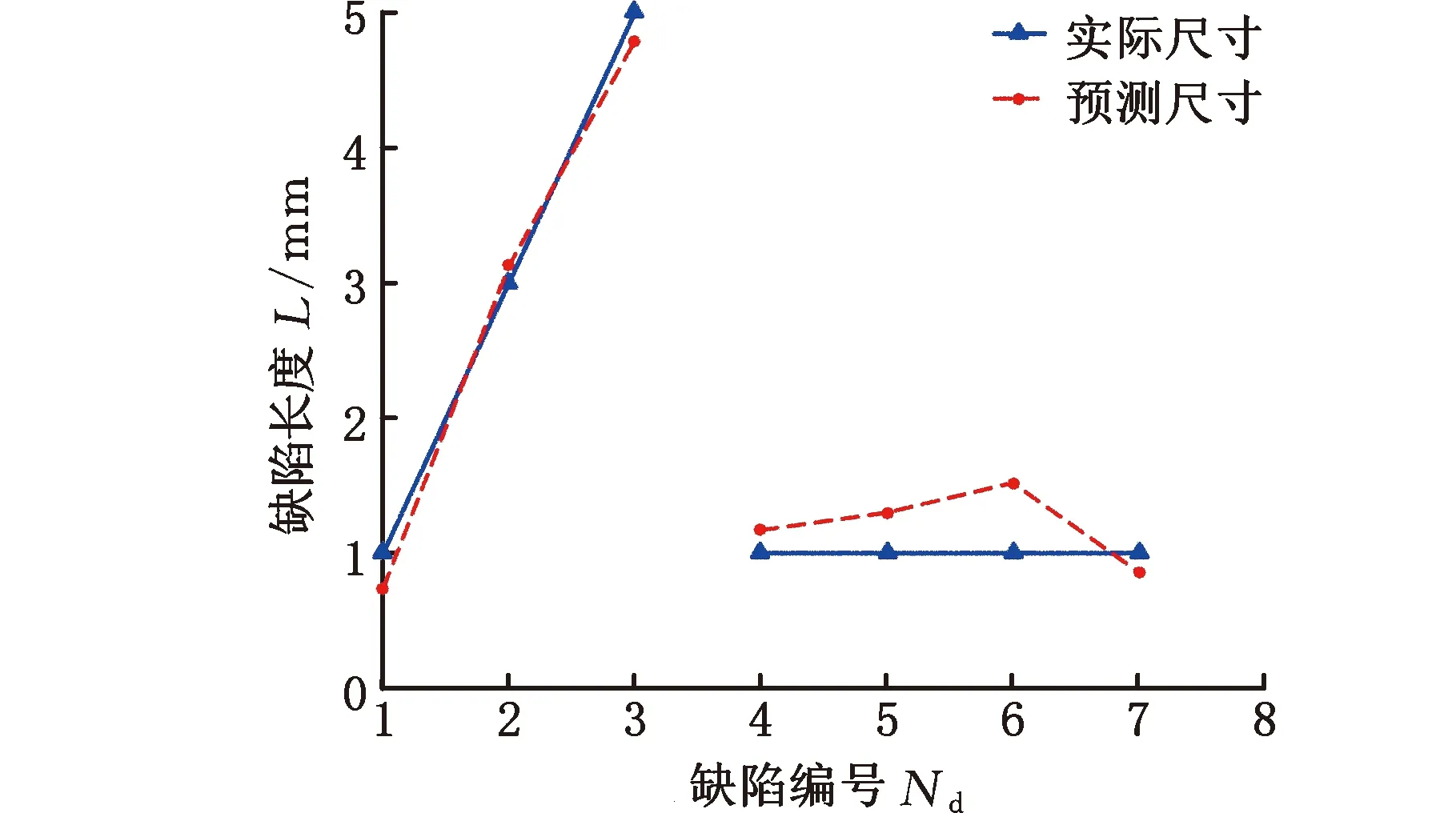
(a)长度反演结果

图12a、图12b、图12c分别对应7组缺陷特征值长度、宽度、深度模型的反演结果,其中实线是缺陷实际尺寸,虚线是预测的缺陷尺寸。整体而言,遗传算法优化参数后的SVM模型表现出较好的反演效果。其中,第7组特征值的反演效果明显优于第6组特征值的反演效果,因此对于磁异常极性相反的铁磁性夹渣缺陷,本文采用的特征值调整方法简单有效。剔除表3中第6组数据,计算每个缺陷长度、宽度、深度预测准确度的平均值发现,宽度的反演效果最好,平均预测准确度为90.67%;其次是深度,平均预测准确度为84.95%;最后是长度,平均预测准确度为84.08%。宽度和深度的预测效果和模型建立时相当,长度的预测准确度比模型建立时降低了11.79%,这是因为样本库中的缺陷长度范围为10～20 mm,而用于模型验证的缺陷长度范围为1～5 mm,验证模型与样本的差距过大导致长度模型预测准确度降低,但仍接近85%,说明经过参数优化的SVM算法对样本库之外的数据可表现出较好的预测能力。

3 结论

(1)优化参数的支持向量机(SVM)反演模型与默认参数模型相比,能够更加精确地反演缺陷尺寸。经过参数优化后,长、宽、深度的预测结果比默认参数的预测结果都有提高,尤其是长度和深度的反演效果有显著提高;优化后的反演效果,遗传算法比交叉验证法的预测精度更高。

(2)当缺陷与母材磁导率差异较大时(如高温合金表面的铁磁性夹杂),与空气槽产生的磁异常方向相反,弱磁检测信号在缺陷处产生向上凸起的磁异常,且磁异常特征幅值偏大,对该缺陷信号特征值幅值以及面积减半后进行反演,得到的结果准确度更高,提高了20%以上。

(3)优化参数的SVM反演模型不仅能够对已有的缺陷样本数据进行预测,对未加入样本库的缺陷也能进行预测。当预测模型与样本数据的差距过大时,会导致模型预测准确度降低,实例表明,预测准确度接近85%,说明经过参数优化的SVM算法对样本库之外的数据仍表现出较好的预测能力。