基于因果模型和多模态多目标优化的两阶段特征选择方法
王逸豪,黄敬英,范勤勤*
(1上海海事大学 物流研究中心,上海 201306; 2 浙江大学 医学院附属邵逸夫医院麻醉恢复室,浙江 杭州 310020)
在医疗领域,风险预测模型通常以某种疾病的病因为基础,通过分析多因素的危险水平来建立预测模型[1]。术中低体温是指人体在接受手术治疗中核心体温低于36 ℃的现象。术中低体温的发生会影响人体酶促反应效率和药物代谢时间,严重的会导致人体术后寒战、凝血功能异常、呼吸抑制等情况,有时甚至会导致死亡[2-3]。此外,术中低体温的发生概率较高(50%~70%)[4-5]。因此,降低术中低体温发生的风险十分重要[6]。
为降低术中低体温的发生,研究人员相继推出各种风险预测模型。文献[7]根据专家文献分析选取了7个危险因素来建立全麻手术患者的术中低体温评分方程,并使用外部数据对其进行验证,所得AUC(area under the curve,记作AUC)值为0.771,实验结果表明该方程具有良好的预测性能。文献[3]提出一种针对腹腔镜手术的低体温风险预测模型,该模型通过单因素和多因素的逻辑回归选取4个特征进行建模,实验结果AUC=0.791,表明该模型的拟合度中等偏上。文献[8]提出一种低体温风险预测模型,首先通过双变量相关分析对特征进行分析,然后使用后向删除不显著的特征,最终选取5个特征来建立逻辑回归模型;通过64名手术患者测试集的测试,该模型所得AUC=0.85,实验结果表明模型的拟合度较好。
已有研究表明,特征选择会极大影响机器学习模型的预测精度。传统的特征选择方法主要有4种[9]:封装式、过滤式、嵌入式和混合式方法。为解决特征选择问题,文献[10]提出一种基于信息增益与皮尔森相关系数的2D自适应特征选择算法,该方法以信息增益为特征辨识度,并以皮尔森相关系数作为特征的独立性,选出在2D坐标空间中对分类任务贡献大的特征作为特征子集;实验结果证明,与经典特征选择算法相比,所提方法能在高维小样本的基因表达数据上选出有效的特征子集。文献[11]根据最大信息系数理论提出一种基于特征排序和近似马尔科夫毯的两阶段混合式特征选择方法,从而得到特征相关性与冗余性的关系。文献[12]通过众包学习将多种特征选择方法的结果根据可靠性集成在一起,实验结果表明该方法能够提高特征选择的有效性。为了避免特征选择陷入局部最优[13],研究人员使用进化算法去解决特征选择问题。文献[14]提出一种融合遗传算法和乌燕鸥算法的封装式特征选择方法,该方法使用遗传乌燕鸥算法对特征和支持向量机两个参数进行同时优化,从而提高预测模型的分类精度。文献[15]提出一种改进的多目标森林优化算法来解决多目标特征选择问题,实验结果表明,所提算法在特征数量和分类错误率方面都优于其他多目标特征选择方法。文献[16]提出一种基于特征属性的新型自学习封装式特征选择方法,该方法利用先前特征子集的SHAP值指导元启发算法的搜索过程,故具有较高的搜索效率。文献[17]提出一种将高维特征选择任务转化成几个低维特征选择任务的多任务粒子群算法,通过低维特征选择任务之间的知识迁移找到最优特征子集。
由于以上研究都尚未将特征选择当作是一个多模态多目标优化问题,故它们无法给出更多等效的特征子集。相比于普通的多目标优化问题,多模态多目标优化不仅需要在目标空间找到好的帕累托前沿逼近,还要在决策空间找到足够多的等价帕累托解[18]。虽然特征选择的主要任务是找出特征子集以降低维度,但这些特征子集可能存在多组等效的情况。为解决以上问题,Kamyab等[19]将多模态优化算法用于求解特征选择问题,结果表明多模态优化方法找到的解决方案比单模态方法更具多样性。Yue等[9]则使用一种多模态多目标优化算法来进行特征选择,实验表明多模态多目标优化算法可以降低特征提取成本。Jha等[20]基于特征间互信息与冗余度等因素,使用一种基于环形拓扑结构的多模态多目标优化算法进行过滤式的特征选择,选择出具有最小冗余和最大相关的特征子集;实验结果显示,相比于其他特征选择方法,所提算法不仅能提供更多数量的等效特征子集,而且具有更好或相似的预测精度。
虽然以上研究使用多模态多目标优化算法来进行特征选择,但是它们都没有考虑高维特征选择问题。为解决现有多模态多目标优化算法无法解决高维特征选择问题,本文提出一种基于因果模型和多模态多目标优化的两阶段特征选择方法(two-stage feature selection method based on causal model and multimodal multi-objective optimization,TSFS-CMMMO)。在所提算法中,首先通过因果模型删除高维数据样本中的不相关特征进行降维,然后使用多模态多目标进化算法对降维后的数据特征再次进行特征选择,最后将TSFS-CMMMO与深度森林算法进行结合,用于术中低体温风险预测。实验结果表明,相比于传统特征选择方法,所提算法不仅能够提供多种可行方案,还能克服实际应用中数据特征不易获取的问题。同时,相比于基于多模态多目标进化算法的特征选择方法,所提方法能够大大降低多模态多目标优化算法的求解难度,从而获得更多的等效解集。
1 相关工作
1.1 因果模型
因果模型可以表示数据中的因果关系[21]。真正快速因果推断[22](really fast causal inference,RFCI)算法是由Diego等提出的一种因果模型。在因果充分性假设难以满足的条件下,满足因果马尔可夫和因果忠诚性假设就可以刻画高维数据中各变量的依赖关系。
RFCI算法主要包含4个步骤:1)构造所有变量的完全图;2)使用d-分离法对三元组中的节点vi和vj进行vz节点下的独立性检测(如图1所示),并删去多余边确定开放三元组〈vi,vj,vk〉和分离集sepset(记作SS);3)根据开放三元组〈vi,vj,vk〉中的vj是否为碰撞点来确定v型结构;4)尽可能给更多的边定向。RFCI算法的具体流程如算法1所示。

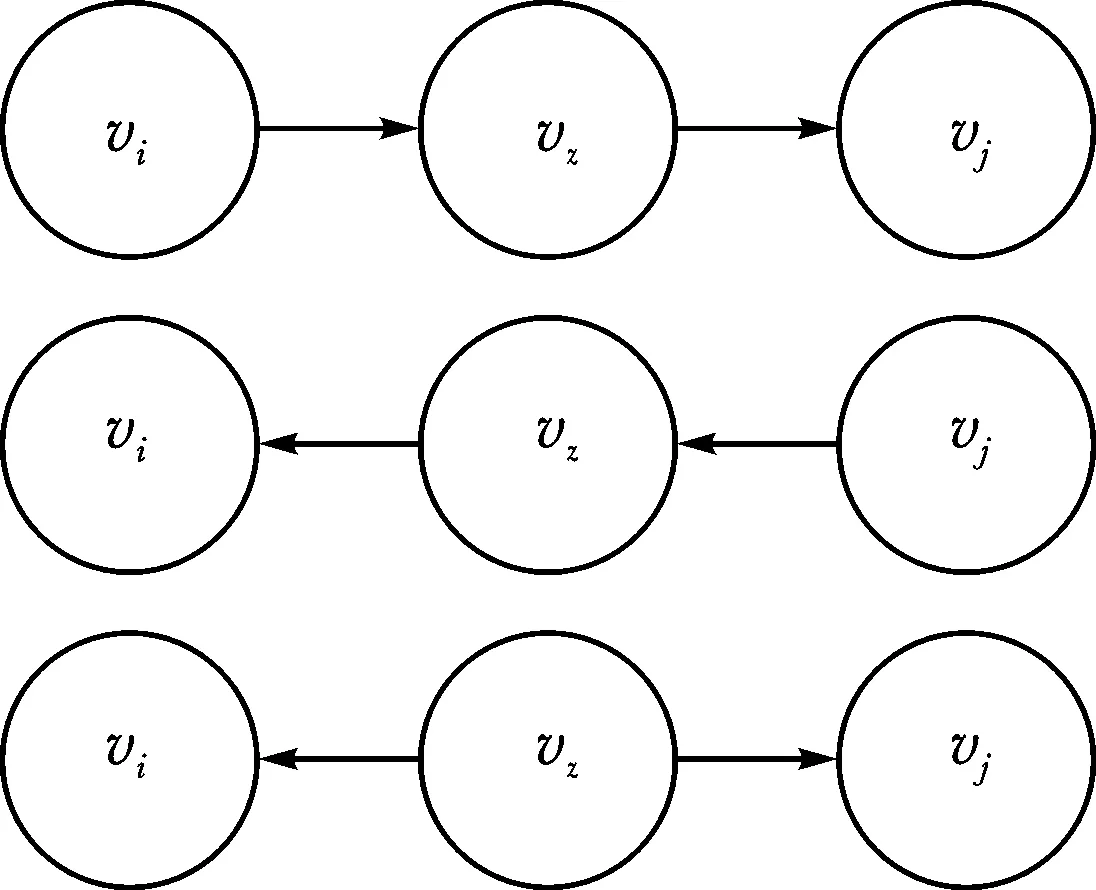
图1 vi⊥vj|vk的3种d-分离示意图Fig.1 Three d-separation diagrams of vi⊥vj|vk
1.2 基于自组织的多目标粒子群算法
基于自组织物种生成的多目标粒子群算法[23](self-organized speciation based multi-objective particle swarm optimizer,SSMOPSO)是一种结合了非支配排序算法和特殊拥挤距离的多模态进化算法[17]。它根据相似性将种群分为多个子种群,在求解多模态多目标优化问题上有较好表现。
在SSMOPSO算法中,首先,建立个体最优存档(private optimal archive,POA,记作POA),POA(i)代表当前第i个粒子的最优位置,并根据个体的非支配排序选择物种种子(记为nbest),预设半径R确定物种大小及包含的个体。然后,将多个子种群作为不同物种,同时向多个最优方向进化,Pi(t)代表第t代第i个粒子,每个粒子i的速度向量s和位置l根据(1)式和(2)式[23]迭代更新:
si(t)=Wsi(t-1)+c1r1(lpbest-li(t))+
c2r2(lnbest-li(t)),
(1)
li(t)=li(t-1)+si(t)。
(2)
式中:W表示惯性权重;c1和c2为2个加速因子;r1和r2为服从[0,1]均匀分布的2个伪随机数;pbest代表个体最佳粒子。最后,各子种群并行搜索得出多个帕累托等价解集。SSMOPSO的伪代码如算法2所示。

1.3 深度森林

图2 多粒度扫描示意图Fig.2 Schematic diagram of multi granularity scanning
2 基于因果模型和多模态多目标优化的两阶段特征选择方法
为了解决现有多模态多目标优化算法无法求解高维数据特征选择的问题,本文提出一种基于因果模型和多模态多目标优化算法的两阶段特征选择方法:首先使用因果模型对高维数据特征进行降维,然后使用SSMOSPO算法对降维后的数据特征进行多模态特征选择,从而克服多模态多目标进化算法对高维特征搜索能力不足的问题,最终获得多组等效的特征子集。
图4是特征选择中多模态特性的示意图,图中虚线代表多目标优化问题的帕累托前沿。假设x1、x2、x3、x4、x5表示原始数据特征,填充黑点的方框表示被选择的特征,而空白方框是未选择的特征。在图4中,{x1,x3}和{x2,x4}是选中的两组不同特征子集,它们的分类错误率和特征数量相同,因此它们是一组具有多模态特性的等效特征子集。

图4 特征选择中的多模态特性示意图Fig.4 Schematic diagram of multimodalcharacteristics in feature selection
基于TSFS-CMMMO的深度森林算法主要包含两个部分,即数据特征两阶段选择和深度森林算法建模。在使用因果模型进行特征选择时,所提算法先对输入的原始特征使用证据权重[26](weight of evidence,WOE,记作WE)进行编码处理。对于第h个类型,其正负样本分布比值的对数计算公式为
(3)
式中:py1表示该类型在负类样本分布;py0表示该类型在正类样本的分布;Bh表示该类型中负类样本的数量;BT为总样本中负类样本的数量;Gh表示该类别中正类样本的数量;GT为总样本中正类样本的数量。
在使用多模态多目标进化算法进行特征选择阶段时,因为所选多模态多目标进化算法不能直接求解特征选择问题,所以每个决策变量的取值范围设为[0,1],同时设置0.5为选择阈值,即当某个决策变量的值大于等于0.5代表这个位置对应的特征被选中;小于0.5则代表这个位置对应的特征被剔除。为直观解释个体编码和解码过程,其过程如图5所示。粒子维度等于特征数量(在本例中特征数量假设为9),从图5中可以看出, {x1,x3,x5,x6,x8,x9}为选中特征组成的子集。对于原始数据特征F,选中的特征FS和未选中特征FNS满足(4)式和(5)式:

图5 粒子与特征选择的示意图Fig.5 Shcematic diagram of particle and feature selection
F=FS∪FNS,
(4)
FS∩FNS=∅。
(5)
基于TSFS-HMMMO的深度森林算法如图6所示,整体实现步骤如下:

图6 基于TSFS-HMMMO的深度森林算法框架图Fig.6 Framework of deep forest algorithm based on TSFS-HMMMO
步骤1,输入原始数据;
步骤2,对手术类别特征进行WOE编码;
步骤3,使用因果模型对原始数据进行特征选择;
步骤4,基于步骤3,使用SSMOPSO算法对降维后的数据特征进行再次选择;
步骤5,根据步骤4得到的数据特征,使用深度森林算法进行建模;
步骤6,判断是否满足搜索停止条件,满足则进行步骤7,不满足则返回步骤4;
步骤7,输出所有满足条件的搜索结果,即具有多模态特性的特征子集。
3 实验结果比较与分析
3.1 数据集
本文使用的数据集为实际术中低体温数据,共有295个样本,特征数量为11,包含发生术中低体温和未发生术中低体温两类结果。其中术中低体温的总体发生率约为67.80%。经过数据预处理,删除其中数据缺失过多的样本,最终使用其中290个数据样本。表1给出术中低体温数据集的详细情况。

表1 术中低体温数据集的所有特征Tab.1 All features of intraoperative hypothermia data set
3.2 实验设置
本文将数据集按比例随机分为训练集(75%)和测试集(25%),并使用1-AUC来对算法的分类能力进行评价。所有错误率均通过五折交叉验证法产生。
在基于TSFS-HMMMO的深度森林算法中,SSMOPSO算法的物种半径设置为自变量范围[0,1]的5%,即0.05[27];种群规模和最大适应度评估次数分别设为300和30 000。所有实验均使用相同参数的深度森林算法作为分类器,其中随机森林和完全随机森林均包含100个决策树[28]。为确保实验的公平性,本文所有实验都在Intel Core i7-10700 CPU @2.90 GHz运行环境下,并使用MATLAB 2021a和Python 3.7来进行计算。
3.3 实验结果对比分析
3.3.1 算法结果比较
为验证所提方法的特征选择能力,将其分别与2种方法进行比较,即未进行特征选择的深度森林算法和基于因果模型的深度森林算法。
所提算法首先使用因果模型(即RFCI算法)来对数据特征进行分析;其输出的特征因果关系如图7所示,可以看出术前体温(x2)、BMI(x6)等能直接或者间接影响术中低体温情况的发生。根据因果模型,可以剔除与结果x12不相关的x3、x4和x5等特征,即病患性别、病患年龄和ASA分级。因此,术中低体温可由x1、x2、x6、x7、x8、x9、x10和x11等8个特征表示。根据以上8个特征,本实验分别使用深度森林算法和基于因果模型的深度森林算法来对其进行建模,实验结果见表2。

表2 3种方法的实验结果Tab.2 Experimental results of the three methods
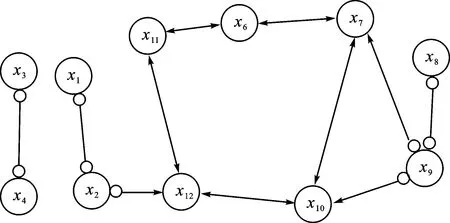
图7 术中低体温风险的因果模型Fig.7 Hausal model of intraoperative hypothermia risk
在因果模型得到的特征选择结果基础上,所提TSFS-HMMMO算法利用多模态多目标进化算法对特征再次进行选择;并将特征数量和分类错误率作为2个优化目标(结果见表2)。从表2可知,使用深度森林算法对原始数据(11个特征)进行建模,不仅使用特征数量最多,而且错误率较高。对于基于因果模型的深度森林算法而言,其使用8个特征来进行建模,相比于原始深度森林算法,其在特征数量和错误率两方面都有较好表现。另外,从表2可知,在特征数量≥2的情况下,所提算法在特征数量和错误率方面的表现均要优于未进行特征选择的深度森林算法和基于因果模型的深度森林算法。这说明TSFS-HMMMO算法有较好的特征选择能力,主要原因是所提TSFS-HMMMO算法不仅使用因果模型剔除了不相关的特征,而且还使用多模态多目标进化算法得到更多的等效特征子集。
此外,相比于其他2种方法,TSFS-HMMMO算法可以通过多组等效的特征子集进行建模。例如,当选择特征{x2,x6,x7,x8,x10,x11}或特征{x1,x2,x6,x7,x8,x11}进行建模时,它们的特征数量都为6,分类错误率都是0.22。在术中低体温数据集中,x1是术前是否发生低体温,x10是失血量。术前是否发生低体温可以直接通过测量体温获得,而失血量这一特征需要专家在术前根据病人手术类型估计得到。如果只选择6个特征进行建模预测,显然术前是否发生低体温比失血量这一特征更容易获得,所以决策者可以选择特征获取成本低的{x2,x6,x7,x8,x10,x11}而不是{x1,x2,x6,x7,x8,x11}进行建模。同时,从表2可以看出,TSFS-HMMMO算法可以在高维空间找到多组具有多模态特性的特征子集,为决策者提供多种建模方案,从而降低了术中低体温风险预测模型的建模成本。
如上所述,特征数量和分类精度通常是2个冲突的目标,所提算法得到的Pareto前沿逼近见图8。从图8可知选择特征数量与分类错误率呈现负相关,这表明决策者需要在特征数量和分类精度之间进行平衡。
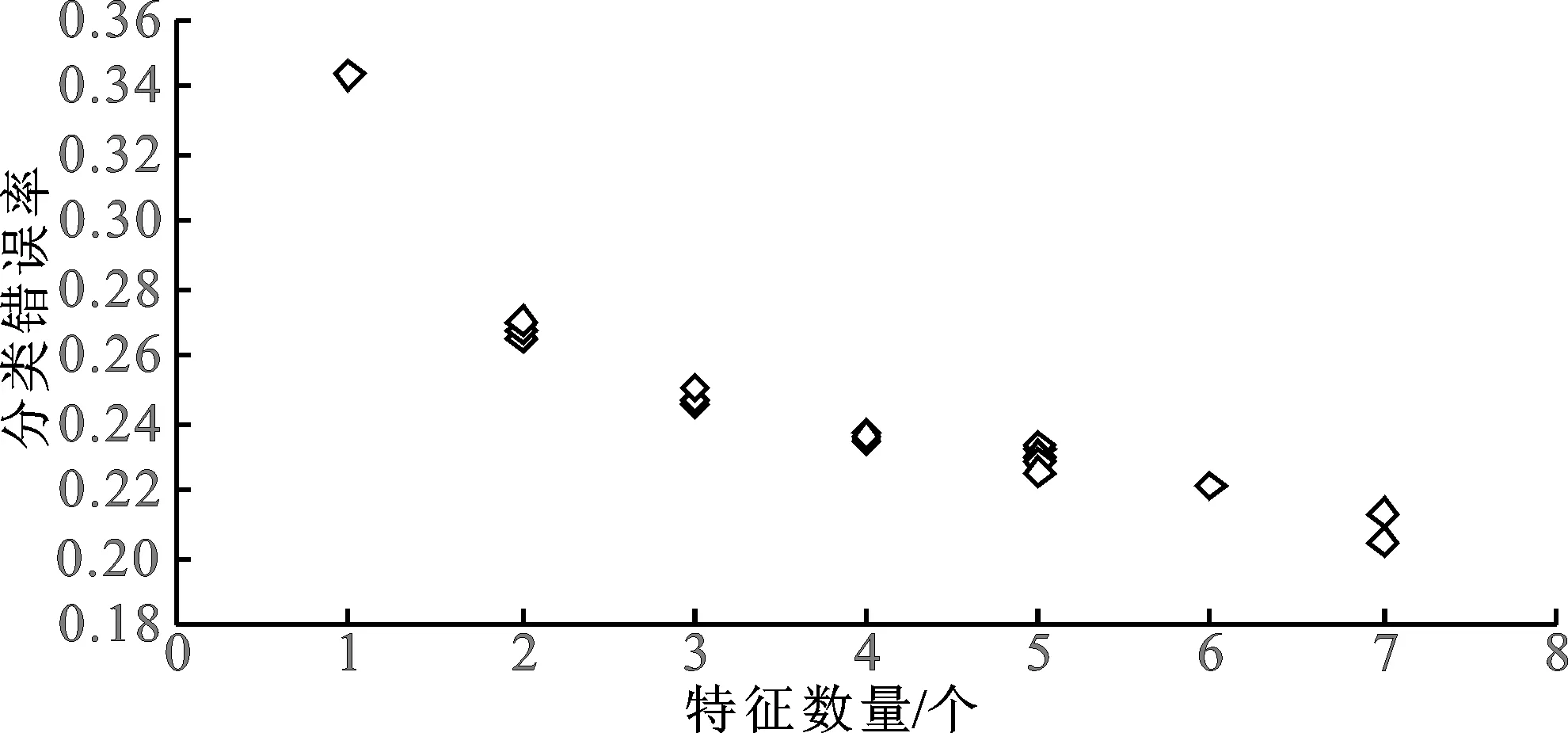
图8 结合TSFS-HMMMO的深度森林算法所得Pareto前沿Fig.8 Pareto front obtained by the deep forest algorithm combined with TSFS-HMMMO
综上所述,所提算法不仅具有较强的数据特征选择能力,而且能够提供多种等效的特征子集来降低建模成本。因此,TSFS-HMMMO是一种提高术中低体温风险预测能力的有效方法。
3.3.2 算法分析
为验证本文提出的TSFS-HMMMO算法在高维数据上的特征选择能力,将去除因果模型的TSFS-HMMMO算法用于术中低体温数据的特征选择,其结果如表3所示。由表2可知,当特征子集为{x2,x6,x7,x8}时,基于TSFS-HMMMO的深度森林算法的分类错误率为0.24;而由表3可知,当不使用因果模型和特征子集为{x2,x5,x7,x8}时,基于SSMOPSO的深度森林算法的分类错误率为0.25。由上可知,在特征数量相同的情况下,基于TSFS-HMMMO的深度森林算法的分类错误率更低。这是由于因果模型剔除x5等不具备良好分类能力的特征,避免了多模态多目标优化算法在高维决策空间上进行搜索。此外,从表2可知,当特征子集为{x2,x6,x7,x11}时,基于TSFS-HMMMO的深度森林算法的分类错误率为0.24;但表3显示,当特征子集为{x2,x3,x6,x7,x11}时,基于SSMOPSO的深度森林算法的错误率也为0.24。这说明代表性别的特征无法提高分类器的性能,在分类错误率相同的情况下,使用基于因果模型和多模态多目标进化算法两阶段特征选择方法要好于只使用多模态多目标进化算法的特征选择方法。

表3 基于SSMOPSO算法的特征选择实验结果表Tab.3 Experimental results of feature selection based on SSMOPSO
为进一步说明本文算法的有效性,对比TSFS-HMMMO和SSMOPSO 2种算法找到的等效特征子集数量(如图9所示)。从图9可以看出,在特征数量较少时,相比于SSMOPSO算法,TSFS-HMMMO方法能找到更多的等效特征子集。这是由于因果模型缩小特征空间,使得多模态多目标优化算法可以有效地进行搜索。但是,在高维情况下,SSMOPSO算法反而能找到更多的特征子集,其主要原因可能是降维后的搜索空间存在的等效解变少。比如,当从11个特征中挑选8个特征时,可能会存在更多的等效特征子集。因此,相比于SSMOPSO,TSFS-HMMMO方法可以在缩小的搜索空间内找到更多的特征子集,这缓解了多模态多目标进化算法求解高维数据特征能力弱的问题。

图9 多模态特征子集数量对比图Fig.9 Comparison of the number of multi-modal feature subsets
4 结语
本文针对现有大多数多模态多目标进化算法在高维特征选择问题上存在搜索能力不足的问题,提出一种基于因果模型和多模态多目标优化的两阶段特征选择方法(TSFS-HMMMO)。在本文TSFS-HMMMO算法中,首先使用因果模型分析特征变量之间的因果关系,剔除不相关特征以减小特征搜索空间的大小;然后使用多模态多目标进化算法搜索特征子集;最后使用深度森林算法对降维后的术中低体温数据进行建模。实验结果表明,该方法具有以下优点:1)克服了多模态多目标算法在高维特征选择问题中搜索能力不足的问题;2)提供多组等效的特征选择方案,降低了建模的特征获取成本;3)可以为决策者提供有效决策支持。

