简约而不简单平和而不平淡——2023 年高考新课标Ⅰ卷第22 题的解法探究与纵横探索

江苏省徐州市第一中学 (221140) 许丽

题目(2023 年高考新课标Ⅰ卷第22 题)在直角坐标系xOy中,点P到x轴的距离等于点P到点的距离,记动点P的轨迹为W.

(1)求W的方程;

(2)已知矩形ABCD有三个顶点在W上, 证明: 矩形ABCD的周长大于

1. 问题分析

第(2)问叙述非常简练,但是包含众多变化,三点的位置不明确.

实际上的构图就是过曲线上一点作两条互相垂直的直线,这在圆锥曲线中是无比寻常的构图方式,解决起来是否也会得心应手呢?不妨设A,B,D三点在W上, 且AB⊥AD,如图1.

图1

2. 解法探究

视角1 设斜率

这是一个双变量求最值问题. 我们可以采用主元法,先将a看成变量,处理的基本思路有两种.

思路1(函数的性质)考虑绝对值函数

利用单调性确定其最小值:

注: 以上去绝对值后得到关于k的式子,都只展示了一种求最值的做法,其实都可以用基本不等式、均值不等式或导数进行解决.

视角2 设点

3. 考题溯源

与本题最有渊源的就是下面这道竞赛题,改正方形为长方形,提高了运动的灵活性,变面积为周长的探求,增加了模型的复杂度.

竞赛题源(1998 年上海市数学竞赛试题)已知抛物线y=x2上有一个正方形的三个顶点A,B,C,求这种正方形面积的最小值.

事实上,这类问题主要研究的是过曲线上同一点且互相垂直的两弦,是圆锥曲线中的一类经典问题,常考常新.

课本题源(选择性必修第一册教材习题)在平面直角坐标系xOy中,已知直线y=x-2 与抛物线y2=2x相交于点A,B. 求证:OA⊥OB.

本题中的直线若换成y=k(x-2)仍然有OA⊥OB成立,换句话说就是满足OA⊥OB的直线AB过定点(2,0).下面这道高考题就把这种过定点的结论隐藏在|DQ|为定值的探究中.

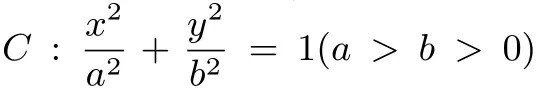
(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足. 证明: 存在定点Q,使得|DQ|为定值.

通过溯源,更显命题者的匠心,考题看似亲切小巧,实则内涵丰富,反映出新高考“平和中有新意、灵活中见潜力、实践中出真知”的命题追求,意在引导中学把教学重点从总结解题技巧转向应用知识解决问题,着力发展学生的核心素养.

4. 纵横探索

推广到一般的抛物线,可得如下命题:

命题3 的证明留给有兴趣的读者.