考虑落角约束和气动不确定性的固定时间制导控制一体化设计方法

胡诚伟，韦 悠，汪学平

(西安现代控制技术研究所，陕西 西安 710065)

0 引言

现代战争中更加能动的战场战术和精度要求的提高使得经典控制系统设计方法在很多应用中不能满足要求。通常来说,制导系统和控制系统可以通过解耦分为两个独立的子系统,从而形成典型的两回路控制方案[1-2]。基于这种设计思路,已经有文献提出了包括比例导引[3-4]、鲁棒制导律[5-6]和滑模制导律[7-8]等多种有效的制导控制方法。上述方法虽然已成功应用于目标拦截,但采用分离设计的制导和控制系统,其拦截高机动目标时性能可能会严重下降。

为了提高导弹的杀伤效能,制导控制一体化设计已成为战术导弹制导与控制系统设计的新趋势。一般来说,现有制导控制一体化设计方法可以分为基于自动驾驶补偿的制导律设计方法和完全制导控制一体化设计方法[9]。对于第一类方案,通常将自动驾驶仪假设为一阶或二阶环节,然后在制导律设计中加入补偿来处理自动驾驶仪带来的响应滞后[10-11]。尽管这些算法能够实现目标拦截,但其性能严重依赖于对自动驾驶仪近似估计的准确性。然而,对于大空域机动的导弹,其空气动力学特性本身就存在着较大的不确定性,这使得自动驾驶仪很难被精确地近似为简单的一阶或二阶环节。而完全制导控制一体化设计方法能够避免对自动驾驶仪的近似估计,直接针对完全非线性导弹动力学模型设计制导控制方法,其中典型的方法包括反馈线性化方法[12]、状态依赖Riccati方法[13]、θ-D方法[14]、模型预测静态规划方法[15]和有限时域最优控制[16]。然而,完全制导控制一体化设计方法计算较为复杂,且大都无法保证闭环系统的鲁棒性[17]。

由于导弹制导和控制系统具有严格的反馈形式[18],因此反步设计思想在制导控制一体化设计中也被广泛应用。然而,在反步设计过程中对虚拟控制量进行重复微分会导致“微分膨胀”问题[19]。为了解决这个问题,动态面控制技术被用于制导控制一体化设计中。文献[20]针对慢机动目标,基于自适应动态面控制给出了一种制导控制一体化设计方法。文献[21]通过引入了模糊系统来估计和补偿不确定性,提出了一种基于自适应模糊动态面的制导控制方法。文献[22]提出了一种二阶滑模微分器来估计虚拟控制量的导数,实现了考虑气动不确定性和落角约束的制导控制一体化设计。然而,上述基于反步控制和动态面思想给出的方法只能实现半全局渐近最终有界稳定,而非有限时间稳定[23]。因此研究有限时间收敛的制导控制一体化设计方法具有重要的实际意义。作为有限时间稳定性理论的扩展,固定时间稳定性引起收敛时间上界不依赖于初始条件而被广泛的关注。然而,固定时间制导方法仅适用于二阶系统,无法直接应用到导弹的制导控制一体化设计问题。

基于上述分析,文中研究考虑落角约束和气动不确定性的固定时间制导控制一体化设计问题。基于反步法提出了固定时间滑模制导控制一体化设计方法,并借助于固定时间微分器解决了传统反步设计中存在的“微分膨胀”问题,最终实现了闭环系统的半全局固定时间一致最终有界稳定。主要价值在于:1)提出了一种固定时间制导控制一体化设计方法,并实现了不受初始条件影响的半全局固定时间一致最终有界稳定;2)在制导控制一体化设计中考虑了目标机动不确定性和导弹气动不确定性,使得所提出方法更加适用于实际应用。

1 问题描述和预备知识

考虑铅垂面内落角约束的制导控制一体化设计问题。图1为导弹与目标相对运动示意图,其中VM和VT为导弹和目标速度且满足VT/VM>1;aM和aT为导弹和目标垂直于速度方向的加速度;γM和γT为导弹和目标弹道倾角;r和λ分别表示导弹与目标之间的相对距离和视线角。为简单起见,导弹和目标被视为匀速运动的点质量。

图1 导弹与目标相对运动Fig.1 Relative motion between missile and target

导弹和目标间相对运动可以表示为:

(1)

(2)

(3)

(4)

(5)

文中所研究的带落角约束的制导控制一体化设计问题可以表述为设计控制输入δz使得导弹以期望视线角λd与目标交会。

为了给出主要结果,考虑以下系统:

(6)

(7)

2 集成制导与控制律设计及稳定性分析

2.1 制导控制一体化设计

为了给出制导控制一体化设计方法,需借助于以下假设:

基于上述假设,下面将根据典型的反步设计过程逐步给出制导控制方法。

步骤1:令s1=λ-λd,s1对时间求导可得:

(8)

其中,Δ1=-aT/VT被视为外部干扰,其上界d1>0,即|Δ1|≤d1。

为式(8)选择以下虚拟控制律:

(9)

其中:k1,c1,p,q是正实数;ρ1≥d1。

(10)

步骤2:令s2=Vλ-Vλ,d,s2对时间求导得出:

(11)

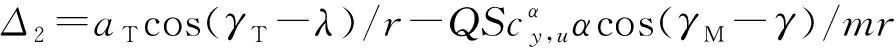
(12)

其中:k2和c2为正数;ρ2≥d2。引入新状态变量αd其动力学由式(13)给出:

(13)

其中τ2>0为时间常数。

步骤3:令s3=α-αd,并对s3求导得出:

(14)

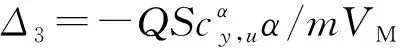
(15)

其中k3和c3为正数,且ρ3≤d3。引入新状态变量ωd,其动力学满足:

(16)

其中τ3>0为时间常数。

步骤4:令s4=ωz-ωz,d,并对s4求导得:

(17)

对于子系统式(16),考虑控制律:

(18)

其中:k4和c4是正数;ρ4≥d4。

2.2 稳定性分析

给出稳定性分析,以证明提出方法具有半全局固定时间稳定性。首先定义以下误差变量:

(19)

对于使用文中所提控制律的闭环系统,存在足够大的正常数ki,ci(i=1,2,3,4)、足够小的正常数τi(i=1,2,3)和正奇数p,q,满足p>q且(p+q)/2是正奇数,使得闭环系统是半全局一致最终有界的,同时在任意初始条件下所有误差均可以在固定时间Ts内稳定在原点任意小的邻域中。

考虑以下李雅普诺夫函数:

(20)

选择设计参数使得:

令

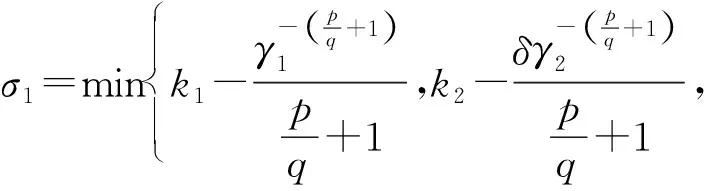
(21)

(22)

(23)

计算所定义李雅普诺夫函数的导数。

假设Ω>0为闭环系统的初始条件的边界,即V1(0)≤Ω。因此总可选择合适的参数,使得以下不等式成立:

(24)

因此,{V1≤Ω}是一个不变集,并且对于所有t>0,V1(t)≤Ω都成立,这表明整个闭环系统是最终有界的。闭环系统可以固定时间内稳定在原点的一个小邻域中,收敛时间上界为:

(25)

3 仿真结果

3.1 参数设置

假设空气动力系数相对于标称值有30%的不确定性。不失一般性,设计参数可选择为p=9,q=6,k1=1,k2,=2,k3=5,k4=10,ci=0.08(i=1,2,3,4),τi=0.01(i=1,2,3)。导弹和目标的初始条件见表1。

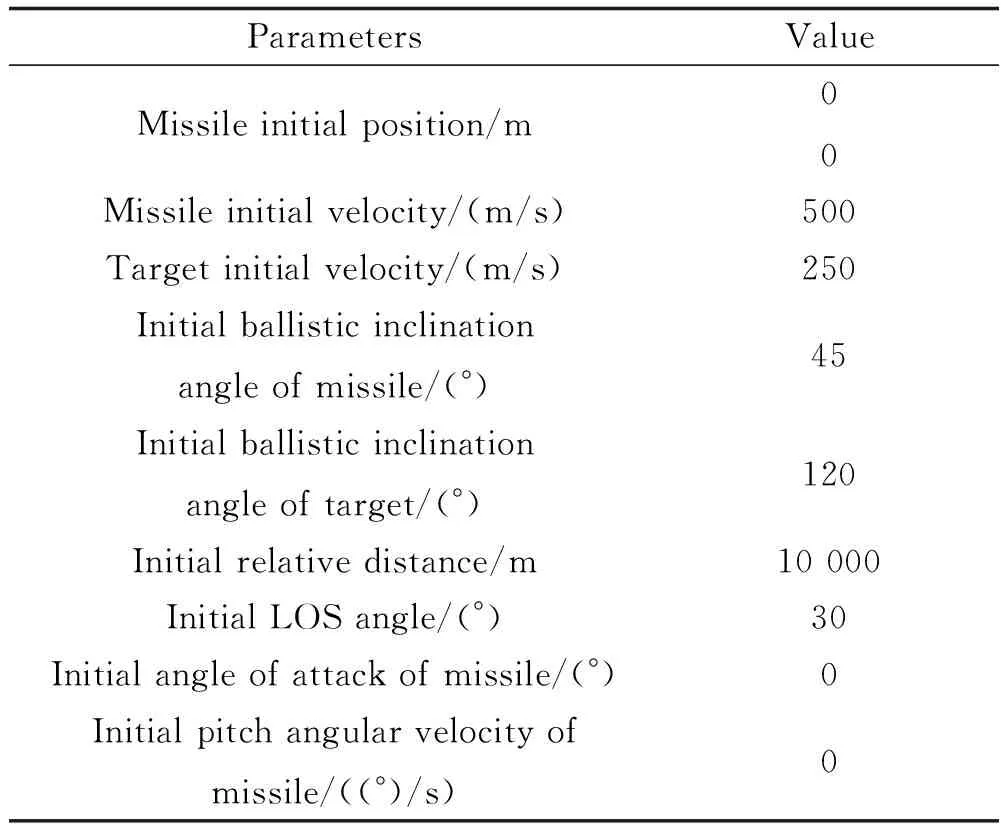
表1 初始条件Table 1 Initial condition

3.2 不同落角约束仿真

给出不同落角约束下机动目标拦截的仿真结果。期望落角γd分别选择为0°、30°、60°和90°。仿真结果如图2所示。

图2 不同落角约束下的仿真结果Fig.2 Simulation result of different impact angle constraint

末端脱靶量和落角误差如表2所示。从表2和图2可以看出,文中所提出的制导控制一体化设计方法针对不同落角约束下的目标拦截问题,都能够取得较小的脱靶量和落角误差。具体而言,在所有拦截场景中落角误差和脱靶量分别小于0.004°和0.4 m。从图2还可以看出,在拦截过程中舵偏角在允许的最大值范围内且较为平滑。

表2 脱靶量与落角误差Table 2 The miss distance and impact angle error

3.3 对比仿真

为了突出文中所提出的制导控制一体化设计方法的优越性,给出了与非奇异终端滑模制导律文献[7]和固定时间非奇异终端滑模制导律文献[8]的对比仿真。加速度约束为|aM|≤200 m/s2,期望落角为γd=45°仿真结果如图3所示。

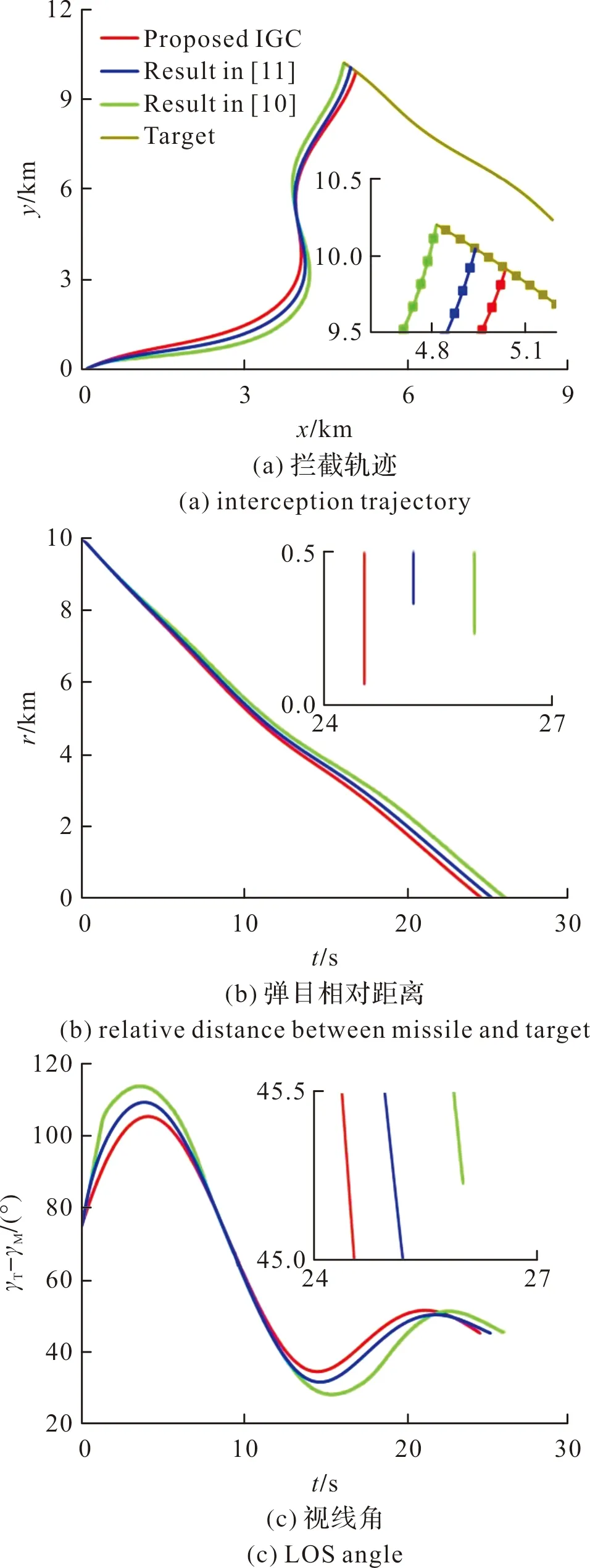
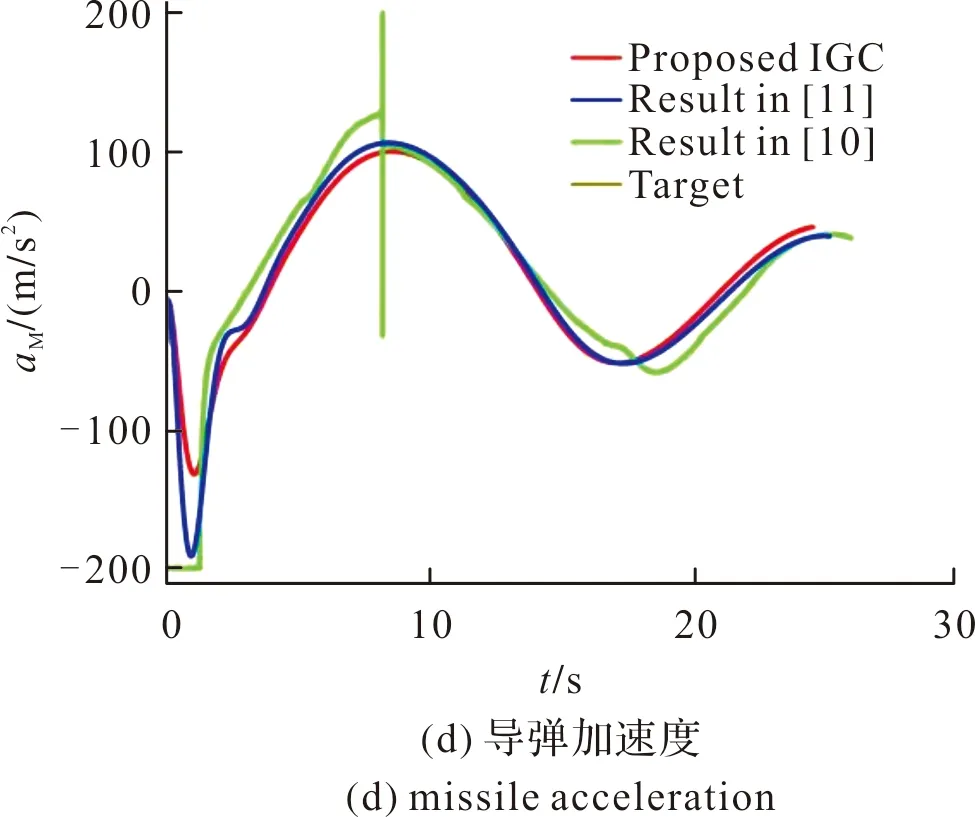
图3 对比仿真Fig.3 Comparative simulation

从图中可以看出与文献[7-8]中提出的方法相比,文中所设计的制导控制一体化方法能够以相对更小的加速度和更短的攻击时间获得相对较高的命中精度。

4 结论

文中针对考虑气动不确定性和落角约束的机动目标拦截问题,基于固定时间稳定性理论提出了一种制导控制一体化设计方法。利用典型的反步设计思想构建了滑模控制器,实现半全局固定时间一致最终有界稳定;同时通过引入固定时间微分器避免了典型反步设计存在的“微分膨胀”问题;并给出了李雅普诺夫函数框架下的稳定性分析。仿真结果与对比实验充分证明了文中所提出的制导控制一体化设计方法的有效性。