基于零和微分对策的非仿射导弹拦截系统制导律设计

田辈辈，刘 奇，袁斐然

(1 焦作大学机电工程学院，河南 焦作 454003；2 航空电子系统综合技术重点实验室，上海 200233)

0 引言

导弹拦截系统[1-3]在国防领域中举足轻重。制导律作为导弹拦截系统的关键部分,直接影响导弹性能并决定导弹能否成功拦截目标。随着攻防对抗形势的日益复杂,为了提高生存能力,目标可能采取更加隐蔽、多变的机动方式进行突防,因此,发展新型制导方式迫在眉睫。

近年来,将制导与现代控制理论相结合,形成诸如滑模制导[4-5],反步制导[6-7],自适应制导[8-9]等现代制导策略,并且取得了很好的效果。文献[10]针对制导拦截系统,设计了一类固定时间终端滑模制导策略,利用固定时间扩张状态观测器补偿目标机动,实现目标的拦截。考虑状态和输入约束;文献[11]基于反步法自适应动态规划技术,设计了一类自适应复合制导方法,实现了导弹在保证约束条件的前提下,对目标的精确拦截。上述制导策略虽然成功实施,在实际制导过程中,受战场环境等因素的影响,目标机动往往很难测量,这给制导律的设计带来了困难。

微分对策[12-13]是研究双方或多方冲突对抗或者竞争问题的有效工具,将博弈论的基本原理应用于最优控制中,研究多个控制输入在系统中的动态决策过程,控制的结果致使一方受益的同时另一方造成损失,被广泛应用于制导系统中,将导弹和机动目标视为对抗双方,考虑目标机动最坏情况下的制导策略,能够有效降低对目标机动信息的依赖。为此,文献[14]提出了一种基于事件触发的微分对策制导方法,考虑目标最坏逃逸方式,实现对目标拦截的同时降低导弹的通信负担;考虑目标携带防御武器的情况,文献[15]将其视为三方博弈问题,构造融合脱靶量和需用过载性能指标,设计微分对策制导策略,使得导弹能够避开防御武器并击中目标;针对多约束制导系统,文献[16]提出了一类复合微分对策制导方法,实现了导弹对目标的成功拦截。

然而,上述文献考虑的都是仿射系统,在实际系统中非仿射系统也是大量存在的,针对非仿射系统控制策略研究具有实际意义[17]。文献[18]针对具有多约束受限的非线性非仿射系统,提出了固定时间自适应神经网络跟踪控制方法;文献[19]针对一类具有内部动态和外部扰动未知以及非对称输入饱和约束的非仿射系统,提出了一种自抗扰反演控制方法。在未来战场中,攻防对抗必然更加复杂,当制导系统对制导策略呈现非线性时,针对仿射制导系统的研究显然不足以应对,因此,发展针对非仿射制导系统的研究迫在眉睫。

综上所述,文中针对非仿射导弹拦截系统,结合微分对策技术及积分自适应动态规划技术,提出了一类新的制导策略。主要创新点如下:

1) 与文献[4-11]所考虑的仿射导弹拦截系统不同,文中考虑的是更具一般性的非仿射导弹拦截系统,当前鲜有针对非仿射制导策略的设计成果,因此,文中所提的制导方法可以适用于更加复杂的制导系统。

2) 实际制导过程中目标机动信息往往未知且难以测量,文中所设计的制导策略不依赖目标机动信息,无需额外引入观测器等测量工具,降低了制导律设计的复杂性。

1 问题描述与控制策略设计

考虑如下非仿射非线性系统

(1)

由于系统对控制输入表现为非仿射形式,使得控制器设计变得困难,则考虑控制补偿技术[20],构建如下辅助系统:

(2)

其中:M(u)∈Rn、G(u)∈Rmxp为已知函数,且G(u)为有界函数;μ∈Rp为辅助控制输入。

定义新状态z=[xT,uT]T,则式(2)变为如下增广系统:

(3)

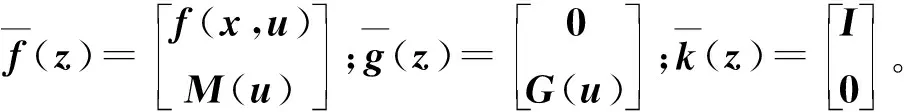
考虑如下博弈型性能指标[16]

(4)

其中:Q(z)为关于z的二次型函数;R1,R2为正定对称矩阵。定义哈密顿函数为:

(5)

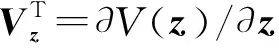
基于Nash-Pontryagin极大极小值原理,纳什均衡解(μ*,ω*)使得最优性能指标满足:

(6)

则推导出微分对策最优控制对为:

(7)

将式(7)代入式(6)可得相应的HJI方程:

(8)

构建如下神经网络逼近性能指标,在线求解HJI式(8)的解:

V(z)=WTθ(z)+Δ

(9)

其中:W∈RL表示理想神经网络权值向量;θ(z)∈RL表示激励函数;Δ表示逼近误差。

相应的最优性能指标偏导数:

(10)

其中:θz=∂θ(z)/∂z;Δz=∂Δ/∂z表示相应函数对z的偏导数,代入式(7)得最优微分对策控制为:

(11)

(12)

其中神经网络近似误差为:

(13)

利用神经网络输出值,得近似性能指标

(14)

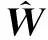
(15)

则神经网络权值误差为:

(16)

则近似最优微分对策控制器表达式为:

(17)

近似哈密顿函数表达式为:

(18)

为了设计权值更新律,首先定义如下积分二次型目标函数:

(19)

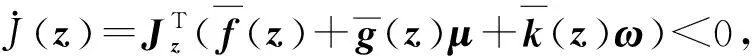
(20)

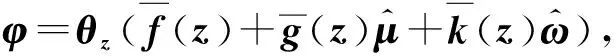
(21)

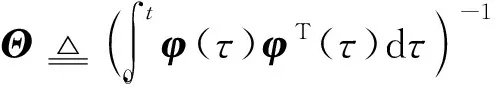
(22)

(23)

选择Lyapunov函数:

(24)

首先,求导第一项V*(z)可得:

(25)

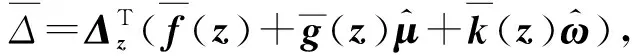
接着,考虑第二项J(z),求导可得

(26)

对第三项求导可得:

(27)

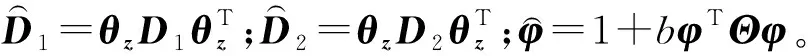
观察式(27)可以发现,由于开关函数Γ的存在,结合式(23),系统分两种情况讨论:

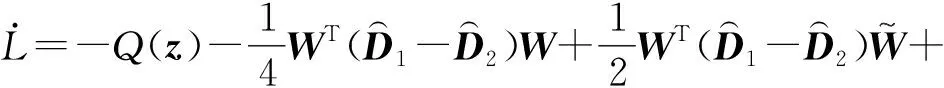
(28)

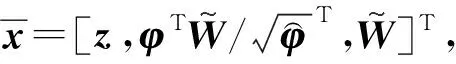
(29)

(30)

(31)

2)Γ=1此时学习网络不稳定,则可得:

(32)

基于假设,容易得到D1-D2也是有界的,令其界为ψ,则有:

(33)

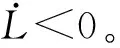
由式(33)可知,下列不等式满足其一:

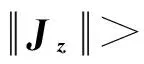
(34)

(35)

2 仿真验证

2.1 导弹拦截系统模型

为了验证所提算法的有效性, 文中将设计的最优控制器应用于导弹拦截制导系统的末制导阶段中,考虑如图1所示导弹拦截系统。

图1 导弹拦截系统Fig.1 Missile interception system

(36)

并且,导弹与目标自动驾驶仪系统均为一阶系统,且其质心方程表达为:

(37)

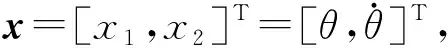
(38)

根据控制补偿技术(2),构建如下辅助系统:

u=-2u+0.2μ

(39)

。

仿真目标为设计μ使得导弹能够成功拦截目标。然而,观察式(38)可以发现,当r→0,此时系统被破坏。因此,存在一个最小距离参数rm,即脱靶量,使得当r≤rm时,制导结束,剩余拦截任务依靠惯性完成,且需满足目标拦截必要条件:

(40)

2.2 参数设定与仿真结果分析

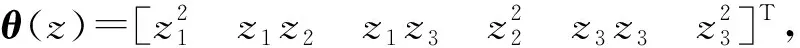
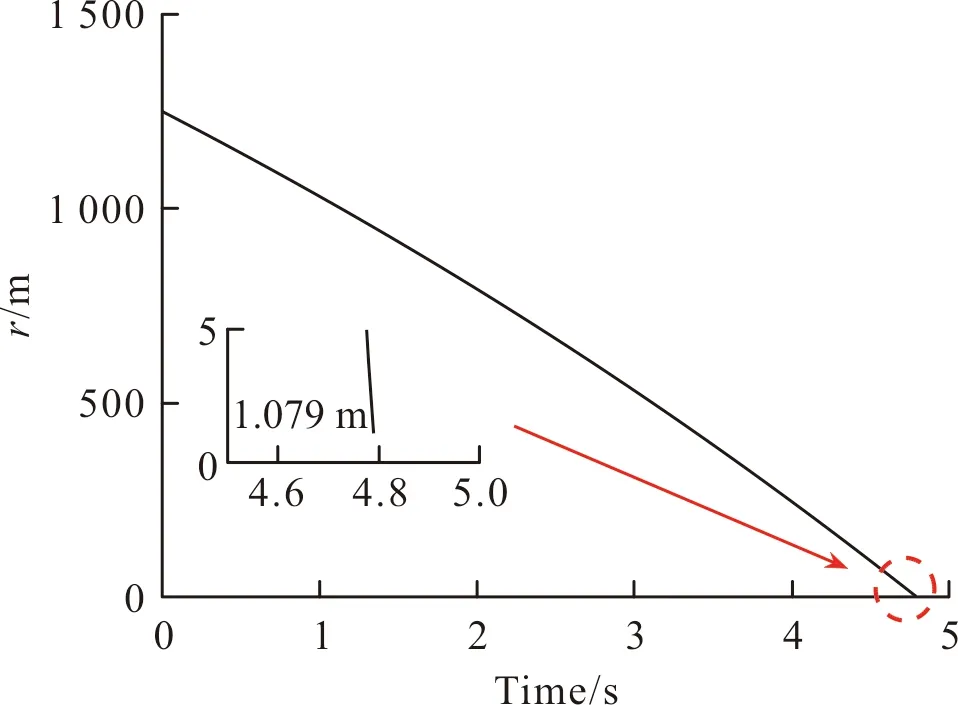
图2 相对距离Fig.2 Relative distance

图3 导弹-目标拦截轨迹Fig.3 Missile-target intercept trajectory

图4 视线角速率Fig.4 The line of sight angle rate

图5 相对速率Fig.5 Range rate

图6为权值泛数曲线图,可以看出,在积分权值更新律式(21)作用下,权值估计误差有界,并且可以发现,权值曲线在很短的时间内即趋于稳定,表明神经网络学习时间相较于制导时间是很短的,则对于制导过程的实时性影响较小,因此 可以实现控制器式(17)更好的在线学习。观察图2～图6可以发现,在制导的最后阶段,曲线均呈现出发散特性,这主要是由制导动力学模型的特点导致的,根据式(38),当导弹与目标足够接近时,即r→0,则系统动态区域无穷大,导致状态发散,此时制导律将不再适用。因此出现发散现象是必然的。

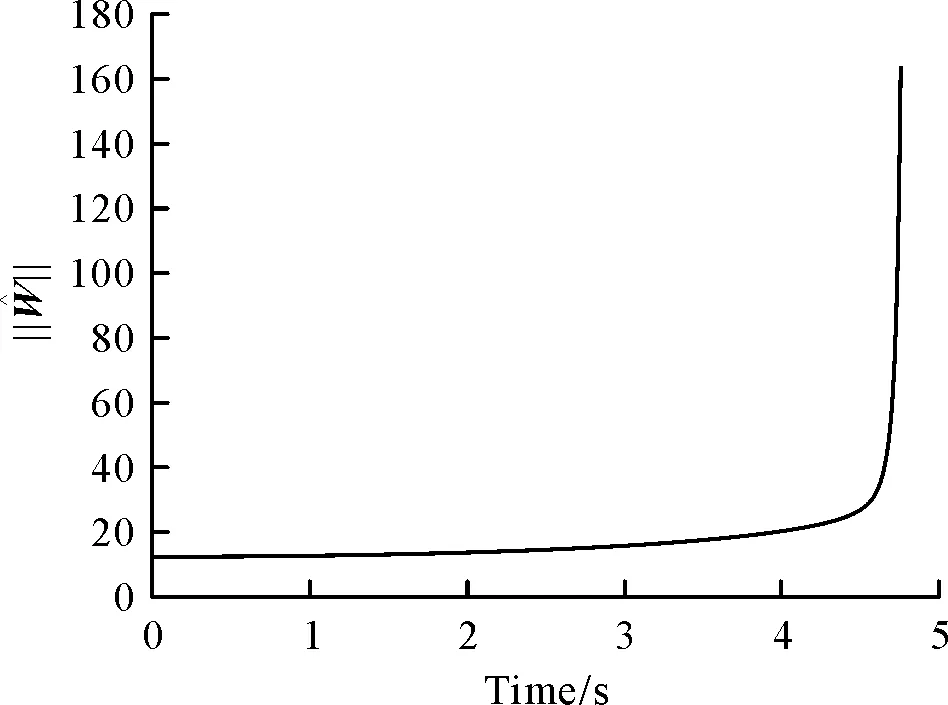
图6 权值泛数Fig.6 Norm of weight

3 结论

为解决目标机动未知和存在控制非线性项的导弹拦截系统制导问题,研究了非仿射导弹拦截系统的制导律设计问题。利用控制补偿技术处理非仿射控制输入。进而,将目标机动视为未知扰动,结合微分对策理论,给出目标机动最坏情况下的制导策略设计方案,实现制导过程的稳定性并满足最优性能指标, 引入积分自适应动态规划技术, 利用神经网络设计一类新的积分权值更新律, 在线学习微分对策最优制导策略,实现对机动目标的成功拦截。并保证整个闭环制导系统最终一致有界。与传统制导策略相比,克服了因控制非线性项的存在从而导致制导策略解析形式无法获得的问题,并且降低了对目标机动信息的依赖,无需额外引入观测工具,减少了制导策略设计的复杂程度。然而,在制导的过程中受战场环境的影响,外部扰动、信息传输延迟问题总是不可避免,针对非仿射导弹拦截系统的鲁棒控制和时滞问题将在之后的研究中进一步讨论。