“细说”圆锥曲线的弦长公式

广东省韶关市广东北江中学(512026) 罗贤

圆锥曲线为C:f(x,y)=0(可以是椭圆, 双曲线, 抛物线),设直线l:y=kx+m(特殊情况要讨论斜率k不存在的情况),联立方程组消y得关于x的一元二次方程为

它的判别式为Δx=B2- 4AC, 当Δ＞0 时, 直线l与曲线C有两个交点, 分别设为P(x1,y1)Q(x2,y2),则坐标x1,x2为方程①的两个实根, 可用韦达定理:, 点P,Q在直线上, 故有y1=kx1+m,y2=kx2+m⇒y1-y2=k(x1-x2).

带入韦达定理可得:

我们把这个公式叫做“万能弦长公式”.

如图所示的折纸也称“工艺折纸”,是一种把纸折成各种不同形状物品的艺术活动, 在我国源远流长某些折纸活动蕴含丰富的教学活动. 某些折纸活动蕴含丰富的数学内容,例如,用圆形的纸片按如下步骤折纸:

步骤1: 设圆心是O,在圆内(除去圆心)取一点,标记为F;

步骤2: 把纸片折叠,使圆周正好通过F;

步骤3: 把纸片展开,于是就留下一条折痕;

步骤4: 不停的重复步骤2 和3,能得到越来越多的折痕.这些折痕围成的图形是一个椭圆;

若取半径为4 的圆形纸片,设定点F到圆心O的距离为2,按上述方法折纸,如图1;

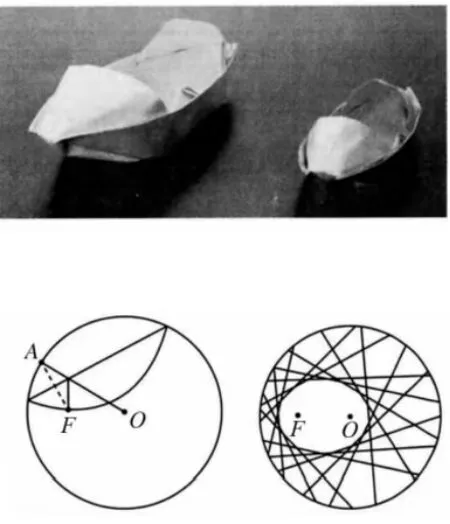
图1

(1)以FO所在直线为x轴,FO中点M为原点,建立平面直角坐标系,求折痕围成的椭圆的标准方程;

(2)求经过点F,且与直线FO夹角为的直线交椭圆于C,D两点,求ΔOCD的面积.

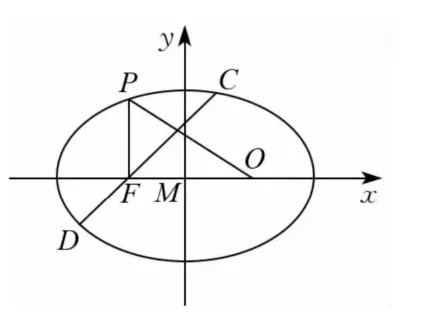
从解题中我们可以窥见弦长公式的本质有两个:

一是韦达定理的应用,即关于x的一元二次方程为

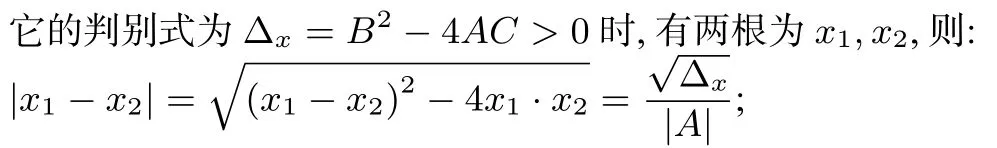
突破了此难点2022 新高I 卷21 题,无论是运算还是思维都没有难点了;这里是新增加的一点看法,请老师审核这个解法在得到韦达定理乘法结论式具有强大的优势,但是得不到加法式的结论;

(2021 浙江高考21) 如图, 已知F是抛物线y2= 2px(p＞0)的焦点,M是抛物线的准线与x轴的交点,且|MF|=2,

(1)求抛物线的方程;y2=4x

(2) 设过点F的直线交抛物线与A,B两点, 斜率为2 的直线l与直线MA,MB,AB,x轴依次交于点P,Q,R,N, 且|RN|2=|PN|·|QN|,求直线l在x轴上截距的范围.

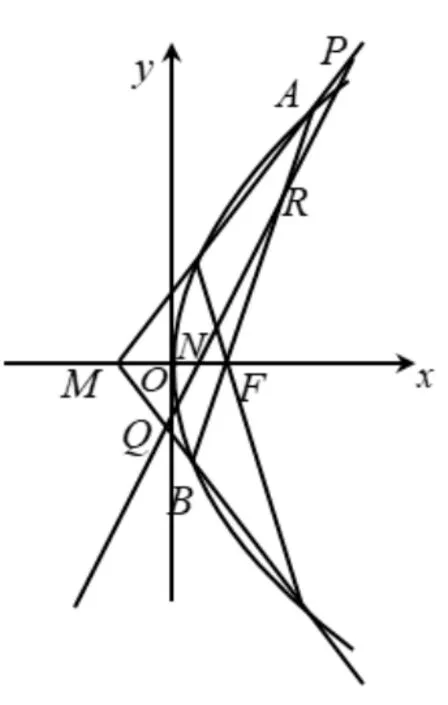
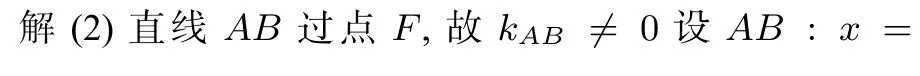
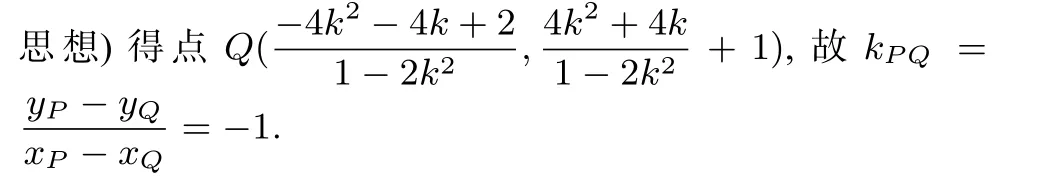
通过研究高考题我们发现,以前的高考着重于公式的应用,多以椭圆为载体考查学生对公式的掌握和应用情况. 对比近两年的新高题,弦长公式从椭圆转到到双曲线、抛物线,从直接使用韦达定理转化到解题关键是先使用距离公式;不管怎么变,万变不离其宗,理解知识的根本,抓住解决问题的关键,才能到达核心点,达到用一个知识点解决一类问题的目的,比如弦长公式的本质首先是直线上两点之间的距离公式,其次才是使用韦达定理. 尤其是2021 新高考第21 题,虽然这个题有很多种解法,我的体会是这个题的出发点在弦长公式的本质的理解,基于这种理解在解决2022 新高卷题11和题21 时就很得心应手,不觉它是难题了. 2022 新高考题21(2)问,我们还应该有这样的理解,学了正弦定理以后,正弦表示三角形面积公式比初中所学的三角形面积公式高级,在已知角度的情况下,该选择高中的公式求面积,后面的思路就顺其自然.