基于局部寻优的噪声特征线谱智能识别算法研究

杜德锋，何江贤，孟凡凯

(1.91388部队45分队，广东湛江 524002；2.海军工程大学，湖北武汉 430033)

0 引 言

复杂旋转机械系统中的设备加装隔振装置后，在振动信号低频段中仍表现出突出的特征线谱[1]。这些特征线谱通过船舶壳体传到水中，形成辐射噪声，对船舶隐身性能造成了危害。为降低船舶的振动噪声水平，应准确定位振源，阻断振动传递路径，减小振动对船舶壳体的冲击。系统各测点的特征线谱间的耦合关系反映了振动的传递路径，特征线谱的智能识别对于快速找到各测点特征线谱的耦合关系具有重要意义。

在旋转机械振动特性分析过程中，常采用功率谱法分析特征线谱进而判断设备状态。目前应用较广泛的方法有：(1) 通过小波阈值方法对信号进行降噪处理，根据奇异性分析结果提取线谱[2]。(2) 采用自适应线谱增强器，在线谱识别和筛选过程中增强线谱，抑制宽带干扰[3]。(3) 人工对线谱进行识别提取。上述方法主要侧重于抑制噪声，提高信噪比，使线谱特征在功率谱信号中更加明显，因而存在计算误差大、运算效率低、测点布放受限等缺点，有的方法还需要特征频谱的先验知识[3-5]。

为解决机械系统复杂运行工况下的特征线谱提取问题，以最小二乘法拟合的趋势项为准零线将功率谱分为上下两部分，对于零线上的不连续谱线进行分组，对每组线谱簇进行局部寻优初步获取特征线谱，并按照谱线权重排序，得到准确有效的特征线谱序列。经过验证，该方法运算速度快，提取结果准确可靠，可实现指定频段特征线谱的快速提取。

1 特征线谱的理论模型

由于机械运动件的几何轴线不对中、质量不平衡、轴颈轴承间隙过大等因素引起机械的强迫振动，其中包括周期振动、冲击振动、随机振动[6]，因此振动功率谱由连续的谱和大量周期性特征频率叠加而成[7-8]。连续谱可以用宽带平稳随机过程拟合，因此振动噪声可表示为

式中：{x(t)}表示为宽带平稳随机过程，li(t)表示为相位随机的周期信号。

振动功率谱可表示为

式中：T为做傅里叶变换时参与运算的每段信号的长度，E 为求集合平均，K为信号段编号[8-9]，SK，T(f)代表第K段的长度为T的样本序列x(t)对应的功率谱密度。通过对每段信号的功率谱求平均得到该信号的功率谱估计，该方法能够克服直接法中由于数据长度T过大引起的谱曲线起伏加剧、T太小导致分辨率下降的问题。

周期信号li(t)带来的特征频率是一系列线谱。特征线谱一般包含主峰和旁瓣，在特征线谱附近的频域范围内，特征线谱的幅度最大，在特征线谱两侧幅度呈递减趋势。特征线谱幅度相对于附近频域的幅度均值应高出6 dB。

2 基于局部寻优的特征线谱识别

功率谱可视为连续谱与特征线谱的叠加。因此特征线谱识别前应分解功率谱，获得无连续谱数据干扰的特征线谱数据基底。根据最小二乘法原理拟合出连续谱(如图1(a)所示)，以连续谱为准零线将功率谱分为上下两部分，并把零线上具有非连续特点的特征线谱数据基底分组(如图1(b)所示)，对各组数据进行局部分析。特征频谱在各分组中会表现出凸起的特点，因此只需找出局部最大值且满足6 dB 信噪比的线谱，就识别出了该组的特征线谱。

图1 去除连续谱后功率谱经“0”“1”映射的分组Fig.1 Power spectrum grouping mapped with “0” and “1” after removal of continuous spectrum

功率谱的线谱频率记为xi(i=1，2，…n)，功率用振动加速度来表征，记为yi(i=1，2，…n)。功率谱趋势项可准确反映计算频段内系统幅频特性变化趋势，为兼顾收敛速度及精度，采用多项式拟合趋势项yFi：

本文主要探讨如何将区块链技术应用到高校在线阅读服务领域，并从区块链技术理论入手，在互联网技术下，通过区块链在安全开放共享方面的特性来实现高校联盟模式下的在线阅读互动平台。

式中：K为多项式的最高次幂，am为多项式系数。am可基于最小二乘法原理获得，进而获得拟合趋势项yFi。

最小二乘法就是以残差的平方和最小为拟合准则，寻找最优逼近曲线[9-10]，即：

为满足ϕ的极小值要求，逐个对am求偏导：

设其偏导值为0，得到K+1个线性方程组:

通过求解式(6)中方程组，进而求得拟合多项式系数am及拟合值yF。

以趋势项为基准将初始功率划分为零上部分和零下部分，得到非连续特征线谱数据簇，划分方程为

式中：YFi代表去除趋势项后的新的功率谱值。通过判断零上或零下实现功率谱序列“0”“1”映射。

为了获取所关心频率区间首、尾处可能存在的特征线谱，需要在首、尾外侧补“0”，使得所有可能出现特征线谱的数据都能被分组而不被遗漏。

有效特征线谱取值索引方程为

式中：XOR(·)表示异或。通过式(10)、(11)判断连续“1”区间的起始索引和结束索引，将零上部分化为多组连续“1”区间，对每组“1”区间对应的功率谱进行局部寻优得到该段的特征线谱。

式(10)、(11)分别描述了区间段的起始条件、结束条件。对于“0”“1”排布序列，当相邻两元素不同，且后面元素值为1时，则后面元素为频率提取区间的起始点；当相邻两元素不同，且后面元素为0 时，则前面元素为频域提取区间的结束点。通过式(10)、(11)可将特征线谱段所在区间提取出来，从而进一步提取出特征线谱。线谱提取算法流程图如图2所示。

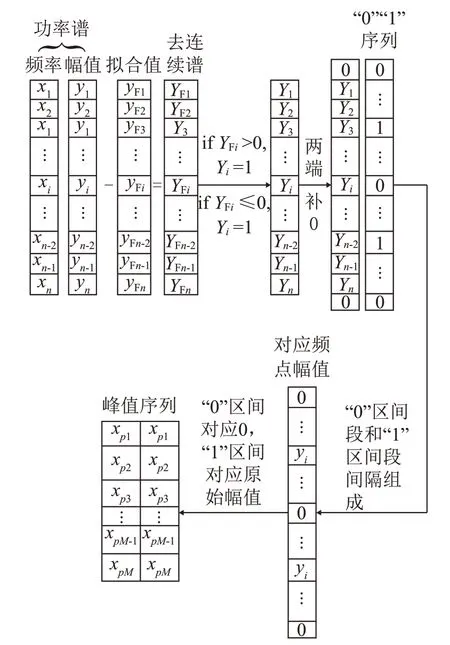
图2 局部分组寻优提取特征线谱流程图Fig.2 Flowchart of feature line spectrum extraction by local group optimization

原始功率谱经趋势项划分后形成N组区间(自然数序列编号)，第k组区间需要根据局部信噪比来辨别局部最大值是否为特征频率，若是则编号为第k'(k'≤k)个特征线谱，若不是直接跳过对下一组进行识别，最终共形成M个峰值，并按照以下四种方式分配权重并排序：(1) 根据峰值绝对大小进行从大到小的权重排序；(2) 根据特征线谱的峰值与附近线谱均值的比值大小进行从大到小的权重排序；(3) 对关注的某个频段范围内的峰值进行权重排序；(4)根据对应功率谱幅值的方差进行从大到小的权重排序。最终得到特征线谱峰值及频率序列，根据需要取前M'(M'＜M)个特征线谱进行后续分析。

3 算法验证

3.1 算法识别试验

为验证算法的有效性，利用在船用阀控型舵机故障测试过程中(如图3(a)所示)所采集的左柱塞缸测点振动数据进行验证测试。左柱塞缸振动时域波形如图3(b)所示，功率谱如图4(a)所示。通过局部寻优(多项式拟合K取9)所得到的功率谱趋势项如图4(b)所示；得到的非连续特征线谱数据簇如图4(c)所示；根据算法最终得到的特征线谱峰值序列如图4(d)和表1所示。

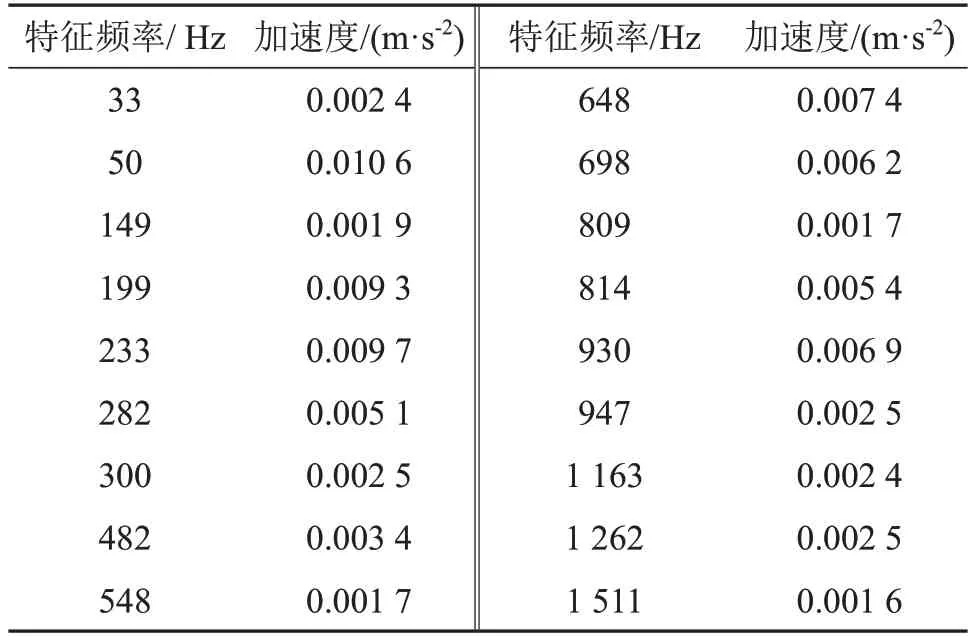
表1 基于局部寻优的特征线谱提取应用Table 1 Application of feature line spectrum extraction based on local optimization

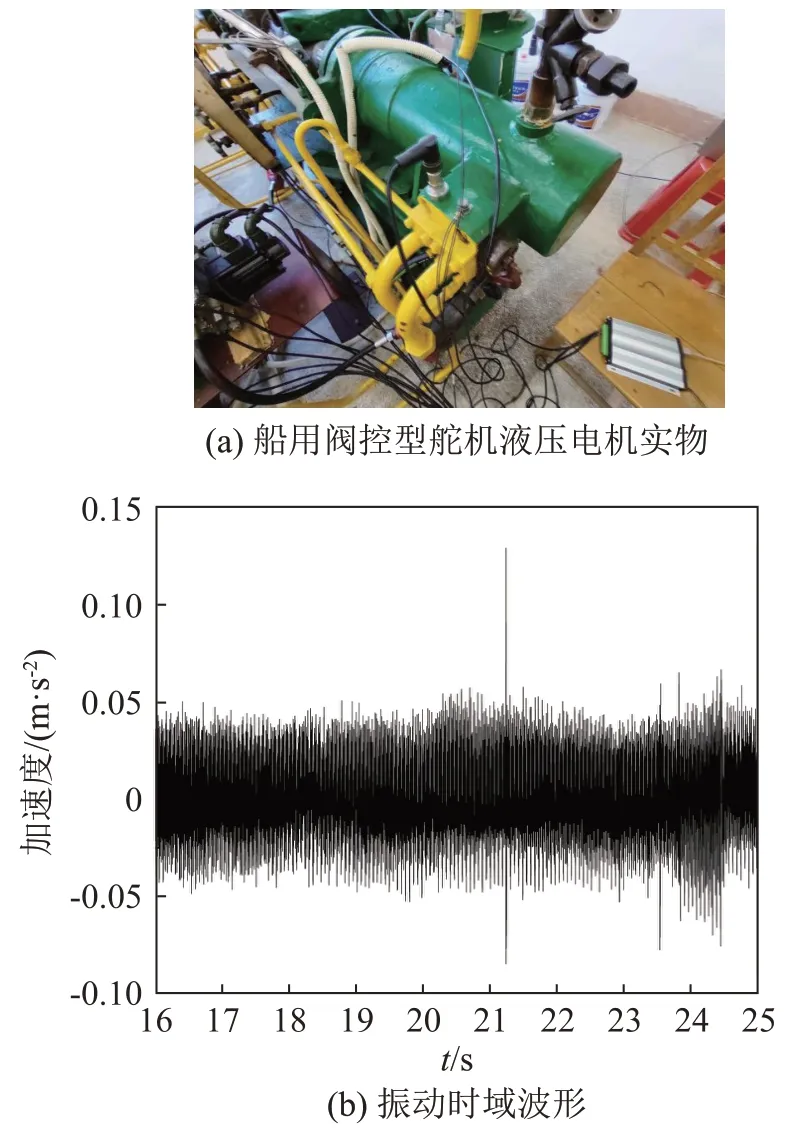
图3 阀控型舵机液压电机实物及其振动时域波形Fig.3 The actual hydraulic motor of valve-controlled steering gear and its time-domain waveform

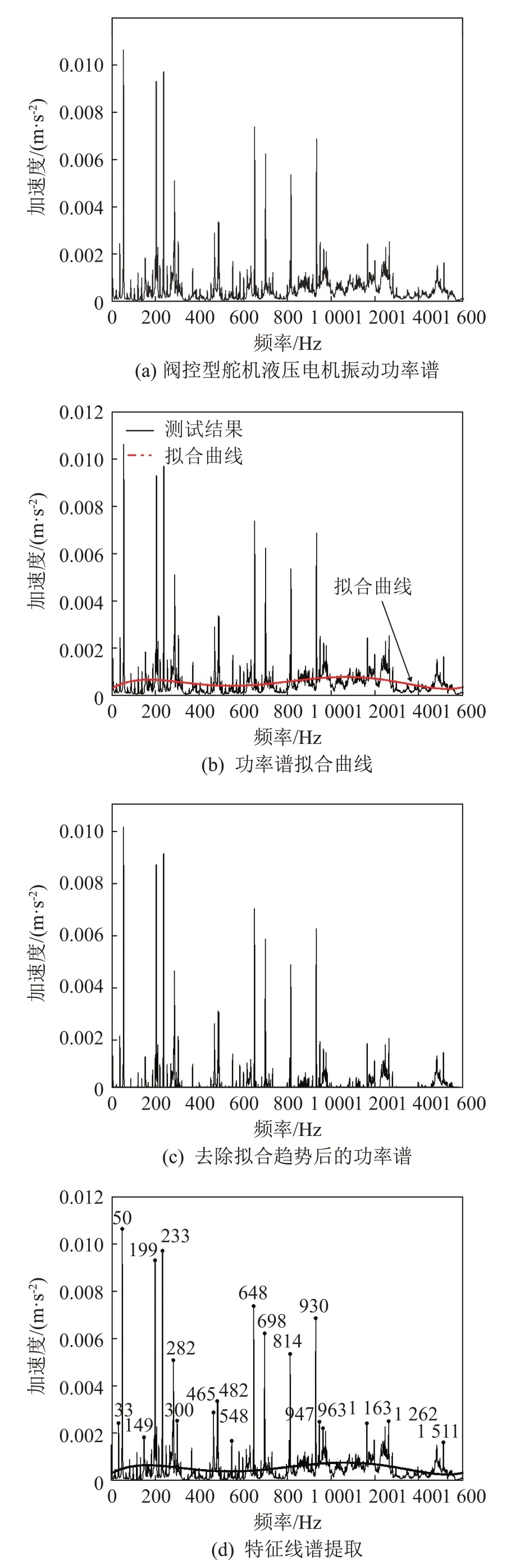
图4 局部寻优特征线谱提取过程Fig.4 Process of extracting characteristic line spectrum by local optimization method

3.2 算法识别与人工识别差距

由图4(d)可知，算法识别的特征线谱准确度较高。在低频段，仅有较为明显的365 Hz 和主特征线谱附近的密集小特征线谱未能检测出，其余主要的大特征谱都能检测出来。算法精度方面，该算法曾广泛运用到大型船舶振动测试分析中，识别了上万条数据的特征线谱，能够提取出机械设备的典型谱线特征，并且能够筛选出机械设备的梳状谱。将该算法推广到水中辐射噪声特征线谱的提取，识别精度高，只有个别密集小线谱漏检。

3.3 最小二乘法中拟合多项式最高次幂对识别精度的影响

当最小二乘法中拟合多项式最高次幂K分别取5、6、7、8、9、10时，功率谱(0～1 600 Hz)中特征频率个数分别为19、19、18、18、18、18，所识别的特征频率重复率很高，如图5(a)所示，图中圆圈代表识别到的特征频率。将这6组所有特征线谱集合后去掉重复的20个线谱，做比较基准，K不同时识别的特征线谱个数在基准个数中的占比就是漏检率，漏检率是一个相对概念，是用来评判最小二乘多项式最高次幂K的选择对特征线谱识别结果的影响。漏检频谱集中出现在密集线谱处，如图5(b)所示。以上6 组数据得到的漏检率具体如表2 所示，统计频率范围为1～1 000 Hz。可以看出并不是最高次幂越高越好。当K=5时，由于趋势项变化较更高次幂更为平坦，809 Hz 处的线谱与附近814 Hz 处的特征线谱靠得太近，被划分为同一组而出现漏检；当K为6～10 时，在频率465 Hz 与482 Hz 处，因最高次幂偏高，趋势项在此处发生了畸变，导致这两组频率被划分在一组。因此多项式拟合最高次幂K取5即可。多项式最高幂次对局部寻优影响不大，取大了对于整体挑选影响不大，还可能出现个别频点漏检。

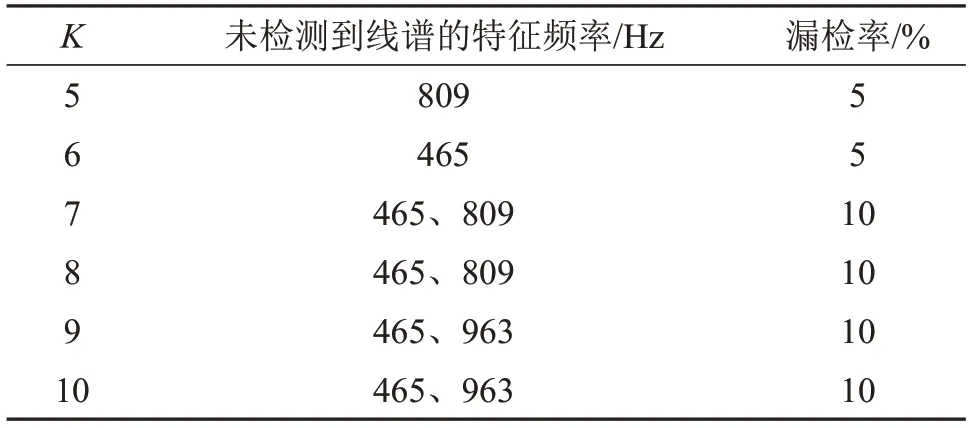
表2 多项式最高次幂对识别精度的影响Table 2 Influence of the highest power of the polynomial on recognition accuracy

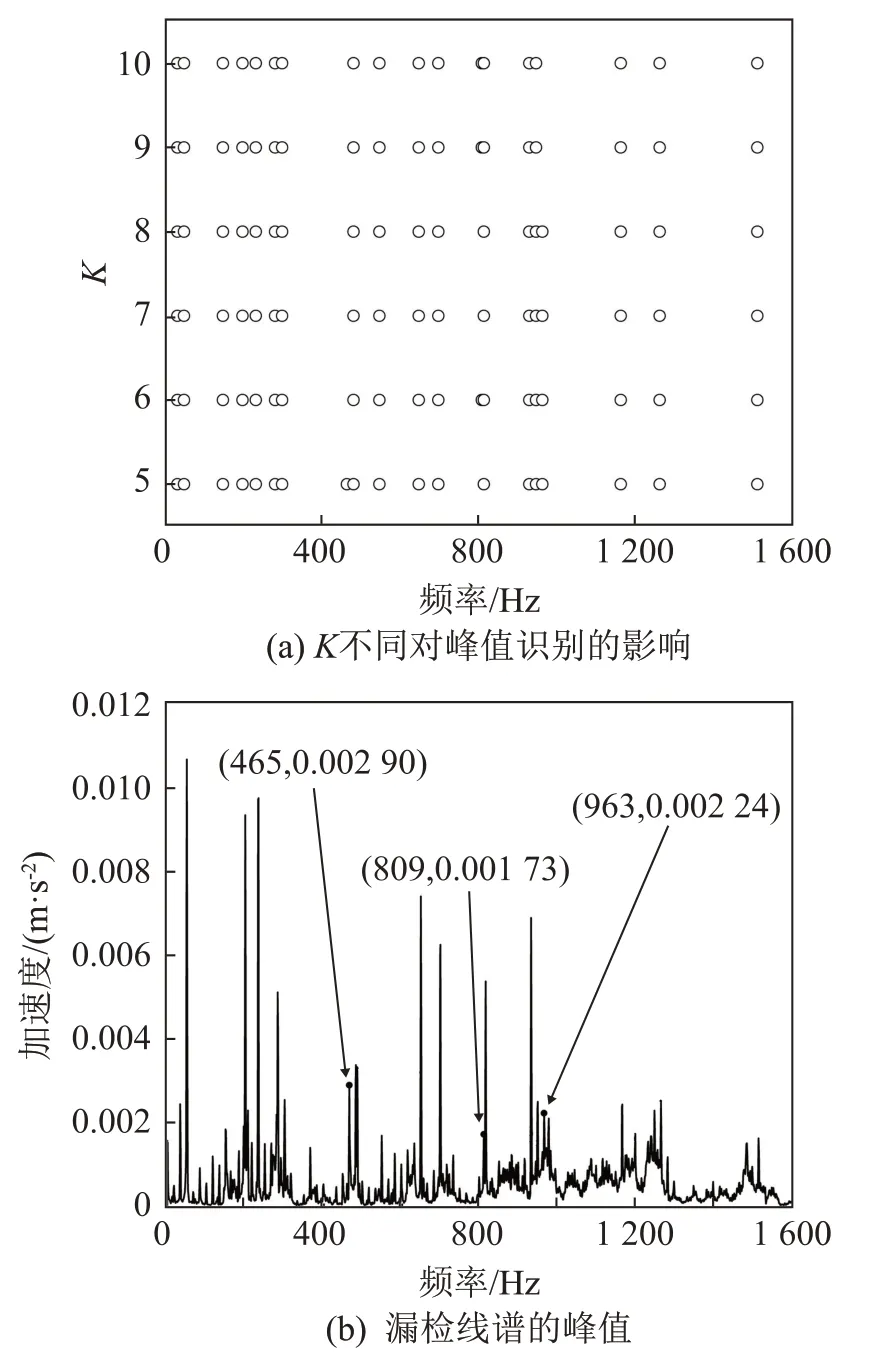
图5 多项式最高次幂对峰值挑选的影响Fig.5 Influence of the highest power of the polynomial on peak selection

4 结 论

本文主要研究旋转机械振动特征线谱的识别及筛选问题，给出一种基于最小二乘法分组局部寻优的提取算法，该方法能够有效识别筛选低频段的特征频率，并通过试验验证了算法的兼容性和有效性，具有一定的工程实践应用价值。