路噪结构载荷模拟方法研究

肖文浩，朱亚伟，卢炽华，刘志恩

(1.武汉理工大学现代汽车零部件技术湖北省重点实验室，湖北武汉 430070；2.汽车零部件技术湖北省协同创新中心，湖北武汉 430070；3.佛山仙湖实验室，广东佛山 528200)

0 引 言

随着汽车工业的发展，汽车的噪声、振动与声振粗糙度(Noise、Vibration、Harshness,NVH)性能作为驾驶舒适性的核心指标，成为用户购买汽车的重要考虑因素[1-2]。新能源汽车失去发动机噪声的掩蔽，路面噪声(简称：路噪)问题更加凸显，关于路噪的分析，一般相对复杂，通常采用传递路径分析法(Transfer Path Analysis,TPA)将路噪分解为空气传播噪声与结构传播噪声[3]。空气传播噪声主要为轮胎与路面相互作用，以及轮胎自激振动发出的噪声，空气噪声的频率一般大于500 Hz[4]。这部分噪声一般采用汽车声学包解决。但是面对不同车型，结构路噪的贡献一般没有确切的范围。Avutapalli等[5]在处理一辆SUV的路噪问题中发现结构噪声主要贡献频率在400 Hz以下；赵伟丰等[6]将路噪按频率分为不同区间，认为结构路噪主要作用区间在率频400 Hz以下；Bartolozzi等[7]在模拟整车路噪时关注的结构路噪频率范围为50～350 Hz；房旭[8]在其研究的路面噪声OTPA模型中，所取的最大代表性频率为356 Hz；肖忠等[9]针对纯电动车低频路面噪声问题时，重点分析200 Hz 以下的主要峰值；夏洪兵[10]在研究某SUV的低频路面噪声时，认为低频路面噪声通过结构传播至车内的噪声频率一般低于300 Hz。综上可以发现，路面噪声结构传播噪声导致的汽车NVH问题，频率一般在400 Hz以下。

路面噪声结构传播噪声由车轮经悬架系统传至车身，引起车内人员不适[7,11]。为分析车辆的路面噪声结构传播噪声，通常要求试验车上路实测或者用转鼓模拟路面工况。Roozen 等[12]依托齿轮箱试验，提出了一种新的利用外部激励来测量传递率的方法，在大多数情况下采用此方法测得的传递率质量高于运行工况下的结果，原因是采用外力激励时，其响应很大程度上相互独立，而运行工况下的响应信号通常是相关的。

引入外部的激振力对系统进行激励，然后测试参考点到目标点之间的传递率，为响应-响应型TPA的改进研究提供了一种新思路。为分析路面噪声结构传播噪声，针对激励源同时作用的问题，本文提出以一个试验台为依托研究路噪结构载荷的模拟方法，根据式(1)求得传递率矩阵T，再将模拟工况与实际运行工况求得的T作对比，验证所提出方法的可靠性[13]。

式中：GYX为响应与参考点响应的互谱，GXX为参考点响应的自谱。

1 响应-响应型TPA传递率求解

所研究方法属于响应-响应型TPA，响应-响应型TPA模型，一般可以表示为[13]

式中：y(ω)为接收位置的目标响应信号，ai(ω)为结构载荷的参考响应信号，pi(ω)为声载荷的参考响应信号；Ti(ω)、Tj(ω)为参考点与目标点之间的传递率，为目标响应和参考响应信号的互谱与参考响应信号自谱之比；m为结构载荷参考点个数，n为所有载荷参考点总个数，n-m即为声载荷的参考点个数。

将式(2)写成矩阵形式为

式中：k为工况的总数；yk表示第k个工况的目标响应信号；akm表示第k个工况、第m个结构载荷的参考响应信号；pkn表示第k个工况、第n个声载荷的参考响应信号；Tn表示第n个参考点到目标点的传递率。

为求解传递率矩阵T，将式(3)进行矩阵变换，可得：

现设X为参考响应信号矩阵，Y为目标响应信号矩阵，则传递率矩阵T可表示为

当独立工况的数量足够多，X为列满秩矩阵时，X的逆矩阵可以表示为

式中：上标H表示共轭矩阵。

联立式(5)和式(6)，可得：

式中：XHX=GXX，XHY=GYX。实验时不可避免地存在各类干扰噪声，通过对不同工况信号的自谱和互谱进行平均来实现降噪。

当各路径的参考响应信号之间存在强相关时，GXX为病态矩阵。通常先对矩阵GXX进行奇异值分解，即：

式中：U(k×k)和V(k×k)为正交矩阵，U(k×k)由矩阵GXXGHXX的k个特征值和对应的k个特征向量u构成；V(n×n)由矩阵GHXXGXX的n个特征值和对应的n个特征向量v构成；∑(k×n)除了主对角线上是奇异值σ其他位置都是0，其中σi=i≤n。则GXX的广义逆矩阵为

式中：上标+表示矩阵的广义逆。

一般响应-响应型TPA 法的关键是获得参考点到目标点的传递率矩阵，核心在于求解参考响应信号自谱矩阵的逆矩阵，在GXX为病态矩阵时，虽然通过奇异值分解可以求得其伪逆解，但是结果存在较大的随机性，难以保证传递率求解的精度[14]。因此，在建立TPA模型时，应尽可能采用不同工况下的数据，保证不相关的工况数量大于传递率的数量，以改善奇异值分解时矩阵的条件数[15]。由式(2)～(7)可知，在参考响应点和目标响应点位置确定的情况下，它们之间的传递率只与激励源的位置有关，而与激励源的强度无关，理论上说明用激振器模拟路噪结构载荷具有可行性。同时用激振器作为激励源得到的响应很大程度上相互独立，因此可以在较少的工况数据中获得参考响应信号的列满秩矩阵，进而求解传递率矩阵。

2 实验方案设计及试验台开发

2.1 方案设计

使用微型激振器为车辆提供外部激励，为真实模拟路面对车轮的激励，激励点应为车轮与地面的接触处，故在试验台的上台面设有3个安装孔，实现激振器在车胎底部的安装。3个激振器均匀布置在车胎上，使激励更加接近真实路况。同时试验台模拟的是地面对车辆的支撑，由于实际试验台的刚度不可能无限大，因此要实现试验台对地面支承的模拟，要求试验台的最低弹性频率高于400 Hz。因为路面噪声结构传播噪声导致的汽车NVH 问题，频率一般在400 Hz 以下，试验台的最低弹性频率高于400 Hz 可以避免在关注频率范围内，试验台被激励从而导致分析误差。路噪结构载荷模拟方案示意图如图1所示。

图1 路噪结构载荷模拟方案示意图Fig.1 Simulation scheme of road noise structural load

2.2 试验台结构设计及材料选择

家用车胎宽度一般为165～225 mm[16]。考虑使用误差，将上台面尺寸定为320 mm×250 mm。微型激振器高度一般在60 mm以内，再综合考虑板材厚度、结构刚度、安装激振器时的操作空间，将设备整体高度定为124 mm。

为了适应常见的165～225 mm车胎宽度，方便微型激振器的安装，避免激振器工作时与台面干涉，应尽可能地增大安装孔的直径。但是孔的直径过大又会导致轮胎与设备的接触面减小，轮胎局部压强过大，产生较大的变形，不符合真实的轮胎使用场景。综合考虑上述因素，将安装孔的直径定为58 mm，相邻两孔之间的距离为70 mm，安装孔开设在上台面的中心位置。综上，确定试验台整体尺寸为320 mm×250 mm×124 mm，试验台示意图如图2所示。

对于试验台的加工，焊接比整体铣削加工更具有经济性，也可保证较高的连接强度及连接刚度，故试验台采用焊接加工。为保证z向的支撑强度，采用上下台面钢板夹住中间三个支撑板的布局。考虑到试验台的使用场景，不存在摩擦及转动等情况，为一般使用要求，选定材料为钢Q235-A。钢Q235-A 广泛地用于一般要求零件和焊接结构[17]，符合本试验台对钢材的要求。

机械分析中，结构模态的频率与模态刚度及模态质量间的关系为

式中：ω为结构模态频率，k为结构模态刚度，m为结构模态质量。

为保证试验台具有较高的一阶弹性模态(以下模态未作说明均指弹性模态)，由式(10)可知，试验台的刚度应越大越好。材料力学中，将各类刚度表示为弹性模量与相应截面几何特征的乘积，在材料确定时，截面几何特征又决定着质量[18]。本试验台基本结构及材料已确定，为增大刚度只能从焊接工艺以及钢材厚度着手处理，考虑试验台的轻便性，确定钢材厚度为12 mm。

2.3 试验台模型

利用SolidWorks 软件对试验台进行三维建模后，在HyperWorks 进行网格划分与建立约束。建立约束时，考虑试验台的美观性，只对其内部还有开口处进行了焊接处理。焊接处理示意图如图3所示，图中箭头指向的黑色位置为焊缝。如果该焊接处理无法使试验台的一阶模态频率大于400 Hz，可以通过在试验台外部增加焊点或者加厚板材厚度来增大其一阶模态频率。考虑后续试验验证，会有加速度传感器的附加质量影响，尽管试验台自身质量较大，但参与模态的并不是结构的全部质量，而是结构模态上活跃部分的有效质量[19]。故在有限元分析时，对传感器布点进行附加质量补偿，评估传感器附加质量对试验台模态频率的影响。传感器附加质量在图3中用黄色网格表示。

依托建立的试验台有限元模型，以是否进行传感器附加质量补偿为控制变量，进行两组自由模态分析，分析结果如表1表示。

表1 传感器附加质量补偿前后计算的模态频率Table 1 Mode frequencies calculated before and after adding the additional mass to the sensor

对比传感器附加质量补偿前后的计算模态，发现前三阶模态频率的变化量均小于0.3 Hz，可忽略传感器附加质量对试验台模态频率的影响。从仿真结果来看，一阶模态频率与400 Hz 的关注频率约有35 Hz的裕度，可安排加工。加工时应考虑机床加工误差与装配误差，在加工图纸上清晰标注各形状公差和位置公差。各阶计算模态振型如图4所示。

图4 计算模态的一至三阶振型Fig.4 The 1st to 3rd mode shapes in the calculated modes

2.4 锤击测试

测试在整车半消声室进行，实验室的截止频率为63 Hz，本底噪声为18.0 dB(A)。测试分为两步进行：(1) 按照有限元分析时传感器既定布点进行加速度传感器布置；(2) 分别使用气柱卷和空气海绵模拟自由边界，进行两组锤击试验，测量试验台的模态频率。测试设备如表2所示，测试场景如图5所示。

表2 测试设备Table 2 Testing facilities

图5 气柱卷与海绵分别模拟自由边界Fig.5 The free boundaries separately simulated by air column and sponge

有限元分析结果表明，试验台关注的低阶模态，模态振幅最大区域位于A6、A7、A8三点，A6和A8为对称点。理论上在模态振幅较大的区域锤击，比较容易激励起该阶模态，故锤击点定为A6、A7两点。考虑本试验台只关注低阶模态频率，尤其是第一阶模态频率，有限元分析得到的第一阶模态频率为435.31 Hz，因此根据采样定理将采样频率设置为1 024 Hz。

以A6、A7分别作为激励点，13个加速度传感器布点为模态参考点，各锤击5次，结果取5次结果的平均值。测试结果如图6所示。

测试结果表明两种模拟自由边界的方法得到的模态频率略有差异，频率差值均在1 Hz 以内。相对于海绵模拟边界，气柱卷模拟边界条件时，在更小的拟合多项式数量(Model size)就可以稳定，且一致性更好，故选用气柱卷为边界条件时测得的模态数据，前三阶模态频率分别为：435.38、535.17和838.43 Hz。

模态试验结果与有限元分析结果具有较高的一致性，可以确定试验台符合设计的结构要求。表3为各类模态结果的对比。图7为试验模态振型。

表3 三阶模态频率的模拟和测试结果对比Table 3 Comparison of simulated and tested mode frequencies of three orders of modes

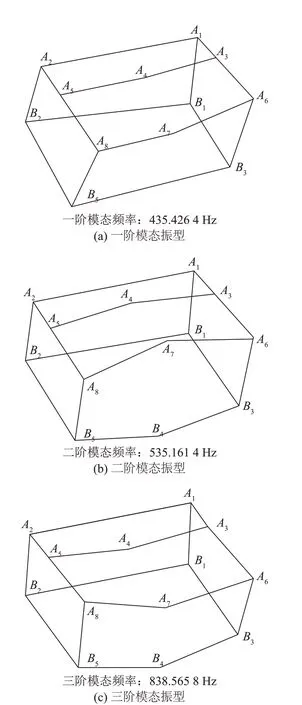
图7 不同模态振型分布示意图Fig.7 Schematic diagram of different mode pattern distributions

3 试验验证

3.1 试验设计

试验分两组工况进行，分别是以试验台为依托的模拟工况和以底盘测功机为依托的运行工况。为了避免多个激励源同时激励产生病态矩阵，更好地与模拟工况对标，在运行工况下，只驱动单个车轮来与模拟工况对标，同时运行工况下轮胎转动，故将参考响应点定于轮芯处。当车辆被底盘测功机拖动时，结构传播噪声与空气传播噪声不可避免地交叉在一起，正常家用车辆的车内声压级较低，频率在400 Hz 以下，车内噪声对振动的影响可以基本忽略，故取驾驶员座椅导轨z向的加速度作为目标响应信号，同时为探究该路噪结构载荷模拟方法能否模拟路面结构激励在车内产生的噪声，在驾驶员右耳处布置了一支麦克风采集噪声信号。

参考响应点及目标响应点传感器布置如图8所示。为尽可能减小空气传播噪声的影响，测试采用整车半消声室的低噪声转鼓来拖动试验车辆，转鼓的声学性能为：在速度100 km·h-1稳态下且没有车辆和其他噪声源时，在转鼓外水平距离1 m、高1 m处测量的噪声水平小于50 dB(A)。

图8 在参考点及目标点的加速度传感器布设Fig.8 Acceleration sensor layout at the target point and reference points

3.2 模拟工况

在驾驶员导轨处及轮芯参考点布置好加速度传感器后，将4个试验台放入各个车轮正下方，然后将3 个微型激振器通过试验台上安装孔固定于车胎，测试使用的微型激振器功率为25 W，在50～500 Hz 频率范围内，激振力的均方根值为1.5 N，实验测试图如图9所示，安装完成后，利用激振器测得模拟工况数据。

图9 路噪结构载荷模拟的测试图Fig.9 Test arrangement for structural load simulation of road noise

在实验过程中，为提高车内响应信号的信噪比，使用功率放大器将20～500 Hz 的扫频信号放大，再输出三路相同的信号以驱动各个微型激振器工作。通过试验台模拟运行工况下左前轮路噪结构载荷，在车内驾驶员耳旁测得的麦克风响应信号的频谱如图10所示。

图10 路噪结构载荷模拟测试中在驾驶员耳旁测得的麦克风响应信号频谱Fig.10 The microphone response signal spectrum measured by the driver's ear in the tests for structural load simulation of road noise

由图10可知，由于微型激振器在50 Hz以下频段频响不足，造成该频段内的车内目标响应信号的幅度较低，但整体上超过背景噪声10 dB，该频段内的信号仍然有效。在50～400 Hz频段，目标响应信号平均超过背景噪声20 dB，信噪比非常高。其他三个车轮的模拟路噪结构载荷激励结果与图10相似，此处不再一一展示。以上结果表明，通过微型激振器模拟的路噪结构载荷作用于系统时，产生的响应信号可以满足传递率计算的需要。

3.3 运行工况

为进一步地将结构路噪分解，避免多个激励源同时激励，更好地与模拟工况对标，故拆除试验车辆的右后轮(试验车辆为前驱车型)，仅让转鼓拖动左后轮，试验系统物理上成为单输入单输出系统。使用转鼓拖动单个非驱动轮具有一定危险性，试验过程中一旦发现车身剧烈抖动应使转鼓紧急刹车，避免发生事故。

验证试验车辆稳定性后，开始试验，将转鼓调成速度模式(V 模式)，将车速稳定在80 km·h-1，开始采集数据，得到运行工况数据。

3.4 试验结果与讨论

利用式(4)～(9)求得两种工况左后轮参考响应点到目标响应点的传递率，验证使用该方法模拟路噪结构载荷的可靠性。测试结果如图11 所示。根据测试结果，发现低于50 Hz频段的模拟工况的相干函数明显偏低，经分析是因为所用的微型激振器为电磁式激振器，设计时存在低频响应较差的缺陷，故导致50 Hz以下频段的相干函数偏低。频率接近400 Hz的区域，模拟工况相对运行工况的相干函数偏低，经分析是因为此处为系统的反共振点，三个微型激振器的安装位置可能偏离车轮正下方，信号输入存在不同步，微型激振器的激励能量远小于转鼓的激励能量导致出现该现象。但总体来看，两种工况相干函数重合度高，且均接近1，证明参考响应信号与目标响应信号具有良好的线性关系。

图11 模拟路噪结构载荷的测试中参考响应信号与目标响应信号的相干函数和传递率Fig.11 The coherence function and transfer rate of the reference response signal and the target response signal in the tests for structural load simulation of road noise

在50～400 Hz频率区间，二者传递率曲线一致性良好，且在该频段在其他工况(不同车速及缓加速)测得的传递率与匀速80 km·h-1的工况结果近似。虽然由于存在橡胶衬套等因素，结构路噪的传递存在一定的非线性，但在稳态或者准稳态工况下，在关注的低频段内车速对传递率的影响可忽略不计。以上试验结果说明所研究方法能较好地模拟路噪结构载荷。

4 结 论

本文通过设计一个试验台来研究一种模拟路噪结构载荷的方法，得到如下结论：

(1) 通过引入外部的激振力对系统进行激励，测试参考点到目标点之间的传递率，对路噪结构载荷进行模拟是有效的。

(2) 该方法可以较为真实有效地模拟50～400Hz频率区间的路噪结构载荷，运用该方法可以避免多个相关激励源同时作用，避免传递率矩阵的求解出现严重偏差。

(3) 该方法可以控制四个车轮下的微型激振器进行不同的输出，以模拟多种不同的工况。

(4) 微型激振器的性能将直接影响试验结果，应尽可能地选用低频性能更好的微型激振器进行试验。

目前本文只研究了路噪结构载荷模拟方法，下一步拟在试验台内部安装一个声源来对路噪声载荷模拟方法展开研究，为相关路噪研究提供更全面的指导。