水下稳态涡流场声传播的数值模拟和实验研究
喻敏,樊丁繁,张烨,刘航
(1.武汉理工大学船海与能源动力工程学院,湖北武汉 430074;2.中国船舶集团有限公司系统工程研究院,北京 100094)
0 引 言
声波探测作为一种直接的、非侵入式的和全局式的测量方法,可用于水下旋涡特性的测量[1-2]。声波在穿过涡流场时,其传播路径发生变化[3-4],由此产生声波相位的变化,相位变化量和涡流场的形态特征密切相关。因此,发展基于涡流场声传播特性发展水下涡流场探测识别技术成为可能,在军事和工程中具有应用前景。
使用声波探测方法进行涡特性的计算首先在超声领域得到了应用。1992年,文献[5-6]提出了在非均匀介质(涡流场)中,引入光学中相位共轭镜的方法对目标的反射声进行聚焦,以达到定位的目的。1997年,Roux等[7]通过实验从接收信号的幅值与相位差两个方面研究声信号穿过涡流场后产生的变化。从1998年开始,文献[8-10]先后使用多种实验装置对水下涡流场进行深入研究,指出涡流同时改变了声波的传播方向和传播速度。2001 年,Pag‐neux等[11]基于射线声学研究了二维空间中的理想涡对高频声波的散射。2005年,Rosny等[12]针对低马赫数涡流场引起的声信号相位跳变量较小、不易测量的问题,采用了TRM 技术来增大相位跳变量、降低干扰,取得了较好的效果。2023 年,陈雨晨等[13]针对介质运动对声传播的影响,建立一种利用高斯波束法求解亚音速运动介质中的声传播模型,认为在海流会明显影响声的传播。
上述文献研究中,多采用理想涡流速分布公式,甚少通过现代计算流体力学(Computational Fluid Dynamics,CFD)方法获取涡流场流速参数。文献[13]虽然采用射线声学方法对运动介质中的声传播进行研究,但没有涉及复杂流场中的声传播问题。本文针对声波通过水下稳态涡流场的数值模拟方法及实验展开研究,首先根据稳态涡流场中的射线微分方程数值模拟声线传播轨迹,然后开展水池超声传感器实验,最后将数值模拟和实验测量的通过涡流场的声信号时延量进行对比验证,证明了本文通过射线声学方法数值模拟水下稳态涡流场声传播的有效性。
1 涡流场声线轨迹数值模拟
涡流场声传播特性的改变,主要表现为通过涡流场的声波振幅与相位的变化[14]。涡流场声传播效应示意图如图1所示,顺流区声速加速,逆流区声速减速,最终导致在接收端声波的相位超前或滞后。
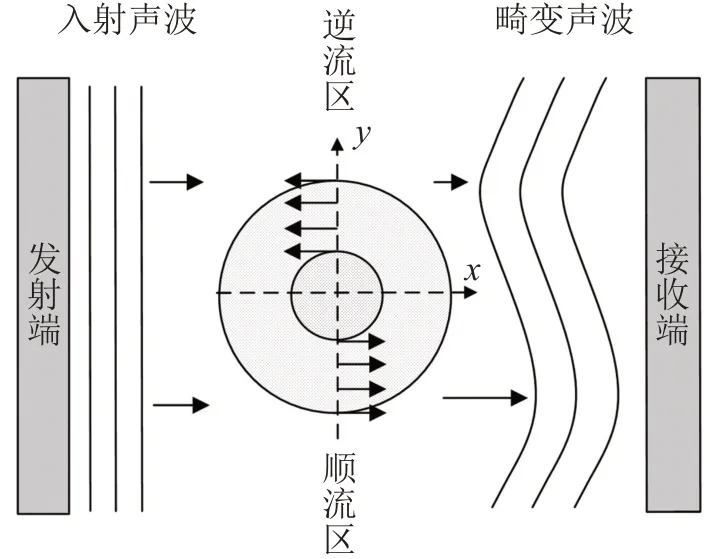
图1 涡流场声传播效应示意图Fig.1 Schematic diagram of sound propagation effect in vortex field
射线声学是几何声学的近似理论,适用于解决高频情况下的声传播问题。基于射线理论可以有效模拟声波通过涡流场的声线轨迹及信号变化,具有直观、计算效率高的特点。为模拟声波通过涡流场的声线轨迹,根据稳定移动介质中的程函方程[15],推导出可进行声线轨迹模拟计算的稳态涡流场射线声学微分方程组:
式中:γ(r)为涡度;α表示声线掠射角;u表示涡流场速度。
声线轨迹数值仿真示意图如图2所示。在理论计算过程中,对于某一条声线s,固定每步迭代中x方向的增量Δx,通过式(1)获取y方向的增量Δy,进而确定该声线的轨迹。

图2 声线轨迹数值仿真示意图Fig.2 Schematic diagram of sound ray numerical simulation
声线通过涡流场后的数值模拟轨迹如图3 所示。由图3可知,通过涡流场的声线掠射角发生偏移,越靠近涡核中心其掠射角变化越大,并在涡核后方形成声线焦散区。仿真中,涡流场切向速度(简称:流速)r分布采用二维稳态兰金涡流(Rankine vortex):

图3 a=10 mm,Ma=4.6×10-2时的声线传播轨迹Fig.3 Sound ray propagation trajectory when a=10 mm,Ma=4.6×10-2
式中:r表示涡流场某一测点到涡核中心点的距离,a为涡流场流速最大处涡核特征半径;Γ=2πacMa,定义为涡流环量;c=1 500 m·s-1为水中声传播速度;Ma为马赫数,定义为涡流最大切向速度与声速之比。
本文数值模拟结果与文献[16]实验结果进行对比,在相同条件设置下,声信号相位差计算结果如图4所示。由图4可见,相位差的数值模拟结果与文献实验结果整体上吻合较好。为了进一步验证数值模拟方法,本文设计并搭建了超声测量涡流场实验平台,开展相关实验验证。
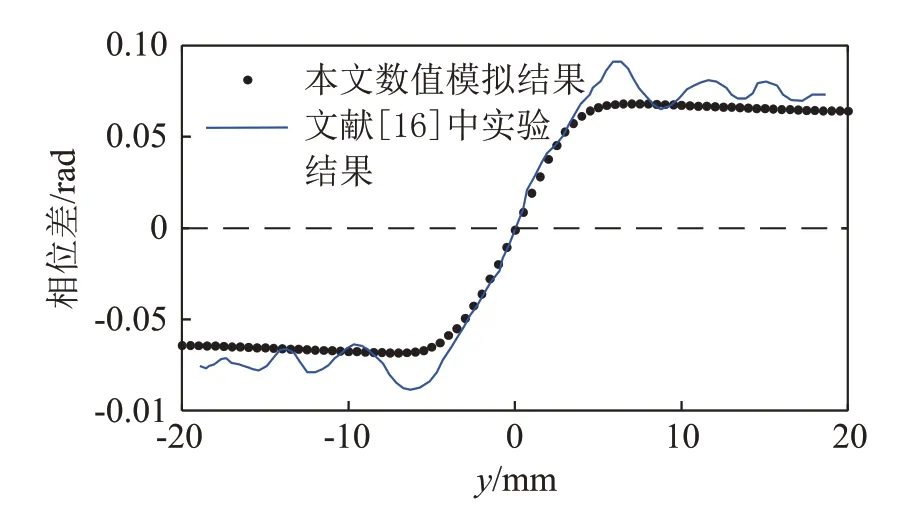
图4 声信号相位差本文数值模拟结果与文献[16]实验结果的对比Fig.4 Comparison between the numerical simulation result in this paper and the experimental result from reference[16] regarding the phase difference of acoustic signal
2 实验装置及涡流场参数
2.1 实验仪器设备
实验设备实物图如图5(a)所示。实验通过螺旋桨产生稳态涡流场,螺旋桨直径d=60 mm,固定在尺寸为2 m×0.6 m×0.8 m 的亚克力长方体水池中,实验布置如图5(b)所示。

图5 实验设备实物图及实验布置示意图Fig.5 Photo of the experimental equipment and schematic diagram of experiment layout
螺旋桨位于整涡管顶部,由电机带动旋转产生涡流。涡流流出整涡管后,使用超声传感器发射和接收通过涡流的声信号。为保证两个超声传感器中轴在同一条直线上,超声传感器刚性固定在同一移动滑台上。水池装有导轨和滑尺,便于精确标定传感器位置。针对螺旋桨高速旋转产生的振动,在实验中将造涡装置和测量装置分别固定在两组滑台上,在螺旋桨与其固定滑台联接处使用螺丝螺母固定并加垫片以减少振动。仪器设备型号及参数如表1所示。

表1 实验仪器设备型号及参数Table 1 Model and parameters of experimental equipment
2.2 涡流场CFD仿真
由于实验中的涡流场速度分布不易获取,本文基于现代流体仿真软件Fluent,根据实验布置对涡流场分布进行数值仿真。本文使用Design Modeler建模软件建立三维模型。计算域的划分与边界条件的设置如图6所示。采用ICEM前处理软件划分网格,使用六面体结构化网格对整体区域进行划分,并在旋转域表面进行局部加密,以更好地模拟近壁流动。
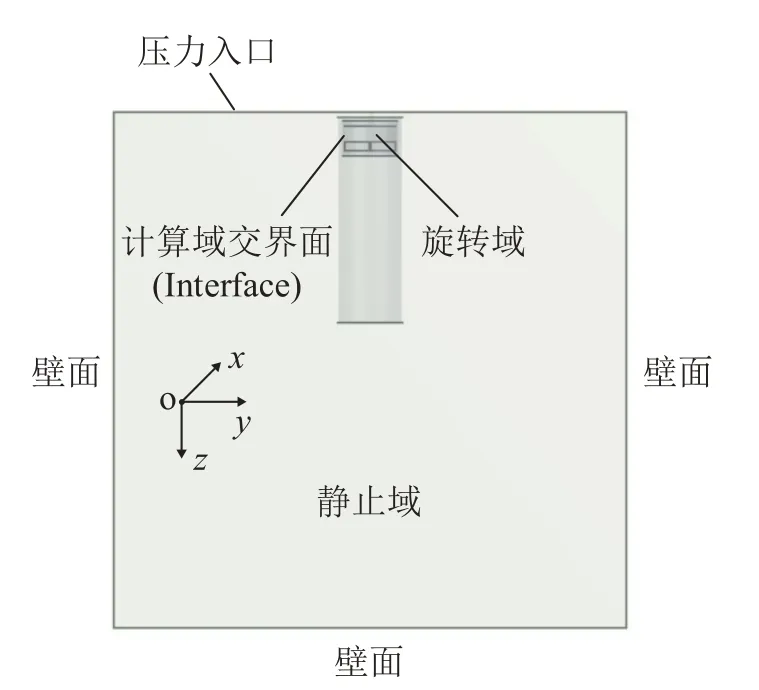
图6 数值模拟计算域Fig.6 Numerical simulation computing domain
螺旋桨所在的旋转域采用稳态(Moving Refer‐ence Frame,MRF)方法,并绕z轴以1 400 r·min-1的转速旋转。基于有限体积法求解RANS方程,湍流模型选用标准k-ε模型,调用标准壁面函数进行计算。采用三维双精度基于压力隐式求解器,耦合方式采用SIMPLE 算法,离散格式采用二阶迎风格式。
2.3 涡流场参数
定义整涡管出口所在平面为z=0平面,分别在整涡管出口下端z=10、30和50 mm处取截面,得到涡流场速度分布矢量图如图7所示,其中z=10 mm截面上的流速分布云图如图8所示。由图7、8可以看到涡流场在流出整涡管后向外消散,符合自由场涡流运动规律。
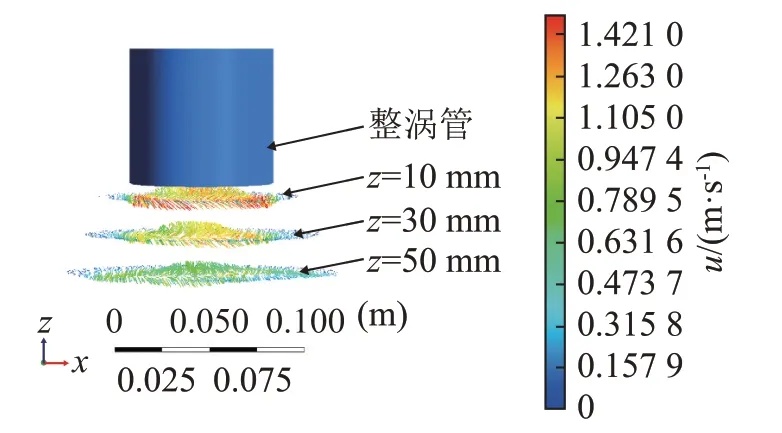
图7 涡流场速度分布矢量图Fig.7 Velocity distribution vector diagram of vortex field
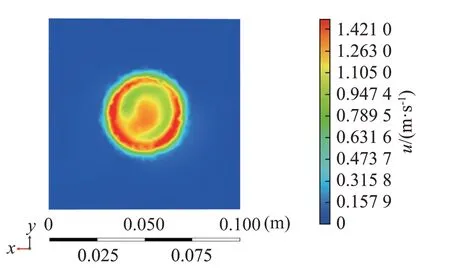
图8 在z=10 mm处的平面涡流场速度云图Fig.8 Velocity cloud diagram of the plane vortex field at z=10 mm
涡流流速最大位置对应涡核半径尺寸,由图8可知,z=10 mm平面上的最大速度umax=1.258 m·s-1,判断涡核半径a=30.6 mm。根据z=10、30和50 mm处的流场速度数据可得到不同截面的涡流场主要参数,如表2所示,为基于射线声学的涡流场声传播数值模拟方法提供输入参数。

表2 最大切向速度和涡核半径Table 2 The maximum tangential velocity and vortex core radius obtained by simulation
3 实验研究
3.1 实验工况设置
为避免发生声衍射,声波波长需远小于涡流场尺度。根据表2中的参数,选择声波的发射频率为2 MHz,幅度为3 V,示波器采样率为1.0 GHz。实验工况通过改变两个传感器位置获取不同截面的声信号时延。在整涡管出口位置下端10、30和50 mm处分别设置3个测量平面,如图9(a)所示;在每个平面上,依次间隔10 mm设置a~k共11组测点,测点布置示意图如图9(b)所示。
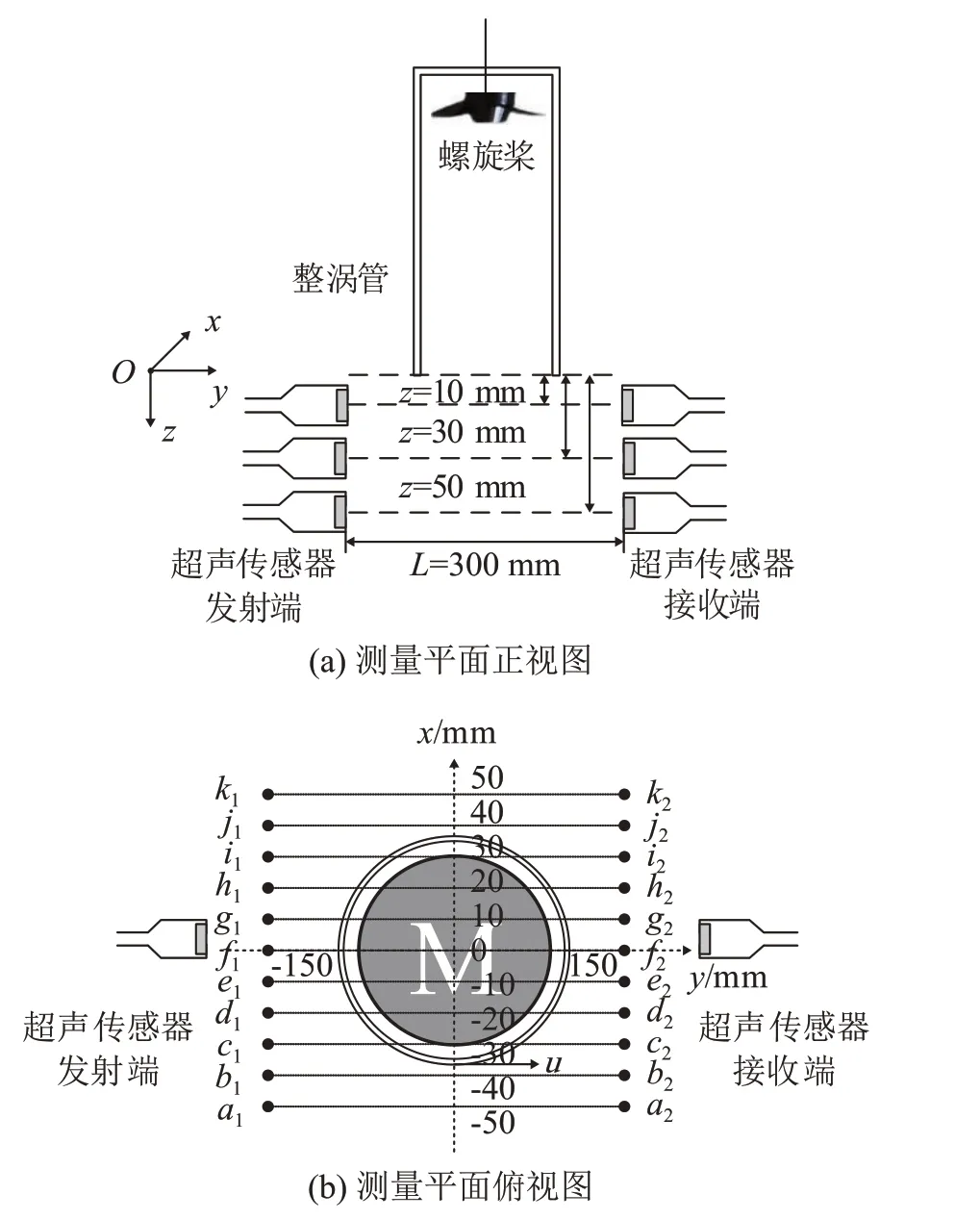
图9 测量平面正视及俯视示意图Fig.9 Schematic diagram of the front and top views of the measuring plane
按照表3所示工况在每个测量平面上依次对11个测点进行测量、记录、存储数据。每处测点测量5次。其中,工况1是无涡情况,只需测一组工况,即以z=10 mm 平面上的测点a测量无涡工况下声时延。
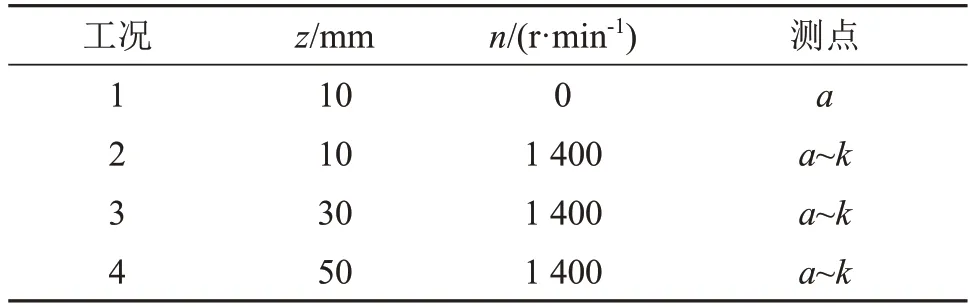
表3 实验工况表Table 3 Table of experimental conditions
3.2 数据处理与分析
针对有涡情况,分别获取有涡与无涡工况下的超声传感器接收端的时域信号。其中一组接收信号的对比如图10 所示。采用互相关算法即可得到此组数据的时延量为2.74×10-8s。
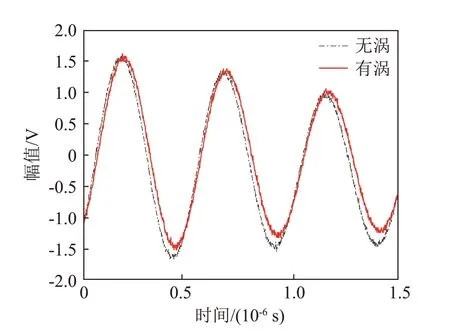
图10 有涡和无涡工况下接收信号对比Fig.10 Comparison of the receiving signals in the vortex and no vortex conditions
不同截面的时延计算结果如图11 所示。图11中实线部分为根据实测数据拟合得到的时延曲线,虚线部分为针对表2中不同截面处的涡流场,采用基于射线声学的数值模拟方法计算得到的声信号时延值。由图11可知,时延曲线呈现“S”形变化趋势,说明涡流场对声传播有明显影响。随着z值增大,时延最大变化量减少,即涡流场最大切向速度变小;时延最大变化量对应的x值增大,即涡流半径增大,说明涡流在向下运动的过程中不断扩散。
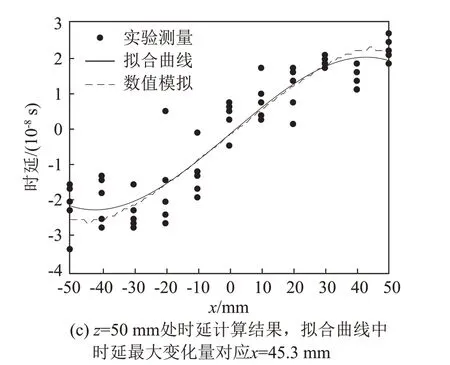
图11 实验测量时延数据及拟合曲线Fig.11 Time delay data and their fitting curves obtained by experimental measurement
采用相位重构算法[9],根据实测的时延拟合曲线反演出涡流场流速分布,并与CFD 仿真流速数据以及理想Rankine涡流速数据进行对比分析,结果如图12所示。由图12可知,CFD仿真得到的流场速度分布与实测数据反演流场速度分布更为接近,而根据式(2)计算的Rankine涡流速分布在最大流速两侧速度衰减较慢,这是因为实验环境与理想流场假设存在差异的。而基于CFD 计算涡流场数据,条件设置与实验条件一致,相较于式(2)更能反映出真实的流场分布。
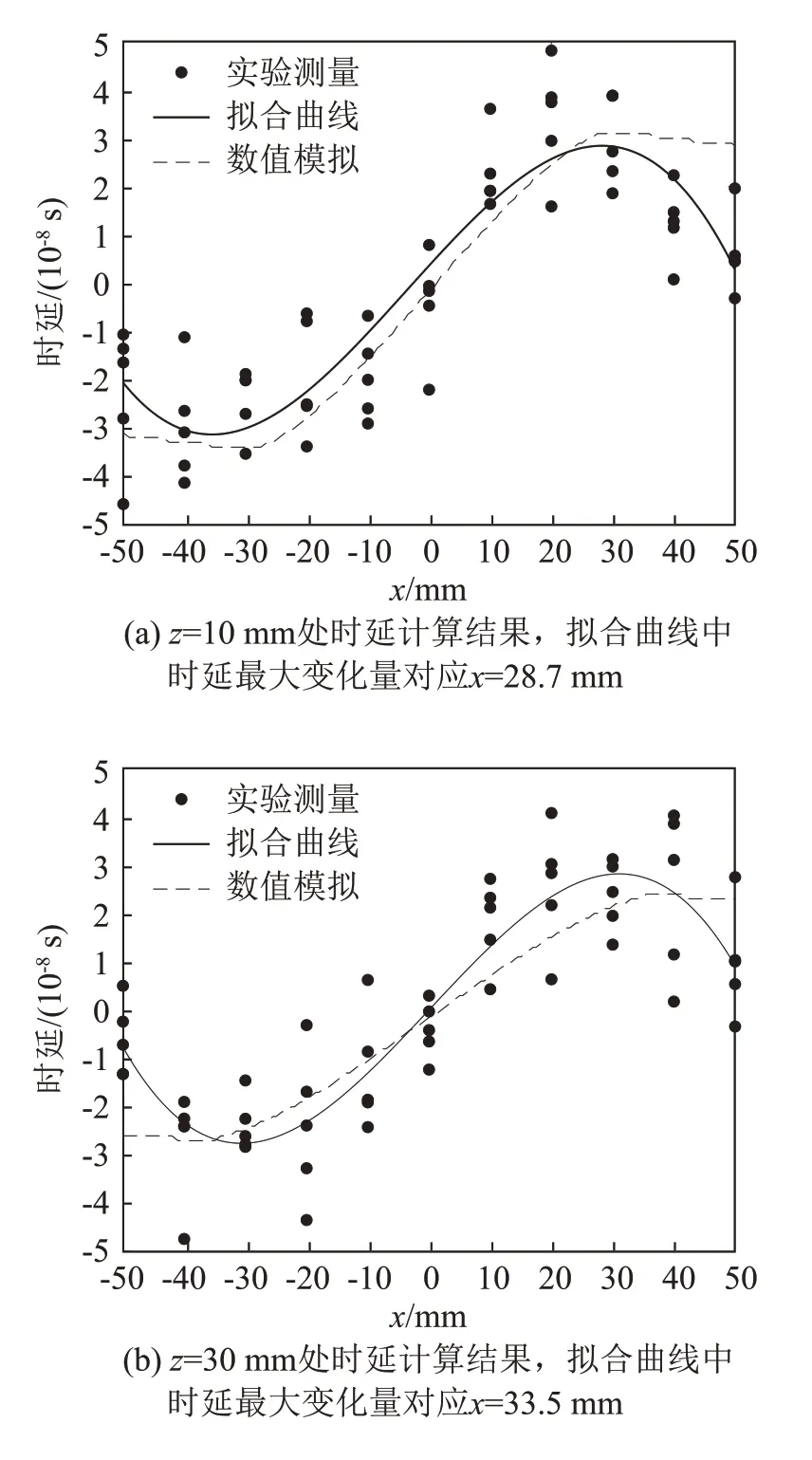
图12 在z=10 mm处的三组平面流速分布数据对比图Fig.12 Comparison of three sets of flow velocity distribution data in the plane at z=10 mm
以数值模拟的时延为真值,采用均方根误差公式,计算图11 中实测时延拟合曲线和数值模拟曲线之间的误差。由于数值模拟中所代入的流场分布是理想Rankine涡流速,在最大流速两侧与实际流场分布有一定差距,因此只计算最大流速中间对应的时延曲线误差,计算结果如表4 所示。由表4可知,数值模拟计算的时延与实验测量值基本吻合,误差均小于10%,说明本文提出数值模拟方法的有效性。
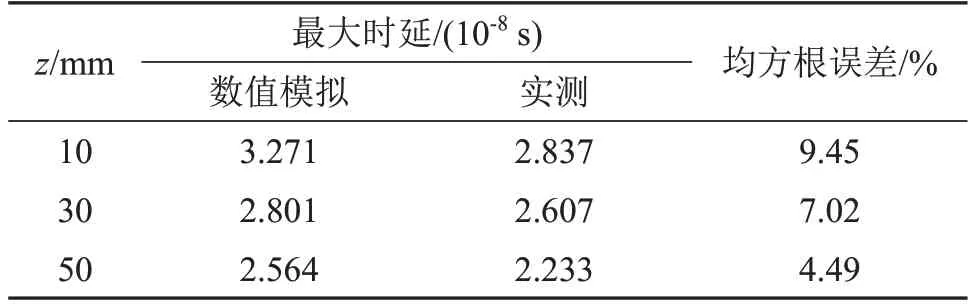
表4 时延数据与误差分析Table 4 Time delay data and error analysis
4 误差分析
本实验主要针对声时延量进行测量,该时延量为小量,为了进一步分析实验结果的可信性,下面针对影响时延测量的误差因素进行讨论。
4.1 传感器指向性
实验中所使用的超声传感器具有指向性,主瓣-3 dB处的开角Φ为4°±1°,可通过改变发射端与接收端轴向偏移量研究指向性对时延测量的影响。
在整涡管出口下方z=10 mm 平面按照图13 所示进行传感器的布置,测点a处发射端与接收端中轴严格对齐,随后依次偏移5 mm 的测点设为b~e测点,在各测点处测量有涡和无涡条件下的声信号。由于超声传感器指向性的影响,不同测点处的声信号幅值发生改变。改变接收信噪比(Signal to Noise Ratio,SNR),每个测点的信噪比测量结果如表5所示。

表5 不同测点的信噪比测量结果Table 5 Measurement results of SNR at different positions

图13 传感器布放位置示意图Fig.13 Schematic diagram of the sensor placement
信噪比的改变将直接影响时延估计的精度。根据本文实验条件,计算互相关时延估计算法在不同信噪比条件下的时延误差如图14所示。由图14可知,当信噪比大于10 dB时,时延估计误差均小于5%。由表5可知,实验时发射端与接收端中轴偏移量小于10 mm就可以保证10 dB以上的信噪比。本实验中两个超声传感器被刚性固定在同一移动滑台上,中轴偏移量远小于10 mm,信噪比较高,因此超声传感器指向性对实验结果影响较小。
4.2 整涡管
在z=10 mm平面上,整涡管的存在可能会对声波产生反射、透射和衍射等产生影响。整涡管出口干扰示意图如图15 所示。由于本实验所使用的传感器发射和接收均具有较窄的指向性,则整涡管的存在对声信号所产生的影响较小,下面通过实测数据分析整涡管对本实验声传播的影响。
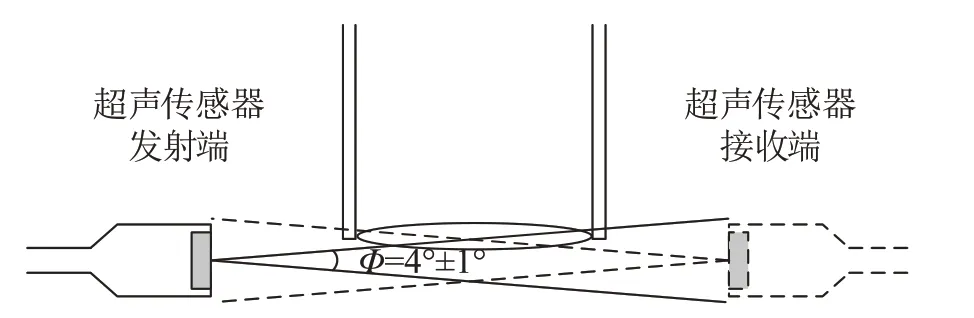
图15 整涡管出口干扰示意图Fig.15 Schematic diagram of vortex tube outlet interference
在无涡条件下,在z=10 mm平面处,对存在整涡管和无整涡管两种情况,分别测量声波从发射端到接收端的传播时间。两种情况下传播时间相对误差为2.27%,即整涡管对z=10 mm平面上的声时延测量影响较小,其他平面离整涡管距离更远,则影响将更小。
5 结 论
本文围绕水下稳态涡流场的声传播展开研究,给出了稳态涡流场中的声线传播的微分方程,通过基于射线声学的数值模拟方法计算声波通过涡流场的时延,并与实验测量结果进行对比分析,得到如下结论:
(1) 基于射线声学的数值模拟方法能有效计算声波通过涡流场后的时延,数值模拟误差小于10%。
(2) 通过现代CFD方法获取水下稳态涡流场的流速分布,较理想涡流场流速的理论公式更接近实际涡流场声速的分布。
(3) 通过误差分析可知,本实验中由传感器指向性和整涡管产生的误差较小,验证了本实验测量结果的可靠性。

