基于声学黑洞的复合隔声结构声学特性研究及试验

余勇花，吴天歌，杨淇，叶锦啸，夏兆旺,2

(1.江苏科技大学能源与动力学院，江苏镇江 212003；2.江苏海事职业技术学院船舶与海洋工程学院，江苏南京 211170)

0 引 言

随着社会的发展，噪声污染越来越受到人们的重视[1-3]。复合隔声结构一般由平板、阻尼层、穿孔板及多孔吸声材料等组成。相较于传统单板结构，在面密度相近时，复合隔声结构具有更好的隔声性能[4]。夏兆旺等[5]研究了嵌入式质量块对隔声门低频段隔声性能的影响，通过有限元法建立两个相邻混响室计算隔声门的隔声量(Sound Transmis‐sion Loss,STL)。Liu[6]研究了板、空气、多孔材料间的耦合关系，分析总结了结构组合类型对复合板隔声性能的影响。

声学黑洞的引入为复合隔声结构的发展增添了新的活力[7]。声学黑洞的结构厚度满足幂指数函数形式。在理想情况下弯曲波速可以减小到0，可实现弯曲波的零反射[8]。1989 年，Krylov[9]研究了楔形的一维梁结构操纵弯曲波的传播。王博涵等[10]研究了内嵌声学黑洞薄板振动数值模拟方法，结果表明合理调节声学黑洞区域的厚度梯度变化尺度以及幂律会改变局部模态参数。刘波涛等[11]研究了声学黑洞轻质超结构的低频带宽高效隔声机理，设计了一种针对低频的新型声学黑洞超结构。王小东等[12]针对直升机驾驶舱的噪声问题，提出了基于声学黑洞的两种减振降噪方案，在结构总质量不增加的情况下，室内平均噪声水平在1/3倍频程内降低了3～10 dB。

本文将声学黑洞引入复合隔声结构的设计中，推导了包含多孔材料与穿孔板等参数的复合隔声结构传递矩阵，进而得到复合隔声结构隔声量，通过有限元法建立的声学黑洞复合隔声结构仿真模型，分析了声学黑洞的数量、黏弹性阻尼层、半径等参数对结构隔声量的影响规律。本文的研究结果为高隔声量、低面密度的复合隔声板结构设计提供了新思路。

1 声学黑洞复合隔声结构理论基础

1.1 声学黑洞结构振动波传递特性

嵌入二维声学黑洞的圆板如图1所示。原板厚度和半径之间的关系式为

图1 嵌入二维声学黑洞的薄板Fig.1 Plate embedded with a two-dimensional ABH

式中：h为黑洞板的厚度；r为黑洞的半径；ε为常数；m为正有理数，被称为黑洞效应指数因子；b为黑洞中心到坐标原点的距离；hp为均匀板区域的厚度。弯曲波在各向同性薄板中的传播速度为，

式中：B为弯曲刚度，B=Eh3(x) [12(1-v2)]；E为杨氏模量，v是泊松比；ω是角频率；M是板的面密度。

1.2 复合隔声结构隔声特性

对复合隔声结构进行简化处理：将复合隔声结构看作n层不同材质的组合结构，每层结构为独立的声学单元，声波从一侧入射后，从另一侧辐射，则通过复合隔声结构两侧的声压与速度可建立四端参数模型，模型示意图如图2所示。

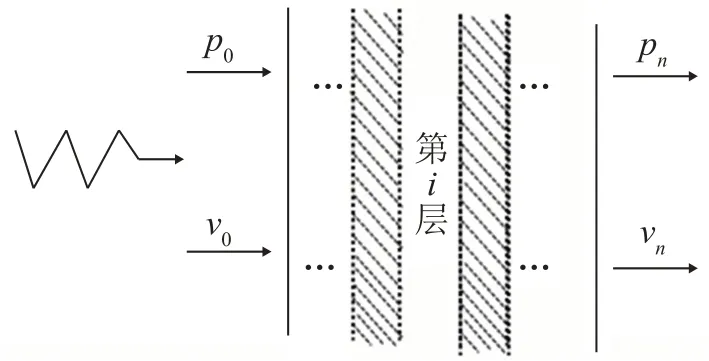
图2 复合隔声结构四端参数模型示意图Fig.2 The four-pole parameter model of multilayer sound insulation structure

以第i层为对象，其前后表面的声压和速度可通过二阶传递矩阵表示：

式中：li为材料层厚度，ci为材料层的速度，ki为材料层的波数，ω为角频率，ρi为第i层介质密度，Ki为第i层介质的体积弹性模量。

第i层前后表面的声压和速度可通过二阶传递矩阵表示：

式中：pi与vi分别为入射声压与速度；pi+1与vi+1分别为辐射声压与速度。

第i层介质的声压pi与速度vi间的关系用其阻抗表示：

由式(5)可得到：

由式(3)和式(4)可得到第i层声压传递关系：

式中：k0为空气的波数，ρ0为空气的密度。

则复合隔声结构声压总的传递关系为

进而得到复合隔声结构的隔声量为

2 复合隔声结构的声学仿真模型

2.1 隔声仿真声腔建模

在隔声结构隔声性能的仿真分析中，需要构建模拟试验测试的双混响空间。设计一个满足均匀声场的混响空间，混响空间的长宽高比例为Lx∶Ly∶Lz=0.9∶1.2∶1.4。在混响室内壁设置不同半径的半球形突起以实现混响空间内的每个频段都具有很好的扩散效果[13]。在商业软件COMSOL 中建立两个混响室，其中声源室尺寸为1 m×1.34 m×1.56 m，受声室的尺寸为1.5 m×2 m×2.3 m。在混响室按照ISO 10140—2[14]的附录D建立点声源和测点，声源为无指向性声源。模型整体采用六面体网格，且满足每个波长内至少包含6个单元。隔声分析仿真声腔模型如图3所示。

图3 隔声分析的声腔模型Fig.3 Acoustic cavity model for sound insulation analysis

2.2 复合隔声结构仿真模型验证

隔声试验采用混响室-混响室隔声试验方法，测试所用的混响室尺寸为：声源室5.9 m×5.6 m×4.9 m，接收室5.9 m×3.7 m×4.1 m，依据ISO 10140—2[14]中的测试标准，参照ISO 717—1[15]中的评价标准进行单值评价。

隔声量的计算公式为

式中：ζ表示声源位于位置1或位置2；Lζ1、Lζ2分别为经背景噪声修正后的声源室和接收室能量平均声压级；S为试件安装测试洞口面积；D=0.16V/TR为接收室吸声量，V为接收室容积，TR为接收室混响时间。复合隔声结构的试验平均隔声量为

实验构件安装在声源室与受声室间的窗口。试验布设照片如图4所示。

复合隔声结构模型由隔声板、阻尼层、多孔材料层、中间薄板以及穿孔板组成。复合隔声结构如图5所示。

图5 复合隔声结构示意图Fig.5 Schematic diagram of the composite sound insulation structure

复合隔声结构的平面尺寸为1 m×1 m，多孔材料为玻璃棉，外平板与中间薄板为钢板，穿孔板为铝板，阻尼材料为黏弹性阻尼胶，各层材料参数如表1和表2所示。

表1 复合隔声结构的材料参数Table 1 Material parameters of composite sound insulation structure

表2 多孔材料参数Table 2 Porous material parameters

整个复合隔声结构安装于双混响室之间，穿孔板侧位于声源室，隔声板侧位于接收室，隔声板四周采用固定约束。其中外平板厚度为1.5 mm，多孔材料均为25 mm，中间薄板0.1 mm，阻尼层厚度为2 mm，穿孔板厚度为1 mm(穿孔率为10%，孔径为4 mm)，试验与仿真隔声量对比如图6所示。

图6 隔声量的测试与仿真结果对比Fig.6 Comparison of simulated and tested results of STL

由图6可知：在160～5 000 Hz频段范围内，复合结构隔声量的仿真值为36.6 dB，实验单值为36.1 dB。复合结构隔声量的试验值与仿真值误差为0.5 dB。试验与仿真对比结果表明：复合隔声结构隔声量仿真与试验结果具有较好的一致性，因此采用的仿真分析方法是可行的。

图7 为1.5 mm 钢板与1.5 mm ABH 板的隔声量对比图。由图7可知：在160～1 000 Hz频率范围内，1.5 mm钢板的仿真结果与试验结果具有很好的一致性，采用的仿真方法是可行的。在整个频段内，相较于1.5 mm普通钢板，ABH板的隔声性能更好。

图7 1.5 mm钢板与1.5 mm ABH板隔声量对比图Fig.7 Comparison of STLs between 1.5 mm steel plate and 1.5 mm AHB steel plate

3 声学黑洞复合隔声结构隔声性能影响因素分析

3.1 声学黑洞复合隔声结构隔声量分析

在保持复合隔声结构主要尺寸不变的基础上，在隔声板中心位置添加一个黑洞结构。黑洞结构的半径为50 mm，幂指数m=2，截断厚度为0.5 mm，则黑洞中心剖面的厚度表达式为h(x)=0.4x2+0.5。黑洞复合隔声结构如图8所示。

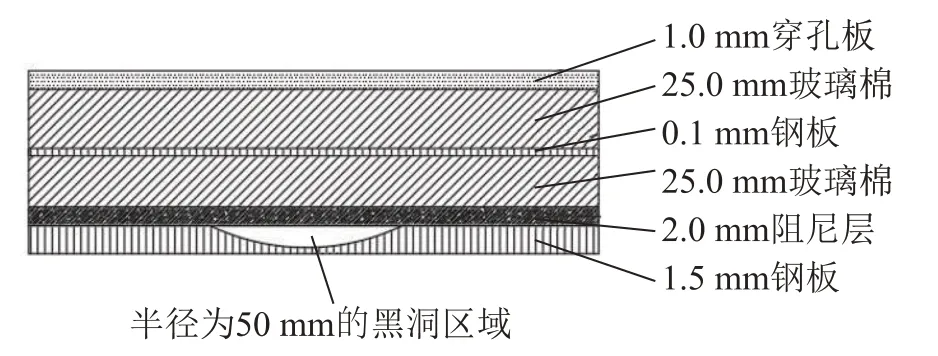
图8 黑洞复合隔声结构Fig.8 Composite sound insulation structure with ABH

复合隔声结构采用六面体单元划分，且满足每个单位波长至少包含6个单元的原则。将黑洞薄板结构沿板厚方向划分为3层网格，其中厚度均匀区域最大单元的边长为8.71 mm，黑洞区域最大单元的边长为4.91 mm。复合隔声结构的隔声量计算结果如图9所示。

图9 复合隔声结构与声学黑洞复合结构隔声量对比Fig.9 Comparison of STLs between the normal and the ABH based composite sound insulation structure

由图9可知：在160～1 000 Hz频率范围内，声学黑洞复合隔声结构的隔声性能明显优于普通复合隔声结构。其中在160～315 Hz 频率范围内，声学黑洞每个频点处的隔声量比普通复合结构高2.9 dB以上。在整个分析频段内，声学黑洞复合隔声结构相比复合隔声结构，隔声量平均提高了1.9 dB。因此，声学黑洞能改善复合隔声结构中低频段的隔声性能。

3.2 阻尼对隔声性能的影响

在ABH 区域粘贴阻尼可显著改善截断厚度对弯曲波聚集的不利影响，阻尼材料参数如表3 所示。粘贴阻尼结构的钢板示意图如图10 所示。在不改变材料参数的条件下，研究了敷设黏弹性阻尼材料对黑洞复合隔声结构的隔声性能影响，结果如图11所示。

表3 阻尼层材料参数Table 3 Material parameters of damping layer

图10 带阻尼层的AHB板Fig.10 ABH plate with a damping layer

图11 敷设阻尼层对黑洞板隔声量的影响Fig.11 Effect of pasting a damping layer on STL of the ABH plate

由图11 可知：在160～1 000 Hz 频段范围内，阻尼层对复合ABH 板结构的隔声量影响主要集中在中高频区域。在400～1 000 Hz频率范围内，敷设阻尼层后平均隔声量增加了3.1 dB。

3.3 黑洞数量对隔声性能的影响

在其他参数不变的条件下，研究声学黑洞的价目数对声学黑洞复合隔声结构隔声量的影响。黑洞的个数及排列方式如图12 所示，仿真结果如图13所示。

图12 不同个数的黑洞及排列方式Fig.12 Different numbers of black holes and their arrangements

图13 黑洞个数对复合隔声结构隔声量的影响Fig.13 Effect of the number of ABH on STL of the structure

由图13 可知：在160～1 000 Hz 频率范围内，增加ABH 数量并不能提高结构的隔声量，反而会降低其隔声量。在此频率范围内，结构传递损失受劲度控制，增加ABH 的个数会降低结构的刚度。在不同频段内，每个声学黑洞的能量聚集效应表现出明显的差异，嵌有单个AHB的复合结构在160～1 000 Hz频率范围内均具有较好的隔声效果。

3.4 黑洞半径对隔声性能的影响

在声学黑洞个数为1、其他参数不变时，研究声学黑洞半径对复合结构隔声性能的影响。黑洞半径分别为0.05、0.08、0.12、0.15、0.18 m，仿真结果如图14所示。由图14可知：在160～315 Hz频段内，当半径为0.05 m和0.08 m时，其隔声效果较为接近，当黑洞半径继续增大后，隔声效果略有下降，但随着半径增加趋于稳定。在500～1 000 Hz频段内，声学黑洞半径每增加0.03 m，平均隔声量增加0.8 dB以上。

图14 黑洞半径对复合隔声结构隔声量的影响Fig.14 Effect of ABH radius on STL of the structure

4 结 论

本文研究了声学黑洞复合隔声结构的声学特性。建立了复合隔声结构的声学仿真模型，并进行了试验验证。进一步研究声学黑洞复合隔声板与普通复合隔声板的隔声量，通过对比发现，声学黑洞复合隔声板对提升隔声量有显著效果。最后，通过研究声学黑洞复合隔声结构的阻尼层、声学黑洞数量以及声学黑洞半径对隔声量的影响，得到以下结论：

(1) 在160～1 000 Hz 频段内，声学黑洞复合隔声结构的隔声量比普通复合隔声结构的隔声量平均增加了1.9 dB。

(2) 在声学黑洞复合隔声结构的黑洞结构中敷设黏弹性阻尼材料，在400～1 000 Hz 频率范围内，隔声量平均增加了3.1 dB。

(3) 声学黑洞数量的增加并不能提升复合隔声结构的隔声量。在实际应用中，嵌入单个ABH 即可达到较好的隔声效果。

(4) 在500～1 000 Hz 频段内，声学黑洞半径每增加0.03 m，平均隔声量增加0.8 dB。