基于光声差分衰减频谱的骨质评估仿真研究
余东,解维娅,封婷,程茜
(1.同济大学物理科学与工程学院声学研究所,上海 200092;2.南京理工大学电子工程与光电技术学院,江苏南京 210094)
0 引 言
生物医学光声是近年来发展起来的一种非侵入式和非电离式的新型生物组织检测方法[1-2]。当不同波长的脉冲激光照射到生物组织时,组织中不同生物分子对光的吸收将产生超声信号,这种由光激发产生的超声信号被称为光声信号[3]。光声技术在评估骨质疏松症方面具有显著优势,它既能提供骨矿物质、骨髓、血红蛋白、胶原蛋白等分子信息又能评估骨骼微结构信息和力学状态,在疾病的诊断中显示了巨大的潜力。
光声技术在骨质评估中的研究已有一些成果。密歇根大学的Wang课题组研究了使用热光声测量和光声光谱分析两种技术评估大鼠小梁骨的骨矿物质密度和骨微结构的可行性,并且利用光声方法研究了不同波长处骨头的光声吸收谱和各种化学成分的光声谱[4-6]。Lashkari课题组通过双背向散射超声和光声雷达系统评估皮质骨和小梁骨的结构和密度变化[7-8]。Steinberg课题组使用了双模态多光谱光声系统来量化骨髓中的血脂比,该血脂比与长骨中的分子变化有关[9]。本课题组前期研究了使用光声时频谱分析方法评估骨矿物质密度、骨微结构和化学成分的可行性[10-11],利用多波长光声分析技术在数值模拟和离体实验中评估了动物模型和人体骨骼标本中的胶原含量[12],还提出了一种用于定位和分割人体跟骨光声信号空间信息的超声引导的光声骨质评估方法,从而可以从其他信号中分离出小梁骨的信号[13]。
在上述文献报道中,通常采用激光扩束后覆盖整个骨样本以激发光声信号的方式。骨小梁、骨髓或者微血管等分布式的光吸收分子激发出的光声信号在固液两相多孔结构上形成复杂的多传播路径,最终检测到的信号是分布式骨微结构与分布式光声信号相互作用的结果,即在时间域与空间域上多维信息混叠的结果,这给定量分析骨微结构增加了难度和复杂度。
为了更准确地量化评估骨微结构信息,本文对PAT系统进行改进:将扩束式光源改为弱聚焦式光源以分离局部光声信号,在辐照光斑中心与试样中心连线上设置一对远、近检测点以获取差分衰减频谱(Differential Attenuation Spectrum,DAS),并通过轴对称环形扫描方式考察骨微结构各向异性对声速和DAS 的影响。本文通过数值仿真计算和验证了松质骨的孔隙率与PADAS 的相关性;提取了相应的衰减频谱特征参数,探讨了其进行骨质评估和诊断的潜力。
1 光声信号的数值模拟仿真与分析
1.1 松质骨样本模型
为了研究松质骨的孔隙率φ对光声信号衰减频谱的影响,从人跟骨CT 图中提取的直径为13.11 mm的圆形松质骨样本作为本文的仿真对象,如图1中1号骨组织所示,白色代表骨小梁,主要由骨矿物质构成,骨小梁间隙的黑色部分代表骨髓,圆形骨样本外侧黑色部分为耦合介质(水)。为模拟骨质疏松时孔隙率的变化,对上述图像进行二值化处理,提高二值化函数阈值,大于阈值的部分赋值1,即为白色,反之赋值0,为黑色,从而获得骨小梁逐渐变细,孔隙率逐渐变大的样本图像,如图1中2号~5号所示。

图1 不同孔隙率的松质骨图片Fig.1 Pictures of cancellous bone with different porosities
图1中5块松质骨样本的孔隙率如表1所示。

表1 不同松质骨样本的孔隙率Table 1 Porosities of different cancellous bone samples
1.2 光声激励-检测系统的改进
本文将传统的PAT 系统改进为偏心激励-差分检测模式,如图2所示。图2中,黑色代表骨小梁,白色代表骨髓,红色圆形区域为光声源,灰色长方形为检测点A 和B 所在位置。如图1 所示,采用光斑直径为2 mm 的弱聚焦脉冲光源辐照在图1中的骨头样本上激发局部的光声信号,光斑与圆形样本外缘内切,辐照区域为感兴趣区域(Region of Interest,ROI)。以光斑中心与骨样本中心连线为检测基准线,在样本外侧沿基准线设置一对近端和远端光声信号探测点A和B以获取差分光声信号,A和B 距骨样本中心距离均为8 mm;骨样本可围绕其中心旋转,即对骨样本进行环形扫描检测不同方向的ROI,以研究骨微结构的各向异性对声速和衰减频谱的影响。激光波长为骨矿物质的特征吸收波长,并假设仅由骨矿物质吸收,骨髓等其他物质不吸收该波长激光的能量。

图2 偏心激励-差分检测模式的光声系统示意图Fig.2 Photoacoustic system diagram of the eccentric excitation-differential detection mode
1.3 松质骨样本的光声数值仿真参数
为研究松质骨孔隙率对光声信号的影响,本文利用Matlab软件(R2018a)的k-wave工具包模拟松质骨样本在光源激励下产生和传播的光声信号[14]。仿真参数设置如下:骨小梁中的声速为3 200 m·s-1,骨髓中的声速为1 500 m·s-1,骨小梁的密度为1 850 kg·m-3,骨髓的密度为1 000 kg·m-3[14],骨松质的声衰减系数为9.94 dB·(MHz·cm)-1[15],骨松质四周耦合介质的参数均采用水的各项声学参数;采样频率为500 MHz,数值模拟仿真时长为15 μs,确保远端B检测点也可以采集到ROI产生的光声信号的完整直达波。
同时,为了研究骨松质的光声衰减频谱是否存在各向异性,在仿真模型中,保持激光和检测点的位置不变,使每块圆形骨组织样本绕自身中心旋转,以30°为间隔获取骨组织样本的12组光声信号。
1.4 快波声速的估算及有效信号范围的确定
图3 给出了1 号骨组织样本在某一个角度下,A、B检测点接收到的时域信号。
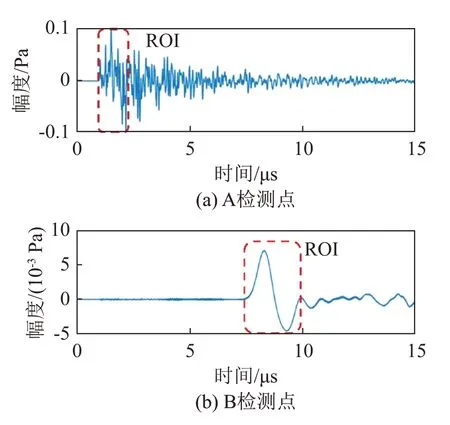
图3 在A、B检测点的有效信号时长示意图Fig.3 Schematic diagram of the effective signal durations detected at the points A and B
由于光声源在空间上有一定分布,光斑不同位置处的信号到达A检测点有时间差,为了确定A检测点有效信号的时间范围,首先根据B检测点接收到的直达波初始时刻及其到光声源的距离,计算出5 块骨组织样本的不同方向上各12 组信号的声速,每块骨组织样本的最大、最小和平均声速如表2所示。由表2 可知,在不同方向上的声速差别较小,波动均小于1%。根据每块样本的声速和光斑直径可估算光声直达信号到达A检测点的时间范围。

表2 不同骨组织样本中的声速Table 2 Sound speeds in different bone tissue samples
由表2中的数值模拟仿真结果可以看出,骨组织样本的平均声速为1 600~1 800 m·s-1,结合模拟仿真中所用光斑直径为2 mm,由此可计算出在无衰减情况下,ROI 产生的光声信号传播时间小于1.25 μs。因此,选取A检测点接收到的前1.25 μs内的有效信号作为ROI产生的光声直达信号,如图3(a)中虚线框中选中的信号所示。同时,选取B检测点接收信号的第一个波包作为ROI对应的有效直达信号,如图3(b)所示。
1.5 光声差分衰减频谱
为了求得每块骨组织样本的光声衰减频谱,本文采用差分法,分别计算A和B检测点接收到的直达波的光声功率谱密度,再利用差分法计算骨组织样本的衰减频谱。具体方法如下:(1) 选取A 检测点接收到的前1.25 μs 内的有效信号作为无衰减直达信号;(2) 选取B 检测点接收到的第一个波包作为有衰减直达信号,相比A点的接收信号,在黏滞衰减系数不变的前提下,衰减主要来自于光声传播路径上骨样本微结构引起的散射衰减;(3) 分别计算两个信号的功率谱密度,并计算差分衰减频谱。(4) 根据式(1)计算每块骨头样本在12个角度下衰减频谱衰减系数的平均值及其误差:
其中:αDAS为样本的衰减系数(dB·(Hz·mm)-1);PB(f)为B 检测点接收的光声功率谱密度,PA(f)为A检测点接收的光声功率谱密度;D为B检测点接收到的信号传播距离与A检测点接收到的信号传播距离的差值,数值上等于骨头的直径减去光斑的直径(如图2中所示)。
2 仿真结果与分析
图4 给出了5 块骨组织样本在12 个角度下A、B 检测点接收到有效信号的平均光声功率谱密度。从图4中可以看出:(1) 骨组织样本产生的PA源是宽频带信号;(2) 经骨组织衰减后的信号能量主要集中在低频段,高频时信号衰减严重;(3) 骨质越疏松,经骨组织衰减后的信号保留的高频成分越多。
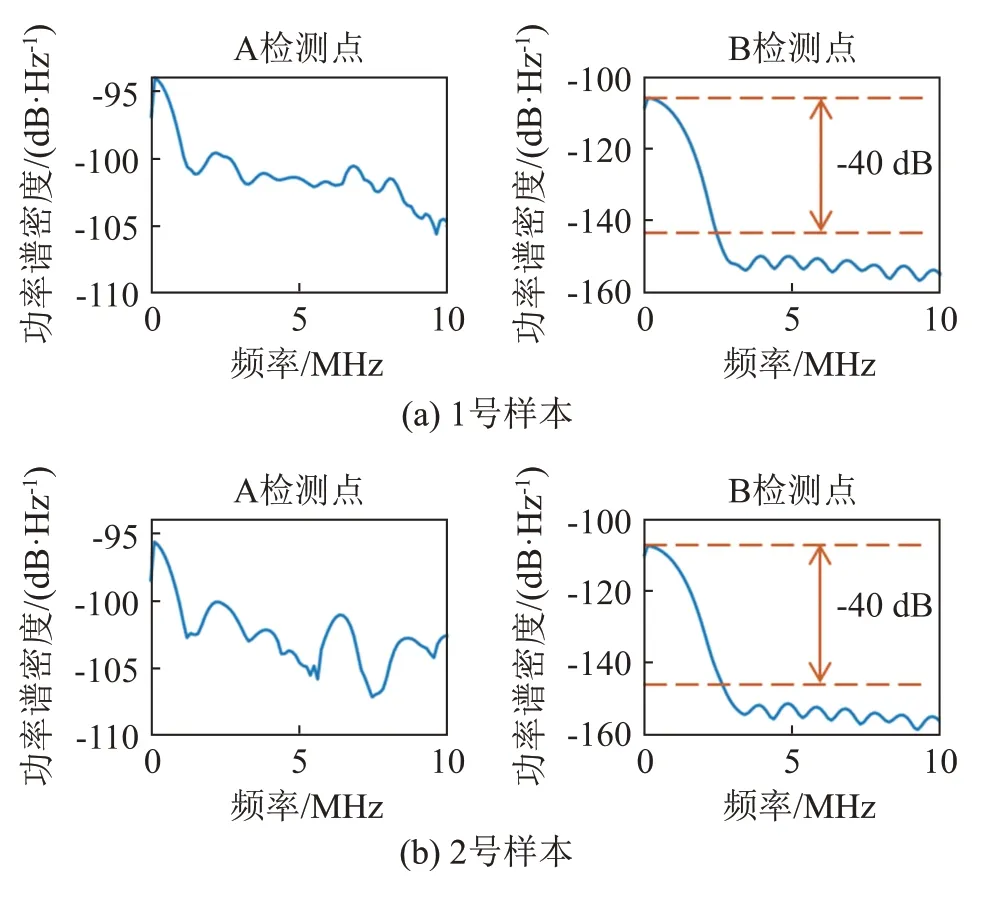
图4 A、B检测点有效信号功率谱Fig.4 Effective signal power spectra measured at the points of A and B of different bone samples
根据式(1)计算的5块骨头样本的差分衰减频谱系数如图5所示。蓝实线为每个样本在12个方向上差分衰减频谱的平均值,并给出了各方向差分衰减频谱的波动范围。由图5可见,差分衰减频谱呈现显著的线性衰减段(linear attenuation band,LAB)和饱和衰减段(saturation attenuation band,SAB)。由于松质骨样本中的声速大约为1 700 m·s-1,光斑直径约为2 mm,骨小梁厚度方向激发的光声信号的最低频率约为0.85 MHz,因此本文将0.85 MHz 作为线性衰减段的初始频率。同时,本文将每块骨组织样本B 检测点的直达信号功率谱由最大值衰减40 dB对应的频率记为该样本的饱和衰减频率(Satu‐ration Attenuation Frequency,SAF),即线性衰减段和饱和衰减段的临界频率。对线性衰减段进行线性拟合,拟合结果如图5(b)所示。


图5 不同骨头样本差分衰减频谱及其拟合图Fig.5 Differential attenuation spectra and their fitting diagrams of different bone samples
通过对比图5中不同骨头样品的光声差分衰减频谱可以分析出:(1) 当孔隙率一定时,光声信号的衰减系数随频率增大,直至达到饱和衰减点,最大衰减系数接近4.5 dB·(Hz·mm)-1;(2) 当孔隙率φ增大时,线性衰减频段的拟合直线斜率随之减小,即线性衰减频段变宽、饱和衰减频率增大。
为了对上述定性结论进行量化分析,进一步提取了每块骨头样本的线性衰减频段的拟合直线斜率和饱和衰减频率作为光声差分衰减频谱的特征参数,分析其与孔隙率的关系。分析结果如表3和图6所示,拟合直线斜率和饱和衰减频率与骨样本的孔隙率均呈强线性相关。因此,有望根据这两个特征参数进行骨质孔隙率的定量评估。

表3 不同骨组织样本衰减特性Table 3 Attenuation characteristics of bone tissue samples

图6 差分衰减频谱拟合曲线中线性衰减段和饱和衰减段与骨样本孔隙率关系的线性回归图Fig.6 The linear regression plots of the relationships of LAB and SAP in the fitting line of the differential attenuation spectra with bone porosity
3 结 论
本文针对PAT中松质骨多孔结构造成的骨质信息提取难点,设计了PAT偏心激励-差分检测系统,以提取差分衰减频谱,从而获取骨微结构信息。利用Matlab k-wave工具包进行数值仿真计算和验证。不同孔隙率骨样本的仿真结果表明:光声差分衰减频谱的线性衰减频段拟合直线斜率和衰减饱和频率这两个特征参数均与孔隙率有强的相关性。因此,基于光声差分衰减频谱的分析方法有望用于骨质定量评估和诊断。

