相关测速声呐模型参数矩阵化求解方法

崔晓康，薛凤杰，赵二亮，王长红

(1.中国科学院声学研究所海洋声学技术中心，北京 100190；2.中国科学院大学，北京 100190；3.北京市海洋声学装备工程技术研究中心，北京 100190)

0 引 言

随着对海洋资源探索的不断深入，潜航设备对测速导航功能的需求和设备所能提供的测速精度都在不断提升。由于传播问题和存在累积误差，全球定位系统和惯性导航都不能满足水下长时间的使用。目前主要的水下测速导航设备是测速声呐。测速声呐包含多普勒测速声呐和相关测速声呐两种，按照不同的原理和功能进行划分，可对应4种不同类型的设备：分别为声相关计程仪(Acoustic Corre‐lation Log,ACL)、声相关流速剖面仪(Acoustic Cor‐relation Current Profiler,ACCP)、声多普勒计程仪(Acoustic Doppler Log,ADL)和声多普勒流速剖面仪(Acoustic Doppler Current Profiler,ADCP)。多普勒测速声呐主要依靠发射声波和散射体之间的多普勒效应来解算载体速度信息[1]；相关测速声呐依靠多个接收阵元接收信号的延时相关性来测量载体速度信息[2]。相对于多普勒测速声呐相关测速声呐具有以下两点优势：(1)相同尺寸的换能器，发射声波频率更低，作用距离更远；(2)声波垂直向下发射，受载体姿态影响较小。但是目前相关测速声呐相对于多普勒测速声呐测速精度较低。一直以来研究人员都在为提升测速精度不断努力。冯雷博士提出了简化的理论相关函数模型，使得参数解算更加简便，便于实时运算[3]；蒯多杰根据修正后的理论相关函数值对最小二乘的目标函数计算公式进行了自适应加权[4]。易卉琴等[5]基于真实数据的相关模型将理论相关函数添加了方向幅值调节因子和旋转因子，使得理论相关函数俯视图形态由圆变为椭圆，更符合实际数据的相关形态。王映春等考虑了阵元坐标误差给测速结果带来的影响，利用相关延时为0 的数据和理论相关函数来估计阵元声中心，进而提高测速精度[6]。文献[7-8]中分析了载体纵横摇对设备测速的影响，并提出了一种目标函数添加权重调节项来提升速度估计精度的方法。本文基于局部最小二乘算法，利用矩阵推导直接求解出目标的解析解，具有无须迭代和运算复杂度低的优点。

1 基本工作原理

波形不变性是声相关技术的基本工作原理。波形不变性原理在常见的流体散射和海底散射等各种声波散射过程中都适用[9-10]。

本文以最简单的一发两收的声呐阵型来阐述相关测速声呐的测速原理。相关测速声呐采用的是宽波束发射换能器，声波以一定的波束角垂直向下发射，以一定间隔连续发射两次信号，对应的发射声波海底散射区域图如图1 所示(图1 中位置1 3 个阵元从右往左分别是发射阵元T、接收阵元R1和R2)。

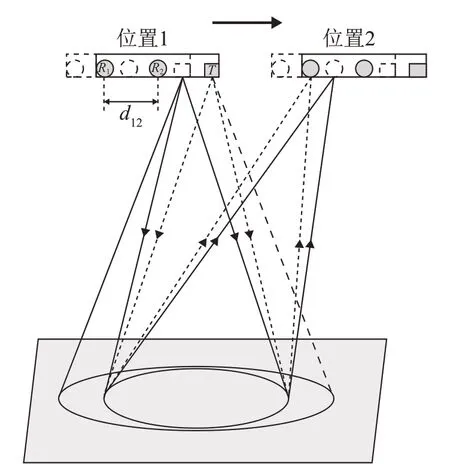
图1 声波在海底散射区域的示意图Fig.1 Schematic diagram of the sound scattering area on the sea floor

当以时间间隔τ发射两次声波，经过相似的传播区域后以时间间隔τ被两个接收阵元接收，此时两个阵元接收的信号具有极大的相似性。根据几何知识可以得出式(1)所示的关系式：

式(1)表明，载体速度V可以通过接收阵元R1和R2构成的矢量d12和两次发射信号的时间间隔τ来确定。

波形不变性原理为载体测速提供了一种求解思路。该原理主要涉及载体相对于散射体的速度、接收阵元构成的空间相关矢量和发射信号相关延时3个参数。通过式(1)将求速度问题转换成了求矢量d12和相关延时τ的问题，矢量和相关延时两个参数如何获得取决于相关测速声呐的设计。有3种比较通用的方法[3]：

(1) 时间相关方法。固定矢量d12，通过相关函数搜索相关延时，然后得到速度信息。

(2) 空间相关方法。固定相关延时τ时，在较多的空间矢量中搜索出适合的矢量d12，进而得到速度信息。

(3) 时空相关方法。通过多种相关延时与阵型设计的多个矢量d12相结合，进而得到速度信息。

通常采用的速度解算方法是空间相关方法，即利用有限的阵元进行特定的布局，利用回波信号构建空间相关矩阵，借助理论相关函数来拟合数据相关矩阵的数据来获取目标函数，最终求取极值来获取水平速度信息。ACL数据处理流程如图2所示。

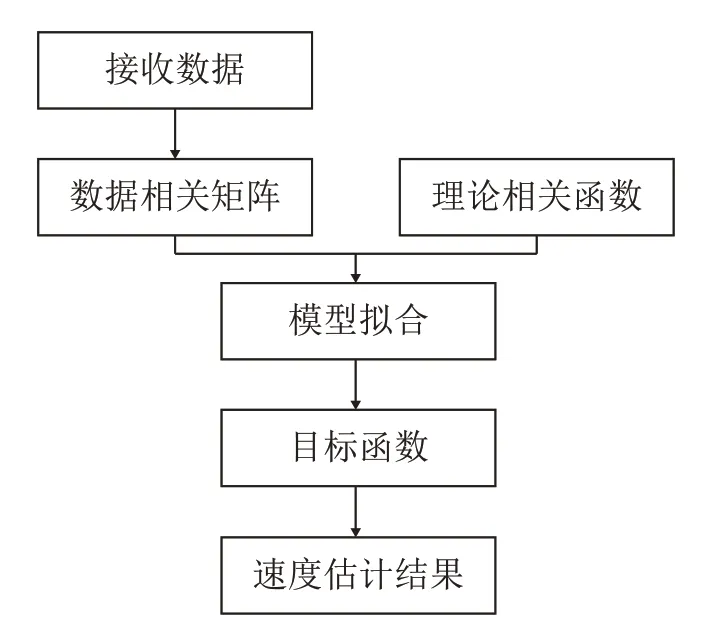
图2 ACL数据处理流程图Fig.2 Flow chart of ACL data processing

理论相关函数的准确性对速度估计结果的精度起着决定性作用。在确定了理论相关函数后，模型拟合的精确程度决定了速度估计结果的精度。

理论相关函数也被称作混响时空相关模型，最早由国外的Dickey 推导给出[2]，国内最早由Zhu等[11]根据Faure，Ol’shevskii 和Middleton 提出的FOM 模型推导建立，随后经过冯雷博士、蒯多杰博士以及易卉琴等研究人员的不断改进后[3-5]，目前采用的理论相关函数为

其中：τ是相关时延，V是三维速度，Φ(τ)是发射信号相关函数，k=ω0/c是波数。

在确定了底回波的理论相关函数后，速度估计方法就是决定性能和精度的关键。目前采用的速度解算方法是以局域最小二乘法为核心的参数分布估计法。该方法采用了水平速度和垂向速度分步估计的思路，利用局域最小二乘法估计水平速度，利用解析方法求解垂向速度，是目前最有效的速度解算方法。

针对以局域最小二乘法为核心的参数估计方法，当局域范围确定后，以最小二乘确定目标函数，搜索使目标函数最小的参数变量。最优参数求解流程如图3所示。

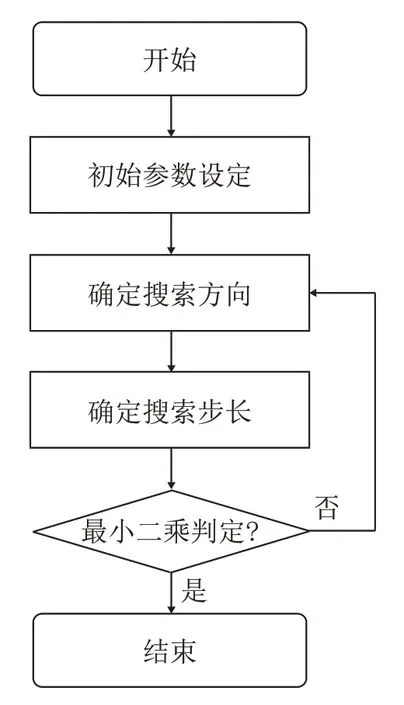
图3 最优参数求解流程图Fig.3 Flow chart of solving optimal parameters

搜索方向和步长采用拟牛顿法，用近似黑塞(Hessian)矩阵来避免Hessian 矩阵求取时的复杂运算。近似Hessian 矩阵采用的是1970 年前后由Broyden、Fletcher、Goldfarb 以及Shanno 提出BFGS算法，具有不用求逆和不用计算二阶导数等优点，在此用Bk代替，Bk的迭代公式为

式中：sk=θk-θk-1，yk=gk-gk-1。sk代表目标参数θk的差值，yk代表一阶梯度gk的差值。根据简化后的近似Hessian矩阵即根据式(3)，不断迭代来获得一定相对偏差Δgk下的目标参数，进而解算出速度信息。

此算法在参数的求解过程中需要多次迭代，参数多，过程复杂，而且需要考虑众多的边界条件限制。为了简化求解流程，降低算法复杂度，本文经过系统的理论推导，提出了基于矩阵推导的模型参数求解方法。

2 基于矩阵推导的模型参数求解方法

基本思路：分离变量使得模型函数可以通过矩阵表示，然后基于最小二乘进行理论推导，最终根据参与运算的数据点直接推导出可以使误差最小的参数，整个过程不需要迭代运算。

基于矩阵的推导方法的目的同迭代方法一样，也是获得最优的模型参数。因此分析还是要基于底回波混响相关模型。目前所采用的底回波模型是经过添加椭圆系数以及旋转角后的模型，模型如式(5)所示。首要目标是把底回波模型中的参数分离，转化为矩阵形式：

对式(5)进行归一化处理后，可得：

为了运算清晰，令x0=2Vxτ，y0=2Vyτ，替换后如式(7)所示：

下面基于式(7)从理论上分析求解最优参数的可行性。首先对式(7)取对数，可得

为了将运算转变为矩阵运算，对式(8)进行变量分离，结果为

式(9)已经完成了变量的分离。下一步将基于式(9)推导最优参数。假如参与拟合的矢量点有N个，则将这N个矢量数据点写成矩阵的形式为A=BC，其中：A为N×1的列向量，其元素为

B为N×6型的矩阵，其行向量为

C为6×1型的列向量：

式中：

N点数据的误差列向量为：E=A-BC，采用最小二乘拟合，使N个数据点的均方误差(Mean Square Erro,MSE)最小，即：

为了简化计算，将矩阵B进行QR分解，即B=QR，分解后Q是一个N×N型的正交矩阵，R是一个N×6型的上三角矩阵，对E=A-BC两边同时乘以QT，推导可得：

误差项为

令：

其中，S为6 维列向量，T为N×6 维列向量，R1为6×6型的上三角矩阵，则式(14)可以进一步转化为

从式(18)很容易可以看出，当S=R1C时，式(14)可以取得最小值，因此只需要求得最小值时的C即可，由S=R1C可得：

根据式(13)以及式(19)得到的结果解线性方程组，即可求得参数x0和y0：

已知x0=2Vxτ、y0=2Vyτ，再根据式(20)即可解算出速度信息。

3 数据验证

3.1 仿真数据验证

通过一个二维旋转高斯模型产生样本数据，将样本数据输入新的模型参数求解方法，根据结果进行验证。

采用的二维高斯旋转模型如式(21)所示。分析结果如表1所示。

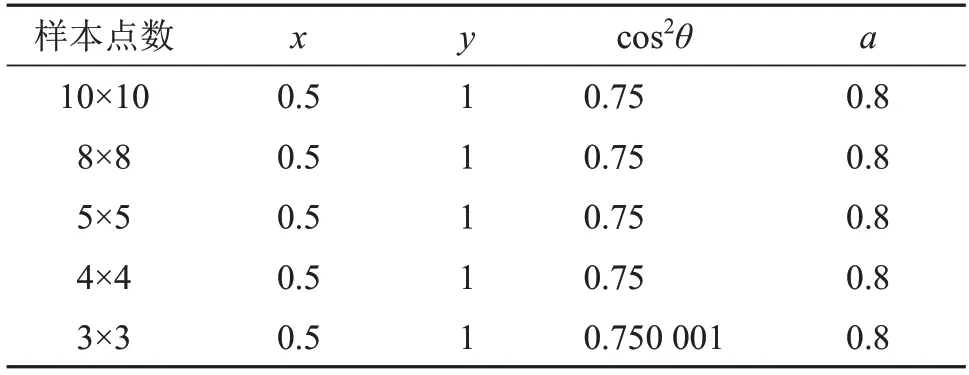
表1 仿真数据验证结果Table 1 Verification results of simulation data

验证方案为固定模型参数，通过改变样本点数，针对不同样本点数得到的结果验证求解方案的可行性。仿真参数设定x0=0.5，y0=1，θ=30°，a=0.8，从中心点向外随机取点，分别在选取样本点为10×10、8×8、5×5、3×3 的情况下进行了测试，运算结果如表1所示。

从表1可以看出，在不同采样点下，仿真测试结果都能正确地解算出目标参数，在没有噪声的情况下偏差基本为0。测试结果验证了基于矩阵推导求解最优参数的可行性。

3.2 实验数据验证

采用湖上试验数据进行结果验证，试验设备为75 kHz声相关计程仪(ACL)，比测设备为GPS(型号为ProPak-G2)，湖况两级左右，测试水域水深65 m左右，各航速情况下的试验数据都在4 200帧左右。矩阵化处理程序和原程序处理结果如表2、3所示。

表2 不同航速下湖试数据的矩阵运算结果Table 2 Matrix calculation results of lake-trial data at different speeds

由于矩阵化运算中舍弃了幅值调节因子，因此所使用的测速范围会有一定程度的下降。速度在7 kn(1 kn=1.852 km·h-1)以上测速偏差明显增大，表2中只列出7 kn及以下航速下的运算结果。

对比表2、表3 中不同航速下湖试数据的矩阵运算和原程序运算的结果可以看出，虽然矩阵运算结果在航速5 kn和7 kn时相对偏差比原程序大，但是偏差方向一致，而且整体测速结果稳定，测速偏差范围在0.2%以内。原程序运算结果在不同航速下偏差有正有负。在测速结果整体一致性上矩阵运算优于原程序求解。

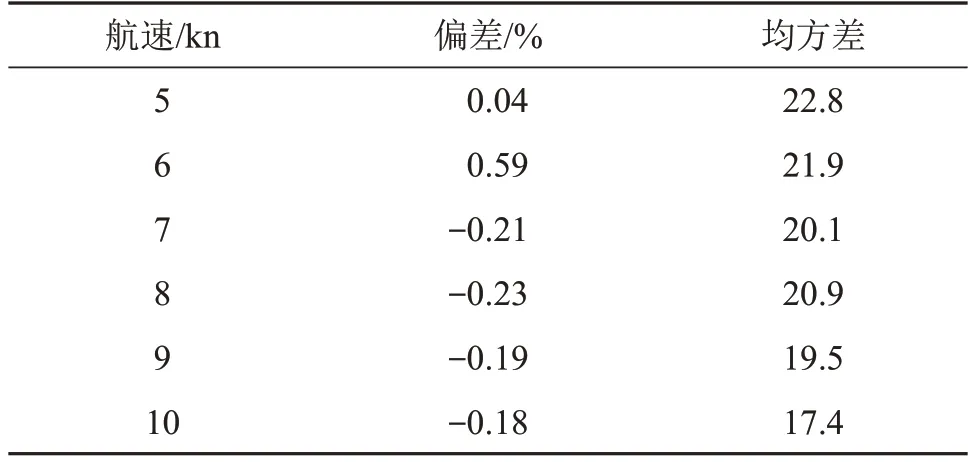
表3 不同航速下湖试数据的原程序处理结果Table 3 Original program processing results of lake-trial data at different speeds

另外，以上运算所使用的样本点数(接收阵元两两之间构成相关矢量，对应的相关值被称为样本点)是基于大量数据验证，是原程序求解方法最优的选择。考虑到矩阵求解法舍弃了幅值调节因子，造成一部分样本点的模型失配，对此采取了减少样本点和增加样本点的尝试。减少样本点是尽量利用满足模型的样本点进行运算。增加样本点是在样本点不足的情况下，样本点新增和带来的模型失配之间会有一个最佳样本点数，使得测速取得最优结果。通过大量的数据验证，本文获得了以下经验结果：

(1) 基于式(1)可以看出，测速范围与相关延时和相关矢量相关，阵元布局决定了相关矢量，当相关延时加倍时，测速范围就会减半，也就是说相同的相关矢量数量，所能表示的测速范围降低为原来的一半，这样会使得同样速度范围内可以利用的样本点数增多，因此通过将相关延时更改为2τ来使相关运算的衰减速度降低，增加可以利用的相关点数；

(2) 原程序是在原模型下进行运算，在12个样本点时结果最优。而本文基于矩阵运算的方法，对使用的模型进行了一定调整，因此需要通过调整参与运算的样本点数来搜索更适合矩阵运算的样本点数。通过对比不同点数下的测速结果，发现2τ延时下采用15点做速度解算得到的测速结果最优(速度小于7 kn)，而且测速均方差也降低到原来的70%左右。另一方面，对航速7～10 kn情况也针对不同点数做了进一步分析。发现当参与相关运算的点数为13 时测速结果稳定。不同速度下的矩阵运算测速结果如表4所示。整体偏差方向一致，不同速度下的相对偏差在0.3%以内。以上结果进一步验证了矩阵化求解算法的可行性。

4 结 论

本文通过理论分析得到了基于矩阵推导的最优参数的解析解，并通过仿真验证和湖上试验数据，验证了该方案作为一种速度解算方法的可行性。另外通过对时间复杂度分析，原程序由于需要求逆运算和多次迭代，时间复杂度为M×N3量级，其中M代表迭代运算次数。基于矩阵推导的运算方法虽然也涉及矩阵求逆，但是为上三角矩阵求逆，整体时间复杂度为N2量级，其中乘法运算和加法运算次数相当。因此，基于矩阵推导的最优参数求解方法相较于基于拟牛顿法的迭代参数求解，在时间复杂度上具有一定的优势。

本文由于无法应用幅值调节因子，因此带来了一定的模型失配问题，导致文中所提测速方案没有达到最优的测速结果。后续研究将考虑从提升可以利用的样本点数和提高矩阵推导算法的容错性两方面进一步深入研究，以获得更加精确的估计参数。