面向跨水空介质通信的雷达水表面声波提取

符晓磊，夏伟杰，董诗琦

(南京航空航天大学电子信息工程学院，江苏南京 211106)

0 引 言

随着技术的进步和对资源需求的快速增长，人们将目光投向了广阔的大海，对海洋的勘探活动日益增多。海洋不仅仅蕴藏着重要的物质资源，同样也是我国重要的战略资源，现代战争是科技战、信息战，拥有尖端的海洋军事科技往往可以掌握作战的主导权。如何快速灵活有效地进行跨水空介质通信对于海洋资源的勘探和海上作战都非常重要。

水下通信网络都面临着同一个问题：无法直接地跨水空介质通信。这是因为目前主流的无线信号载体在水空介质中传播特性差异很大[1]，例如电磁波由于海水较高的传导损耗在水中迅速衰减，而声波入射水空界面后几乎全部的能量都被反射回水中。因此水声技术仍然是实现水下目标探测、水下航器通信的主流技术手段[2-3]。如今较为先进的水空通信网络依赖于自主式水下航行器潜入水下采集数据再浮上水面发送数据[4]，整个过程耗时长、成本高，且隐蔽性差，存在军事应用方面的安全隐患[5]。在水面部署中继器也是一种常见的方法[6]，但其部署位置相对固定，灵活性较差。有学者还提出了基于蓝绿光的水下通信[7]，蓝绿光在海水中衰减较小，最大穿透度为600 m，为实现高速率通信提供了可能，但光在水中的传输环境复杂恶劣且需要高精度对准，同时海面的波动会使光束产生扩散和偏移，引起光信号的能量衰减甚至通信中断。

当水下声源产生的声信号传播到水空边界时，水表面将产生沿水面横向传播的微幅波，该波动携带着水下声源的频率信息，很多学者称其为水表面声波(Water Surface Acoustic Wave，WSAW)[8]。由于WSAW的振幅很小，无法通过常规的方法提取，有学者提出了水表面声波的激光相干探测[9-10]，同时激光能量密度很高，照射水面将产生激光声[11]，为水空的下行通信链路提供了一种新思路。麻省理工学院实验室首次提出了一种跨介质通信系统[12]，采用雷达提取WSAW信号以实现跨介质通信。

本文提出了一种基于级联成像调频连续波(Fre‐quency Modulated Continuous Wave,FMCW)雷达提取WASW 信号的新方法，利用FMCW 雷达[13]获得水表面波信息，再通过相关的信号处理提取出携带声源信息的WSAW 信号并结合匹配滤波技术提高输出信噪比[14]。在该方法中，信号仍是以声信号的形式抵达水面，能量损失相对其他形式的信号小；再通过雷达以非接触的方式探测水面微幅波的信息，解决了隐蔽性差的问题，也避免了蓝绿光需要高精度对准的问题，雷达只需要位于被声源激励的水面上方即可提取蕴含水下声源信息的WSAW 信号。由于WSAW 相对于水面自然扰动十分微弱，基于FMCW 雷达的WSAW 的提取非常具有挑战性。考虑到其在军事上的应用，这也是一项非常具有研究价值的工作。

1 基于FMCW 雷达的WSAW 信号提取原理

当水下声源产生的声波传播到水空边界时，由于空气相对于水来说是一种绝对软介质，水表面将产生与声波频率一致的振动，我们称其为水表面声波(WSAW)。雷达目标通常在主体运动的同时还伴随着部分感兴趣目标的微动，例如导弹的进动、直升机螺旋桨的转动、发动机的振动、人体的肢体摆动及呼吸心跳等[15-17]，这些微小运动会对雷达回波产生相位调制，使得目标主体运动产生的多普勒频率发生一定的频偏，这种效应称为微多普勒效应。水表面波由WSAW 和自然扰动两部分构成，也是一种微动信号。本文考虑的自然扰动为厘米级，幅度相对其他微动较小，所以主要考虑水表面波对雷达回波的相位调制。雷达提取水表面声波系统的示意图如图1所示。

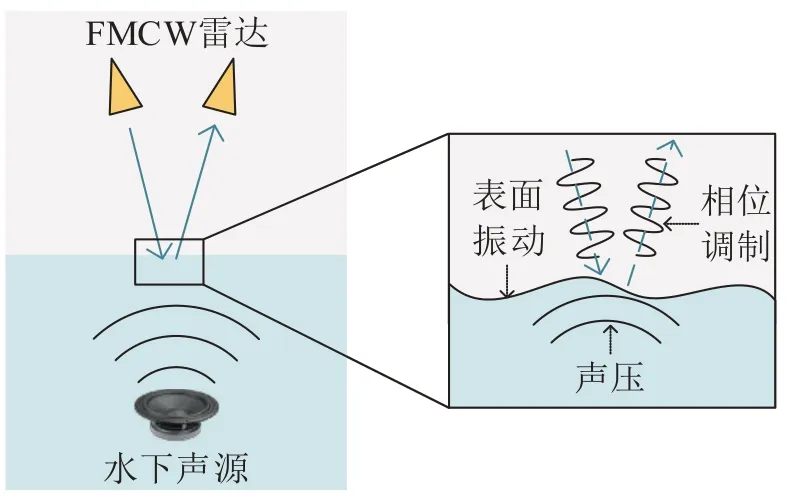
图1 雷达提取水表面声波系统示意图Fig.1 Schematic diagram of radar system for extracting WSAW

WSAW 信号包含在雷达回波的相位信息中，如何提取和处理并检测蕴含着水下声源信息的WSAW 信号是本文的重点。图2 为基于FMCW 雷达的WSAW 信号提取处理流程图。本节主要讨论了水面相对平静时的WSAW 信号的提取原理，考虑将多通道中频信号sn处理为多角度原始相位ϕBm，由于水面扰动较小，中央波束对应的原始相位经带通滤波即可获得有效的WSAW信号。

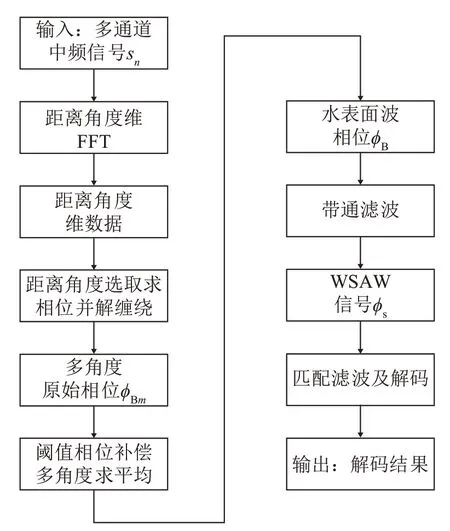
图2 WSAW信号提取处理流程图Fig.2 Flow chart of WSAW signal extraction

1.1 水下声源激励水表面声波的理论模型

声波传播到水空边界时将发生反射与折射的现象，满足声压连续性条件，即：

式中：pi(r，t)为入射声压，pr(r，t)为反射声压，pt(r，t)为透射声压。水空边界的声反射系数R和折射系数D为

式中：ρ1c1为水介质的声阻抗，ρ2c2为空气介质的声阻抗，分别约为1.56×106kg·(m2s)-1，404.5 kg·(m2s)-1。考虑声波垂直入射水面的情况，由式(2)可知，透射到空气中的声波非常微弱，可以忽略不计，入射声压pi近似等于反射声压pr。利用声阻抗的定义公式并结合入射声压和反射声压的关系，可得该处质点的运动速度的大小vs：

设质点的角频率为ωs，则可推导[9]出该质点的振动幅度As为

由式(4)可以看出，振动幅度与入射声压成正比，与质点振动频率成反比。文献[8]中的研究表明：水下声源激励的WSAW 中仅有与声源频率一致的波动才会有显著振幅，所以WSAW 将携带水下声源的相关信息，为后续的雷达提取水面微动信号提供理论基础。由于声波引起的质点振幅相对其波长极小，可以用线性小振幅波理论来进行建模研究，根据该理论的相关推导[9]，水表面声波的二维波幅方程为

式中：x为水面切向坐标，ks为水表面波的波数，ωs为水表面波的角频率。水表面声波的恢复力主要由表面张力和重力构成[9]，其波长的色散关系可表示为

式中：σ为水的表面张力，g为重力加速度。由于水介质的黏滞性，随着距离的传播，水表面声波的幅度也会逐渐衰减。

在很多雷达系统中，通过发射如式(7)所示的线性调频信号，使得回波在经过脉冲压缩后有更高的增益。同样的，水下声源也可以采取以上方案，以获得更高的增益，使信号更容易被检测。所以将水下声源的发射信号SaT(t)进行如下调制：

式中：fs0为起始频率，μs为调频斜率，Ts为信号周期。采用时频分析[18]的方法可以更精确地分析线性调频信号，在本文中采用了短时傅里叶变换(Short-Time Fourier Transform,STFT)，该变换是在给定信号上加滑动窗并做傅里叶变换以得到信号在不同时刻的频率信息。STFT的计算公式为

式中：s为信号，g为窗函数，*表示共轭。

水表面波包含自然扰动和WSAW 两部分。由于式(4)以及水介质黏滞性导致的横向衰减，声源引起的质点振幅As(t)将会随着线性调频信号频率的升高而减小；假设自然扰动的频率为fn，振幅为An，则水表面波R(t)表达式为

式中：ϕs、ϕn分别为WSAW 与自然扰动的初始相位。根据式(4)，由于声源功率限制，WSAW 的振幅通常无法达到厘米级，同时受限于雷达测距的精度(1 μm)，在实验中控制声源功率和声源到水面的距离，保证WSAW的幅度在微米量级。

水下目标噪声谱通常是比较复杂的，在提取WSAW 信号时避免其干扰非常重要。由于水下目标噪声在水面产生的声压远小于实验中的水下声源产生的声压，如文献[9]中列举的某型常规动力潜艇在高航速的条件下引起的水面微幅波中心幅度仅为63 nm，所以一般的水下目标噪声在水面引起的振动对WSAW 信号的干扰可以忽略。此外，由于WSAW 幅度极小，且与幅度相差千倍的自然扰动叠加，虽然两者频率相差较大，可以通过频域滤波分离，但常规手段无法有效提取WSAW。本文提出了一种基于FMCW雷达的水面微动提取方法。

1.2 FMCW雷达微动信号提取

FMCW 雷达通过发射连续线性调频信号来感知目标的位置信息。FMCW 雷达微动信号提取本质上是对含有目标距离信息的差拍信号进行频率与初始相位的估计。

FMCW雷达的发射接收信号如图3所示。图3中，fmin=f0-(B/2)是起始频率，T是调频周期，f0是中心频率，B是调频带宽，调频斜率μ=B/T，τ为接收信号延时。发射信号ST(t)的表达式为

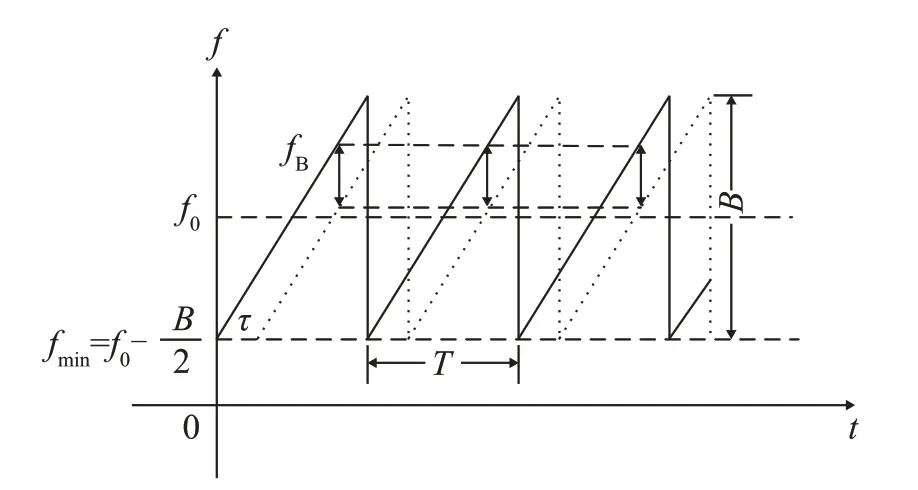
图3 线性调频信号参数图Fig.3 Parameter illustration of a linear FM signal

接收信号经过混频，滤除高频分量并忽略相关小量可以得到基带差拍信号sB(t)：

式中：fB为与距离相关的差频，ϕB为差拍信号的初始相位，R表示目标距离。

以下图4～16 中的信号处理相关的结果均是实测数据处理所得。如图4所示，差拍信号为距离相关的单频信号，对其做距离维FFT，图中的黄线即为水面所在距离门。由此可知水面到雷达的距离为1.42 m，WSAW的振动信息包含在此距离门的相位ϕB(t)中，令R=R0+R(t)，将式(9)代入，则ϕB(t)的表达式为

图4 用于测距的差拍信号FFT结果Fig.4 FFT result of beat signal for ranging

式中：λ为雷达的工作波长，R0为雷达到水面的距离(不含微动信息)，ϕB(t)中包含自然扰动ϕn(t)和WSAW相位ϕs(t)两部分。

由于自然扰动和WSAW的振动幅度相差很大，相差约103的数量级。这就限制了对于FMCW雷达波长的选择，一方面因为WSAW的幅度为微米级，要使这个量级的振动有效地反映在相位中，雷达波长应该选得更小；同时，相较于厘米级的水面自然扰动，若选择雷达的波长过小、频率过大(如THz)，将导致相位变化过快，无法有效跟踪水面位移。因此在雷达提取水表面声波的系统中，选用了频率为77 GHz的FMCW雷达，其波长为3.9 mm，相对符合上述要求。自然扰动的振幅An和WSAW的振幅As虽然相差悬殊，但其在频率上区别明显，可以通过带通滤波将WSAW 信号分离出来，进一步分析其频率特性。

除了幅度相差悬殊，自然扰动还会使回波的雷达散射截面(Radar Cross Section,RCS)剧烈起伏，影响WSAW 信号的提取。所以选用了阵列FMCW雷达进行波束形成[19]，对多个相位中心的数据进行联合相干处理，实现空间上的选择性接收，即形成天线波束指向所期望的方向。

考虑窄带平面波入射一维均匀直线阵，示意图如图5所示。入射信号形式为sn(t)，阵元信号的矢量形式s如式(14)所示：

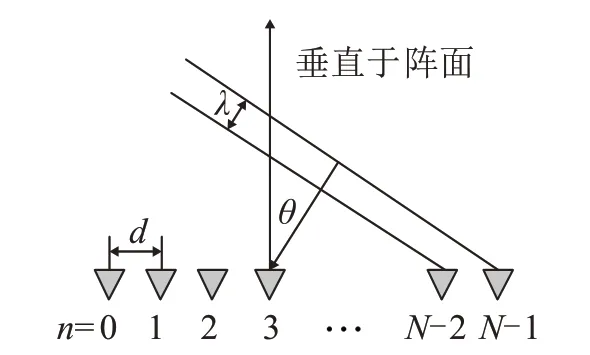
图5 均匀直线阵示意图Fig.5 Schematic diagram of a uniform linear array

常规的非自适应波束形成为阵元信号的加权求和，可以通过对sn序列进行FFT 快速实现，求得S(m)的表达式为

式中：m为波束号，M为角度维FFT 的点数，ϕ=dsinθ/λ-m/N，公式后半部分为sinc 函数，m号波束对应波束角度θm，所以S(m)对应的波束指向为ϕ=0 即θm=arcsin[(mλ)/(Nd)]处，该波束求得的相位为ϕBm。

FMCW 雷达经过差频后获得多通道中频信号sn，再通过距离-角度维FFT 处理得到水面的距离-角度维数据，各点数据幅值相对于其中的最大值进行归一化，以下同。选取水面所处距离门中绝对值最大的波束，该波束即为垂直水面的回波方向，我们称其为中央波束ϕBM。对应水平摆放的雷达来说，中央波束即是θM=0处。图6为水平放置FMCW雷达处理得到的距离角度分布图，雷达摆放稍有倾斜，所以中央波束对应角度为2.2°。

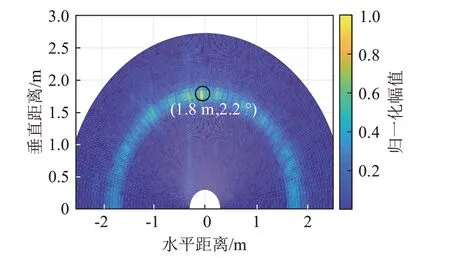
图6 雷达水平放置时测量的距离角度分布Fig.6 Distance and angle distribution measured when the radar is in horizontal placement

平静水面的WSAW信号提取结果如图7所示。在选取合适的距离-角度维数据后，可以采用相位反正切法求解相位，获得多角度的原始相位ϕBm，但该方法求得的相位被限制在[ -π，π]中，导致相位的测量值与实际不同。如图7(a)所示，若ϕBm中的某些值超出这个范围则会出现相位缠绕的现象，即超出该范围的值会被加上或减去q×2π，使其落在这个区间内。要恢复出实际值，就需要确定q的值。本文采用一种判断相邻采样点的相位差值大小的方法来进行解缠绕。假设缠绕的相位为ϕ*Bm，相邻两个采样点的真实相位的最大差值小于π，则解缠绕的公式为

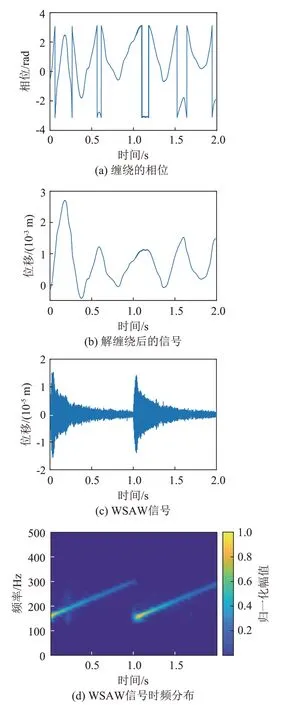
图7 平静水面提取的WSAW信号波形及其时频谱Fig.7 WSAW signal waveform and its spectrogram extracted under calm water surface

式中：n为不小于2 的整数，Δϕm(n)为m号波束角度对应的第n个时间采样点相位的真实值与测量值的差值，初始值Δϕm(1)为0。所以解缠绕后相位ϕBm为

解缠绕的效果如图7(b)所示，可以观察到自然扰动的波高约为1.5 mm，解缠绕后的相位如式(12)所示，为WSAW 与自然扰动的叠加，当自然扰动不大时，选取一个角度即中央波束ϕBM即可获取有效的原始相位ϕB。

实验中声信号的起始频率fs0=150 Hz，信号长度T=1 s，调频斜率μs=150 Hz·s-1，带宽B=150 Hz，采样频率fs=1 840 Hz。WSAW 信号频率为150～300 Hz，而自然扰动一般来说频率为0.5～2 Hz，两者可以通过滤波很好地区分，图7(c)为滤波后的WSAW 的时域波形，WSAW 信号的平均幅度约为6 μm，图7(d)为WSAW的时频分布，各个时间-距离点的幅度相对于其中的最大幅度进行归一化，以下同。可以明显看到线性调频信号在时频图上的亮斜线，实验说明在水面平静的情况下，使用带通滤波器能直接分离得到WSAW 信号的ϕs并通过时频分析观察其调频特性。

利用如图2中所示的流程图，在水面相对平静的环境下，可以使用相对简单的方法判断水下声源信号的有无。但当水面自然扰动较大时，会出现RCS剧烈起伏、相位跳变的问题，第2节将详细讨论该情况下的信号处理方法。

2 基于FMCW 雷达的WSAW 信号处理方法

与水面平静的情况不同，水面自然扰动过大会造成RCS 剧烈起伏、相位跳变的问题，针对该问题，本文提出了一种多角度积累结合阈值相位补偿的方法，从而获取有效的原始相位ϕB，并通过滤波分离出WSAW 信号，最后通过匹配滤波和解码确定水下声源的状态。

大幅度自然扰动下的雷达回波信号与微扰情况有一个很大的区别：RCS起伏很大，RCS最小处仅为最大值的0.3%，在厘米级自然扰动下就会出现上述问题。图8(a)为我们制造的机械扰动的原始相位，可以得出该自然扰动的波高为1.4 cm左右。在图8(b)中的距离-时间分布上能看到水面所在距离门的信号幅值变化剧烈。在RCS极小值求得的相位是值大于π 的相位加上或减去q×2π，将跳变量限制在[ -π，π]随机分布的，解缠绕将相邻时刻跳变绝对在[0，π]内。图8(c)展示了局部的归一化RCS 与差分相位的对比，可以看到RCS较小处，求得相位差分的绝对值较大但小于π，符合上述推测。

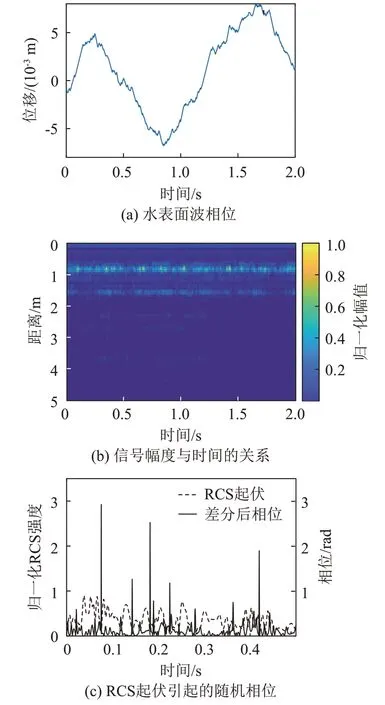
图8 大幅度自然水面扰动对WSAW信号提取的影响Fig.8 Influence of large-scale natural water disturbance onWSAW signal extraction

由于随机相位比真实相位变化大得多，ϕBM经过带通滤波后真实信号被淹没，如图9(a)、9(b)所示，滤波后信号的WSAW 被随机相位淹没，时域上存在幅度很大的干扰，所以在其时频分布中难以辨认线性调频特性。针对随机跳变的相位，提出了一种阈值相位补偿算法减小其影响，其主要思路是将判定为相位随机跳变的点修正到与前两个点的趋势相同，公式为

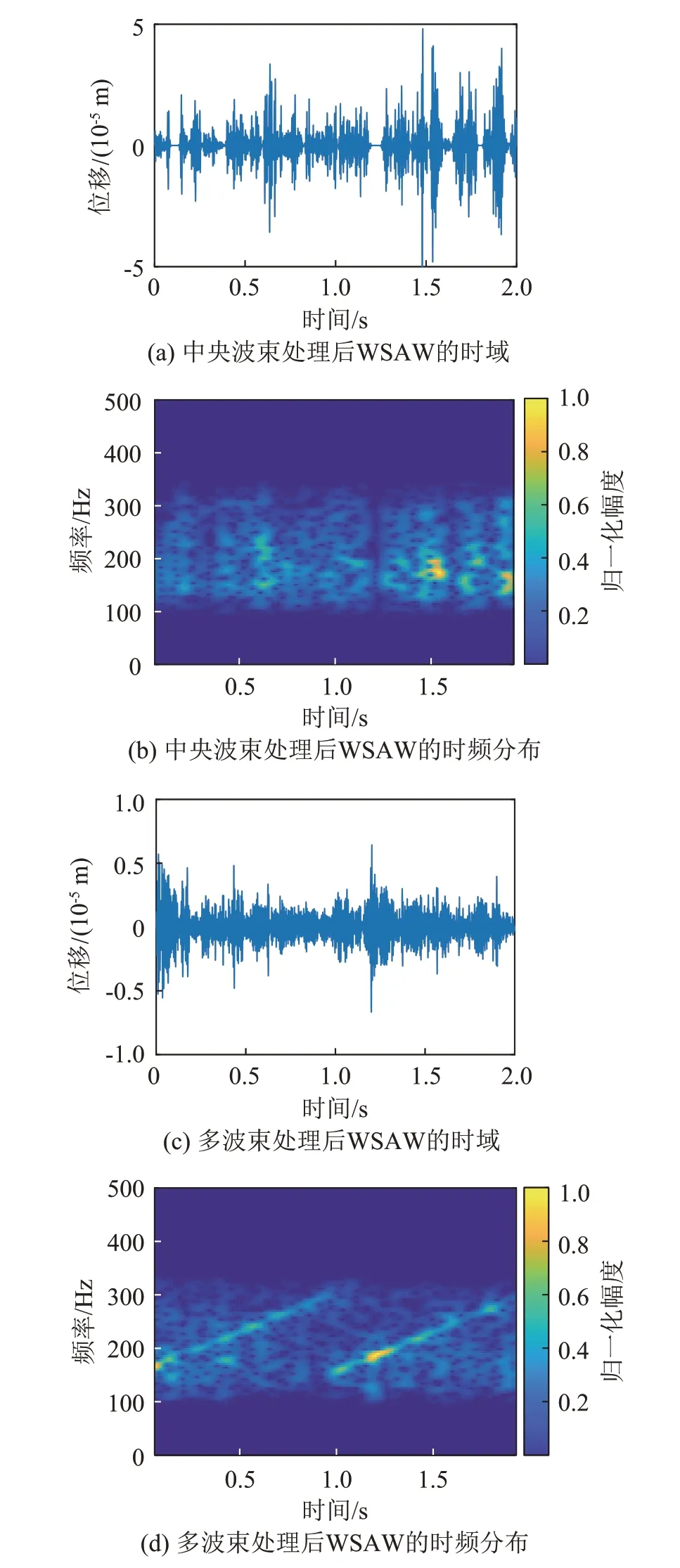
图9 WSAW信号经多角度积累结合阈值相位补偿处理和仅中央波束处理的结果对比Fig.9 Comparison of WSAW signal processing results by multiangle accumulation combined with threshold phase compensation and by only central beam processing

式中：ϕBm为m号波束的原始相位，ϕΔm为相位修正量，ϕT为判断相位是否跳变的相位差阈值，通过测试对比将ϕT设为π/20。将ϕΔm与ϕBm相加即可得到与阈值补偿后相位ϕ′Bm：

如图2流程图所示，经过1.2节中的距离-角度维FFT与距离门选取、求相位解缠绕操作后，将得到M个角度的原始相位数据ϕBm，由于RCS起伏引起的相位随机跳变问题，需要通过上述的阈值相位补偿算法减小其影响，得到补偿后相位ϕ′Bm。最后选取中央波束附近2l+1 个波束的相位求平均得到水表面波相位ϕB，即多角度积累，以提升输出信噪比(Signal to Noise Ratio,SNR)。假设中央波束对应的相位为ϕ′BMc，水表面波相位ϕB计算公式为

式中：Mc为中央波束对应波束号。考虑到不同角度对应的水面处，声信号存在不同的时延，但由于水声信号频率较小(小于300 Hz)，其波长较长，所以进行多角度积累时如果l取得较小，可以保证所积累的角度对应水面处于同一距离门，同时角度范围内的声信号时延导致的相位差可以忽略，各角度处理得到的WSAW 信号的相位一致，积累后可以提高输出信噪比。经过多角度积累和阈值相位补偿后得到有效的水表面波相位ϕB，再对其进行带通滤波即可得到WSAW信号ϕs，如图9(c)、9(d)所示，时域中相位跳变引起的大幅度干扰信号减弱，从时频分布中可以清晰看到亮斜线。多角度积累和阈值相位补偿实质上是为了降低相位随机跳变产生的影响，上述对比表明，在较大自然扰动下(幅度为1.5 cm 左右)，该算法可以较好地提取WSAW 信号并分析其调频特性。

线性调频信号能够通过线性频率调制来获得更大的时宽带宽积，水下声源发射信号SaT(t)如式(7)所示，带宽为B=μsTs，D=BTs被称为脉宽压缩比，等于信号的时宽带宽积。根据脉冲压缩理论可知，经匹配滤波后信号的输出信噪比为输入信噪比的D倍。根据实验中的声源参数计算出D=150，脉冲压缩前后的SNR 增益为21.76 dB。对图9(b)中的WSAW 相位ϕs进行匹配滤波，匹配滤波结果如图10 所示，计算得到输入信号ϕs的SNR 为5.23 dB，匹配滤波后输出SNR 为23.09 dB，SNR 增益为17.85 dB，考虑到ϕs各频率幅度不恒定，增益将有所降低，匹配滤波的增益与理论基本相符。图10中的纵轴归一化幅度为匹配滤波结果相对其最大输出幅度进行归一化所得，以下同。

图10 WSAW匹配滤波的结果Fig.10 Result of WSAW matched filtering

3 实验分析与讨论

3.1 实验场景及仪器

实验采用的级联成像FMCW 雷达设备是TI 公司的TIDEP-01012，由4片AWR2243级联设计，支持76～81 GHz 的频带范围。实验中采用12 发、16收的天线阵列以时分复用的多输入多输出(Multiple Input Multiple Output,MIMO)方式构成86个通道一维虚拟天线阵列。水下声源为UWS-015 水下扬声器，额定功率为20 W，频率范围为80～20 000 Hz。

为了评估上述方法的有效性，在湖边展开了一系列实验，实验场景如图11(a)所示，级联成像FMCW雷达位于水面上方1.7 m处，声源位于距水面0.5 m 的水下。根据式(12)采用雷达测量水面振动，发现由风引起的水面自然扰动幅度在毫米量级，此时的WSAW 信号只需将中央波束的相位经过带通滤波即可获得。通过制造机械扰动形成厘米级的波浪，测试该情形下的WSAW 信号提取处理效果。在雷达倾斜测量的实验中，由于需要控制水面波动幅度稳定，选择在室内进行实验测试，实验场景如图11(b)所示，声源放置在水盆中，声源距水面0.3 m左右，FMCW雷达架设在水面上方0.9 m处，通过相对恒定的风驱动水面以获得幅度较为稳定的水面波动。

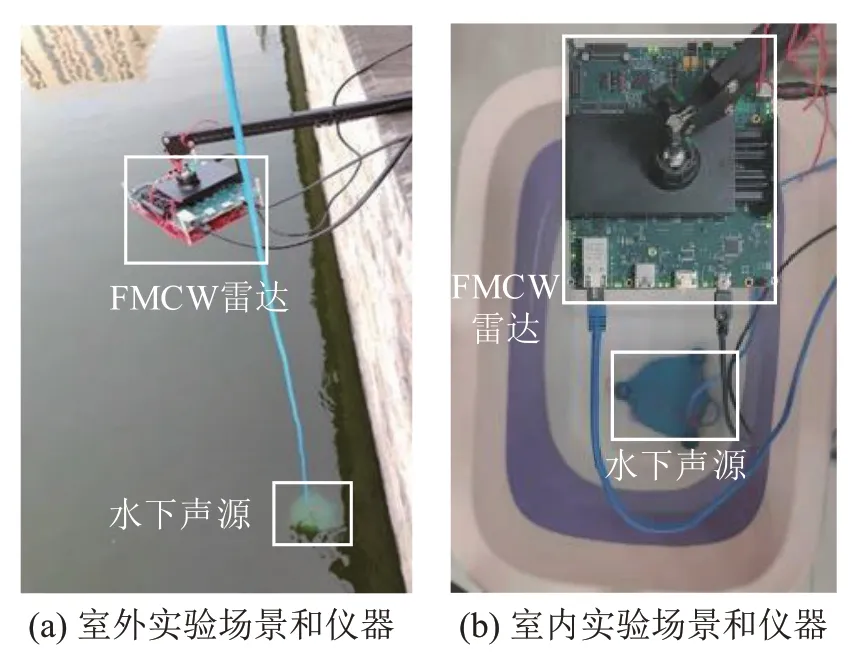
图11 实验场景及仪器Fig.11 Experimental scene and instruments

3.2 不同扰动下的实验结果对比与解码结果

在FMCW雷达提取WSAW信号的过程中，将不可避免地受到水面自然扰动的影响，由于声源激励的WSAW 信号幅度十分微小，不同扰动下处理得到的WSAW信号SNR明显不同。为了评估自然扰动对通信系统的影响，在湖边通过机械摆动生成频率为1～3 Hz 的扰动并控制其扰动波高，提取不同扰动波高时的WSAW 信号并估计其SNR，将得到的实测数据绘制成折线图，如图12 所示。实验结果表明，随着扰动波高的增大，提取到WSAW信号的SNR 逐渐减小，各幅度扰动下匹配滤波的平均增益为18.1 dB，与2.2节中的增益很接近，相对符合匹配滤波的理论增益。

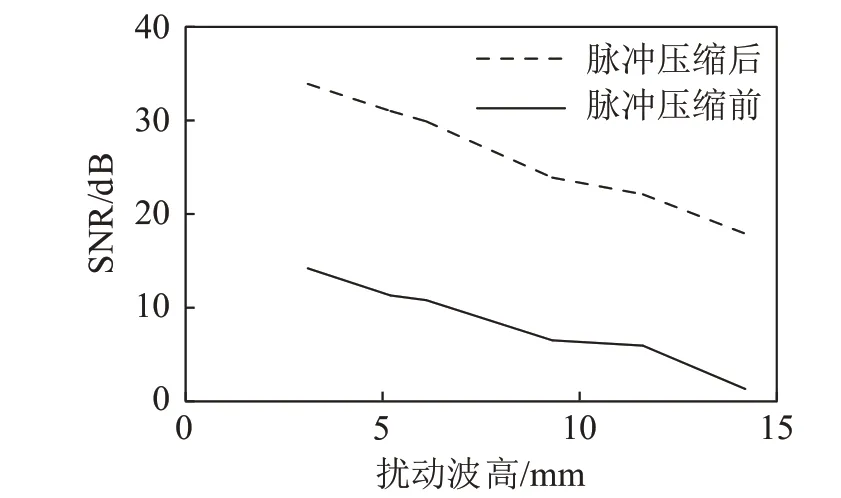
图12 不同波高下WSAW信号的SNRFig.12 SNRs of WSAW signal at different wave heights

编码部分采用振幅键控(Amplitude Shift Key‐ing,ASK)调制，即水下声源发送LFM 信号为“1”，不发送信号为“0”，码字长度为1 s，处理得到WSAW信号的时频分布如图13(a)所示，可以比较明显地看到时频分布上发送LFM 信号时的亮斜线，从图13(b)上可以发现匹配滤波后的输出信噪比更高，可以通过门限设置来判断信号的有无，从而实现对水下信号的解码。实验表明在较大的自然扰动下可以有效地提取出WSAW 信号并实现正确解码。

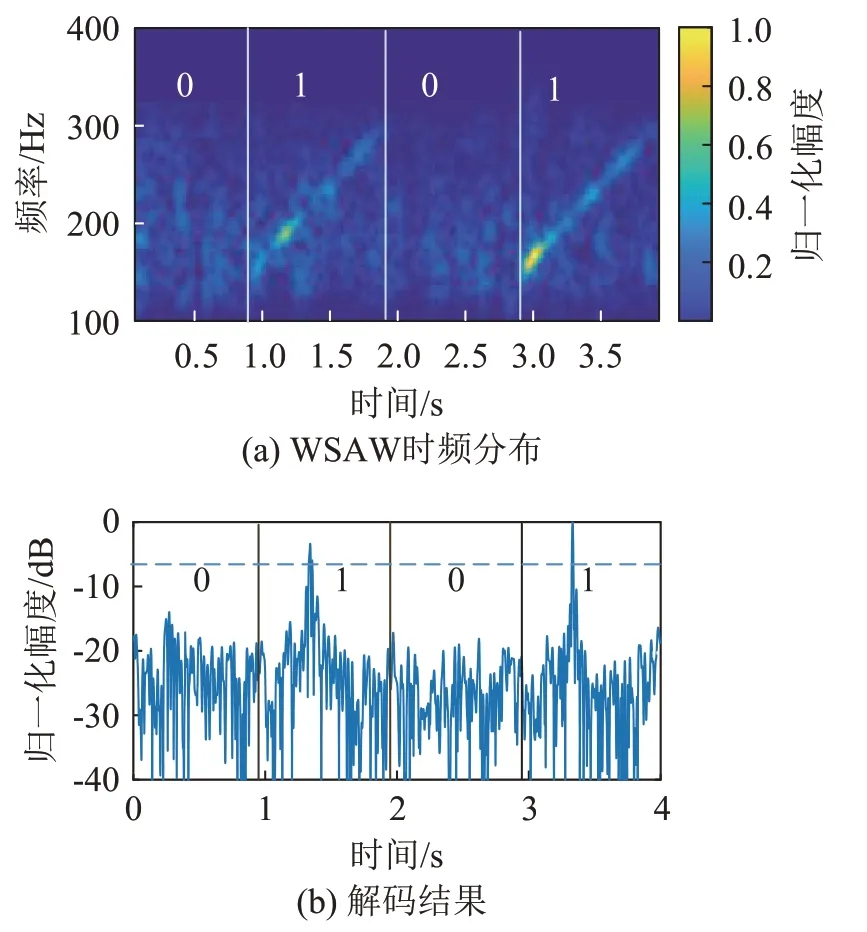
图13 WSAW信号的时频分布及其相应的ASK调制解码结果Fig.13 Spectrogram of WSAW signal and its decoding results of the corresponding ASK modulation

3.3 雷达倾斜情况的实验结果

对于WSAW信号的提取，文献[9-10]中提出了基于激光干涉的微弱振动信号提取方法，该方法的测距精度很高，但也存在着一些问题，比如激光需要严格垂直水面并对准水下声源。本文采用的级联成像FMCW 雷达在与水面呈一定倾角时仍能提取WSAW信号。为了验证雷达倾斜提取WSAW信号的有效性，将雷达架设于水下声源的正上方，其相对于水面的倾斜角约为30°和50°。获得的距离-角度维数据的极坐标形式如图14所示，图中的亮点对应水面所处距离角度单元，计算出两次倾斜的角度分别为31.2°和47.8°，与实际倾斜角度基本相符。

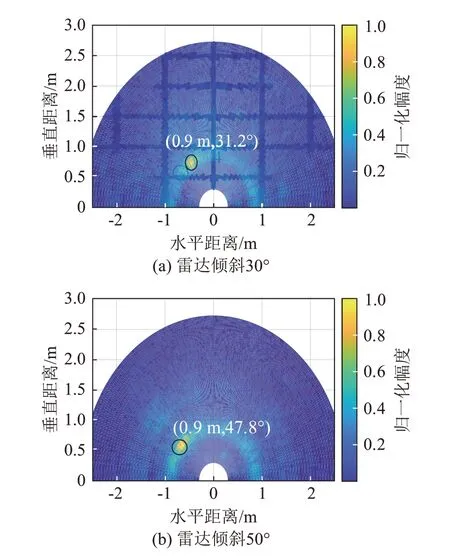
图14 雷达倾斜测量的WSAW信号的角度距离分布Fig.14 Angle-distance distribution of WSAW signal under radar tilt measurement

对倾斜测得的数据进行处理，结果如图15 所示。实验证明：在毫米级的扰动下，雷达倾斜至50°仍能有效地提取WSAW 信号并分析其调频特性，以此实现水下声信号的接收。

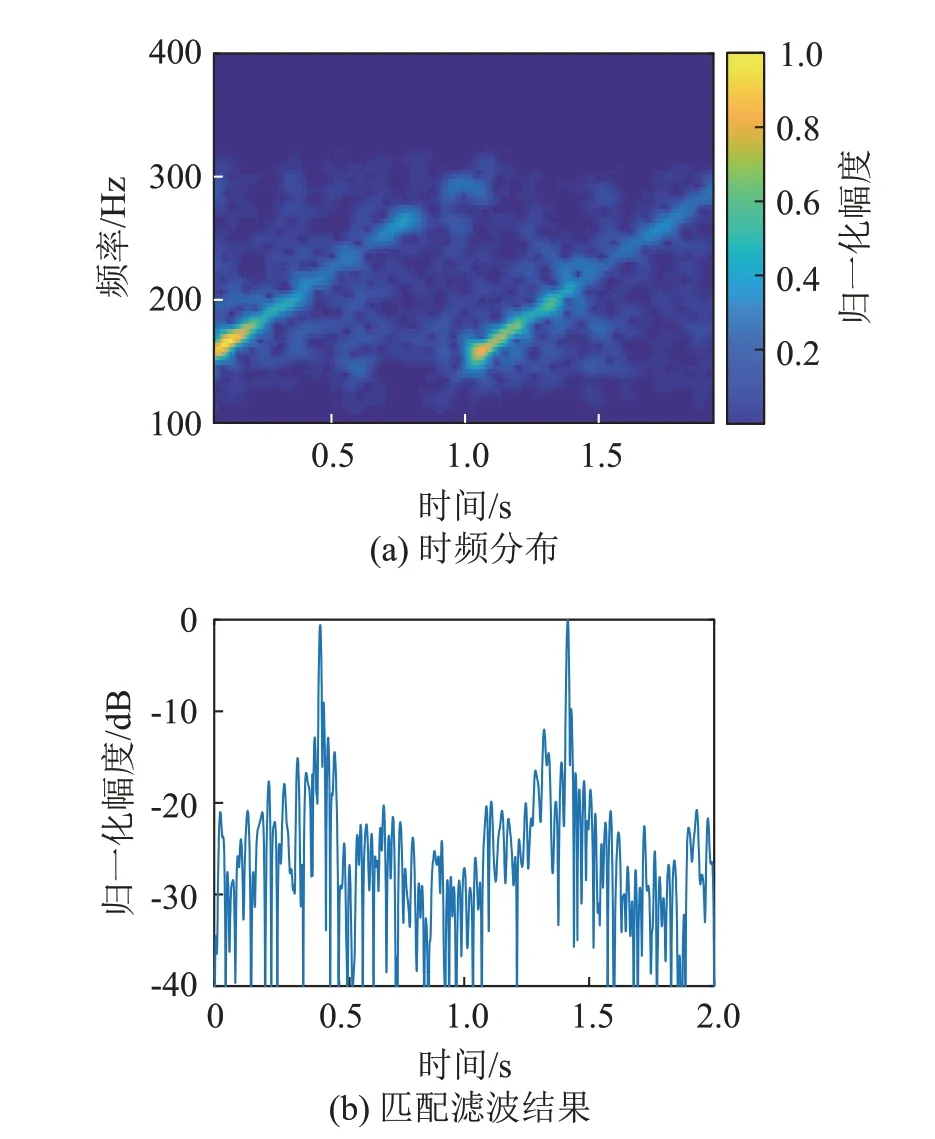
图15 雷达倾斜测量的WSAW信号处理结果Fig.15 WSAW signal processing results under radar tilt measurement

为了进一步评估雷达倾斜角度对WSAW 信号提取效果的影响，将实验场景切换到相对无风的室内，通过相对恒定的风(由风扇产生)来驱动水面产生扰动并用雷达测量其幅度，再调整风扇的风速从而控制水面波动幅度在4 mm左右。逐渐增大雷达倾斜角，对比不同角度下处理得到的WSAW 的信噪比，结果如图16所示。由图16可以看出，由于实验过程中每次实验的水面波动大小难以精确控制，WSAW 的SNR 出现波动，但随着雷达倾斜角度的增大，WSAW 的SNR 变化并不明显。由此得出结论，雷达倾斜角度对WSAW 信号提取效果基本没有影响，推测其原因是在实验中由于雷达保持在声源的正上方，仅改变雷达的倾斜角度几乎不会影响雷达对水面回波的接收效果。

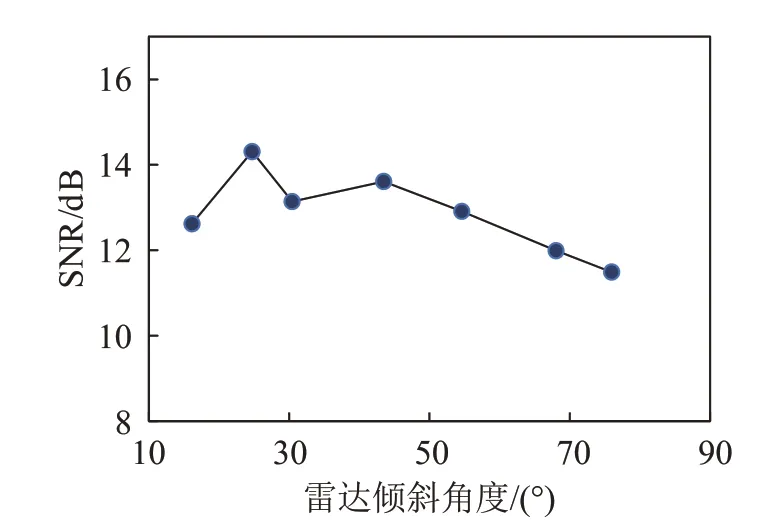
图16 不同倾斜角度下WSAW信号的SNRFig.16 SNRs of WSAW signal at different radar tilt angles

4 结 论

本文提出了一种基于级联成像FMCW 雷达的WSAW信号提取处理方法。

针对厘米级的大幅度自然扰动，本文采用了多角度积累结合阈值相位补偿的方法，从而减小RCS剧烈起伏造成的影响；水下声源采用线性调频信号并结合匹配滤波技术提高信噪比，为在更大、更复杂的水面扰动下通信提供了思路。

本文通过多次实验比较了不同扰动下的WSAW信号的提取及处理的效果。实验结果表明，随着自然扰动波高的增大，提取到WSAW 信号的SNR逐渐降低，在1.5 cm的扰动波高下依然可以有效提取WSAW 信号并进行解码；同时设计实验验证了在毫米级扰动下FMCW 雷达倾斜50°提取WSAW信号的可行性。虽然本文的实验尺度较小，但通过提高水下声源的声源级和方向性可以在保证WSAW 信号幅度不变的情况下增大声源到水面的距离。

此外，在海洋环境中通常难以达到最大1.5 cm的扰动波高，在本文的基础上后续可以考虑以下几个方面以实现更大扰动的跨介质通信：(1)改变水下声源的调制方式，比如采用抗干扰更强的编码方式；(2)改进雷达信号处理算法，采用脉冲积累、改进波束形成算法以提高对水面扰动的抗干扰能力；(3)实时统计水面各处的扰动大小并动态调整通信的水空分界位置，以保证在较小的扰动下进行通信。