融合Tent混沌和维度学习的阴阳对算法
李大海,刘庆腾,王振东
(江西理工大学 信息工程学院,江西 赣州 341000)
0 引 言
目前,越来越多的非线性、高维度的工业类优化问题已难以使用传统优化方法进行求解。随机搜索算法因为其易于实现,并且具有的灵活性、以及高效性,正被越来越广泛的应用于此类优化问题。
阴阳对算法(Yin Yang pair optimization,YYPO)是Punnathanam等[1]受中国古代阴阳平衡思想启发提出的一种轻量级单目标随机搜索算法,其基于阳点(P1)和阴点(P2)的两点的交换实现搜索。YYPO算法的优点是设置参数较少,时间复杂度相对较低,缺点是在求解复杂困难的优化问题时,易早熟收敛。
目前已有诸多YYPO的改进算法被提出。Punnathanam和Debasis等[3]提出的改进阴阳对优化算法一定程度上提高了算法的收敛性能,但同样存在对于优化复杂问题时易早熟收敛的缺陷。Song等[4]提出了一种改进阴阳对算法3D-YYPO(3 dimensional Yin Yang pair optimization)提高了算法的收敛速度。李大海等[5]提出的改进阴阳对算法YYPO-SA(Yin Yang pair optimization with simulated annealing),实验结果表明YYPO-SA在统计学意义上拥有更稳定求解的能力以及更高的计算精度,并且YYPO-SA1比YYPO-SA2具有轻微的性能优势。
本文提出了一种基于YYPO-SA1的改进阴阳对算法YYPO-TP。YYPO-TP采用了以下的2个改进措施:
(1)引入Tent混沌机制优化P1和P2两点的初始位置的分布。其目的是使生成的P1和P2两点初始分布更加均匀,以增强算法的全局搜索能力,从而提高算法的性能。
(2)引入关于P1和P2两点的基于维度学习策略的新分割方式。新分割方式舍弃了原YYPO算法中使用的单向分割与D向分割方式,引入类似于PSO算法中的全局最佳粒子和局部最佳粒子,并使用维度学习策略以等概率进行正向搜索和反向搜索进行P1和P2两点的分割更新。
为测试YYPO-TP的性能,本文选用了16个CEC2013的测试函数作为性能基准函数,并将YYPO-TP和7个经典的对比算法进行性能测试和比较。并将算法应用在风力发电机的工程优化上也取得了较优效果。
1 YYPO
阴阳对优化算法将所有的决策变量都归一化处理(介于0到1之间)。若设f(x),x=(x1,…,xn)∈Rn是待寻优的函数。当YYPO完成归一化处理后,x应满足条件:0≤xi≤1,1≤i≤n。
如前文所述,YYPO的核心思想是基于P1和P2两点的交换机制进行问题最优解的搜索,其中点P1专注于局部搜索,而点P2侧重于全局搜索。在基本YYPO中,P1和P2是以参数δ1和δ2为半径的解搜索空间中的超球体的球心。在搜索时,新的附加点始终产生在两个超球体的内部,并且周期性的减小δ1和增大δ2。YYPO存在3个用户自定义的参数 (Imin,Imax,α), 其中Imin和Imax分别为存档次数I的最大值和最小值,α是固定的缩放因子。YYPO在搜索时通过缩放因子α按以下的式(1)来控制搜索半径的缩放
{δ1=δ1-(δ1/α)
δ2=δ2+(δ2/α)
(1)
YYPO同时通过采用等概率的进行单向分割与D向分割在P1和P2为球心的超球体内部产生2D个新的附加点。其中单向分割的更新式(2)如下所示
{NPjk=Pj+r*δ,k=1,2,…D
NPjk=Pj-r*δ,k=D+1,D+2…2D
(2)
D向分割的更新式(3)如下所示
{NPjk=Pj+r*δ/2,Bjk=1NPjk=Pj-r*δ/2,Bjk=0
k=1,2,3,…2D,j=1,2,3…D
(3)
式中:下标表示点数(或行),上标表示决策变量数(或列),r是介于0到1之间的随机数。由于在NP中每个点的每个变量生成一个新的随机数r,所以需要2D*D个随机数。B是一个长度为D的二维随机二进制字符串矩阵。
2 改进阴阳对算法YYPO-TP
2.1 Tent混沌映射
YYPO是根据优化问题的维度D使用简单的伪随机数序列初始化P1和P2两点的位置。文献[6]表明搜索点的初始位置的分布对于搜索算法的性能有较大的影响。Mirjalili等[7]也在文献中指出增强初始化寻优点的遍历性,可以改善其分布均匀性,进而增强算法的全局搜索能力。
混沌是非线性确定系统中由于内在随机性而产生的一种复杂的动力学行为,具有随机性规律性和遍历性等特点[8]。例如,Shao等[6]提出一种用混沌映射改进种群初始点分布的PSO算法,实验结果表明采用混沌映射改进粒子的初始分布能够获取较大的性能改善。Dai等[9]提出一种自适应混沌模拟退火算法,其使用Tent混沌映射改进了初始分布,也提高了算法的优化性能。目前常用的混沌序列是Logistic映射和Tent映射。岳龙飞等[10]发现Tent混沌映射在遍历性,均匀性和迭代速度方面比logistic混沌映射具有更大优势。
本文选用Tent映射改进YYPO算法的P1和P2两点的初始分布。Tent映射公式如式(4)所示
Pia={2Pia-1,0≤Pia-1≤0.5
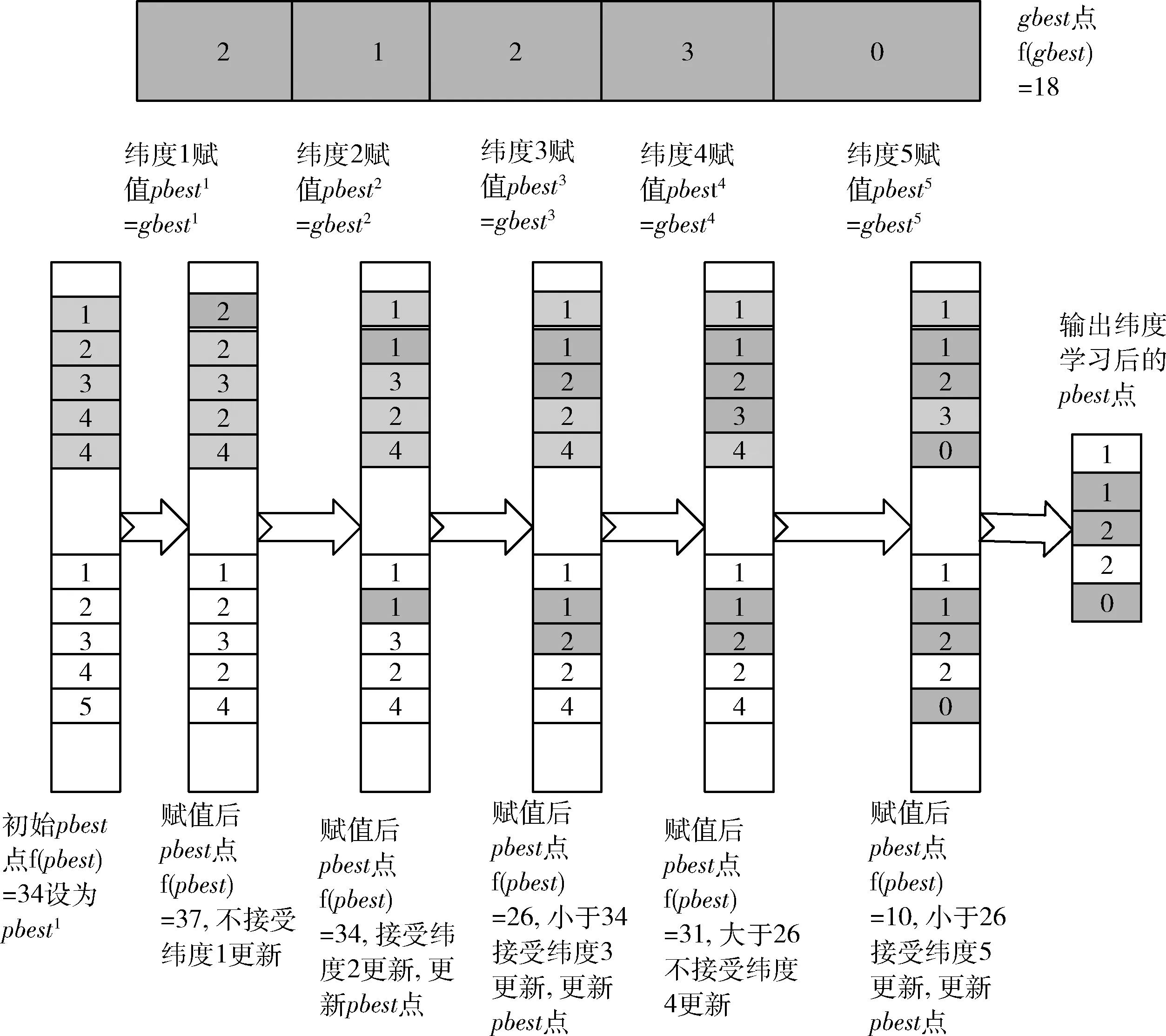
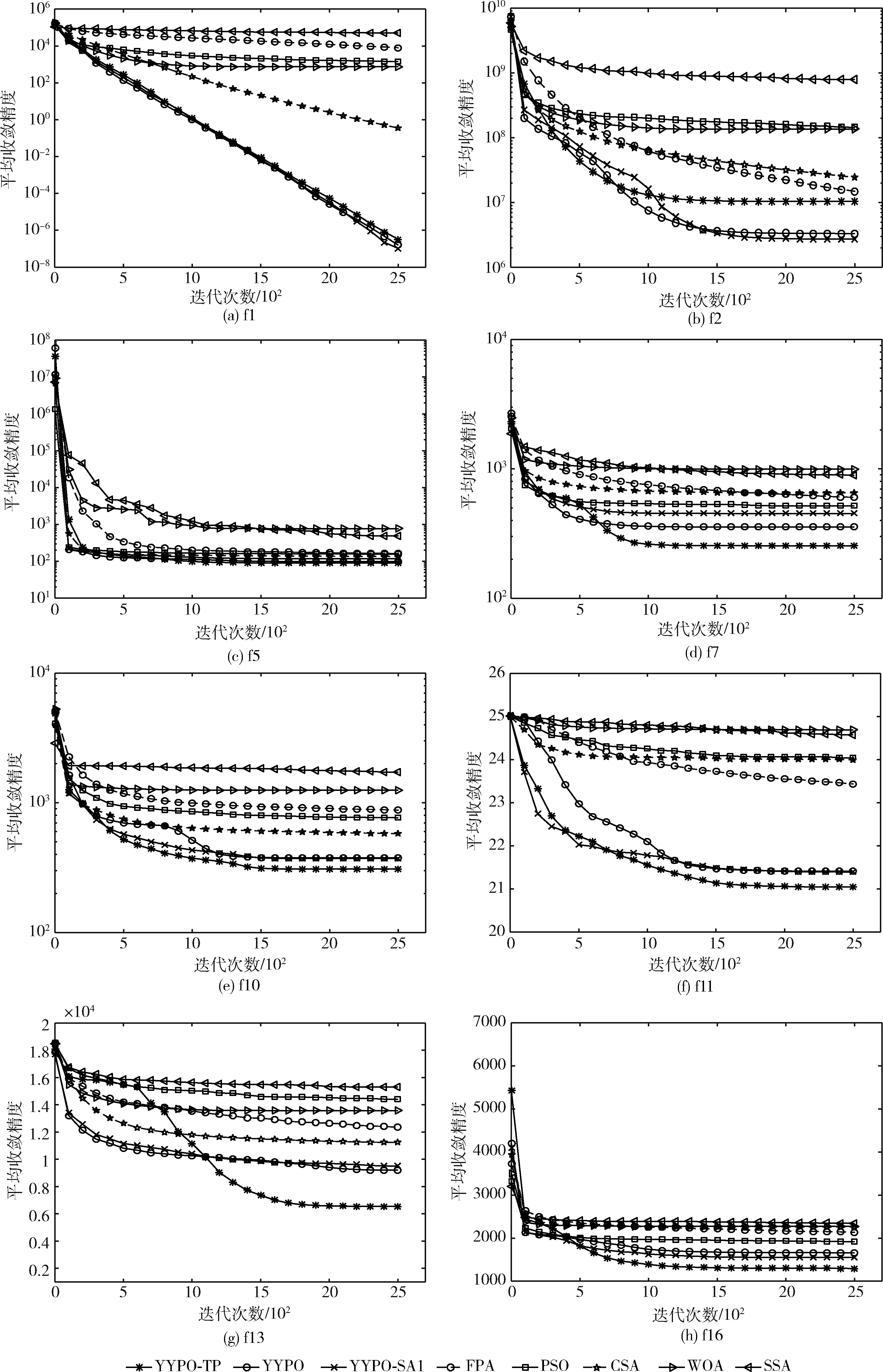
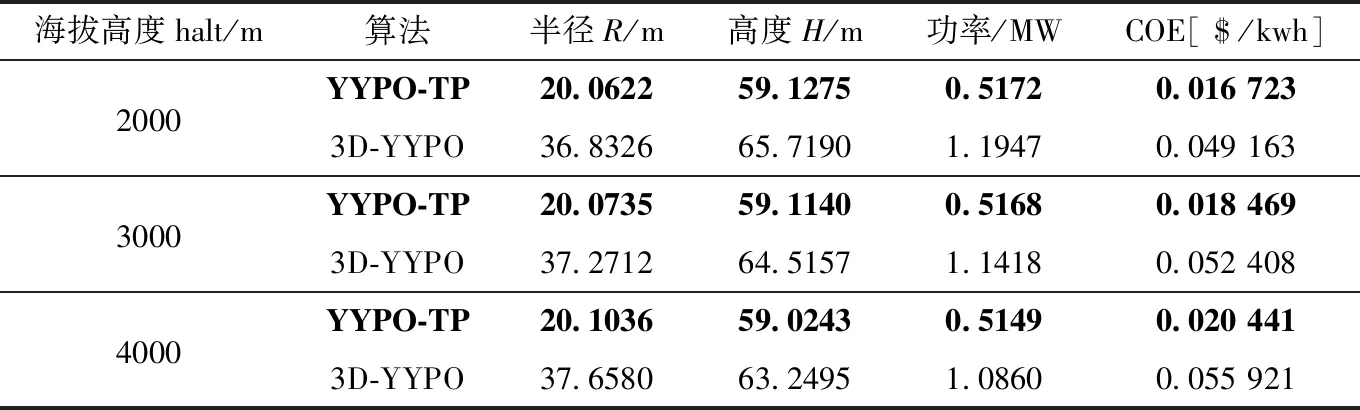
2(1-Pia-1),0.5 i=1,2,…D (4) 其中,初始点P的下标a表示混沌迭代次数,上标i表示初始点P所在的维度,D为初始点的维度,最大迭代次数设为500。Li等[11]发现,当Pia的值为0,0.25,0.5和0.75时,Tent混沌映射会陷入小周期循环,所以当Pia的值为0,0.25,0.5,0.75时,本文采用的方法是重新给Pia赋一个介于0至1的随机值。 本文使用Tent混沌映射初始化P1和P2两点的初始位置的具体步骤如下所示: (1)随机生成一个维度为D,并且各维的取值都介于0至1之间的初始点P。 (2)将P点每一维度的值Pia根据式(4)进行Tent混沌映射。生成一个新的D维的混沌点,为了避免小周期循环,当新的混沌点Pia值为0,0.25,0.5,0.75时,重新赋一个介于0至1的随机值。 (3)计算新产生的混沌点的适应度值,继续进行Tent混沌产生下一个混沌点。 (4)达到最大混沌迭代次数时终止,输出适应度值最优和次优的两点,并分别设为P1和P2的初始位置。 由式(2)和式(3)可知,YYPO使用的单向分割和D向分割本质上都不具备方向性并且YYPO的两点交换策略也只选择每次分割后得到的最优的两个点分别作为P1和P2,其没有充分利用在各维度上已经探索到的有效信息。本文提出了一种新的分割方式,受PSO全局最优点gbest和局部最优点pbest领导粒子群的寻优模式的启发,新分割方式也引入了全局最优点gbest和局部最优点pbest并以等概率进行正向或反向搜索,同时也引入了Xu等[12]提出的维度学习策略。在新分割方式中,全局最佳点gbest是在当前迭代中适应度最佳的点,初始的局部最优点pbest设为P1和P2两点位置的维度平均值,后续的pbest则在迭代中通过维度学习策略进行调整。 维度学习策略利用已知的多维信息算法性能,能够让算法获得更多有效的信息增强算法的性能[13]。例如,Xu等[12]提出了一种维度学习策略改进的PSO算法,将种群分为两个子种群并使用不同的维度学习策略让个体最佳粒子向全局最优粒子学习。Liu等[13]提出一种维度均值策略改进的PSO算法,利用粒子在多维度空间探索到的有效信息改进算法的个体最佳粒子点,平衡了算法的全局开发和局部探索。 新分割方式采用维度学习的基本思想是让个体适应度最佳点pbest向全局适应度最佳的点gbest学习。因为在多维度问题中可能不是gbest点的所有维度的值都值得学习,所以应挑选gbest点的某些维度的值进行学习。本文采用的维度学习的伪代码如下: 输入:pbest点和gbest点(假设是求优化函数f最小值) 输出:维度学习策略优化后的pbest点 (1)计算初始pbest点的适应度值f(pbest)。 (2)for i = 1 toD(其中D为优化问题的维度): (5)end for循环 (6)输出经维度学习后的pbest。 图1 维度学习过程 新分割方式使用正向搜索是为了增加搜索的方向性,因为全局适应度值最佳的粒子gbest和经过维度学习策略的粒子pbest给出了潜在的最优解所在的方向,新分割方式加入反向搜索[14]的策略是让算法在当前解的反方向进行搜索以进一步提高算法跳出局部最优的能力,因为Rahnamayan等[15]证明当前解存在50%的概率比其反向解更远离最优解。这种正反向搜索的思想也和阴阳对算法中基本的阴阳转换的思想相契合。YYPO-TP的分割方式仍保留了YYPO分割方式中将P1和P2复制2D份存储在NP中的操作,NP可视为一个2D*D维度的矩阵。其具体的分割公式如下 {NPjk=Pj+(c1*r1*(pbestj-Pj)+ c2*r2*(gbestj-Pj))*δ,r<0.5 NPjk=Pj-(c1*r1*(pbestj-Pj)+ c2*r2*(gbestj-Pj))*δ,r≥0.5 k=1,2,3,…2D,j=1,2,3…D (5) 其中,gbest是全局适应度值最佳点,pbest是经过维度学习策略后的点,δ是搜索半径,NPjk是指复制的2D个点中的第k个点的第j维,Pj是进行分割操作点的第j维,c1和c2是权重系数并都设为2,r,r1,r2是介于0至1之间均匀分布的随机数。当随机数r<0.5时,算法专注于侧重性更好的正向搜索,当随机数r≥0.5时算法在当前解的反方向进行探索更新。等概率的进行正向反向两种探索方式也象征着阴阳平衡。 YYPO-TP算法的伪代码如下: 输入:待寻优函数法f(本文求优化函数的最小值),用户自定义参数 (Imin,Imax,α)。 输出:全局最优点gbest的适应度值f(gbest)和位置 (1)初始化随机生成一个维数为D,取值范围在[0,1]之间的点P,将点P进行Tent混沌迭代200次,计算经过混沌后的所有点的适应度值。适应度最优的点设为P1,适应度次优的点设置为P2。 (3)当不满足迭代终止条件时对P1和P2两点分别按式(5)进行分割各生成2D个点。对于点的每一维都生成一个随机数r,若r<0.5,进行正向搜索分割更新,若r≥0.5,则进行反向搜索分割更新。 (5)将更新后两点存储在档案中,分割次数i=i+1,判断i是否等于存档数I,达到则选出存档中最优的两个点分别赋值给P1和P2。按照维度学习策略更新pbest。 (6)按照式(1)进行搜索半径更新,清空存档数据生成新的存档数。直到迭代终止。 和原YYPO算法相同,YYPO-TP算法迭代的时间复杂度也与求解问题的维度D直接相关。在YYPO-TP初始化阶段,其对P1和P2两点进行赋值时间复杂度为O(2D)。初始化后,进行混沌遍历的时间复杂度为O(D2),算法进入第一次存档后便进行分割阶段,分割阶段分割方式虽然改变,但依旧是复制了2D份副本进行更新,时间复杂度为O(D2)。适应度评估阶段对所有的点进行缩放,所以时间复杂度为O(2D*D)=O(D2)。 如果到达存档数I,则存档阶段时间复杂度为O(I),存档阶段内的维度学习策略的时间复杂度是O(D2)。 为了验证YYPO-TP算法的有效性,本文从于2013年IEEE进化计算大会中举行的单目标实参算法竞赛所使用的28个测试函数中选择了16个代表性的测试函数(其中4个单峰函数f1-f4,7个多峰函数f5-f11,5个复合函数f12-f16)作为实验的性能基准函数。各测试函数的参数取值范围统一设置为[-100,100]。各测试函数名称以及全局最优点见表1。 表1 测试函数 本文实验选取了YYPO-SA1、YYPO以及其它5个具有代表性的高性能单目标算法:乌鸦搜索算法(crow search algorithm,CSA)、粒子群优化算法(particle swarm optimization,PSO)、鲸鱼算法(whale optimization algorithm,WOA)、花授粉算法(flower pollination algorithm,FPA)、麻雀算法(sparrow search algorithm,SSA)与YYPO-TP进行性能比较。为了减少参数不同引起的差异,YYPO-TP和YYPO-SA1的3个用户自定义参数 (Imin,Imax,α) 的设置都参考原YYPO算法中的设置。PSO、CSA、WOA、SSA、FPA都是按照原文献中使用的参数进行设置,并且种群数目统一设置为30。 在实验中,将YYPO-TP、YYPO-SA1以及上述的6个算法分别在维度为10维、30维、50维的测试函数f1-f16独立运行50次,每一次算法的迭代次数2500次,考虑文章篇幅,仅列出算法在50维下的测试结果。取每50次运行后,各算法获得的测试函数的最优解的均值(Mean)和方差(Std)两项指标来评估各个算法的优化性能和稳定性。同时本文采用了排名(Rank)方法。排名的标准是首先比较各个算法的均值,均值越小,算法名次越好。若均值相等,再比较各自的方差,方差越小,则算法名次越好。 表2给出了各参与测试的算法对于16个测试函数在50维的测试的结果。各表中的最后3行中的Count表示排名为第一的总次数,Ave Rank表示平均排名情况,Total Rank表示基于Ave Rank排序的总排名情况,最优者用加粗表示。YYPO-TP在16个测试函数上取得10次最优,7个多峰函数6次排名第一,5个组合函数4次排名第一。其表明,随着测试函数维数的提升,YYPO-TP在多维函数上的性能上依旧优秀。同时,YYPO-TP的Ave rank值为1.69,仍排名第一。这表明YYPO-TP在高维的测试函数上能保持较为稳定的优化性能。 表2 维度为50时算法的比对结果 为了验证新算法YYPO-TP的改进是否有效,文本基于上述的实验数据,应用Friedman检验从统计学角度检验YYPO-TP算法优势的显著性。 Friedman检验的统计值Ff计算公式如式(6)所示 Ff=12nk(k+1)[∑jR2j-k(k-1)2/4] (6) Rj=(1/n)∑ni-1rji, 是所有问题中求出每个算法的平均排名,Ff的值越小,各算法之间的差异的显著性水平越高。 依据实验数据,对YYPO-TP和参与实验的其它算法分别进行Friedman检验。检验结果见表3,其中表中的P-value值即是式(6)的计算结果Ff, 表中其它的值是各算法的平均排名秩Rj。 从表3里面可以看出YYPO-TP在维度10维、30维、50维的16个测试函数上,通过Friedman检验获得的渐进显著性P-value值均远远小于0.01,并且维度越高差异性越大。这主要是由于对比算法随着维度的提升而精度下降。这个事实表明本文提出的算法YYPO-TP的寻优性能相比于参与评测的其它算法在统计学意义下有显著的优势。 表3 Friedman检验结果 为了验证YYPO-TP的收敛性能,图2分别给出了YYPO-TP、YYPO与YYPO-SA1、WOA、PSO、CSA、SSA、FPA在50维的8个测试函数上的算法随迭代次数收敛曲线。图中的横坐标表示迭代次数,纵坐标表示算法在当前迭代次数中找到的被测函数的收敛精度。 图2 收敛曲线 从单峰函数的收敛图2(a)、图2(b)中,可以看出YYPO-TP,YYPO和YYPO-SA1的收敛精度要高于其它比对算法虽然在单峰测试函数上,YYPO-TP的收敛精度不如YYPO-SA1,但二者的收敛速度都明显快于对比算法。 图2(c)、图2(d)、图2(e)、图2(f)显示的是各参评算法在4个50维的多峰测试函数上伴随迭代次数的收敛图。相比于单峰函数,多峰函数都具有较多的局部最优点。可以观察到,在多峰测试函数上,YYPO-TP在图2(c)、图2(d)、图2(e)、图2(f)这4个函数上达到最高的收敛精度且其达到最佳收敛精度明显优于YYPO-SA1和YYPO和其它4个对比算法。 图2(h)、图2(g)显示的是复合测试函数上伴随迭代次数的收敛图。复合函数存在较多的局部最优点。在50维的测试函数上,YYPO-TP无论是收敛速度和还是收敛精度都与YYPO非常接近,并且在组合函数图2(h)、图2(g)上,两者的表现都明显强于其它的对比算法。这表明YYPO-TP可以对复杂目标函数进行有效快速搜索的单目标优化算法。 根据以上分析,YYPO-TP是一种高效的单目标优化算法,并且YYPO-TP对于YYPO的改进措施是有效的。 能源需求的快速增长导致世界能源发展逐渐转向可再生能源。在各种可再生能源中,风能正迅速发展。据统计,至2018年,全球的风电总装机容量已达591 GW[16]。与传统能源技术相比,风能具有较高的发电成本。因此,有必要进一步降低风能的成本,使其更具竞争力。风力发电机的设计目标是通过优化风力发电机组参数来优化风力发电机的性能,并降低生产成本。随着海拔的升高,空气密度和气压发生变化,其对风力发电机成本和生产率的影响不容忽视。具体表现为成本增加,生产率降低,导致能源成本增加[4]。为了使经济效益最大化,可以选择不同的技术经济模型来分析风电场的投资和建设可行性。其中,COE(cost of energy)是最常用的评价指标。COE是指每生产1 KWh电能的成本,包括年能源生产成本和年能源产量。目前,风力发电机组优化设计中广泛使用的COE模型主要来自“国家可再生能源实验室风力发电机组设计成本和比例模型”的研究成果[17]。 该模型由两部分组成:年生产成本(annual production cost,APC)和年发电量(annual energy production,AEP)。COE的获得表达式可由年生产成本与年发电量的比值得到,如式(7)所示 COE=APCAEP (7) 本文使用参考文献[4]中关于高海拔风力发电机的设计参数优化模型进行实验,该模型具体的表达式如式(8)所示 COE=0.00622R3.5+0.07756R3+0.0612R2.946+0.009426R2.887+0.3508R2.6578+1.3377R2.531744.992ρπR2(∫VrVcf(v)dv+∫VfVrV3rf(v)dv)+ 0.5297R2.5025-0.00701R2.5+0.06901πR2H+5.343R1.953+23.9347R+55.7435H0.4037R0.80741744.992ρπR2(∫VrVcf(v)dv+∫VfVrV3rf(v)dv)+4.041×10-7P3r-0.002445P2r+2.096P1.249r+15.0656Pr+6.8004Pr+0.00108AEP(1-halt/15000)1744.992ρπR2(∫VrVcf(v)dv+∫VfVrV3rf(v)dv)+ 8265.6416+(0.2082P3r-0.006P2r+49.4518Pr+0.5133H1.1736R1.1736)(1+hait/15000)1744.992ρπR2(∫VrVcf(v)dv+∫VfVrV3rf(v)dv)+0.007(1+halt/15000) (8) 其中,R是风力发电机轮廓转子的半径,ρ是空气密度,H是风力发电机轮廓的高度,Vc是让风力发电机工作的最小风速,Vr是风力发电机达到额定功率发电的额定风速,Vf是风力发电机工作的最大风速,超过最大风速发电机会停止发电,Pr是风力发电机的额定功率,halt是发电机所在的海拔高度。 因为制作工艺对于轮廓转子半径R和轮廓转子高度H和额定功率Pr有着一定的约束关系,所以为了满足结构约束,轮毂高度设定为转子半径的1.5~3倍,额定功率设定为转子半径的20~40倍。为了公式化这个优化问题,适应度函数和结构约束如式(9)所示 {COEmin(R,H,Pr)=min(COE(R,H,Pr)) 1.5R Rmin≤R≤Rmax,Hmin≤H≤Hmax,Pminr≤Pr≤Pmaxr (9) 本文实验的参数设置半径R的范围为20 m~50 m,高度H的范围为10 m~150 m,功率Pr范围为100 kw~3000 kw,工作最小风速Vc和最大风速Vf分别为3 m/s和25 m/s。使用风机优化的原文献[4]中提出的3D-YYPO算法与YYPO-TP算法分别对于海拔高度为2000 m、3000 m、4000 m的3种情况来优化的风机的3个参数:轮廓转子的半径R、轮廓转子高度H、额定功率Pr以及COE。3D-YYPO的参数参考文献进行设置。YYPO-TP的参数与前述实验使用的设置相同。 不同海拔高度下两种优化算法得到的风机最优参数见表4。YYPO-TP获得的最小COE值和相应的参数要优于3D-YYPO。当高度从2000 m 增加到4000 m 时,转子半径R有着些许的减少,轮毂高度从59.1275 m变化到59.0243 m,额定功率从0.5172兆瓦变化到0.5149兆瓦,COE从0.016 723千瓦小时增加到0.020 441千瓦小时。即随着海拔高度的升高平均每千瓦时发电量的成本在增加,原因主要是海拔升高空气密度变小,以及维护的成本增加。从表4中的COE值来看,YYPO-TP要明显优于3D-YYPO。 表4 不同海拔高度下算法优化得到的最优结果 本文提出的YYPO-TP算法是在YYPO算法基础上运用Tent混沌策略增强算法P1和P2点初始位置分布的均匀性,引入基于全局和局部最优点导向的正向和反向分割机制并利用了维度学习策略,以更好利用已知探索到的有效信息增强算法的搜索能力。基于16个测试函数上的测试结果,应用Friedman检验,YYPO-TP在统计学意义上优于YYPO和YYPO-SA1,并显著优于其它参与评测的5个算法。在高海拔风力发电机的设计参数优问题上,YYPO-TP也能获得优于3D-YYPO的优化性能。 YYPO-TP算法在单峰函数上效果不理想,这可能与算法设计的分割模式有关,过强的随机性可能让算法在只有一个全局最优点的单峰测试函数无法快速获得最优解。这也是今后值得改进的一个方向。2.2 正反向搜索和维度学习策略





2.3 时间复杂度分析
3 实验结果与分析
3.1 实验设计

3.2 实验结果分析

3.3 Friedman检验

3.4 收敛情况分析
4 高海拔风力发电机
5 结束语

