多径效应下变分贝叶斯压缩感知无源定位方法

李华静，李 宁，郭 艳，盛金锋，陈 承

(中国人民解放军陆军工程大学 通信工程学院，江苏 南京 210007)

0 引 言

随着智能时代的到来，用户对位置信息的需求日益增长。目前，已有多种成熟的目标定位系统被广泛应用于国防事业、电力调度、救灾减灾、应急搜救等众多领域[1，2]，如北斗定位系统(BeiDou navigation satellite system，BDS)以及基于移动蜂窝网的定位系统。这些定位系统能够满足用户在众多应用场景下的定位需求，同时也为目标定位技术的进一步发展奠定了必要基础。当待定位目标自身无法搭载卫星无线地面接收定位装置或者在其自身希望不被卫星监测定位或追踪定位的特殊情景中，传统的卫星定位技术和卫星有源定位技术[3，4]等方法都不再适用。面对这种复杂情景，学者们给出了一种不需要依赖目标发射无线信息的无源被动定位方法[5，6](device-free localization，DFL)。

现有的无源被动定位技术利用较多的信息有两种：其一是接收信号强度[7](received signal strength，RSS)，其二是信道状态信息[8](channel state information，CSI)。然而大多无线传感器设备都不能直接利用具有细粒度的CSI，在此情况下，与CSI相比无线传感器本身具有的信息RSS则显得极易获取并且后续加工处理也相对简便。因此，基于RSS的无源被动定位技术是解决DFL问题的首选方案。

根据对无线信号处理方式的不同，现有的基于RSS的无源被动定位技术主要可分为如下4类：①基于几何法的无源被动定位技术[9]；②基于指纹法的无源被动定位技术[10]；③基于无线层析成像[11](radio to-mographic imaging，RTI)的无源被动定位技术；④基于压缩感知[12](compressive sensing，CS)的无源被动定位技术。其中几何法定位精度较低，指纹法耗时长，无线层析成像法对硬件要求高。而压缩感知技术的出现为实现多目标无源被动定位提供了新的思路。压缩感知技术通过对信号稀疏性的有效利用，能够在低维空间的非相关观测中，实现对高维信号的感知。在多目标无源被动定位中目标位置向量是稀疏的，因此通过非相关观测只需采集少量的测量信息，就能以极高的概率重构目标位置向量。

近年来，许多研究者对由信号中的室内多径反射引起的问题进行了大量的研究。大多数现有的DFL系统仅单纯聚焦于信号的RSS测量值。但即使在静态环境中，由于多径衰落和噪声的影响[13，14]，RSS的定位精度也很容易受到时间和空间变化的影响，故单纯聚焦信号的RSS测量值并不能保证定位精度。本文提出了一种基于多径反射的变分贝叶斯压缩感知无源定位方法，在压缩感知理论体系中构建虚拟节点模型，利用多径效应下虚拟传感器的接收信号强度，在不额外增加硬件资源的情况下增加通信链路，并利用改进椭圆权重模型以量化目标阴影效应，通过处理后的通信链路接收信号强度估计目标位置，有效提高了定位精度。该方法克服了传统基于接收信号强度的压缩感知定位方法对环境敏感，以及在复杂变化环境下定位精度下降的问题，并且在同等传感器数量的条件下，达到更高的定位精度；另一方面，有效节约了资源，将通信链路接收到并处理后的RSS值作为观测数据，减轻了环境噪声的影响，同时进行网格裁剪，降低了运算复杂度，减少了计算时间。

1 系统模型

1.1 基本定位场景模型

传统无源定位场景设置如图1所示。待定位的无源定位目标随机分布在矩形定位区域内，矩形定位区域的四周部署着收发定位信息的传感器节点，通过测量传感器节点收发定位信息构成的通信链路，实现对无源定位目标的定位。

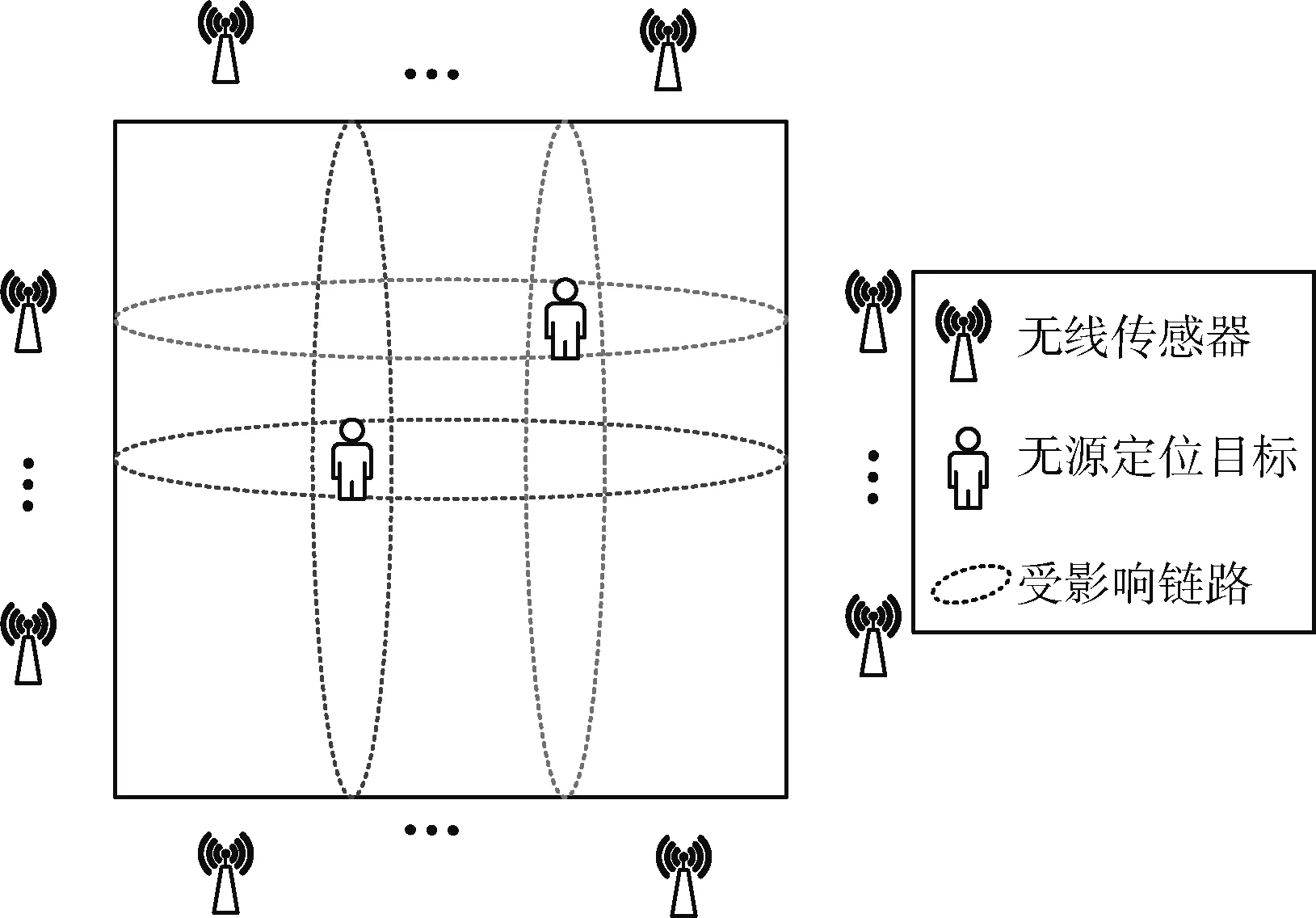
图1 传统无源定位场景

1.2 利用反射信号设计的定位场景

本文构建的无源定位场景如图2所示。为简便起见，假设定位区域仍为实线矩形区域D，待定位的无源目标随机分布在矩形定位区域内，为更好地覆盖定位区域，智能反射面分别部署在定位区域东、南、西、北的边界外，构成比定位区域更大的矩形区域S。在D与S之间的位置部署传感器节点，通过利用智能反射面，将来自各个传感器节点的反射信号汇集为虚拟传感器，虚拟传感器与真实传感器的排列方式为交替排列。

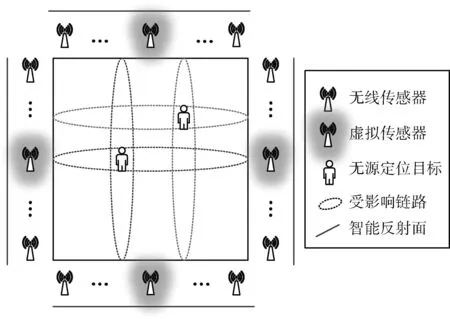
图2 无源定位场景

事实上在一般定位场景中，除了视距(line of sight，LOS)路径外，通信链路中有大量多径分量的信号传播量尚未计算出，它们以反射、衍射和折射的形式存在。而反射信号作为第二强传播信号，在以往压缩感知的建模和计算中没有考虑。因此，本文利用智能反射面反射出的定位信号，设计出虚拟传感器节点模型，如图3所示。通过虚拟传感器节点模型，将大量多径分量的反射信号建模为从反射面后的一个镜像传感器发出的信号，让实体传感器与虚拟传感器都置于智能反射面所构成的矩形内部。真实传感器与虚拟传感器交替排列的部署方式，具体可表示为

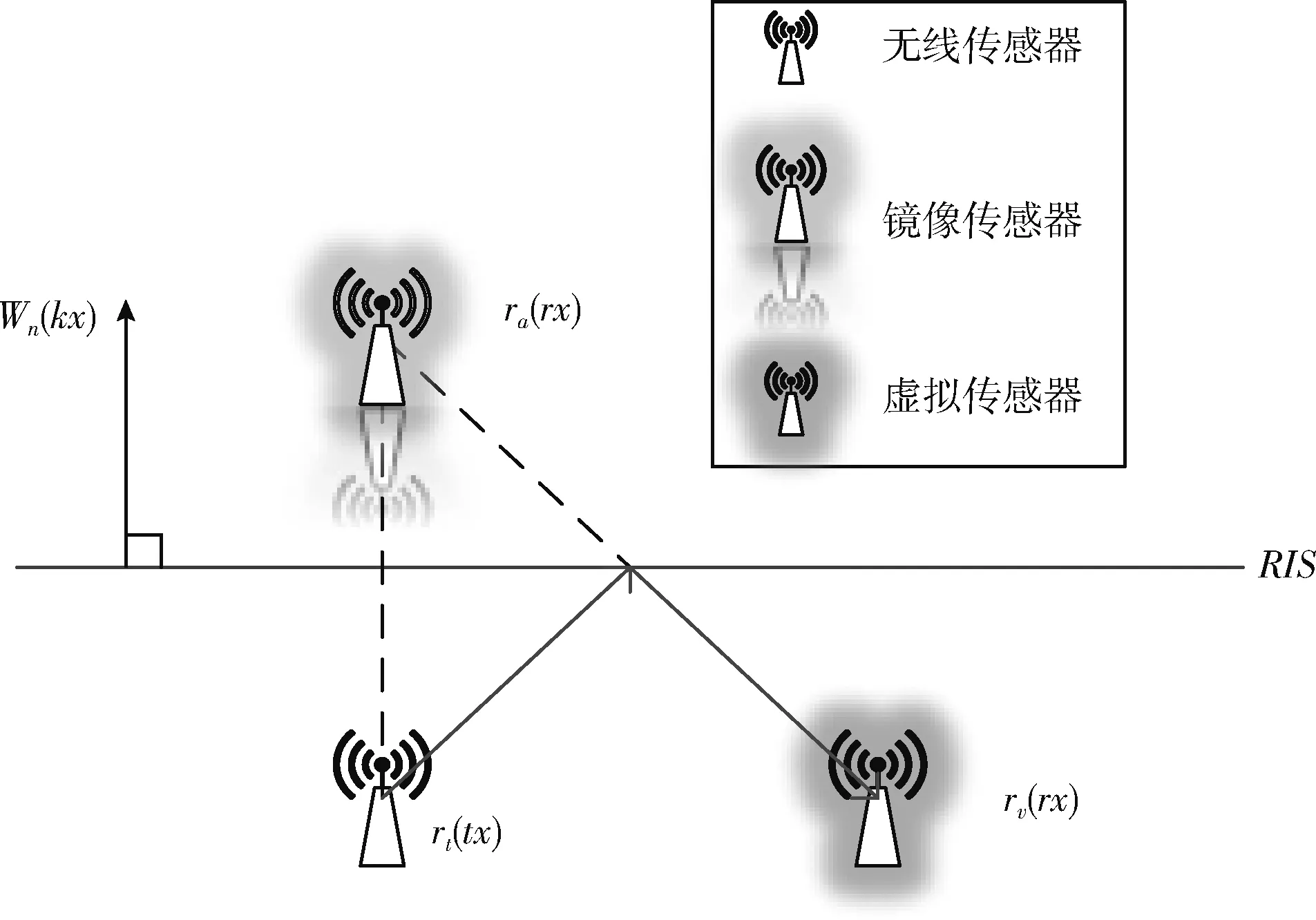
图3 虚拟传感器模型

rv(rx)=[ra(rx)-sk]Pk

(1)

其中，Pk为对称正交矩阵，可表示为Pk=E-2Wn(kx)Wn(kx)T，sk表示偏移量，可表示为sk=2rv(rx)-kx。 而Wn(kx)，k=1，2，3，4表示为反射面RIS的法向量，反射面可由齐次坐标 (Ax，Bx) 表示，则法向量可表示为

Wn(kx)=(A2x+B2x)- 12(Ax，Bx)T

(2)

根据反向光线跟踪算法[15]的解，若原始的链路总数为L，通过虚拟传感器模型，将得到L+V链路，其中V是从反向光线跟踪获得的虚拟传感器中获得的链路。由此可知，在未增加硬件耗材的情况下，使通信链路得到增加。

1.3 通信链路的空间影响区域

在设计的包含智能反射面所构成的矩形定位区域内随机分布有K个待定位目标，为估计其位置，需在包含智能反射面所构成的矩形定位区域四周部署能够采集相关RSS信息的传感器节点，并且为增加通信链路，要在两个真实传感器间部署一个虚拟传感器，具体部署结构的方式如图2所示。本文将由智能反射面反射出的信号构建为从智能反射面后的一个镜像传感器发出的信号，当若干个镜像传感器发出的信号汇集在两个真实传感器之间的位置时，就令其为虚拟传感器节点。真实传感器与虚拟传感器的接收信号强度信息均作用于通信链路中，同时利用这些定位信息计算接收信号强度的差值。为更好地覆盖定位区域，假设这些均匀部署在定位区域的边界上的真实传感器和虚拟传感器数量为2M，每两个传感器(一发一收)组成一条通信链路，则共有M条通信链路。将M条通信链路的初始接收信号强度值(不存在待定位目标即无遮挡时的信号强度值定为初始值)存储在向量中y0， 则接收信号强度的差值y可计算为

y=yk-y0

(3)

其中，yk为M条通信链路存在待定位目标(存在遮挡)时的接收信号强度值。

由于压缩感知理论针对的是离散信号，为了将压缩感知中的稀疏恢复算法用到无源定位中，需对定位区域进行网格化处理。将定位区域划分为N个大小相同的网格，并按顺序编号，即1，2，3，…，n，…，N。 用一个N维向量θN×1表示K个待定位目标 (K≪N) 的位置分布：若某个网格含有目标，则将该网格中心点在直角坐标系中的坐标位置视为目标位置，并在θN×1向量中对应位置的值置为1，其余无目标的位置则置为0。简便起见，规定每个网格内至多含有一个目标，具体的通信链路空间影响区域如图4所示。

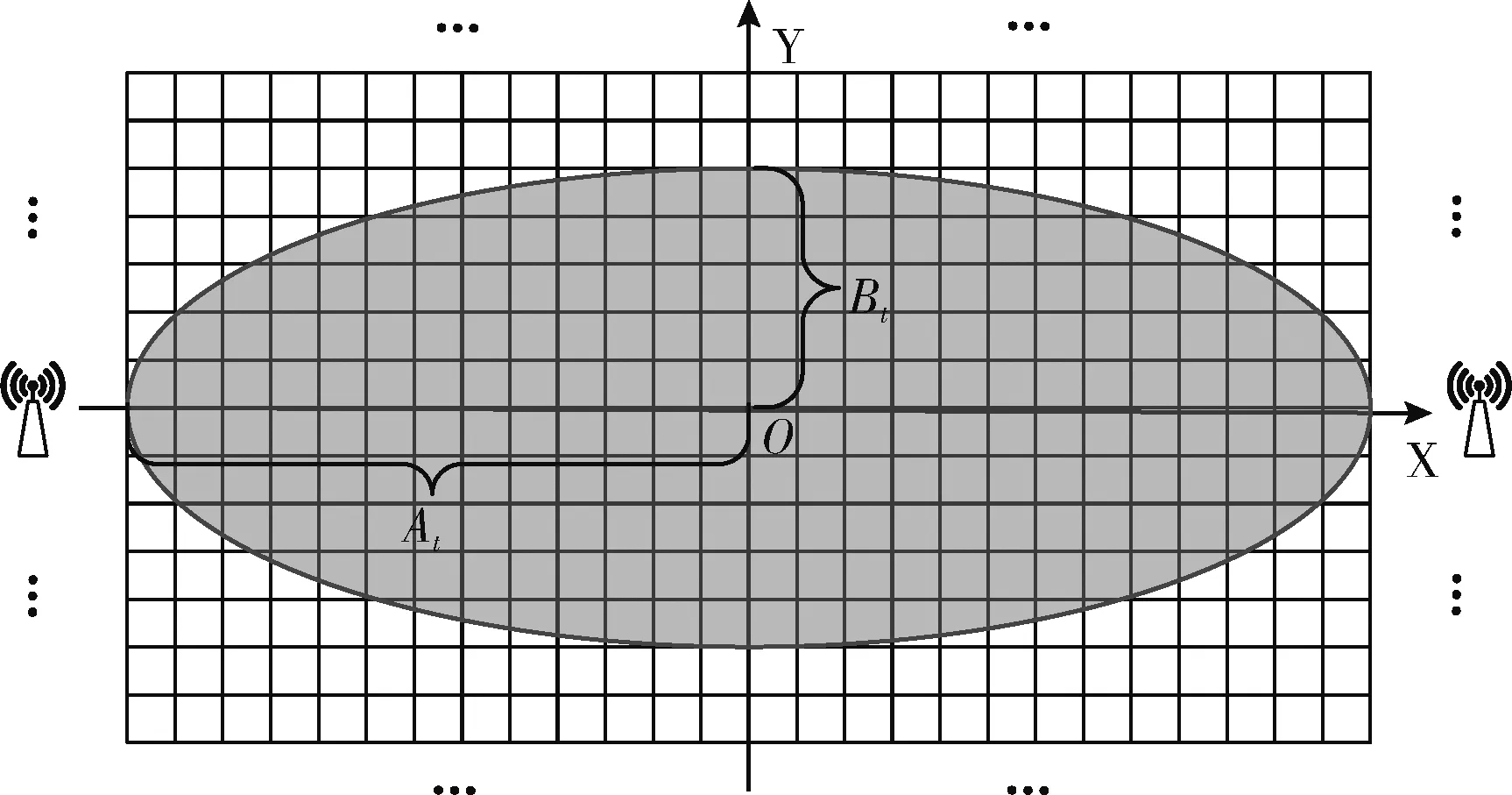
图4 通信链路空间影响区域

只有在空间影响区域内的目标才会影响该通信链路的接收信号强度信息，根据改进的椭圆权重模型，目标阴影效应所导致的信号强度的变化量可计算为

φl，i=Al·(1-cl(0.5At)2X2i+cl·(1-Y2iB2t))s.t.X2i(0.5At)2+Y2iB2t≤1

(4)

其中，φl，i表示位于第i个网格的目标对链路l的阴影效应所导致的信号偏移量，(Xi，Yi) 为第i个网格在X-Y坐标系中的坐标，Bt为链路l的长度，At为链路l第一菲涅尔带的最大半径，Al为链路l信号偏移量的最大值，cl为链路l中点的归一化信号偏移。从而可构建无源字典Φ

(5)

信号强度差值向量y可表示为

y=Φθ+ε

(6)

其中，ε为噪声向量，θ为N维向量。

2 基于RSSI的压缩感知定位算法

2.1 两层先验模型

为诱导目标位置向量θ的稀疏性，将引入了一个两层高斯先验模型。在先验模型的第一层，θ被定义为隐藏变量，服从高斯分布。在变分贝叶斯推理框架下，定义θ的高斯先验分布为

P(θ|α)=∏Nn=1N(θ|α，α-1n)=(2π)- N2|Λ|12·exp(- 12θTΛθ)

(7)

其中，αn为θn的逆方差，α=[α1，α2，…，αn，…αN]T，Λ=diag(α)。

将αn视为隐藏变量，假定α的先验分布为Gamma分布

p(α；c，d)=∏Nn=1Gamma(αn|c，dn)

(8)

其中，c和d={d1，d2，…，dn，…，dN} 是Gamma分布的确定性参数。

ε是零均值噪声向量，假设其逆方差为β， 则似然函数可表示为

p(y|θ，β)=(2πβ-1)- M2·exp(-β2y-Φθ22)

(9)

同理，将β也视为一个隐藏变量，假设其遵循一个带有确定性参数a和b的Gamma先验分布

p(β；a，b)=Gamma(β|a，b)

(10)

2.2 基于变分贝叶斯推理的稀疏重构

在分层先验模型中，y为观测数据即所求得的接收信号强度差值，z={θ，α，β} 为隐藏变量，可以利用变分贝叶斯推理得到z的后验分布。此外，Ω={a，b，c，d} 为先验模型中的确定性参数，通常被赋给非常小的值，此处为a=b=c=d=10-6， 为z提供非信息先验。z的对数后验近似为

lnq(θ)=〈lnp(y，z；Ω)〉q(α)q(β)+const

(11)

lnq(α)=〈lnp(y，z；Ω)〉q(θ)q(β)+const

(12)

lnq(β)=〈lnp(y，z；Ω)〉q(θ)q(α)+const

(13)

其中，q(θ)、q(α)、q(β) 分别为θ、α、β的后验分布，const表示常量，〈·〉 表示求期望，p(y，z；Ω) 表示隐藏变量z和观测数据y的联合分布。根据概率链式法则，p(y，z；Ω) 可分解为

p(y；z；Ω)=p(y|θ，β)p(θ|α)p(β；a，b)p(α；c，d)

(14)

根据α，β的分布，可得到θ的后验分布为

q(θ)=N(θ|μ，∑)

(15)

其中，μ为均值向量，∑为协方差矩阵

μ=〈β〉∑ΦTy

(16)

∑=(〈β〉ΦTΦ+〈Λ〉)-1

(17)

根据θ的分布，可得到α的后验分布为

q(α)=∏Nn=1Gamma(αn|，n)

(18)

=c+12

(19)

n=dn+12(μn)2+12∑n，n

(20)

根据θ的分布，可得到β的后验分布为

q(β)=Gamma(β|，b～)

(21)

=a+M2

(22)

b～=b+12(tr(Φ∑ΦT)+y-Φμ22)

(23)

更新α，β的期望值为

〈αn〉=d～n

(24)

〈β〉=b～

(25)

2.3 网格修剪机制

从2.2节的公式推导中，可知当隐藏变量的近似后验分布被更新时，α中的较多分量在收敛时均取较大的值。而随着αn逐渐增大时，θn就会逐渐减小。这种情况下，部分较小值的网格n对观测数据y的影响可以忽略不计。由此说明，可将对观测数据未造成过多影响的网格从网格集∏中移除，并在迭代过程中进行实时网格裁剪，从而减少计算量。实验中，主要根据α的当前近似后验分布来裁剪网格，设定阈值αth， 则每次迭代中，网格集∏被更新为

∏new=∏old-{n|〈αn〉>αth}

(26)

其中，∏new表示裁剪后的网格集，∏old表示当前未经裁剪的网格集。由裁剪后的网格集可知，对无源字典Φ进行符合网格裁剪机制的裁剪，能够保证本文中定位算法的计算量随着无用网格数量的减少而降低。

此外，在每一次迭代中，测量残差γ计算为

γ=y-Φμ2

(27)

设定测量残差阈值γth， 当γ<γth或迭代次数达到最大迭代次数时，停止判断。同时设定稀疏阈值μth， 滤除均值μ中较小的非零分量。取最后得到的均值向量μ作为无源目标定位结果。

3 仿真结果分析

本节中，进行了一系列仿真实验来验证所提算法的优越性能。在仿真中，目标监测区域A被设定为一个6.5 m×6.5 m的正方形区域。将其等分为N=169个边长为0.5 m的正方形网格。K=4个待定位目标随机分布在A中，M=26条由真实传感器和虚拟传感器构成的通信链路沿A的四周均匀分布。使用M条通信链路的接收信号强度值作为观测数据。为检验所提算法的可靠性和鲁棒性，在每个测量值上添加高斯白噪声。测量值的信噪比定义为：SNR=10lg(Φθ22/(Mσ2))， 其中σ2表示噪声向量ε的方差。仿真中，设定信噪比的默认值为20 dB。为验证所提的基于多径反射的变分贝叶斯压缩感知(multiple path variational bayesian compressed sense，MPCS)无源定位方法能够使得定位精度提高以及误差率下降，首先通过仿真验证本文所设计的网格裁剪机制相对于未裁剪机制的优越性；其次模拟现实变化的环境，提出环境影响因子的等级作为自变量，设计对比实验验证DFL-MPCS相比于其它3种算法：①基于正交匹配追踪(orthogonal matching pursuit，OMP)的无源目标定位方法；②基于变分期望最大化(variational expectation maximization，VEM)的无源目标定位方法；③基于基追踪(basic pursuit，BP)的无源目标定位方法能够更好地适应变化环境，鲁棒性更高；最后设计3组对比实验，将DFL-MPCS分别与DFL-OMP、DFL-VEM、DFL-BP这3种无源目标定位方法对比，验证所提方法能实现更高的定位精度。

3.1 验证网格裁剪机制的优越性

首先，本节设计相关仿真实验验证所提网格裁剪机制的有效性，同时研究裁剪不同阈值αth对所提算法定位性能的影响。图5展示了不同裁剪阈值 (αth=1，3，10，20，∞， 其中αth=∞为不进行网格裁剪)下，所提算法的平均定位误差(此处的平均定位误差是指真实目标位置和估计目标位置之间的平均欧氏距离)，图6展示了不同裁剪阈值下所提算法的平均定位时间。当αth=1时，平均定位误差最大，如图5所示。因为当αth的值越小时，越容易滤除包含了待定位目标的网格，而错误的裁剪将使得定位误差率大幅上升，故不应选择过于严苛的值。此外，当αth=10、αth=20和αth=∞时，定位误差范围均在可接受的范围，且差别不大，但αth=∞为未进行网格裁剪，故不纳入考虑范围。因此，单纯考虑平均定位误差这一指标时，αth=10以及αth=20均可作为合适的裁剪阈值纳入考虑范围，不会影响系统的定位精度。随着最大迭代次数τmax的增加，不采取网格裁剪机制将导致平均定位时间呈线性增加，而采取网格裁剪机制的方式其平均定位时间仅呈现小幅度上升，如图6所示。同时，阈值αth的值越小，平均定位时间越短。综上所述，采用网格裁剪机制并选用合适的阈值可有效降低运算复杂度，节省计算成本。基于以上仿真结果的相关分析，本文选取裁剪阈值αth=10， 既能使平均定位误差保持在可接受的范围，又能使平均定位时间在可接受的范围，故能够实现定位精度和计算成本均处于较佳的程度。

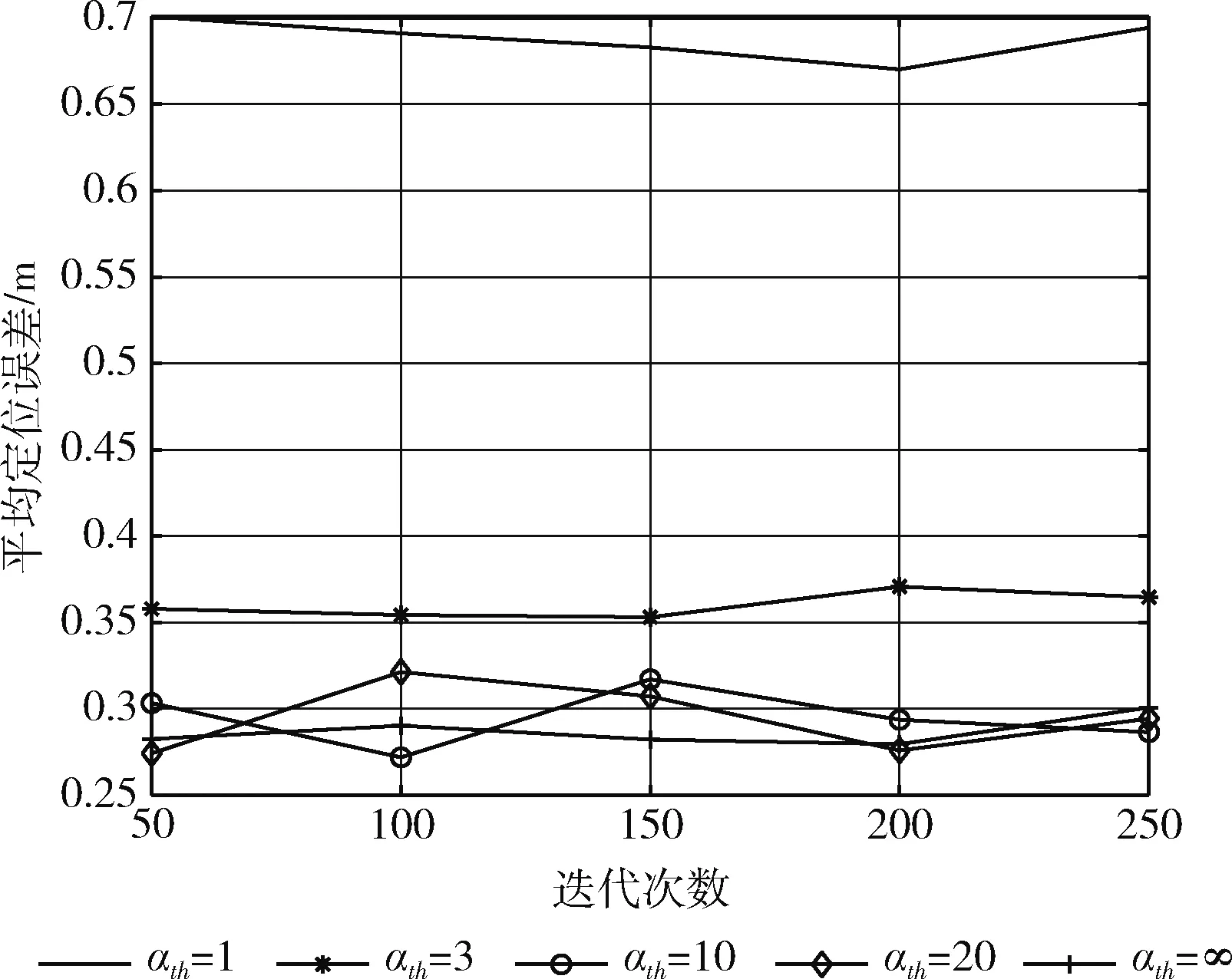
图5 平均定位误差

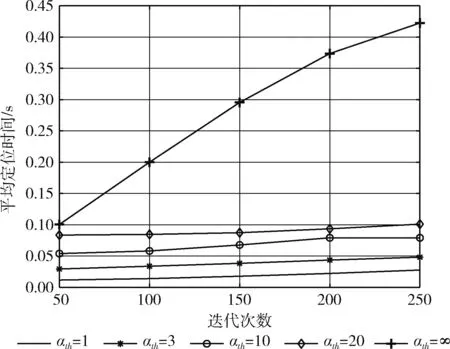
图6 平均定位时间

3.2 验证变化环境下DFL-MPCS的鲁棒性

其次，由于现实环境中影响因素不可能是单纯的理想白噪声，故本节模拟了一个变化噪声等级的环境，用于验证所提方法的鲁棒性。本文设计的变化环境中影响因子量化方法为在不断变化的环境中，将环境相关的字典参数(Ak和ck)中加入高斯白噪声。Ak和ck的值表示为

Ak(Ed)=A0+∑Edi=1εA

(28)

ck(Ed)=c0+∑Edi=1εc

(29)

其中，A0和c0分别表示为Ak和ck的初值。εA和εc均表示为加性高斯白噪声，Ak和ck的方差分别设为0.5和0.01。Ed表示为环境影响因子等级。Ak(Ed) 和ck(Ed) 表示当环境影响因子的等级为Ed时，所对应的环境相关的字典参数值。

根据以上的参数设置，构建一个环境随影响因子等级变化的无源字典Φ，并且通过Ak和ck得到不同环境影响因子等级下的模拟环境变化的测量值。如图7所示，绘制了当环境影响因子等级(Ed)由1到12时，DFL-MPCS、DFL-VEM、DFL-BP以及DFL-OMP的平均定位误差。从图中可以看出，当Ed从1升到12时，4种方法的定位误差均有相应增加。但DFL-MPCS相比于其它3种方法，其定位精度最高，由此可以表明DFL-MPCS更具有鲁棒性。

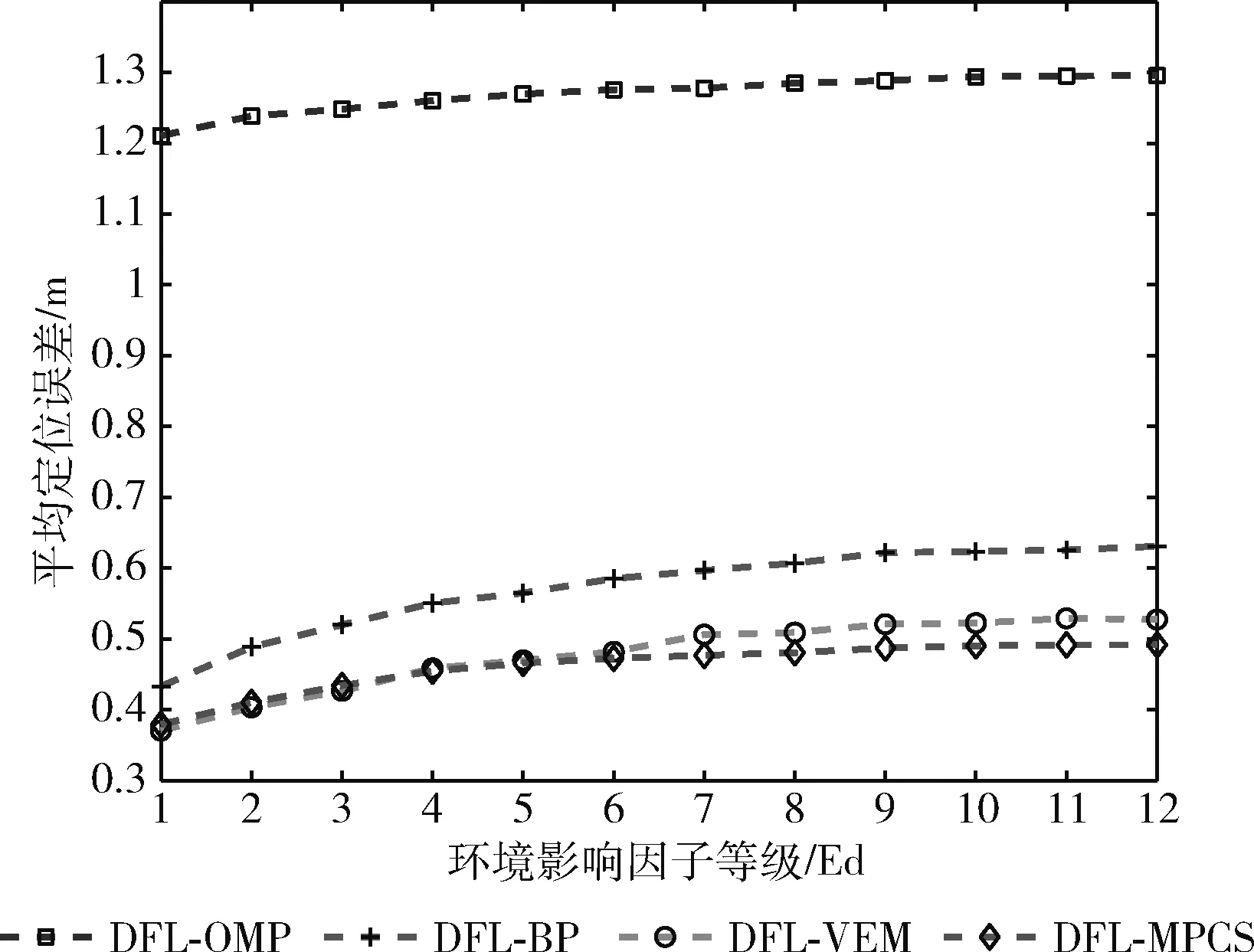
图7 变化环境中4种算法对比

3.3 验证DFL-MPCS的优越性

最后，设计3组对比实验验证DFL-MPCS与以下3种无源目标定位方法：①基于正交匹配追踪的无源目标定位方法(DFL-OMP)；②基于基于变分期望最大化的无源目标定位方法(DFL-VEM)；③基于基追踪的无源目标定位方法(DFL-BP)，相比能够实现更高的定位精度以及更低的误差率。为确保实验的严谨性以及科学性，将这3组对比实验分为两部分进行仿真实验：①验证DFL-MPCS、DFL-OMP、DFL-VEM、DFL-BP的稀疏重建性能。如图8所示，表示4个待定位目标的初始位置向量，图9则显示4种无源定位方法进行稀疏恢复后的位置向量。联立图8及图9可以看出，稀疏重构的DFL-OMP和DFL-BP的稀疏向量中有许多应当忽略但值却非零的小系数，而这些非零小系数可能会导致待定位目标计数的误差以及其定位性能的降低。稀疏重构的DFL-VEM稀疏向量中非零小系数以及显著有用系数两项指标，虽相较于DFL-OMP和DFL-BP有明显改善，但仍不如DFL-MPCS。稀疏重构的DFL-MPCS稀疏向量中非零小系数含量极少，并且显著有用系数的指标与待定位目标的初始位置向量基本保持一致。从而可以验证，DFL-MPCS的稀疏向量恢复能力优于其它3种算法。②比较通过4种无源定位方法得到的估计目标位置与真实目标位置的差距。根据图9所示的稀疏重构向量恢复图可以通过仿真得到估计目标位置。如图10所示，DFL-MPCS得到的4个待定位目标的估计位置与真实位置一致，而其它方法均存在错误的估计位置。

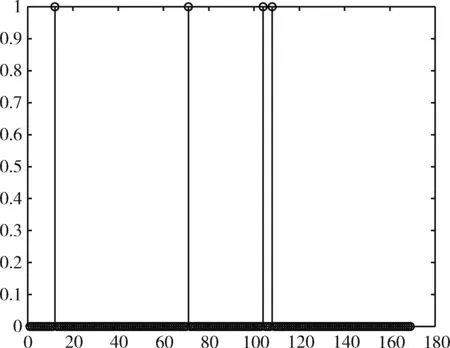
图8 原始位置向量图

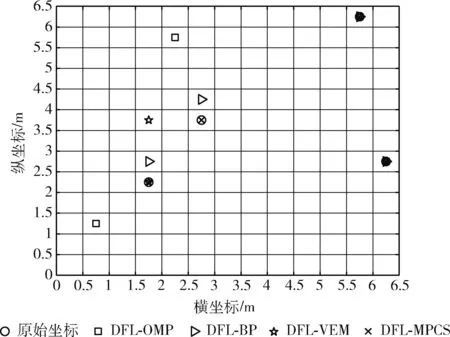
图10 4种算法估计目标与真实目标位置比较

此外，如表1所示，记录了4种无源定位方法的平均定位误差以及平均定位时间(超5500次实验)。结果清晰地表明，DFL-VEM和DFL-MPCS的平均定位误差比其余两种定位方法低，但与DFL-VEM相比，DFL-MPCS的定位时间要少近50%，说明在达到相同定位精度时，DFL-MPCS能够更快速解决问题。实际上，DFL-MPCS由于采用网格裁剪机制，从而降低了其运算复杂度，即定位时间也得到了有效的降低。

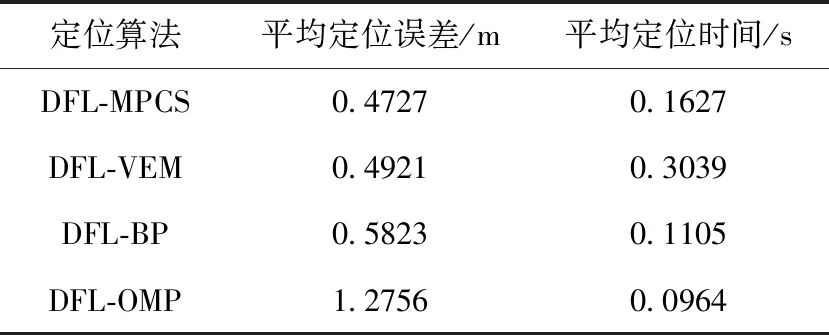
表1 不同无源定位方法性能比较

4 结束语

本文分析了多径效应下无源目标定位的特性，提出了一种利用多径效应增加通信链路提高定位性能的方法。利用智能反射面的特性构建一种基于压缩感知的系统模型，在压缩感知理论体系中构建出虚拟节点模型。在基于RSS的定位过程中，验证了应用反射信号增加通信链路的可行性。实验结果表明，DFL-MPCS方法可以有效地利用多径反射信号，以压缩感知理论以及变分贝叶斯推理稀疏恢复理论为基础，利用改进的椭圆权重模型量化目标的阴影效应，有效提高了定位精度，同时采取网格裁剪机制，降低了运算复杂度，节省了计算成本，最终达到快速精确定位。

在未来，考虑将结合智能反射面反射信号的多种特性和非基于RSS的定位方法，寻求一个更全面、更有效的无源目标定位方案，并优化解决方案，以适应更复杂的情况。