多边形的内角和与外角和的应用
郭健 刘丹丹


例题呈现
例1 如图1,一张三角形ABC纸片,点D,E分别是△ABC两边上的点.
研究(1):如果沿直线DE折叠,使点A落在CE上的点A'处,则∠BDA'与∠A的数量关系为___________.
研究(2):折成如图2所示的形状,猜想∠BDA',∠CEA'和∠A的数量关系.
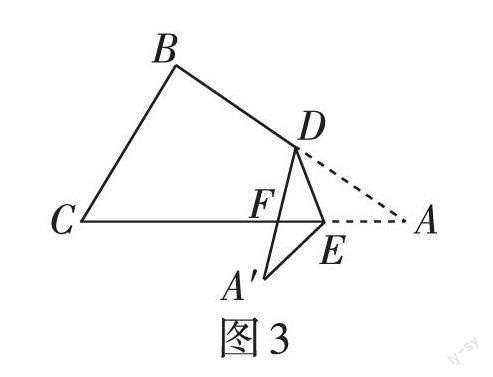
研究(3):折成如图3所示的形状,猜想∠BDA',∠CEA'和∠A的数量关系是什么,并说明理由.
解析:研究(1):解翻折问题,要从图形中找相等的量. DE为折痕,则∠A = ∠DA′A,利用三角形的外角定理可得∠BDA′ = 2∠A,故填∠BDA' = 2∠A.
研究(2):如图2,∠A与∠A′是相等的,结合四边形ADA′E的内角和为360°,∠BDA′ + ∠ADA′ = 180°,∠CEA′ + ∠A′EA = 180°,可得∠BDA′ + ∠CEA′ = 2∠A.
研究(3):如图3,由折叠可知∠A与∠A′相等,设DA′交AC于点F,运用三角形外角定理可得∠BDA′ = ∠A + ∠DFA,∠DFA = ∠A′ + ∠CEA′,可得∠BDA′ - ∠CEA′ = 2∠A.
规律:折叠中有对应角相等. 同学们在解决折叠问题时要运用一些技巧,如“将已知角放在相应三角形中”,“顺逆推、反复用”三角形内角和定理及外角定理.
例2 如图4,线段AB,CD相交于点O,连接AD,CB,我们把形如图4的图形稱为“8字形”. 如图5,在图4的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD,AB分别相交于M,N. 试解答下列问题:(1)在图4中,请直接写出∠A,∠B,∠C,∠D之间的数量关系:___________;(2)仔细观察,在图5中“8字形”的个数:___________个;(3)在图5中,当∠D = 50°,∠B = 40°时,求∠P的度数;(4)在图5中,∠D和∠B为任意角时,其他条件不变,试求∠P与∠D,∠B之间存在着怎样的数量关系. (直接写出结果,不必证明. )
解析:(1)∠A + ∠D = ∠C + ∠B. (2)6. (3)易得∠DAP + ∠D = ∠P + ∠DCP①,∠PCB + ∠B = ∠PAB + ∠P②,根据角平分线的定义,可得∠DAP = ∠PAB,∠DCP = ∠PCB,① + ②,可得2∠P = ∠D + ∠B,则∠P = 45°. (4)同(3)易得2∠P = ∠D + ∠B.
规律:遇到“两条直线相交”,常可构造或转化为“8字形”. 在图4中必有∠A + ∠D = ∠C + ∠B,在图5中必有∠P = [1/2] (∠D + ∠B).
拓展变式
例3 探究与发现:
(1)如图6①,在△ADC中,DP,CP分别平分∠ADC和∠ACD. 若∠A = 70°,则∠P =___________. 若∠A = α,用含有α的式子表示∠P为___________.
(2)如图6②,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试探究∠P与∠A + ∠B的数量关系,并说明理由.
(3)如图6③,在六边形ABCDEF中,DP,CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A + ∠B + ∠E + ∠F的数量关系:___________.
解析:(1)由∠A = 70°,可得∠ADC + ∠ACD = 110°,则∠P = 180° - (∠PDC + ∠PCD) = 180° - 1/2×110° = 125°;同理,当∠A = α时,∠P = 90° + [1/2]α. (2)由∠PDC = [1/2]∠ADC,∠PCD = [12]∠BCD,∠ADC + ∠BCD = 360° - ∠A - ∠B,易得∠P = [1/2](∠A + ∠B).(3)∠P = [1/2](∠A + ∠B + ∠E + ∠F) - 180°.
规律:求解多边形问题,可类比三角形问题的探究方法.
分层作业
难度系数:★★★★解题时间:15分钟
如图7,∠A + ∠B + ∠C + ∠D + ∠E + ∠F =___________°. 如果把图7称为二环三角形,它的内角和为∠A + ∠B + ∠C + ∠D + ∠E + ∠F;图8称为二环四边形,它的内角和为∠A + ∠B + ∠C + ∠D + ∠E + ∠F + ∠G + ∠H,则二环四边形的内角和为___________°;二环五边形的内角和为___________°;二环n边形的内角和为___________°.
〔作者单位:辽宁省实验中学(初中部)〕
答案
360 720 1080 [360(n - 2)]

