聚合酶链反应仪样本浓度示值误差校准方法

翁飞，孟盈，李腾，程时栋

（1.武汉大学中南医院设备处，武汉 430071；2.湖北省计量测试技术研究院，武汉 430223）

聚合酶链反应(PCR)[1‒2]是一种对特定的DNA或RNA 片段在体外记性快速扩增的方法，由变性、退火、延伸三个基本反应步骤构成。PCR仪是基于聚合酶链反应技术原理，模拟DNA 或RNA 的复制过程，在模板、引物、聚合酶等存在的条件下，特异扩增已知序列，对其进行检测分析的仪器设备。

根据JJF 1527—2015《聚合酶链反应分析校准规范》[3]，PCR 仪的计量特性有温度示值误差、温度均匀性、平均升温速率、平均降温速率、样本浓度示值误差、样本线性。在对样本浓度示值误差进行校准时，由于标准曲线的拟合方法、样本浓度测量平均值的计算方法存在多样性，导致样本浓度示值误差的计算以及不确定度评定方法也存在多样性。笔者通过20 组PCR 仪扩增获取的数据对这几种校准方法的结果进行对比，探讨出兼顾数据准确性和计算简洁性的PCR仪样本浓度示值误差校准方法。

1 实验部分

1.1 标准物质

该方法使用的标准物质生产机构为中国计量科学院，标准物质以重量法制备值作为标准值，并采用数字PCR方法进行突变基因拷贝数浓度验证。标准物质的相关信息如表1，其包装规格为96孔，反应孔排布图如图1，设定U1、U2为目标样本。从冰箱内取出标准物质，平衡至室温并混匀，以3 000 r/min离心后使用。

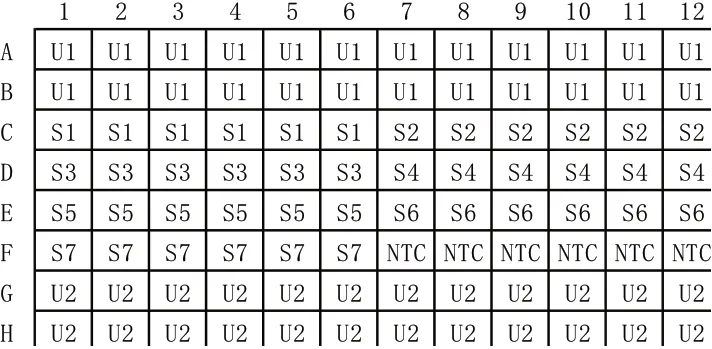
图1 PCR仪反应孔排布图

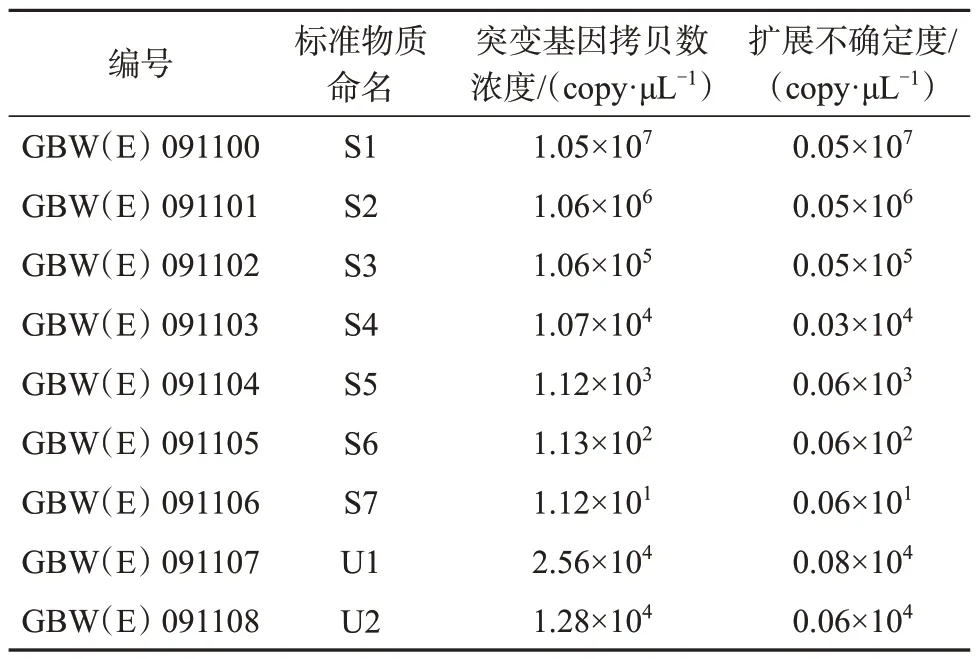
表1 标准物质的信息表

1.2 主要仪器

PCR 仪：随机选取10 台使用状况良好的96 孔的定量PCR仪作为实验用设备。

1.3 PCR仪样本浓度示值误差校准

1.3.1 校准流程

依据JJF 1527—2015《聚合酶链反应分析校准规范》，样本浓度示值误差的校准步骤如图2。

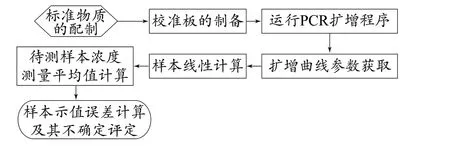
图2 PCR仪样本浓度示值误差校准步骤

PCR 仪样本浓度示值误差的不确定度评定基于GUM[4‒5]进行评定，其流程图如图3所示。

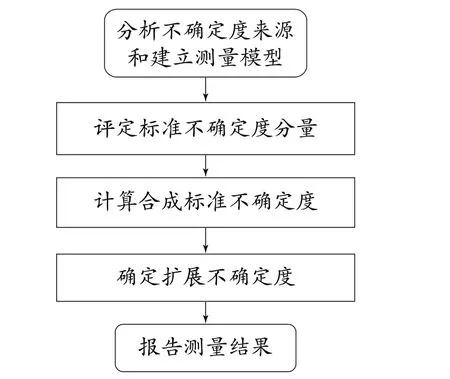
图3 基于GUM的测量不确定度评定流程图

1.3.2 校准方法

在样本浓度示值误差的校准过程中，标准曲线的拟合是基于最小二乘法[6‒7]完成，有两种方法；(1)采用配制标准物质所在反应孔的全部原始数据进行拟合；(2)先取同一浓度的标准物质所在反应孔的数据平均值，再根据这些平均值进行拟合。根据拟合的标准曲线以及样本所在反应孔扩增Ct值可求得若干个浓度对数值后，样本浓度测量平均值的计算方法有两种：(1)取浓度对数值的均值，根据均值求得对应的浓度值作为样本浓度的测量平均值；(2)求得每一个浓度对数值对应的浓度测量值，取浓度测量值的均值作为目标样本浓度的测量平均值。在标准曲线拟合和样本浓度测量平均值的计算过程中，不同方法的组合导致样本浓度示值误差的计算以及不确定度评定方法有以下4种：

方法一，标准曲线通过配制的标准物质所在反应孔的全部原始数据拟合获取，根据样本所在反应孔扩增Ct值及拟合的标准曲线求得若干个浓度对数值，取浓度对数值的均值，再根据均值求得对应的浓度值作为样本浓度的测量平均值。

方法二，标准曲线通过配制的标准物质所在反应孔的全部原始数据拟合获取，根据样本所在反应孔扩增Ct值及拟合的标准曲线求得若干个浓度对数值，求得每一个浓度对数值对应的浓度测量值，取浓度测量值的均值作为目标样本浓度的测量平均值。

方法三，标准曲线通过先取同一浓度的标准物质所在反应孔的数据平均值，再根据这些平均值进行拟合获取，根据样本所在反应孔扩增Ct值及拟合的标准曲线求得若干个浓度对数值，取浓度对数值的均值，再根据均值求得对应的浓度值作为样本浓度的测量平均值。

方法四，标准曲线通过先取同一浓度的标准物质所在反应孔的数据平均值，再根据这些平均值进行拟合获取，根据样本所在反应孔扩增Ct值及拟合的标准曲线求得若干个浓度对数值，求得每一个浓度对数值对应的浓度测量值，取浓度测量值的均值作为目标样本浓度的测量平均值。

2 PCR仪样本浓度示值误差不确定度评定

2.1 基于最小二乘法的不确定度评定

对于变量x和y，如果存在线性关系，则可以表示为y=a+bx，其中斜率b、截距a由独立测得的n组值(x1，y1)，(x2，y2)，…，(xn，yn)确定。当对测量值y进行m次测量，被测量值的估计值xˉj的不确定度计算公式为[8‒10]：

式中：xˉi——被测量值的平均值；

i——测量次数，i=1，2，…，n；

s(xˉi)——被测量值平均值的实验标准偏差；

xˉj——被测量值的估计值；

s(y)——测量值的实验标准偏差；

b——拟合线性方程的斜率；

j——测量次数，j=1，2，…，m；

xi——第i次测量值。

2.2 PCR仪样本浓度示值误差不确定度评定

2.2.1 数学模型

样本浓度示值误差测量模型为：

式中：Δc——样本浓度示值误差；

cˉ——样本浓度测量平均值；

cs——样本浓度标称值。

根据不确定度传播规律[11‒12]可知Δc不确定度的计算公式为：

其中u(cs)可以由标准物质原始浓度及稀释系数求得，因此Δc不确定度评定的关键为样本浓度测量平均值cˉ的不确定度u(cˉ)的评定。

2.2.2cˉ测量不确定度分量评定

(1)方法一。样本浓度测量平均值cˉ测量模型为：

式中：xˉ——样本浓度对数值xi的均值，i=1，2，…，n；

n——标准物质(S1～S7)反应孔的数量。

样本浓度测量平均值cˉ的不确定度为：

cˉ测量不确定度来源包括两部分：测量重复性引入的u1(xˉ)和测量模型引入的u2(xˉ)。因此样本浓度测量平均值的不确定度为：

式中：yi——标准物质所在反应孔扩增Ct值，i=1，2，…，n；

s(y)——yi的标准偏差；

k——包含因子，k=2；

ci——标准物质所在反应孔的样本浓度，i=1，2，…，n。

将公式(7)、(8)代入到公式(6)中即可得到样本浓度测量平均值cˉ的合成不确定度。

(2)方法二。目标样本浓度测量平均值测量模型为：

式中：cj——样本浓度的测量值，j=1，2，…，m。

cˉ测量不确定度来源包括两部分：测量重复性引入的u1(cˉ)；测量模型引入的u2(cˉ)。因此目标样本浓度测量平均值的不确定度：

将式(13)～(16)代入式(12)即可得到样本浓度测量平均值cˉ的合成不确定度。

(3)方法三。该方法与方法一中样本浓度测量平均值的不确定计算公式类似，同样由公式(7)、(8)代入到公式(6)，只是标准偏差s(y)计算不同：

式中：p——配制的标准物质的浓度梯度数，且由p替代公式(8)中的n。

(4)方法四。与方法二中样本浓度测量平均值的不确定计算公式类似，同样是由式(13)～(16)代入式(12)，只是用配制的标准物质的浓度梯度数p代替测量次数n。

2.2.3 Δc不确定度评定

根据公式(3)计算出u(Δc)后，样本浓度示值误差的扩展不确定度为：

3 结果分析

3.1 实验结果

运行PCR 仪扩增程序，分别用4 种方法对样本示值误差进行校准，总共进行了20组实验，4种方法的校准结果如表2所示。

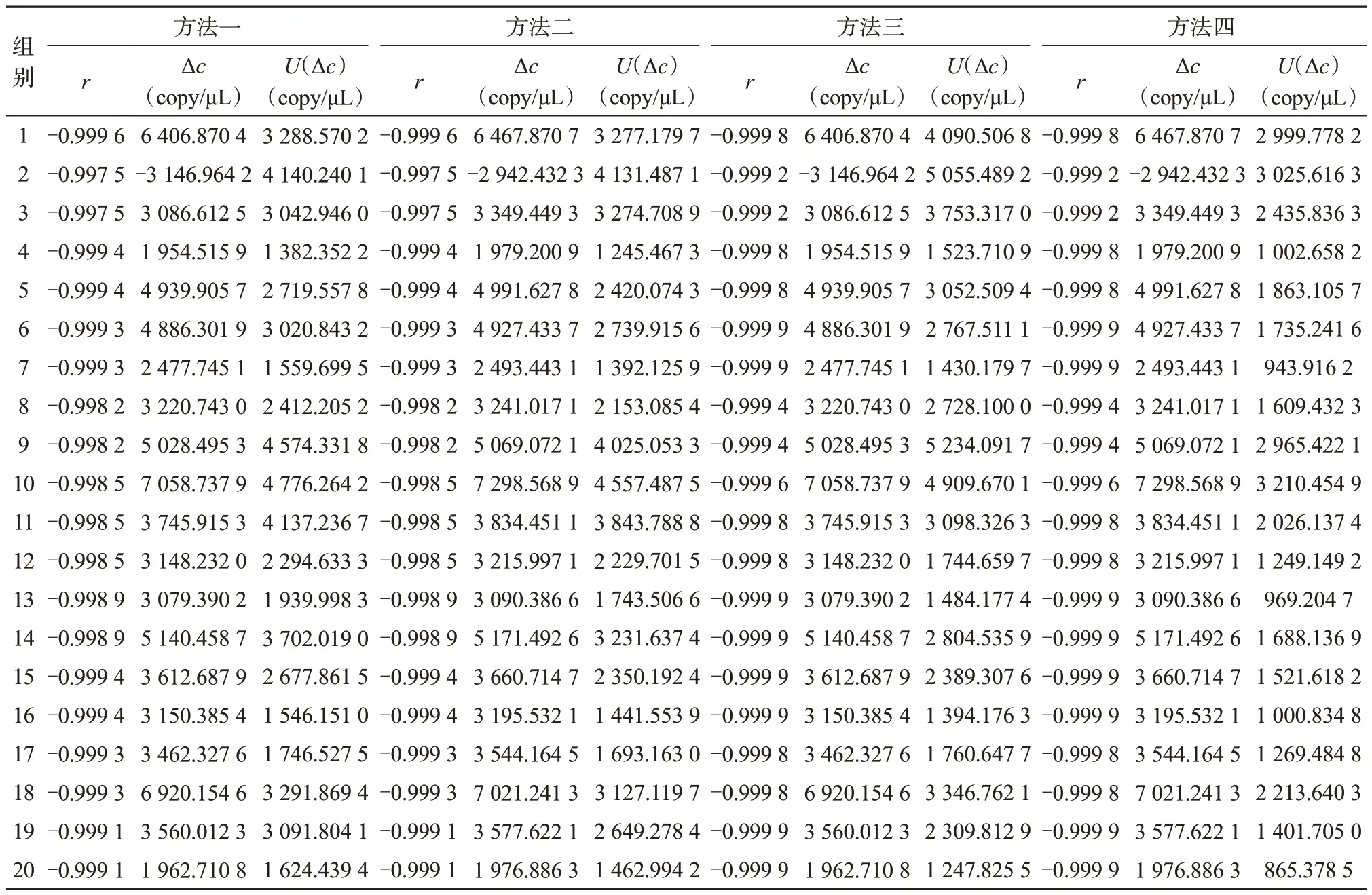
表2 4种方法的校准结果

3.2 差异显著性检验

3.2.1 样本浓度相对示值误差差异显著性检验

样本浓度相对示值误差计算公式为：δ(Δc)=Δc/cs×100%，用F检验对4 种方法计算出的样本浓度相对示值误差进行差异显著性分析[13‒15]，P=0.998>0.05，结果如表3所示。

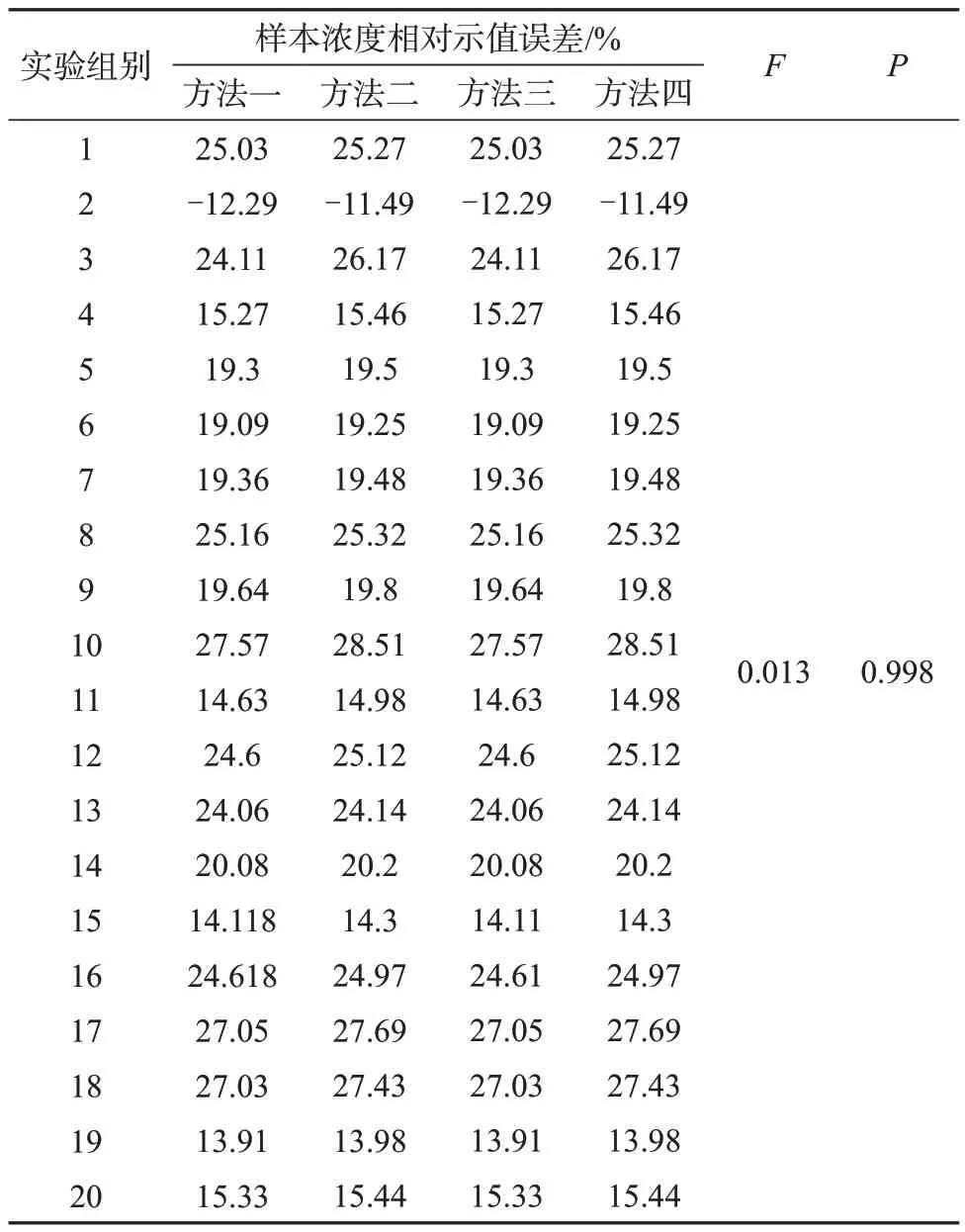
表3 样本浓度相对示值误差差异显著性检验结果

3.2.2 样本浓度示值误差相对扩展不确定度差异显著性检验

样本浓度示值误差的相对扩展不确定度[16]计算公式为：urel(Δc)=u(Δc)/Δc，用F检验对4种方法计算出的样本浓度示值误差相对扩展不确定度进行差异显著性分析，P=0.351>0.05，结果如表4。

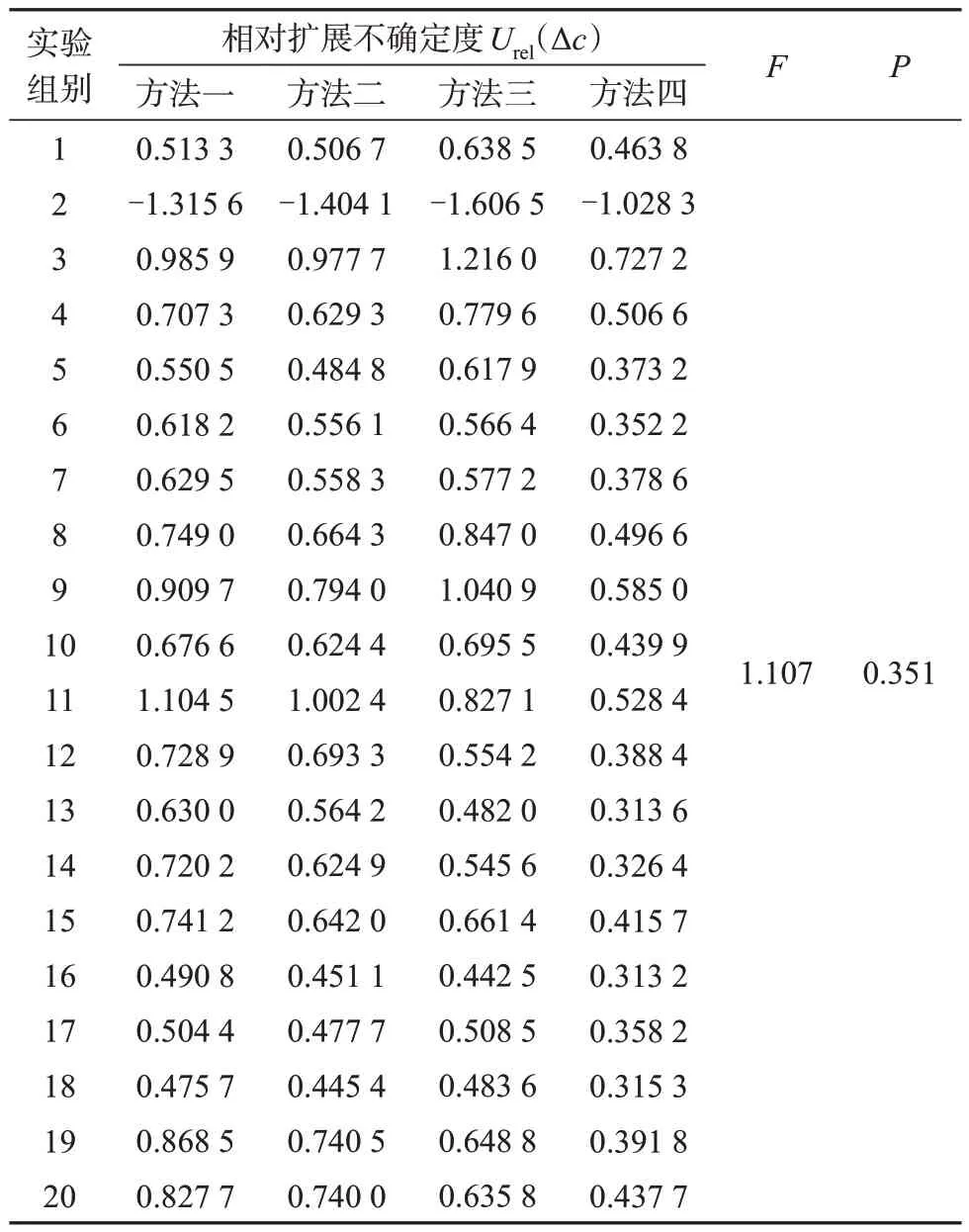
表4 样本浓度示值误差相对扩展不确定度差异显著性检验结果

3.3 结果分析

从4 种方法的计算公式可以看出：(1) 4 种方法中，方法一和方法二是基于实验原始数据进行计算，其结果更能真实反映仪器的性能；(2)方法二和方法四中的计算更为繁琐。

从表2 中的计算结果可知：(1)每一组实验结果中，方法一和方法二的相关系数r值一致，方法三和方法四的相关系数r值一致，并且后者的r值更接近1，即先将同一浓度的标准物质所在反应孔的数据取平均值，再根据这些平均值拟合标准曲线，样本线性[17]更好；(2)方法一和方法三计算得到的示值误差一样，方法二和方法四得到的示值误差一样，即样本浓度示值误差值大小只与样本浓度平均值的计算方法有关，并且方法一和方法三得到的示值误差更小；(3) 20 组实验结果中，4 种方法计算的样本浓度示值误差不确定度大小均不一致，即浓度示值误差不确定度大小与标准曲线拟合方法、样本浓度平均值的计算方法均有关，并且4 种方法中方法四计算出的不确定度值最小。

从表3中结果可知，4种方法计算的样本浓度相对示值误差差异性不显著，从表4 中的结果可知，4种方法计算的样本浓度示值误差相对不确定度差异性不显著(P=0.351>0.05)。

4 结语

基于以上的实验结果，4 种PCR 仪样本浓度示值误差校准方法的结果差异性不显著。因此综合考虑计算的复杂度、计算结果反应仪器性能的真实程度等因素，推荐采用原始数据进行标准曲线拟合、将依据浓度对数值的均值求得的浓度值作为样本浓度的测量平均值这种方法进行PCR 仪样本示值误差校准。