基于近似模型辅助智能算法的变截面点阵结构优化设计方法

向 艳, 蒋国璋,3, 张 严,3, 徐曼曼,3

(1. 武汉科技大学 冶金装备及其控制教育部重点实验室,武汉 430081;2. 武汉科技大学 机械传动与制造工程湖北省重点实验室,武汉 430081;3. 武汉科技大学 精密制造研究院,武汉 430081)

桁架类点阵结构是一种由规则点阵单胞在空间阵列组合形成的周期性结构,具有质量轻、比强度/比刚度高、减振吸能性好,且拓扑构型简单、增材成型可靠性高等优点,被广泛应用于航天器各关键承载部件设计[1-4]。作为最具应用前景的新一代轻质强韧结构,点阵结构为实现超轻质多功能一体化设计提供了新途径,通过对点阵单胞进行优化设计可以获得具有优异宏观性能的点阵结构。

现有点阵构型优化设计大多基于等截面形状的设计约束展开。近年来,随着增材制造技术的迅猛发展,变截面点阵的制造成为可能。相比等截面点阵,变截面点阵具有可拓设计空间,其力学性能也更具优势。冀宾等[5]基于解析计算和数值模拟发现3D Kagome点阵通过变截面设计,其压缩强度提高了30%。朱凌雪等[6]的研究也表明芯体截面梯度变化的点阵夹层结构吸能效率要明显优于传统等截面点阵夹层结构。Cao等[7]通过有限元模拟和准静态压缩试验发现十二面体点阵通过变截面设计,其抗压强度和屈服强度分别提高了79%和55%。雷鹏福等[8]提出了一种点阵结构节点强化技术,通过在点阵结构节点处实现自然圆角过渡的方法,改善其力学性能。Ren等[9]为了减小点阵结构的应力集中并进一步提高其刚度性能,设计了一种节点球形增强的体心立方点阵。汪飞雪等[10]考虑变截面梁和连接球体的几何构型,实现球型增强变截面四棱锥点阵结构的几何拓扑分析,并进行了基于SLM工艺的变截面四棱锥点阵结构的形变特性和力学性能分析,结果表明较传统等截面体心立方点阵结构有显著提升。上述研究工作通过对变截面点阵单胞进行优化设计,获得了点阵结构性能的进一步提升,对点阵单胞构型的优化设计具有积极的指导意义。但现有点阵构型的优化设计大多缺乏变截面点阵构型的参数化描述模型及其普适性的力学分析方法,导致点阵构型的优化难以有效开展。

现有点阵的几何模型主要采用CAD软件建模和几何隐式模型表达等方式,难以实现点阵截面形状的参数化描述,同时其等效力学性能分析方法与其几何模型描述方式密切相关,主要有解析法、试验法以及代表体元法等[11-15]。例如,基于解析法的点阵等效力学性能分析,需根据点阵的不同构型形式选择不同的解析分析方法,且对于复杂的点阵构型,推导过程繁琐复杂,难以与后续的点阵构型优化实现有效衔接。

针对点阵形状的参数化描述问题,本文采用基于水平集的显式拓扑描述函数构建变截面点阵的显式几何描述模型,实现变截面点阵几何形状的自由描述,为后续的点阵构型优化提供充分寻优空间。针对点阵的等效力学性能计算复杂,基于变截面点阵的显式拓扑描述函数,采用能量均匀化构建具有普适性的变截面点阵等效力学性能表征模型。随后,建立截面点阵几何描述参数的优化数学模型,并采用基于近似模型辅助的粒子群优化算法进行高效求解。最后,结合数值算例验证本文所提方法对变截面点阵设计的有效性,通过与等截面点阵进行对比,以显示变截面点阵设计的性能优势。

1 变截面点阵的显式几何描述

水平集方法是一种结构几何边界的隐式描述方法,其核心思想是将研究的曲线或曲面表示为高一维水平集函数的零等值线或面[16]。与传统水平集方法以自由函数或径向基函数隐式表达结构几何边界的方式不同,本文通过定义水平集函数的显式数学关系,建立结构几何的显式拓扑描述函数,实现结构几何边界的显式描述,达到通过调控水平集函数参数以精确控制结构几何的目的。以如图1(a)所示的变截面点阵杆件为例,采用如式(1)所示的基于水平集的显式拓扑描述函数实现单根变截面杆件的显式几何描述(如图1(b)所示),其中方程t(x)是点阵杆件的截面形状控制方程,通过调控截面形状控制参数t1,t2,t3可实现杆件截面形状的精确控制,图1(c)是由变截面杆件组成的体心立方点阵构型。特别地,当各杆件的截面形状控制方程参数t1,t2,t3均相等时,可获得等截面点阵构型。

图1 变截面点阵单胞示意图Fig.1 Schematic diagram of variable cross-section lattice unit cell

基于水平集函数的变截面点阵显式几何描述模型可表达为

(1)

其中,

φi(x)=max[φi,cylinder(x,y,z),φi,sphere1(x,y,z),φi,sphere2(x,y,z)]

φi,cylinder(x,y,z)=[t(x)/2]2-(sinθi·Ld)2,

φi,sphere1(x,y,z)=(t1/2)2-(x-x1)2+(y-y1)2+(z-z1)2,

φi,sphere2(x,y,z)=(t2/2)2-(x-x2)2+(y-y2)2+(z-z2)2

式中:D为整个设计域;Ω为实体材料区域;∂Ω为结构的边界;杆件部分由一个变截面柱体和两个球体组成,其水平及函数分别为φi,cylinder(x,y,z),φi,sphere1(x,y,z),φi,sphere2(x,y,z);变截面柱体的两端分别以(x1,y1,z1)和(x2,y2,z2)为中心,这两点也是两个球体的球心;(x0,y0,z0)和L分别为杆件的中心点坐标和杆件长度;t(x)为杆件的截面形状控制方程;t1,t2,t3为截面形状控制方程参数。

2 变截面点阵的等效弹性张量计算

(2)

传统均匀化方法的理论推导复杂,计算效率较低。为进一步简化点阵单胞等效力学属性的实施过程,提高其计算效率,基于单元应变能等效,式(2)可转化成另一种新形式

(3)

3 变截面点阵的优化数学模型

为实现变截面点阵的几何形状参数优化,以变截面点阵的几何描述参数为设计变量,材料用量为约束条件,最大体积模量或最大剪切模量为目标函数,建立优化数学模型

(4)

(5)

当以变截面点阵的体积模量最大为优化目标时,目标函数可定义为

(6)

4 基于近似模型辅助粒子群优化算法的求解策略

由于变截面点阵优化的设计变量较多,变量维数较高,为提升高维设计问题的优化效率[20-21],本文采用基于径向基函数(radial basis function,RBF)的近似模型辅助粒子群优化算法,以实现变截面点阵优化模型的高效求解。

4.1 RBF近似模型

RBF模型在高维建模中具有更高的建模精度和更快的建模速度,因此在近似模型辅助的粒子群优化(efficient surrogate-assisted particle swarm optimization,ESPSO)算法中,引入RBF近似模型用于粒子群优化算法中的全局和局部近似模型建模,本文使用的RBF模型定义如下:假定有n个样本点x1,x2,…,xn∈RD,对应的响应分别为f(x1),f(x2),…,f(xn),则由这n个样本点建立的RBF近似模型可以表示为

(7)

4.2 近似模型辅助的粒子群算法

作为粒子群优化算法(particle swarm optimization,PSO)的关键组成部分,粒子速度的更新方法对PSO算法的优化效率有很大影响。为了进一步提升近似模型辅助PSO算法的优化效率,ESPSO算法使用了一种新的策略更新粒子的速度,其更新方式如下

(8)

其中,

(9)

(10)

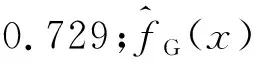
相对于传统的PSO方法,ESPSO方法改变了粒子的搜索方向。如图2所示,在PSO中,粒子朝着当前全局最优位置和当前粒子的历史最优位置即线0和1的方向搜索。而在ESPSO中,它通过由全局和局部近似模型获得的全局最优和局部最优位置即线0*和1*方向搜索,同时添加了全局和局部近似模型的最优点信息,平衡了模型的预测能力和PSO算法的全局搜索能力使其更高效。

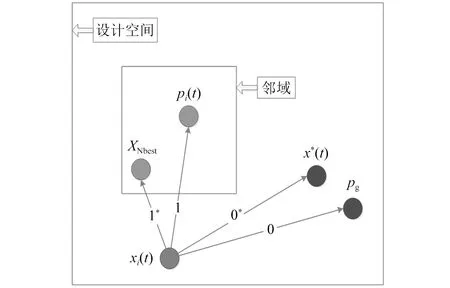
图2 ESPSO算法的搜索原理示意图Fig.2 Schematic diagram of search principle of ESPSO algorithm

在ESPSO算法中,个体历史最优粒子pi(t),i=1,2,…,N的邻域空间划分是一个重要的策略。这种空间划分策略使得ESPSO利用在邻域内获得的局部近似模型最优点来引导PSO加速搜索。此外,这种空间划分策略还考虑到了个体历史最优粒子pi(t),i=1,2,…,N的多样性,从而保证了ESPSO的全局优化效率。在ESPSO方法中,确定合适的粒子xi(t)邻域大小是非常重要的,领域空间过大粒子群会很快集中,使得ESPSO算法会陷入局部搜索。然而如果该区域太小的话模型的预测能力没能得到最大的发挥,使得ESPSO算法收敛缓慢。

因此,由Kitayama等[22]提出的计算径向基函数半径的方法被用于确定个体历史最优粒子的邻域大小。粒子pi(t)的邻域半径ri可以表示为

(11)

5 数值算例

为充分说明本文方法的有效性,分别选取BCC,FCC,BCC+FCC三种点阵构型作为代表性研究对象,采用前述构建的优化模型和ESPSO算法求解策略,实现最大体积模量或最大剪切模量的变截面点阵优化设计。同时,将变截面点阵设计结果与相应构型的等截面点阵进行对比,以验证本文方法在点阵力学性能设计上的优势。为不失一般性,在所有算例中均采用无量纲化处理,弹性模量E=1,泊松比μ=0.3,采用20×20×20=8 000个八节点六面体单元对点阵单胞设计域进行有限元离散。在每个算例中,ESPSO算法的种群大小设为N=30,在建立ESPSO的局部近似模型时,BCC,FCC,BCC+FCC三种变截面点阵构型的局部近似模型的样本点数目分别设置为大于60,180,240。

5.1 体积模量最大化的变截面点阵优化

如表1所示,是材料用量约束分别为0.1和0.3时,体积模量最大化的变截面点阵优化设计结果,包括优化后的变截面点阵构型、等效弹性张量、体积模量以及与相应几何构型的等截面点阵相比的性能提升率。从表1中的优化结果可知,在材料用量约束为0.1或0.3时,优化后的变截面点阵单胞的体积模量较相同几何构型的等截面点阵均有显著提升。如表2所示,是材料用量约束为0.3时,FCC点阵优化后的各杆件几何形状参数的最优值。虽然优化后的各杆径形状控制参数(t1,t2,t3)相差不大,但其对应变截面点阵的体积模量较相同几何构型的等截面点阵提升了7.30%。如图3所示,是其目标函数的迭代收敛曲线,整个优化迭代过程收敛平稳,目标函数最终收敛于0.665 62。

表1 体积模量最大化的变截面点阵优化结果Tab.1 Optimization results of variable cross-section lattice for maximizing bulk modulus

表2 变截面FCC点阵杆件截面几何形状参数最优值(f=0.3)Tab.2 Optimum values of cross-section geometric parameters of FCC lattice bar with variable cross-section (f=0.3)

图3 材料用量约束为0.3时,变截面FCC点阵的目标函数收敛曲线Fig.3 Convergence curve of objective function of FCC lattice with variable cross-section when the material dosage constraint is 0.3

5.2 剪切模量最大化的变截面点阵优化

如表3所示,是材料用量约束分别为0.1和0.3时,剪切模量最大化的变截面点阵优化设计结果,包括优化后的变截面点阵构型、等效弹性张量、剪切模量以及与相应几何构型的等截面点阵相比的性能提升率。其中,材料用量约束为0.1时,变截面FCC点阵优化后的各杆件截面几何形状参数的最优值如表4所示,图4是目标函数的迭代收敛曲线。根据表3的优化结果可知,当以最大化剪切模量为优化目标时,在不同材料用量约束下,优化后的变截面点阵的剪切模量均优于相应几何构型的等截面点阵。其中,当材料用量约束为0.1时,优化后的变截面FCC点阵杆件的几何形状最优参数值如表4所示,其对应的变截面FCC点阵的剪切模量较相应的等截面点阵提升了9.62%。如图4所示,是目标函数的迭代收敛曲线,整个优化迭代过程收敛平稳,目标函数最终收敛于0.037 11。

表3 剪切模量最大化的变截面点阵优化结果Tab.3 Optimization results of variable cross-section lattice for maximizing shear modulus

表4 变截面FCC点阵杆件截面几何形状最优参数值 (f=0.1)Tab.4 Optimum parameter values of cross-section geometry of FCC lattice bar with variable cross-section (f=0.1)

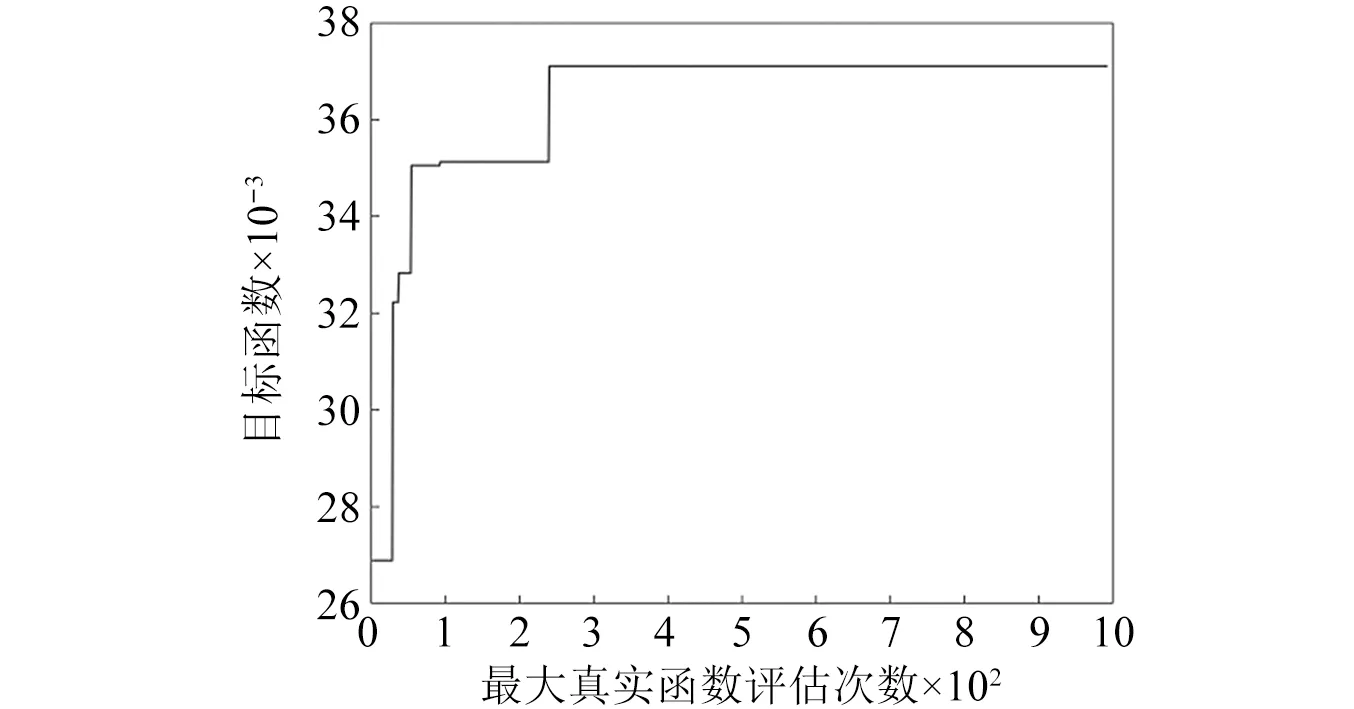
图4 材料用量约束为0.1时,变截面FCC点阵的目标函数收敛曲线Fig.4 Convergence curve of objective function of FCC lattice with variable cross-section when the material dosage constraint is 0.1

上述数值算例结果表明,相较于等截面点阵,在相同材料用量下,优化后的变截面点阵的体积模量或剪切模量可获得5% ～ 8%的力学性能提升效果。这主要得益于构建的变截面点阵几何显式描述模型,突破了传统点阵的等截面形状约束,实现了点阵几何形状的自由描述,扩大了基于近似模型辅助的粒子群优化算法的寻优空间。上述结果和分析也进一步验证了本文所提的变截面点阵结构优化设计方法的有效性和优势。

6 结 论

(1)本文基于近似模型辅助的粒子群优化算法提出了一种变截面点阵结构设计方法,基于显式拓扑描述模型,实现了变截面点阵几何形状的自由描述,基于能量均匀化方法建立了变截面点阵宏观等效弹性张量关于其几何描述参数的近似响应模型,并建立了变截面点阵几何描述参数的优化数学模型,采用基于近似模型辅助的粒子群优化算法实现上述优化模型的高效求解。数值算例表明,相较于等截面点阵,在相同材料用量下,优化后的变截面点阵具有更优异的力学性能。

(2)构建了基于显式拓扑描述函数的变截面几何描述模型,突破了传统点阵的等截面形状约束,实现了点阵几何形状的自由描述,为后续的智能优化算法提供了充分的寻优空间。

(3)建立了变截面点阵几何描述参数关于其宏观等效弹性张量的近似响应模型,并以此构建了变截面点阵几何描述参数的优化数学模型,引入基于近似模型辅助的粒子群优化算法,进一步提高了优化求解效率。

(4)本文以BCC,FCC,BCC+FCC三种代表性点阵构型验证了所提方法的有效性,但所提方法同样适用于其他任意构型的变截面点阵设计;同时本文仅研究了变截面点阵单胞的固有力学属性,可在本文研究基础上进一步考虑结构高承载、强减/隔振等多功能属性的变截面点阵单胞设计。