局部有限寿命疲劳约束条件下的结构拓扑优化方法

江旭东, 武子旺, 滕晓艳

(1. 哈尔滨理工大学 机械动力工程学院,哈尔滨 150080;2. 哈尔滨工程大学 机电工程学院,哈尔滨 150001)

面向金属增材制造的结构拓扑优化技术极大地丰富了工程结构的设计空间,兼顾了复杂结构和高性能构件成形需求,在航空、航天、交通、核电等领域具有广阔的应用前景和发展空间[1-2]。目前,多数的拓扑优化研究工作专注于体积约束下的结构刚度最大化问题,而工程结构往往服役于交变载荷作用的工作环境,刚度最优的设计一般不能完全满足抗疲劳要求,从而严重影响结构在全寿命周期内运行的可靠性。为此,在结构的轻量化设计中考虑疲劳性能约束,对丰富工程结构强度设计理论、提高服役性能有着重要的科学价值和工程意义。

为了抑制应力集中和高应力值引起的结构断裂,应力约束下的拓扑优化问题引起了高度的关注。应力约束拓扑优化设计的难点在于大量局部约束增加了敏度分析的计算代价。为了减少应力约束数量,一般采用P范数[3-5]和K-S函数[6]等凝聚方法将局部应力约束转化为一个全局约束。为了保持应力约束的局部性本质,代替上述函数凝聚技术,Silva等[7-9]利用增广拉格朗日方法,将多约束问题转化为一系列无约束子问题,求解了局部应力约束的拓扑优化问题。最近,Oliver等[10]将非结构化多边形网格技术[11]与增广拉格朗日方法相融合,提出了适用于复杂边界工程结构的局部应力约束拓扑优化设计方法。与应力约束拓扑优化问题不同,疲劳失效与加载历史具有强相关性,局部特征更为显著,导致疲劳约束拓扑优化问题呈现高度非线性,因而相关研究工作相对较少。研究学者利用Palmgren-Miner[12-14]、修正的Goodman[15-16]、Sines[17]及考虑初始缺陷的Murakami[18]等疲劳失效准则,结合准静态分析法[19-20]、频域[21-23]或时域等效静载荷等动态分析法[24-25]预测结构疲劳损伤,通过P范数方法凝聚疲劳约束,初步提出了考虑疲劳性能的连续体结构拓扑优化设计方法。尽管P范数方法能够大幅减少疲劳约束及其敏度分析的计算成本,但是其近似属性并不能精确地控制疲劳约束。

由此,本文基于增广拉格朗日方法提出局部疲劳约束问题的拓扑优化框架。考虑变幅比例载荷作用,通过Palmgren-Miner疲劳准则评定结构的疲劳损伤,以材料用量为目标函数,以疲劳性能为约束条件,提出基于局部疲劳约束的结构轻量化设计方法。此外,将非结构化多边形网格技术融入到拓扑优化模型,实现复杂几何边界结构的抗疲劳拓扑优化设计。对比现有P范数方法的优化结果,验证提出的非凝聚方法处理疲劳约束拓扑优化问题的有效性。

1 优化模型

在本文提出的拓扑优化框架内,以结构轻量化为目标,分别求解非凝聚的局部疲劳约束问题(Q1)和P范数凝聚的全局疲劳约束问题(Q2),对比分析两个问题的优化解,验证提出方法的有效性。

(1)

1.1 疲劳失效分析

为了估计变幅比例载荷作用下结构的高周疲劳损伤,本文通过雨流计数法确定多轴应力状态下的平均应力和应力幅,采用Sines准则评估疲劳等效应力,最后基于Palmgren-Miner线性累积损伤模型评估结构的疲劳失效。工程结构高周疲劳一般表现为低应力失效,因而可采用线性准静态分析法,通过线性叠加参考载荷下的结构响应,获得变幅载荷作用下的结构疲劳响应。

基于修正的固体各向同性材料惩罚模型(solid isotropic material with penalization,SIMP),材料插值函数mE[y(z)]表示为[26]

mE[y(z)]=ε+(1-ε)mV[y(z)]p

(2)

(3)

式中:Ersatz数ε≪1;p为惩罚因子;mV[y(z)]为Heaviside投影体积插值函数;α为门槛密度;η为投影控制参数。

为了加强优化问题的适定性,在规范化映射下将设计变量函数与线性“帽子”核函数卷积[27],使单元密度变量与设计变量具有如下关系

y=Pz

(4)

(5)

(6)

式中:P为过滤矩阵;R为过滤半径; ‖x-xk‖2为单元与k形心位置矢量x,xk的欧式距离;q为滤波指数。

为了能够求解具有复杂设计域结构的拓扑优化问题,利用非结构化多边形网格技术离散空间设计域,如图1所示,对于n边形参考单元,其节点i处的Wachspress形函数定义为

图1 多边形单元Fig.1 Polygon element definition

(7)

(8)

式中:αi(ξ)为插值函数;ξ=[ξ1ξ2]为n边形单元的内点;Ai(ξ),Ai+1(ξ)为相应阴影三角形的面积(如图1(a)所示),可根据式(9)计算获得

(9)

式中,pi-1=[p1,i-1p2,i-1]和pi=[p1,ip2,i]为n边形单元的相邻节点位置矢量。

考虑如图2所示的变幅载荷作用,采用准静态分析法求解结构在参考载荷下的疲劳响应,则有

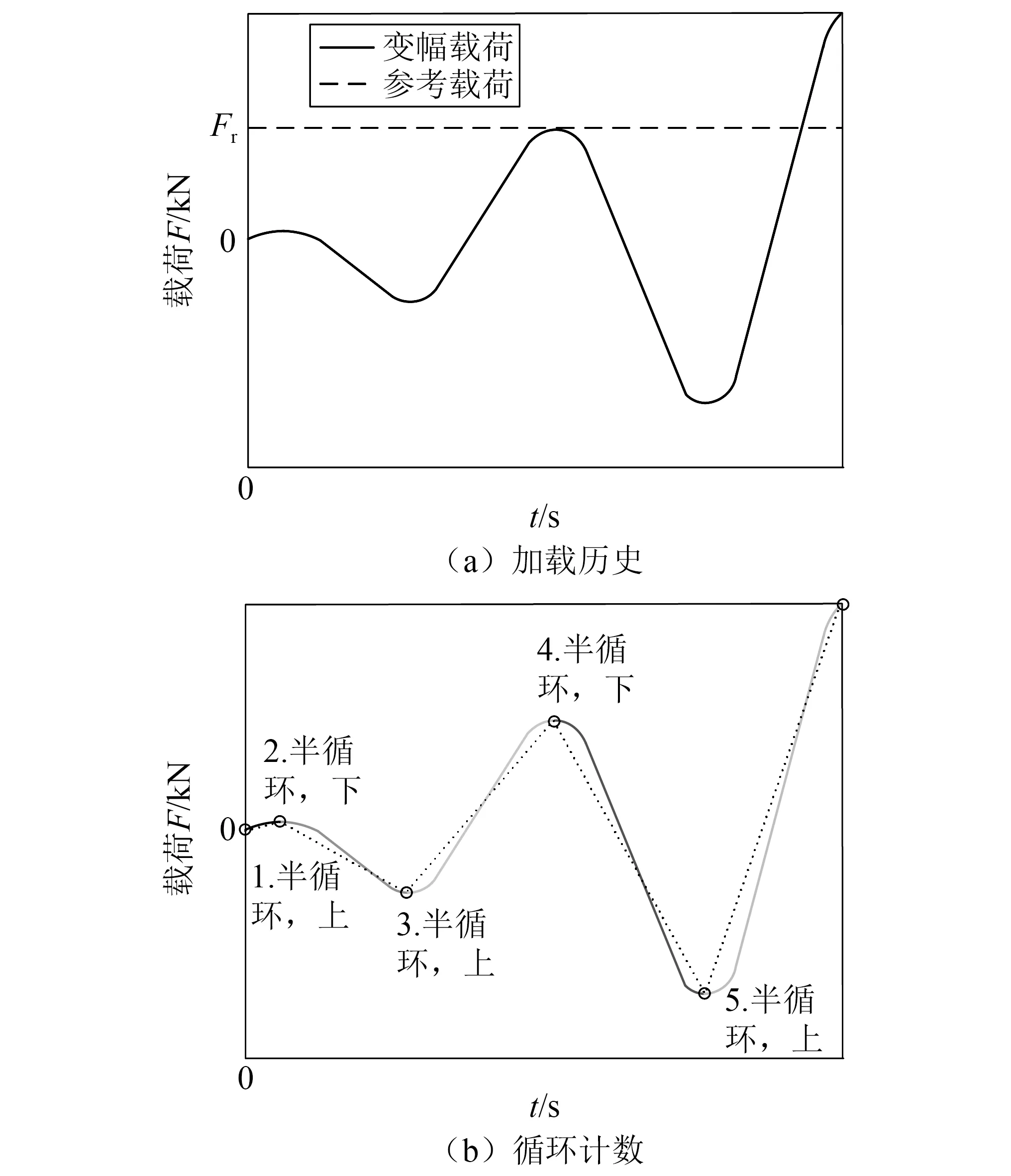
图2 雨流计数法Fig.2 Rainflow-counting method

K[y(z)]u=Fr

(10)

(11)

式中:K[y(z)]为结构插值总体刚度矩阵;Ke0为密度变量为1时的单元刚度矩阵。

为了避免优化问题的奇异解现象,采用修正的qp松弛技术处理单元应力。对于无预应力的线弹性结构,参考载荷作用下的单元参考应力表示为

(12)

为了预测工程结构在变幅载荷下的疲劳损伤,往往通过雨流计数法从应力谱中提取峰值与谷值(见图2),确定不同循环特征的应力循环,由此获得应力幅缩放因子与平均应力缩放因子,根据式(13)估算任一应力循环的应力状态。

(13)

式中:σea,i,σem,i分别为单元e在第i个循环的应力幅和平均应力列阵;cai,cmi分别为第i个循环的应力幅和平均应力缩放因子。

根据Sines有限寿命疲劳准则,平面应力状态下有限寿命的等效单轴应力可由交变的八面体剪切应力和静水平均应力依据式(14)获得[28]

(14)

Basquin方程描述了单轴等效应力与疲劳寿命的关系,表示为

(15)

式中:σf为疲劳强度系数;Nei为应力循环i下结构的疲劳寿命;b为疲劳强度指数。

由此,根据式(14)、式(15),采用Palmgren-Miner线性累积损伤模型可以评定整个载荷谱作用下的任一单元的疲劳损伤,工程结构须满足如下疲劳约束,方能避免疲劳断裂发生。

(16)

式中:De为单元e的累计损伤;cD为缩放参数(一般大于1);ni为载荷循环i的循环次数;nRF为不同应力循环特征的组合总数。

1.2 疲劳约束

对于优化问题Q2, P范数疲劳约束可表示为

(17)

式中,P为P范数因子。

高的P范数因子有利于估计函数的最大值,但是,也会增加优化问题的非线性,不利于问题求解和造成收敛困难。为了使P范数损伤靠近实际损伤的最大值,一般采用自适应约束缩放技术[29]修正P范数损伤。

(18)

如图3所示,多项式约束函数式(18)在约束违背域的惩罚幅度远大于线性约束函数,而在Λj≈0处类似于传统线性约束。尽管式(18)的立方项增加了疲劳约束的非线性,但是,数值试验表明:相对于线性约束函数,对疲劳约束违背域施加非线性惩罚能够驱动优化解更加快速地向低损伤方向迭代。

图3 传统线性约束与三次方约束的比较Fig.3 Comparison between traditional linear and cubic constraints

1.3 敏度分析

依据链式求导法则,优化问题Q1的目标函数对于设计变量的灵敏度为

(19)

根据优化问题式(1),目标函数对于材料插值函数和体积插值函数的偏导数为

(20)

给定材料刚度参数E=mE(y)和体积分数V=mV(y),它们对于设计变量的偏导数为

(21)

多项式疲劳性能约束对于设计变量的灵敏度表示为

(22)

由式(18),多项式疲劳性能约束对于材料插值函数和体积插值函数的偏导数为

(23)

(24)

(25)

根据Palmgren-Miner线性累积损伤模型式(16)和式(15),损伤变量与疲劳寿命的偏导数分别为

(26)

将式(12)代入式(13),可获得应力幅列阵和平均应力列阵的偏导数,表示为

(27)

(28)

(29)

2 增广拉格朗日方法

图4 增广拉格朗日优化框架流程图Fig.4 Schematic flowchart of the AL-based topology optimization framework

当单元的数量足够大时,惩罚项P(k)(z,u)可能远大于目标函数f(z),从而引起算法失效。由此,引入归一化的惩罚项[31]避免优化问题的奇异性,则归一化的拉格朗日子问题表示为

(30)

(31)

(32)

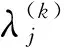
μ(k+1)=min[αμ(k),μmax]

(33)

式中:α>1为惩罚因子更新参数,上确界μmax用于抑制算法的数值失稳问题。拉格朗日乘子按照式(34)更新

(34)

基于梯度的全局收敛移动渐近线算法[32](globally convergent method of moving asymptotes, GCMMA)具有较好的稳定性和鲁棒性,本文采用GCMMA求解上述疲劳约束拓扑优化问题。按照链式求导法则,归一化的拉格朗日目标函数的灵敏度为

(35)

由式(31),P(k)与体积分数V不直接相关,而通过局部疲劳性能约束与刚度参数E相关,它对于上述参数的偏导数为

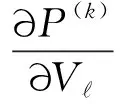
(36)

(37)

对于变幅载荷作用的多工况问题,伴随方法可有效求解优化问题式(30)的灵敏度。将参考载荷(分解为应力幅载荷与平均应力载荷)作用下的平衡方程以残差形式引入到式(37)中,形成增广形式的惩罚项敏度分析方程,则有

(38)

Rai=Kuai-Fr,ai=0,Rmi=Kumi-Fr,mi=0

(39)

式中:Rai,Rmi分别为应力幅和平均应力平衡方程的残差表达式;ξai,ξmi为相应的伴随矢量。

将式(39)对材料刚度参数求偏导数,则有

(40)

观察式(38),随着应力循环数的增加,伴随矢量的计算将消耗大量的时间。因而,通过式(41) 缩放参考载荷作用下的位移,表示任意循环载荷作用下的幅值位移与平均位移,可以有效缩减伴随矢量的解算规模。

uai=caiu,umi=cmiu

(41)

由此,式(38)的伴随项表示为

(42)

另外,为了避免直接求解∂u/∂E,通过合理选择伴随矢量满足式(43),使其在式(42)中消失,则有

(43)

由此,确定所有缩放的伴随矢量后,结合式(44)则可获得惩罚项对于刚度参数的偏导数。

(44)

(45)

(46)

最后,由式(12)和式(13),∂σea,i/∂u和∂σem,i/∂u可显式获得,表示为

(47)

综上,编制有限寿命疲劳分析的多边形有限元计算程序、敏度分析程序、设计变量滤波程序与GCMMA求解器,实现局部有限寿命约束条件下的结构优化。

3 结果与讨论

3.1 L型板

如图5所示,L型支架的尺寸参数L=1 m,弹性模量E0=70 GPa,泊松比μ=0.3,疲劳强度系数σf=1 350 MPa,疲劳强度指数b=-0.086。L型支架上端施加固定约束,右侧角点施加横向变幅载荷F(见图2),其参考载荷Fr=20 kN。过滤半径R=0.065,惩罚因子p=3,门槛密度α=0.5,投影控制参数η=2～10(增量为0.7,更新频率为5)。

图5 L型支架设计域与边界条件Fig.5 Design domain and boundary conditions for a L-bracket

设计域离散为N=50 176个单元,横向载荷施加于垂向棱边的8个单元上,避免在加载区域的应力集中。上述单元不包含在设计域中,它们的密度变量设置为1。施加随机载荷Pk=rand(Fr,-Fr),其中k=1 000,载荷谱缩放参数cD=750。图6为L型支架采用P范数凝聚方法(P范数因子P=8)和非凝聚方法获得的优化拓扑及损伤分布。对比两种方法的分析结果,尽管设计构型存在一定的相似性,但是,局部约束作用的优化拓扑在载荷施加区域附近具有更加合理的结构形式,结构拓扑接近于等强度设计,因而材料的抗疲劳性能得到充分利用。另外,从材料用量来看,P范数凝聚方法的目标值为0.305,非凝聚化方法的目标值为0.252,后者质量减轻17.4%,验证了所提方法的有效性。

图6 L型支架的优化拓扑与损伤分布Fig.6 Optimal topology and damage distribution for a L-bracket

3.2 天线支架

如图7所示,天线支架的尺寸参数L=4 m,H=6 m,弹性模量E0=120 GPa,泊松比μ=0.3,疲劳强度系数σf=1 350 MPa,疲劳强度指数b=-0.086。天线支架左端施加固定约束,右侧角点施加横向变幅载荷F(见图2),其参考载荷Fr=400 kN。过滤半径R=0.06,惩罚因子p=3,门槛密度α=0.5,投影控制参数η=2～10(增量为1.0,更新频率为5)。

图7 天线支架设计域与边界条件Fig.7 Design domain and boundary conditions for an antenna bracket

设计域离散为N=50 000个单元,横向载荷施加于斜向棱边的8个单元上,避免在加载区域的应力集中。上述单元不包含在设计域中,它们的密度变量设置为1。施加随机载荷Pk=rand(Fr,-Fr),其中k=1 000,载荷谱缩放参数cD=30 000。图8为天线支架采用P范数凝聚方法(P范数因子P=10)和非凝聚方法获得的优化拓扑及损伤分布。对比两种方法的分析结果,局部约束作用的优化拓扑改变了内部加强筋的布局,使得在P范数约束优化拓扑中高损伤区域处的疲劳损伤有所下降,导致更少的单元承受疲劳失效,因而具有更优的抗疲劳性能。另外,从材料用量来看,P范数凝聚方法的目标值为0.382,非凝聚化方法的目标值为0.256,后者质量减轻33.0%,有利于工程结构的轻量化设计。

图8 天线支架的优化拓扑与损伤分布Fig.8 Optimal topology and damage distribution for an antenna bracket

3.3 门式钢架

如图9所示,门式钢架的尺寸参数L=1.6 m,H=0.8 m,l=0.15 m,弹性模量E0=100 GPa,泊松比μ=0.3,疲劳强度系数σf=1 350 MPa,疲劳强度指数b=-0.086。门式钢架底端施加固定约束,上表面中心处施加横向变幅载荷F(见图2),其参考载荷Fr=70 kN。过滤半径R=0.035,惩罚因子p=4.5,门槛密度α=0.5,投影控制参数η=1～10(增量为3,更新频率为5)。

图9 门式钢架设计域与边界条件Fig.9 Design domain and boundary conditions for a portal frame

设计域离散为N=50 000个单元,横向载荷施加于上表面棱线中间的12个单元上,避免在加载区域的应力集中。上述单元不包含在设计域中,它们的密度变量设置为1。施加随机载荷Pk=rand(Fr,-Fr),其中k=1 000,载荷谱缩放参数cD=10 000。图10为门式钢架采用P范数凝聚方法(P范数因子P=10)和非凝聚方法获得的优化拓扑及损伤分布。对比两种方法的分析结果,局部约束作用的优化拓扑优化了载荷施加区域附近的传递路径,祛除了对于削弱疲劳损伤作用较小的冗余结构,最优拓扑图像结构清晰,传力路径明确,具有更优的抗疲劳性能。另外,从材料用量来看,P范数凝聚方法的目标值为0.286,非凝聚化方法的目标值为0.226,后者质量减轻21.0%,验证了所提方法的有效性。

图10 门式钢架的优化拓扑与损伤分布Fig.10 Optimal topology and damage distribution for a portal frame

3.4 圆孔矩形板

如图11所示,圆孔矩形板的尺寸参数L=1.2 m,H=0.4 m,D=0.24 m,弹性模量E0=100 GPa,泊松比μ=0.3,疲劳强度系数σf=1 350 MPa,疲劳强度指数b=-0.086。孔矩形板的左端施加固定约束,右端中心处施加横向变幅载荷F(见图2),其参考载荷Fr=15 kN。过滤半径R=0.05,惩罚因子p=4.5,门槛密度α=0.5,投影控制参数η=2～10(增量为0.7,更新频率为5)。

图11 圆孔矩形板设计域与边界条件Fig.11 Design domain and boundary conditions for a rectangular plate with circular holes

设计域离散为N=30 000个单元,横向载荷施加于右端垂向棱边的6个单元上,避免在加载区域的应力集中。上述单元不包含在设计域中,它们的密度变量设置为1。施加随机载荷Pk=rand(Fr,-Fr),其中k=1 000,载荷谱缩放参数cD=10 000。图12为圆孔矩形板采用P范数凝聚方法(P范数因子P=8)和非凝聚方法获得的优化拓扑及损伤分布。对比两种方法的分析结果,尽管设计构型存在一定的相似性,但是,局部约束作用的优化拓扑在传力路径上有效减少了冗余材料,使其与P范数凝聚的优化拓扑具有相近的疲劳损伤,因而具有更优的材料分布。另外,从材料用量来看,P范数凝聚方法的目标值为0.416,非凝聚化方法的目标值为0.386,后者质量减轻7.2%。与实体域结构相比,由于结构中增加的圆孔削弱了抗疲劳能力,导致可减少的材料用量受到限制。

图12 圆孔矩形板的优化拓扑与损伤分布Fig.12 Optimal topology and damage distribution for a rectangular plate with circular holes

3.5 圆孔曲线板

如图13所示,圆孔曲线轮廓板的尺寸参数L=2.8 m,D1=0.35 m,D2=0.6 m,R1=0.3 m,R2=0.5 m,弹性模量E0=100 GPa,泊松比μ=0.3,疲劳强度系数σf=1 350 MPa,疲劳强度指数b=-0.086。圆孔曲线轮廓板右端施加固定约束,左端圆孔施加均布横向变幅载荷F(见图2),其参考载荷Fr=10 kN。过滤半径R=0.03,惩罚因子p=3,门槛密度α=0.5,投影控制参数η=1～10(增量为3,更新频率为5)。

设计域离散为N=30 000个单元,横向均布载荷施加于左侧圆孔下方所有单元上。上述单元不包含在设计域中,它们的密度变量设置为1。施加随机载荷Pk=rand(Fr,-Fr),其中k=1 000,载荷谱缩放参数cD=11 000。图14为圆孔曲线轮廓板采用P范数凝聚方法(P范数因子P=10)和非凝聚方法获得的优化拓扑及损伤分布。对比两种方法的分析结果,考虑局部约束作用的优化拓扑在两圆孔间增加了多条加强筋,有效地阻碍了疲劳损伤的传递,使得P范数凝聚方法的高损伤区域转变为中度损伤区域,提高了结构的抗疲劳性能。另外,从材料用量来看,P范数凝聚方法的目标值为0.258,非凝聚化方法的目标值为0.228,后者质量减轻11.6%,验证了所提方法的优越性。

图14 圆孔曲线轮廓板的优化拓扑与损伤分布Fig.14 Optimal topology and damage distribution for a curved plate with circular holes

4 结 论

(1) 针对变幅载荷作用下的高周疲劳结构的轻量化问题,利用Palmgren-Miner损伤准则在有限单元上逐一构建多项式局部疲劳性能约束,避免任意材料评估点处的疲劳失效;同时,基于增广拉格朗日方法将原问题转化为一系列无约束优化子问题,有效地解决了拓扑优化问题中的大量局部约束所带来的挑战。

(2) 与疲劳约束凝聚化的优化结果相比,局部疲劳约束条件所获得的设计构型与其具有很大的差异,优化结构的疲劳损伤和材料用量都显著减小,因而考虑局部疲劳约束有益于材料的充分利用和结构抗疲劳性能的改善。

(3) 与现有的基于单元的疲劳问题拓扑优化方法相比,本文采用非结构化的多边形有限元法完成连续体结构的疲劳分析与损伤评估,能够实现具有任意曲线边界设计域结构的拓扑优化设计。

综上,所提方法为实现考虑疲劳性能约束的连续体结构的轻量化设计提供了一种新的思路。未来工作将以本文为基础,考虑惯性和阻尼效应的影响,研究动态载荷作用下结构疲劳约束问题的设计优化。