数学核心素养测评之过程领域分析

胡典顺 张静

胡典顺

华中师范大学数学与统计学学院教授、博士研究生导师，华中师范大学数学教育教研室主任，湖北省中学数学教学指导委员会副主任委员；《数学教育学报》《数学通讯》编委，鄂教版高中数学教材（2019年版）副主编，中国国际文化交流基金会第三届“明德教师奖”获得者；曾以访问学者的身份，由国家留学基金委公派访问美国特拉华大学；在《课程·教材·教法》《中国教育學刊》《数学教育学报》《教育科学研究》等期刊上发表论文270余篇，出版《基于数学意义的数学教学改革研究》《整合技术的学科教学知识：从教师专业素养到教师教学实践》《中学生数学素养测评的模型建构与实证研究》等专著，主持多项全国教育科学规划项目和教育部人文社会科学研究规划基金项目。

数学核心素养测评从内容领域、情境领域、过程领域、核心素养领域四方面对学生的数学素养进行分析。在数学核心素养测评中设置过程领域测评维度，是为了考查学生将真实情境中的问题数学化，建立数学表征，运用数学概念、方法和推理等获得数学结论，并阐述数学结论的能力。本文基于“WJ市义务教育核心素养监测”项目，阐述过程领域的内涵及其测评分析过程和结果。

一、过程领域的内涵

“数学过程”指数学概念、公式、定理、法则等的提出过程，数学结论的形成过程，数学思想方法的探索及概括、总结过程，以及运用数学的过程等。其本质是以“抽象—符号变化—应用”为核心的思维过程。本项目中，笔者基于国际PISA测试框架，依据个体解决数学问题的步骤，将数学过程划分为表述、运用和阐释三个维度。

这三个维度分别描述了个体将现实问题与数学相连接的过程、解决数学问题的过程和对数学结果进行交流、评判的过程。具体地讲，“表述”指数学化（公式化、系统化）地表述情境，即将现实情境转化为数学情境，利用数学结构陈述现实问题，以便于理解数学现象；“运用”指数学概念、事实、程序和原理等的运用，即在具备一定的数学知识和分析、建模能力的基础上，运用数学概念、方法和推理等获得数学结论，解决现实问题；“阐释”指解释、应用和评价数学的结果，即在现实情境中解释数学结果，并对结果进行评判。

二、测评分析过程和结果

1.学生表现情况分析

为便于对过程领域学生表现的差异进行量化分析，笔者基于3544份有效数据，将学生在“表述、运用、阐释”三个维度的成绩分别加权成百分制，并利用SPSS26.0进行描述性统计，得出学生在三个维度的成绩最小值均为“0”、最大值均为“100”，均值依次下降，分别为85.935（表述）、73.026（运用）、61.943（阐释）。这说明学生擅长结合实际解释数学结果，但运用数学知识解决实际问题的能力较弱。

同时，笔者利用SPSS26.0分别计算7个区（县）学生在三个维度的成绩均值及得分率，进一步整理得到下表，以对比各区（县）学生在过程领域的素养表现。

根据表1中的数据，笔者绘制如下过程领域各区（县）学生得分率折线图。

观察上图，纵向比较可知，各区（县）学生在表述维度的得分率最高，在运用维度次之，在阐释维度最低；横向比较可知，三个维度中，区（县）2［即编码为02的区（县），下同］、区（县）6、区（县）7的学生得分率排名均在前三名，区（县）3的学生得分率排名均为最后一名。这说明学生在过程领域的成绩存在地域差异，但表现相对稳定。

2.学生表现水平分析

为进一步分析学生在三个维度表现水平分布的差异，特别是精熟度水平较高的学生与精熟度水平较低的学生在这三个维度分布的差异，笔者将三个维度的学生成绩按照统一标准进行了精熟度水平划分。

根据等级划分原则，笔者对学生的测试总分进行等级划分。首先，笔者从测试评分框架中删除最高的5%学生成绩与最低的5%学生成绩，即第5百分位之前和第95百分位之后的成绩不纳入测评分析的范围。利用SPSS26.0统计第5百分位和第95百分位成绩的步骤如下：选择【分析】→【描述统计】→【频率】，将“表述［ES］”“运用［AY］”“阐释［EN］”放入【变量】对话框；选中【统计】，勾选【百分位数】，添加“5”“95”，点击【继续】→【确定】。由此得出表述维度的第5百分位数为48、第95百分位数为100，运用维度的第5百分位数为26、第95百分位数为97，阐释维度的第5百分位数为17、第95百分位数为88。

然后，笔者根据前期文章介绍的精熟度水平区间计算方法，得出三个维度的学生成绩等级分布，并统计每个区间学生成绩的频数，计算百分比。以表述维度下分数分布在0～48分的学生人数统计为例，具体步骤如下：选择【数据】→【选择个案】，勾选【如果条件满足】→【如果】，将“表述［ES］”放入对话框，输入“ES<=48”，点击【继续】；勾选【将选定个案复制到新数据集】，并将数据集命名为“等级0”，点击【确定】。这样得出表述维度下分数分布在0～48分的学生成绩数据集，以及该区间学生成绩的频数。笔者按照以上步骤操作7次，整理统计结果，得到如下表述维度的等级分布表。

同样地，笔者按照上述方法得出运用维度和阐释维度的等级分布表，明确了运用维度分数分布（0～26分为0级，27～39分为1级，40～52分为2级，53～65分为3级，66～78分为4级，79～91分为5级，92～100分为6级）和阐释维度分数分布（0～17分为0级，18～30分为1级，31～43分为2级，44～56分为3级，57～69分为4级，70～82分为5级，83～100分为6级），以及学生成绩在各区间的频数（运用维度各区间成绩频数分别为170、151、237、309、802、1238、637；阐释维度各区间成绩频数分别为174、172、240、440、1030、964、524）和百分比（具体数据见下图）。

为更好地研究学生成绩在三个维度的精熟度水平分布差异，笔者绘制如下过程领域等级分布百分比条形图。

从上图可知，表述维度的精熟度水平处于0～3级的学生占比均在5%～11%之间，处于4～6级的学生占比达到77.2%，其中，6级的学生占比最多，高达34.8%，说明绝大部分学生已经掌握了数学表述的方法；运用维度的精熟度水平处于0～3級的学生占比均在4%～9%之间，处于4～6级的学生占比达到75.5%，其中，5级的学生占比最多，为34.9%，说明学生在数学运用方面两极分化不明显，中上等级学生人数相对比较均衡，大部分学生具备良好的数学运用能力；阐释维度的精熟度水平处于0～3级的学生占比均在4%～13%之间，处于4～6级的学生占比达到71.1%，其中，4级的学生占比最多，为29.1%，6级的学生占比最少，仅为14.8%，说明在数学阐释方面，学生的表现较好，处于中等水平的学生占比相对较高，但能够熟练掌握数学阐述的学生不多。

3.过程领域相关分析

为了研究学生在表述、运用、阐释三个维度的成绩是否会相互影响，笔者利用SPSS26.0对学生三个维度的成绩进行皮尔逊相关分析，具体步骤如下：选择【分析】→【相关】→【双变量】，将“表述［ES］”“运用［AY］”“阐释［EN］”放入【变量】对话框；勾选【皮尔逊】【双尾】【标记显著性相关性】，点击【确定】。运行结果如表3所示。

从表3可知，表述维度和运用维度的皮尔逊相关系数约为0.688，表述维度和阐释维度的皮尔逊相关系数约为0.644，运用维度和阐释维度的皮尔逊相关系数约为0.798。这说明三个维度的学生表现两两正相关，且显著性均小于0.01。其中，运用维度和阐释维度的皮尔逊相关系数最高，说明这两个维度的成绩之间关系更密切。

4.过程领域差异性分析

过程领域中，办学类型（小学、九年一贯制学校、十二年一贯制学校）、学校举办者类型（教育部门、民办）、学校所处位置（城市、县镇、农村）等因素对学生成绩的影响，是有价值的差异性分析。受篇幅所限，下面仅展示过程领域学生成绩与办学类型的差异性分析过程及结果。

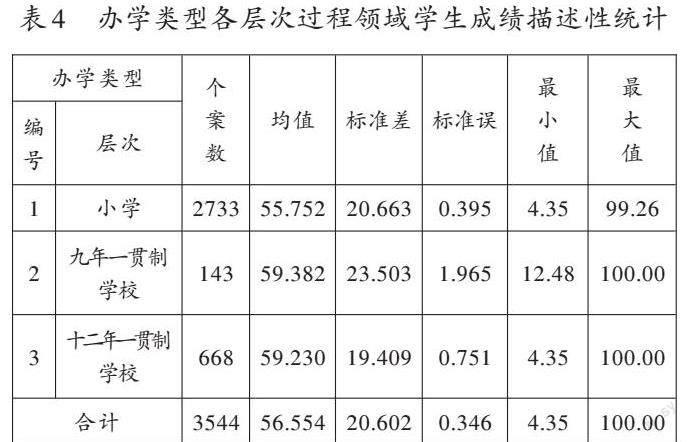
笔者利用SPSS26.0对学生的过程领域成绩总分的均值、标准差、标准误等进行描述性统计分析，得到如表4所示的结果。

由表4可知，所有的学生在过程领域学生成绩这个背景指标上的平均分为56.554分，九年一贯制学校、十二年一贯制学校的得分均值高于平均分，且九年一贯制学校的得分均值最高（59.382分），而小学的得分均值（55.752分）低于平均分。结果表明，不同办学类型的学生成绩均值之间存在一定的差异。

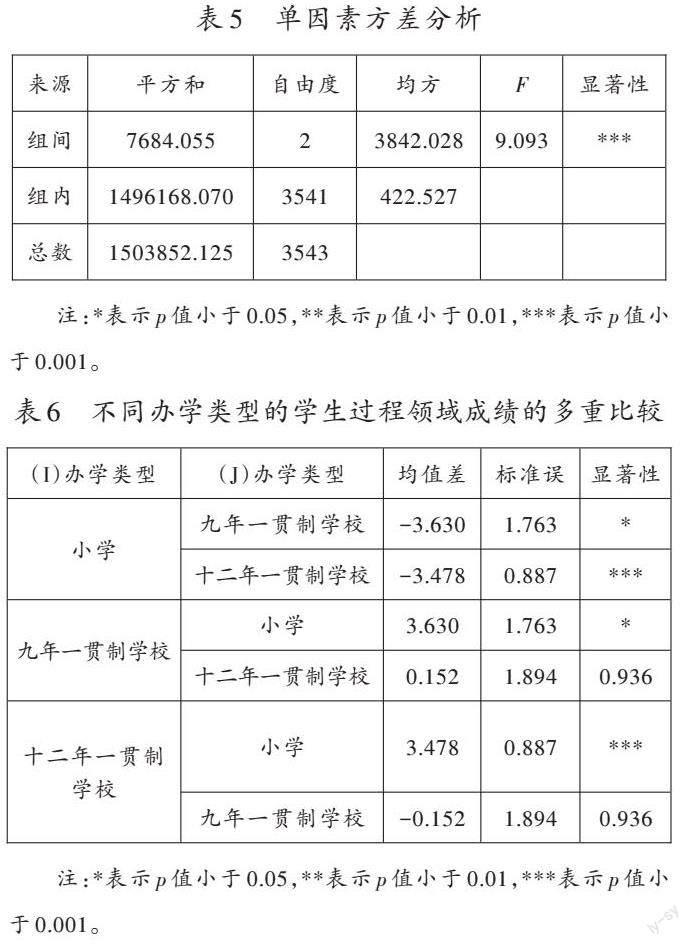
为进一步检验不同办学类型的学生成绩均值之间是否存在显著性差异，笔者利用SPSS26.0在0.05的水平上做单因素方差分析以及LSD多重比较分析，具体步骤如下：选择【分析】→【比较平均值】→【单因素ANOVA检验】，将“q”（过程领域的学生成绩总分）放入【检验变量】对话框，将“办学类型[type]”放入【因子】对话框；点击【事后比较】，勾选【LSD】，点击【继续】→【确定】。运行结果如表5、表6所示。

由表5可知，组间F值为9.093，p值小于0.001，从而拒绝原假设，表明不同办学类型学校学生的过程领域成绩之间存在显著性差异。笔者根据表6进一步确定三个办学类型中两两之间的差异性，结果表明：在小学与九年一贯制学校的两两比较中，显著性小于0.05，说明两者存在显著性差异；在小学与十二年一贯制学校的两两比较中，显著性小于0.001，说明两者存在显著性差异；在九年一贯制学校与十二年一贯制学校的两两比较中，显著性大于0.05，说明两者不存在显著性差异。

（张静系华中师范大学数学与统计学学院硕士研究生）

责任编辑  刘佳