计及长短周期混合储能的多能微网能量-功率分布鲁棒优化

赵 波，王文博，陈 哲，罗冰洋，李志浩，汪湘晋

（1.国网浙江省电力有限公司电力科学研究院,浙江省杭州市 310014；2.武汉理工大学自动化学院,湖北省武汉市 430070）

0 引言

多能微网作为一种集源、储、荷于一体的微型能源系统,通过内部调控可应对大量风光电源接入对配电系统带来的安全、稳定问题,进而提高配电网对分布式可再生能源的消纳能力和利用效率。随着微网技术的发展与可再生能源渗透率的提高,能量生产与消费将逐步呈现分布式与就地化趋势。因此,对多能微网的长周期（通常为1 星期）自治运行能力提出了更高要求［1-2］。但可再生能源固有的随机性、间歇性与波动性给多能微网的自治可靠运行带来了挑战。

储能作为一种灵活性调节资源,可平抑分布式可再生能源波动,促进消纳,在多能微网中扮演着重要角色［3-5］。然而,目前大多数储能技术如电池储能、抽水蓄能等的储能能力有限（持续时间约为2～10 h）,主要提供调峰、调频、爬坡备用等辅助功能,以平抑分布式能源短时间尺度功率波动,但无法解决长时间尺度下可再生能源与负荷之间的功率不平衡问题。随着电转氢（power to hydrogen,P2H）技术［6］的发展与应用,氢储能作为一种新型储能方式,受到了国内外学者的广泛关注［7-8］。氢储能利用富余电力通过电解水转化为氢气进行存储,并在电力不足时通过氢燃料电池消耗氢气进行发电。与电池储能、抽水蓄能等储能方式相比,氢储能在大规模、长时间的能量存储方面更具优势。因此,将电化学储能等短周期储能与氢储能等长周期储能协同应用,可有效提升多能微网的自治运行能力。

目前,已有一些学者在电氢混合储能协同方面做了相关研究。文献［9-10］在电力系统中应用氢储能来平抑可再生能源波动。文献［11］在上述基础上考虑了电热转化设备和电解水制氢设备启停约束,并将电、氢、热协同优化,分析了面向氢气和热能灵活供应的电-氢、电-热转化过程。文献［12-13］进一步建立了非线性模型,精确描述电-氢之间的相互转化过程。然而,上述文献中氢储能与电化学储能的平衡时间相同,无法发挥氢储能长周期能量存储的优势。文献［14］构建了一个包含氢储能（长期储能）与蓄电池（短期储能）的复合能源系统,并基于深度强化学习的方法进行能量协调控制。文献［15］在其基础上将长短周期混合储能微网与短周期储能微网进行经济性对比,验证了长短周期混合储能协同应用的优势。然而,现有研究大多基于单一时间尺度,特别是面向多能微网的自治运行需求,未能将周前等长周期调度方案与日前等短周期调度方案相协调,导致调度结果不经济或不可靠。

在可再生能源、负荷等不确定性因素建模方面,目前的建模方法主要包括基于场景的随机优化［16-17］和鲁棒优化［18-19］。然而,基于场景的随机优化需要采样大量场景,导致模型求解效率较低；鲁棒优化使用不确定集刻画不确定性,避免了场景采样,但获得的结果往往过于保守。分布式鲁棒优化（distributionally robust optimization,DRO）算法［20］将随机优化与鲁棒优化相结合,通过寻找已知置信区间内离散场景的最恶劣概率分布值,在保障系统鲁棒性的同时降低了运行方案的保守性。然而,传统使用Wasserstein 距离度量［21］构建概率分布集合将导致NP 难问题,优化求解方法较为复杂。为了解决这一问题,文献［22-24］通过数据驱动的方法对大量不确定性场景历史数据进行聚类,通过1-范数和∞-范数对离散场景概率分布进行约束,从而避免表征矩信息的对偶化,降低了算法的求解难度。然而,上述研究均是基于单独的1-范数约束或∞-范数约束进行分析,优化结果相对片面。实际应用时,须对比1-范数约束和∞-范数约束来给出调度方案,影响模型求解效率。同时,基于强对偶理论将max-min 双层子问题转化为单层max 形式的求解方法,无法直接应用于混合整数规划问题。

综上所述,针对现有研究的不足,本文提出了一种计及长短周期混合储能协同应用的多能微网能量-功率分布鲁棒优化匹配方法。基于长周期能量平衡模型与短周期功率平衡模型滚动优化的方式,统筹考虑长短周期源荷匹配,提升了微网的自治运行能力。其中,在日前优化阶段,建立了基于数据驱动的两阶段分布鲁棒优化模型以刻画源荷双侧不确定性,综合1-范数和∞-范数对不确定性场景概率分布进行约束,得到唯一的调度方案,保证了微网的鲁棒性和经济性。采用列与约束生成（column and constraint generation,C&CG）算法对日前优化模型并行求解,并通过算例分析验证了该方法的经济性和有效性。

1 微网能量-功率分布鲁棒优化

多能微网包括电、氢、热3 种能源系统,其结构如附录A 图A1 所示。以电储能、热储能与氢储能混合储能方式提供系统备用,以P2H 装置、氢燃料电池、热回收装置和电热装置为耦合元件,构成了电、氢、热3 种能源相互流动的多能微网。

针对多能微网内可再生能源与负荷长时间尺度预测误差较大的问题,本文基于长短周期混合储能建立了能量-功率匹配滚动优化模型,如附录A 图A2 所示。长周期能量平衡模型根据微网的自治运行需求,设调度周期为I日,调度间隔为1 日。长周期能量平衡模型以调度周期内可再生能源与负荷的长时间尺度预测值为基础,以最小化能量调度成本为目标,确定调度周期内微网的能量调度策略,并提供当日短周期功率平衡模型燃油消耗总量和储氢总量约束。短周期功率平衡模型调度周期为24 h,调度间隔为1 h,以可再生能源与负荷日前24 h 预测数据为基础,以最小化功率调度成本为目标,确定24 h内微网运行策略。实时调度模型的调度周期为1 h,调度间隔为15 min,基于可再生能源与负荷的实时数据,调动微网日前运行策略的备用能源,确定系统实际调度策略并返回当日实际燃油消耗量与储氢量,修正下一阶段能量平衡模型初始状态,实现系统能量-功率匹配滚动优化。

1.1 长周期能量平衡模型

由长周期能量平衡模型的调度周期与调度间隔可知,系统需进行I次长周期能量平衡调度,第i次调度模型描述如下。

1）目标函数

式中:Ci为第i次调度总成本；COi,t、CHi,St、CLi,Ot分别为第i次长周期能量平衡调度第t日传统发电机所消耗的燃油成本、氢储能设备储能成本和系统弃风/弃光惩罚成本。

2）能量平衡约束

长周期能量平衡模型的能量平衡约束如下:

式中:EGEi,t为发电机发电量；EPVi,t和EPWi,t分别为光伏和风电的实际发电量；EFCi,t为氢燃料电池装置发电量；ELi,t为电负荷；EPi,2tH为P2H 装置消耗能量；EWi,t为电热装置消耗能量；HP2Hi,t为P2H 装置的产氢量；Hchi,t和Hdisi,t分别为氢储能装置充氢量和放氢量；HLi,t为氢负荷；HFCi,t为氢燃料电池消耗的氢量；WRi,t为热回收装置回收的热量；WEi,t为电热装置生成的热量；为热负荷。

3）传统发电机模型

传统发电机成本函数可表示为:

式中:CO为燃油发电机的成本系数；Oi,t为第i次长周期能量平衡调度第t日发电机消耗的燃油量。

微网采取自治运行策略,传统发电机在一个调度区间内的耗油量应小于该地区在这段时间的储油量。因此,出力需要满足如下平衡约束:

式中:O0为第i次长周期能量平衡调度燃油初始储存量；τ为传统发电机燃油发电的转换效率；EGEmax为传统发电机一日内发电总量的上限。

4）可再生能源模型

可再生能源弃电成本包括弃风、弃光两部分,其成本函数为:

式中:CLV为弃光惩罚系数；CLW为弃风惩罚系数；NPV为光伏发电机数量；NPW为风力发电机数量；EPVi,t,f和EPWi,t,m分别为第i次长周期能量平衡调度中第t日第f台光伏发电机、第m台风力发电机的产能实际值；EPV,yi,t,f和EPW,yi,t,m分别为第i次长周期能量平衡调度中第t日第f台光伏发电机、第m台风力发电机的产能预测值。

可再生能源出力约束:

5）氢储能模型

氢储能装置成本函数可表示为:

式中:CHS为储氢成本系数；ηCH为氢储能装置储氢效率；ηDH为氢储能装置放氢效率。

氢储能装置出力约束可表示为:

式中:uHSi,t为0-1 变量,表示氢储能装置充放状态；Hi,t为第i次长周期能量平衡调度第t日氢储能装置储氢量；Hmin和Hmax分别为氢储能装置储氢总量的下限和上限；Hdismax和Hchmax分别为氢储能装置一日内放氢量和充氢量上限。

氢储能装置为长周期储能,其平衡约束为:

式中:H0为第i次长周期能量平衡调度氢储能装置初始储氢量；HI第i次长周期能量平衡调度氢储能装置最终储氢量。

6）P2H 装置模型

P2H 装置功率约束可表示为:

式中:ηP2H为P2H 装置转换效率；HP2Hmax为P2H 装置一日内产氢量上限。

7）氢燃料电池模型

式中:ηFC为氢燃料电池转换效率；EFCmax为氢燃料电池一日内发电量上限。

8）热回收装置模型

热回收装置出力约束可表示为:

式中:ηRP2H为热回收装置回收P2H 装置余热的效率；ηRFC为热回收装置回收氢燃料电池余热的效率；WRmax为热回收装置一日内回收热量上限。

9）电热装置模型

电热装置出力约束可表示为:

式中:ηp为电热装置的转换效率；WEmax为电热装置一日内回收热量上限。

1.2 短周期功率平衡模型

本文建立了日前-实时协同调度的短周期功率平衡模型。日前调度模型分为两阶段:第1 阶段基于可再生能源与负荷日前24 h 预测数据,在长周期能量平衡模型给出的当日燃油消耗量和储氢量的共同约束下最小化功率调度成本,确定多能微网的日前运行策略；第2 阶段考虑日内可再生能源与负荷不确定性,调动长短周期混合储能备用资源来保障系统的正常运行。通过日前两阶段模型迭代优化可以保证不确定集内任意场景下多能微网运行的鲁棒性。在实时运行时,系统根据新能源的实际出力,结合日前调度策略预留的长短周期混合储能备用资源,得到微网系统实际功率调度策略。

1.2.1 短周期功率平衡第1 阶段模型

1）目标函数

式中:J为短周期功率平衡模型调度时长；COj为第t日j时刻燃油成本；CGj为j时刻机组启停成本；CTjS为j时刻储能装置储能成本；CLj为j时刻系统弃风和弃光成本；CGEj、CP2Hj、CFCj分别为j时刻传统发电机、P2H 装置和氢燃料电池启停成本；CESj、CHSj、CQSj分别为j时刻电、氢、热储能装置的储能成本。

2）功率平衡约束

对于短周期功率平衡模型日前阶段,功率平衡约束可表示如下:

式中:PGEj为j时刻传统发电机功率；PPVj和PPWj分别为j时刻光伏和风电实际发电功率；PFCj为j时刻氢燃料电池发电功率；Pdisj和Pchj分别为j时刻电储能装置放电与充电功率；PP2Hj为j时刻P2H 装置耗电功率；PQj为j时刻电热装置耗电功率；PLj为j时 刻 电 负荷功率；MP2Hj为j时刻P2H 装置产氢速率；Mdisj和Mchj分别为j时刻氢储能装置放氢与充氢速率；MFCj为j时刻氢燃料电池耗氢速率；MLj为j时刻氢负荷速率；QRj为j时刻热回收装置产热功率；QPj为j时 刻 电热装置产热功率；Qdisj和Qchj分别为j时刻热储能装置取热与储热功率；QLj为j时刻热负荷功率。

3）传统发电机补充约束

由于长周期预测的不确定性,本文使用一定比例系数对长周期能量平衡模型给出的当日燃油消耗量约束进行松弛:

式中:λ+GE和λ-GE分别为传统发电机发电量上调和下调松弛系数。

传统发电机启停成本可表示为:

式中:CGEnl为传统发电机组空载成本；CGEsu为传统发电机组启动成本；CGEsd为传统发电机组停机成本；uGEj、vGEj、iGEj分别为表示传统发电机启动状态、传统发电机关闭状态、机组启停状态的0-1 整数变量。

试验所用钼精矿100 g，氧气分压1.20 MPa，固液比1∶10，搅拌转速500 r/min，保温保压时间为300 min，考察不同反应温度对制备样品的影响。

传统发电机启停约束可表示为:

最小启停时间约束可表示为:

式中:XGEon,j-1和XGEoff,j-1分别为传统发电机开机时间和停机时间统计量；TGEon和TGEoff分别为传统发电机需持续开机和停机的最小时间段。

传统发电机爬坡约束可表示为:

式中:ΔPGEmax为传统发电机最大爬坡功率。

4）氢储能装置出力补充约束

由于长周期预测的不确定性,本文使用一定比例系数对氢储能装置出力约束进行松弛。氢储能装置长周期能量平衡调度策略出力约束可表示为:

式中:λ+HS和λ-HS分别为储氢量上调和下调松弛系数。

短周期储能装置包括电化学储能和热储能,两者模型结构相似、形式相同。电化学储能成本可表示为:

式中:CES为储电成本系数；ηCE为电化学储能装置充电效率；ηDE为电化学储能装置放电效率。

电化学储能出力约束可表示为:

式中:EESj为第t日j时刻电化学储能的荷电量；EESmin和EESmax分别为电化学储能装置储电量下限和上限；Pdismax和Pchmax分别为电化学储能装置放电和充电功率上限；uESj为0-1 变量,表示电储能装置的充放电状态,其中,取0 表示放电,取1 表示充电。

与氢储能不同,电储能装置储能周期较短,需满足1 日内能量平衡,即

6）P2H 装置模型

式中:MP2Hmax为P2H 装置最大制氢速率；ΔMP2H为P2H装置最大爬坡速率。

7）氢燃料电池模型

氢燃料电池约束可表示为:

式中:PFCmax为氢燃料电池最大发电功率；ΔPFC为氢燃料电池最大爬坡功率。

除上述约束外,本文建立的多能微网短周期功率平衡调度第1 阶段模型仍需受到传统发电机出力、P2H 装置和氢燃料电池启停状态及热储能装置等约束,但由于与长周期能量调度模型约束或已提及其他设备约束结构相似、形式相同,为避免重复,不再赘述。

1.2.2 不确定集

本文采用基于数据驱动的分布式鲁棒模型刻画新能源出力与负荷的日前预测不确定性。通过历史数据获得K个实际场景,通过场景聚类的方法确定N个离散场景初始概率p0,以场景初始概率为中心,综合考虑1-范数和∞-范数约束条件,得到最恶劣场景分布概率。综合范数约束下可行域ψ为:

式中:ψ1为1-范数约束下的置信空间；p为离散场景分布概率；RN+为正实数集；pn为第n个离散场景分布概率；p0n为第n个离散场景初始概率；ψ∞为∞-范数约束下的置信空间；θ1和θ∞分别为1-范数和∞-范数约束下概率允许的偏差限值。

根据文献［22-24］可知,p满足式（65）和式（66）的置信度。

式中:Pr {∙}为不等式的概率函数。令α1=1-2Nexp(-2Kθ1/Ν),α∞=1-2Nexp(-2Kθ∞),则偏差限值如式（67）所示。

式（67）表明随着历史数据数量N的增加,场景概率分布的估计将更接近真实值,θ1和θ∞会减小直至为0。α1和α∞分别为1-范数和∞-范数约束的置信度,置信度越大,模型考虑的不确定性越大,求解得到的调度策略鲁棒性越强。同时,调度策略也更加保守,导致微网运行的经济性降低。因此,合理的调节这2 个置信度参数,可以实现模型经济性与可靠性的平衡。

1.2.3 短周期功率平衡第2 阶段模型

1）目标函数

式中:CGE为传统发电机成本系数；cES、cHS、cTS分别为电、氢、热储能设备出力调整惩罚系数；cLO为弃电调整惩罚系数；ΔPGEj为j时刻传统发电机出力调整值；ΔPchj和ΔPdisj为j时刻电储能设备出力调整值；ΔMchj和ΔMdisj为j时刻氢储能设备出力调整值；ΔQchj和ΔQdisj为j时刻热储能设备出力调整值；ΔPLOj为j时刻弃电量调整值。

2）功率平衡约束

式中:上标b 表示日前功率调度第2 阶段的对应变量。

3）可再生能源调节约束

式中:PPV,yj和PPW,yj分别为光伏和风电j时刻的出力预测值。

4）传统发电机出力调节约束

式中:PGEmax为传统发电机出力最大值。

5）电储能出力调节约束

式中:Δt为日前功率调度第2 阶段调整单位时间；uE,bj表示日前功率调度第2 阶段电储能装置的储能状态。

6）弃电量调整值约束

式中:PLOj为j时刻的弃电量。

除上述约束外,本文建立的日前功率调度第2阶段模型仍需受到氢储能出力调节和热储能设备出力调节约束,但由于与电储能出力调节约束结构相似、形式相同,为避免重复,本文不再赘述。

需要说明的是,实时运行阶段系统根据可再生能源和负荷实际运行数据,结合日前优化策略预留的长短周期混合储能备用资源,得到微网系统实际调度策略。这一阶段的调度模型与日前调度第2 阶段模型的内层最小化问题相同,为避免重复,本文不再赘述。

2 模型求解

2.1 功率平衡模型迭代求解

多能微网日前功率调度模型为min-max-min 形式的两阶段三层优化模型,现有商用求解器无法直接对其进行求解。本文基于C&CG 算法将多能微网日前功率调度模型分成了主问题（master problem,MP）与子问题（sub-problem,SP）两部分。然而,传统C&CG 算法通常基于强对偶理论将maxmin 形式的双层子问题转化为单层max 形式,求解速度较慢。同时,对于本文所建模型,子问题中包含表征储能充放电状态的二进制变量,无法直接应用强对偶理论,需要采用更为复杂的nested-C&CG 算法［25］,严重影响了模型的求解效率。因此,本文针对分布鲁棒模型的特殊结构,设计了无需对偶转换的C&CG 算法,将max-min 双层问题分解为多个小规模子问题并行求解,提高了模型求解效率。

第s次主子问题迭代中,主问题模型如式（87）至式（89）所示。

式中:X为日前阶段约束条件集合；x为相应决策变量；η为待优化的子问题目标函数值；yn,s为第s次迭代 第n个 场 景 下 子 问题 决 策 变 量；p*n,s为 第s次 迭 代子问题求解出的最恶劣离散场景概率分布；aT和bT为对应目标函数的常数矩阵；A和α为对应约束条件的常数矩阵；S为迭代总次数。

子问题为max-min 两层优化问题,基于给定的主问题决策变量x,针对日内实际运行工况调整调度方案,并寻找最恶劣场景概率分布。第s次迭代中,子问题模型如式（90）所示。

式中:Yn为各场景下子问题变量约束范围集合；yn为第n个场景下子问题决策变量。

由于分布鲁棒模型子问题中子问题的变量约束范围在场景间相互独立,式（90）可以分解为max 和min 两个函数gn和H分步求解,有

通过主子问题之间的迭代,可求解多能微网日前功率调度模型,无须对子问题进行对偶计算,降低了算法的计算复杂度。

实时调度模型为单层线性规划问题,可以使用商用求解器直接求解,快速得到当日实际燃油消耗量和储氢量。

2.2 能量-功率匹配模型滚动求解

如式（1）至式（29）所示,长周期能量平衡模型为单层线性规划问题,可以使用Gurobi 等商用求解器直接求解。其紧凑形式如下:

式中:zt为长周期能量平衡调度阶段决策变量；cT为对应目标函数的常数矩阵；D和d为对应约束条件的常数矩阵。求解式（93）可获得第i次长周期能量调度计划。

多能微网日前功率调度模型的紧凑形式如下:

根据2.1 节所示方法,结合第1 日燃油消耗量和氢储量限制,求解短周期功率平衡日前调度策略。求解实时调度模型,得到第1 日实际燃油消耗量Otruei,1和氢储量Htruei,1如下:

式中:Oj为j时刻的燃油消耗量。

将Oturei,1和Hturei,1返回长周期能量平衡调度模型,更新燃油储存量O0与氢储能装置储氢量H0。

本文建立的计及长短周期混合储能的多能微网长周期能量-功率匹配模型求解流程如附录A 图A3所示。

整体求解步骤如下:

步骤1:设置长周期能量平衡调度次数i=1、燃油初始储存总量O0和氢储能装置初始储氢量H0,获取i至I日新能源发电和负荷预测数据。其中,第i日数据由日前预测模型提供,第i+1 到I日数据由长时间预测模型提供。

步骤2:求解长周期能量平衡模型,得到i至I日能量分配策略,确定第i次长周期能量调度计划第1 日燃油消耗总量Oi,1和储氢量Hdisi,1-Hchi,1。

步骤3:设置短周期功率平衡模型主子问题迭代次数s=0,目标函数上界UB=∞,下界LB=-∞,初始场景概率分布为p0。

步骤4:固定Oi,0和Hchi,0、Hdisi,0,求解式（87）至式（89）主问题,得到主问题最优解（x*s,η*s）,更新下界值LB=max（LB,η*s）。

步骤5:固定x*s,求解式（90）子问题,得到子问题的目标函数值H*s和最恶劣场景的概率分布p*s,更新上界值UB=min（UB,H*s）。

步骤6:收敛性判断。若（UB-LB）/LB小于等于阈值e,则停止迭代,求解实时调度模型,得到Oturei,1和Hturei,1；否则,更新主问题中最恶劣场景概率分布ps+1=p*s,并在主问题中定义新的变量ys+1并添加与新变量相关的约束Ys+1,令s=s+1,返回步骤3。

步骤7:若i=I,停止迭代；否则,令O0=O0-Oturei,1,H0=H0+Hturei,1,i=i+1,返回步骤1。

3 算例分析

本文选取自治运行的电-氢-热耦合多能微网为对象进行算例分析,微网运行能量完全依靠风电、光伏和少量传统发电机提供。系统可再生能源与负荷未来168 h 预测曲线如附录A 图A4 所示。本文基于MATLAB 平台调用Gurobi 求解器对模型进行求解。计算机CPU 为AMD Ryzen 5 2500U（2 GHz）、内存为12 GB。

3.1 不同储能场景下系统优化效果分析

为了验证自治型新能源微网长周期调度时氢储能的优势,本节设定了2 种不同储能场景进行对比验证。

场景1:电-氢-热耦合多能微网中,仅采用短时间尺度电储能、热储能。

场景2:电-氢-热耦合多能微网中,采用短时间尺度电储能、热储能,配合长时间尺度氢储能装置。

除储能方式外,2 种场景其他因素完全相同。分布鲁棒优化算法参数为:α1=0.8,α∞=0.8,N=1 000,K=10。

3.1.1 不同储能场景下系统运行稳定性分析

2 种场景下不同储能方式168 h 的充放状态分别如图1（a）和（b）所示。由图1 可知,电储能与热储能总是在24 h 内重复充放,以平衡可再生能源日内出力不平衡。氢储能于前4 日将富余可再生能源转换为氢气进行存储,后3 日供给负荷,对可再生能源长周期出力进行平衡。对比结果验证了氢储能装置平抑长周期可再生能源出力波动的效果。

图1 不同储能场景下调度策略储能数据对比Fig.1 Comparison of energy storage data of scheduling strategies in different energy storage scenarios

2 种储能场景下系统1 周功率平衡调度结果如图2 所示。图中:PD 为电储能装置充放电量；PW 为风电发电量；PV 为光伏发电量；PG 为传统发电机发电量；LD 为电负荷；FC 为燃料电池发电量。对比图2（a）和（b）的系统平衡数据图可以看出,相比于场景1 前期大比例弃电、后期依靠传统发电机补足的情况,场景2 基本完全消纳了调度周期内可再生能源,降低了微网对传统发电机的依赖度,提升了微网调度策略的可靠性。

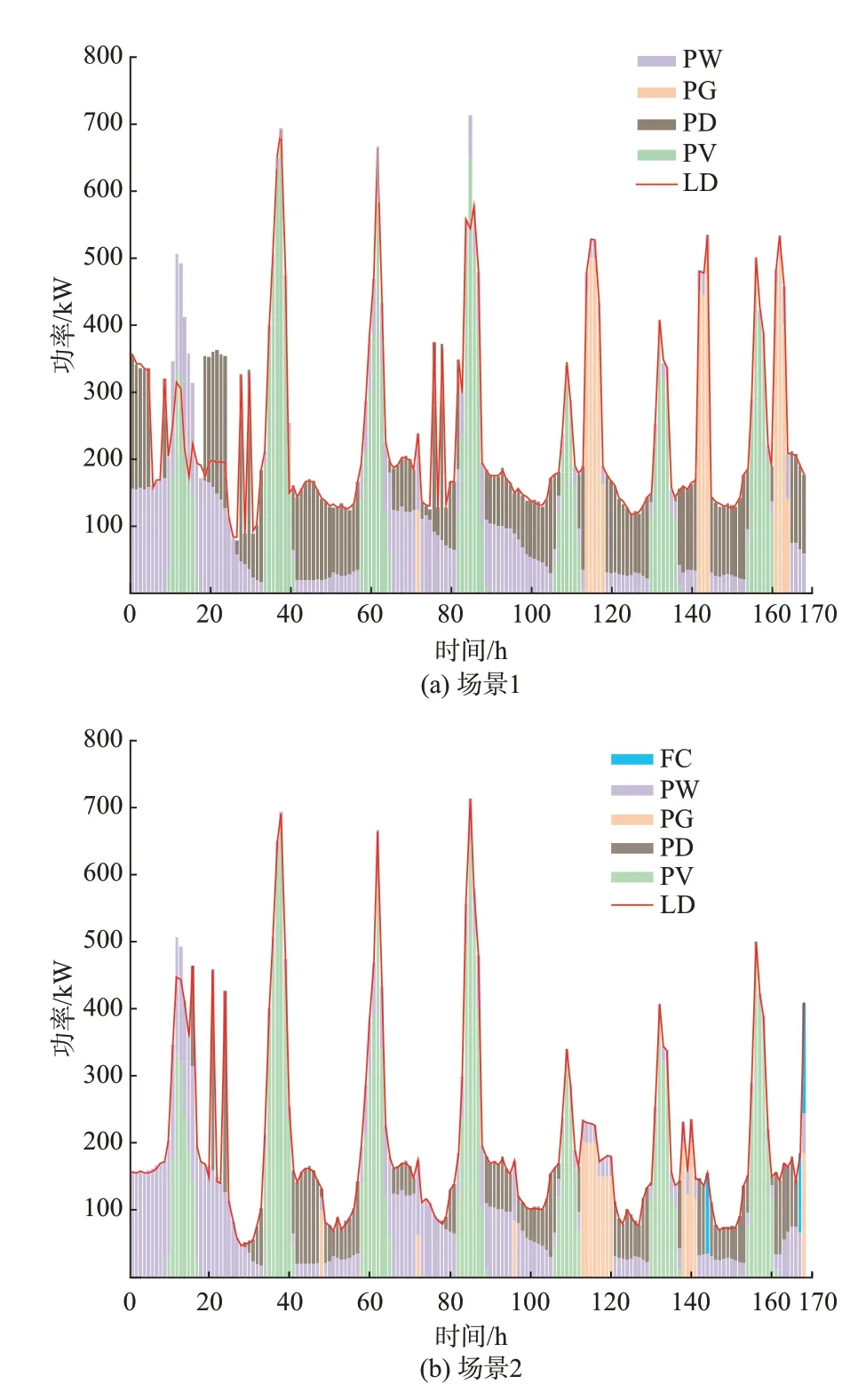
图2 不同储能场景下调度策略平衡数据对比Fig.2 Comparison of balancing data of scheduling strategies in different energy storage scenarios

3.1.2 不同储能场景下系统运行经济性分析

图3 展示了2 种场景下系统的调度成本。可以看出,在同种情况下,场景2 的调度成本远远低于场景1。这是因为调度周期的第1 日,风电与光伏提供的能量远大于负荷的需求,场景2 将富余的电能转化为氢气进行存储,而场景1 进行弃光、弃风产生了大量的惩罚成本。针对调度周期后3 日风电与光伏出力不足的情况,场景1 只能使用传统发电机进行出力补偿,而场景2 使用了前期储存的氢气发电进行补偿,节省了传统发电机出力消耗的燃油成本。2 种场景的对比验证了长短周期混合储能的方式能够提高可再生能源微网系统的运行经济性。

图3 不同储能场景下调度策略经济性对比Fig.3 Economic comparison of scheduling strategies in different energy storage scenarios

3.2 功率-能量匹配调度模型可靠性分析

为了验证长周期多能微网能量-功率匹配调度可靠性,本节设置传统连续日前调度模型进行对比分析,选取分布鲁棒优化算法的参数为:α1=0.8,α∞=0.8,N=1 000,K=10。

传统连续日前调度模型调度结果如图4 所示。由图4 可知,在调度周期前期,由于可再生能源充足,传统连续日前调度模型能够维持系统稳定运行；调度周期后期,可再生能源出力不足,传统连续日前调度模型基于日前24 h 可再生能源与负荷预测数据进行调度,不考虑长周期系统稳定性,导致大量储氢转化为电力消耗,系统后期能源供给不足,产生失负荷现象。对比图2（b）可以明显看出,功率-能量匹配模型能够协调长周期调度方案与短周期调度方案,提高了多能微网系统长周期调度策略的可靠性。

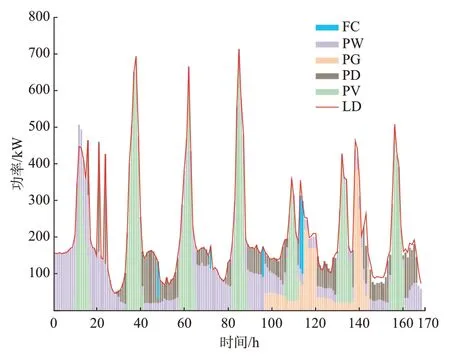
图4 传统连续日前调度策略平衡数据Fig.4 Balancing data of traditional continuous day-ahead scheduling strategy

3.3 数据驱动的分布鲁棒优化结果及相关对比分析

3.3.1 不同范数约束下结果对比分析

为了验证综合范数约束的全面性,本节设置了单独范数约束场景与综合范数约束场景进行对比分析,选取分布鲁棒优化算法的参数为:N=1 000,K=10。

选取α∞=0.8,α1=0.5、0.8、0.99,计算结果如表1 所示。由表可知,对于综合范数约束而言,随着α1的增加,系统运行成本相应增加,符合式（65）、式（66）约束。对比综合范数约束与单独∞-范数约束下系统计算结果可知,由于综合范数受∞-范数约束的同时,考虑了1-范数约束条件,系统运行成本较单独∞-范数约束更低,保守性更低。

表1 综合范数与∞-范数系统运行成本对比Table 1 Comparison of system operation costs between comprehensive norm and ∞-norm

选取α1=0.8,α∞=0.5、0.8、0.99,计算结果如表2 所示。同上,由于综合范数受1-范数约束的同时,考虑了∞-范数约束条件,系统运行成本较单独1-范数约束更低,保守性更低。

表2 综合范数与1-范数系统运行成本对比Table 2 Comparison of system operation costs between comprehensive norm and 1-norm

3.3.2 不同不确定性方法结果对比分析

为了验证本文所使用分布鲁棒优化算法的经济性和高效率,本节在2.2 节提出的场景2 下,将本文使用的数据驱动的分布鲁棒优化结果与文献［22］对偶求解的分布鲁棒优化、传统鲁棒优化结果进行对比分析。其中,数据驱动的分布鲁棒优化算法和对偶求解的分布鲁棒优化算法的参数选取为:α1=0.8,α∞=0.8,N=1 000,K=10,鲁棒优化算法波动范围为预测值的20%。

3 种优化算法下系统的计算结果如图5 所示。由图5 可知,求解多能微网调度模型时,数据驱动的分布鲁棒优化算法与对偶求解的分布鲁棒优化成本相差无几,而传统鲁棒优化成本则明显高于其他两者。说明相对于鲁棒优化算法只考虑最恶劣场景信息,分布鲁棒优化算法在保证鲁棒性的基础上更具有经济性。

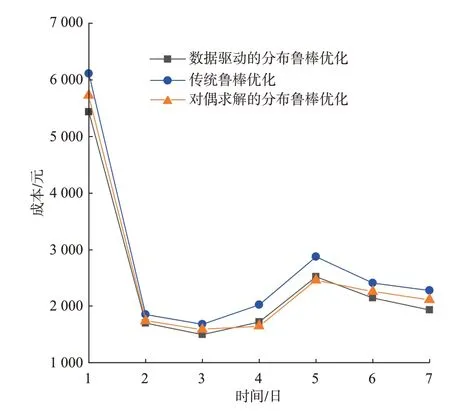
图5 不同不确定性方法经济性对比Fig.5 Comparison of economy of different uncertainty methods

同种场景下,3 种不确定性方法求解速度对比结果如表3 所示。可以看出,相比于传统鲁棒优化模型,数据驱动的分布鲁棒优化模型和对偶求解的分布鲁棒优化模型迭代次数更少。这是因为分布鲁棒模型使用范数对离散场景概率分布进行约束,收敛效果更好。相比于传统鲁棒优化模型和对偶求解的分布鲁棒优化模型,数据驱动的分布鲁棒优化模型求解速度显著提高,能够满足系统日前调度计算的需要。这是因为与对偶求解的分布鲁棒模型和传统鲁棒模型将max-min 问题对偶求解不同,数据驱动的分布鲁棒优化模型第2 阶段问题可行域与不确定集不相交,在求解时,可以将SP 问题分解成多个SP 问题并行求解,大大提高了模型的求解速度。同时,以系统第1 日日前调度为例,4 次迭代求解中,第2阶段模型求解时间分别为2.313 8、2.454 9、2.268 9、2.125 6 s。实时调度模型与日前调度第2 阶段模型的内层最小化问题相同,求解时间同为秒级,能够满足系统实时计算时间要求。

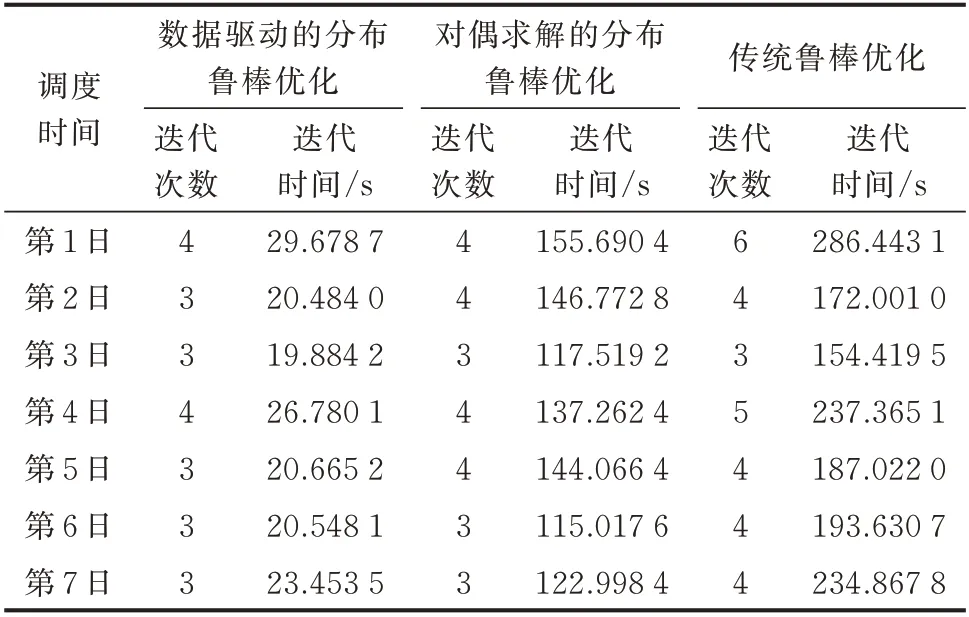
表3 不同不确定性方法求解效率对比Table 3 Comparison of solution efficiency of different uncertainty methods

4 结语

本文提出了一种计及长短周期混合储能的多能微网能量-功率匹配滚动优化方法,并采用分布鲁棒优化算法对可再生能源与负荷的时空不确定性进行建模,提升了微网的自治运行能力。结合算例分析,可得如下结论:

1）长短周期混合储能的协同应用可以有效提升系统运行的灵活性,增强可再生能源的消纳能力,降低传统发电机的燃油消耗量,提高系统运行的整体经济性；

2）通过长周期能量平衡与短周期功率平衡滚动优化,降低了可再生能源与负荷长周期预测误差对调度结果的影响,增强了多能微网长期自治运行的可靠性；

3）采用基于数据驱动的分布鲁棒优化算法,综合1-范数和∞-范数对源荷不确定性离散场景概率分布波动范围进行约束,在保障多能微网运行鲁棒性的同时避免了运行方案的保守性。与传统鲁棒优化算法相比,分布鲁棒优化算法求解过程更简单、结果更经济。

在未来的研究工作中,将进一步探索多个多能微网间的协同互济。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。