膨胀土变形特性和基于Mohr-coulomb准则本构关系

聂去尘, 庄心善, 周 荣, 文 武

(湖北工业大学土木建筑与环境学院, 湖北 武汉430068)

膨胀土是一种强度较高且塑性较好的特殊黏土[1],在外力作用下其变形性状较为复杂,需通过室内外试验来研究它的变形和力学特性,如膨胀土剪胀性和压硬性的耦合关系,剪胀角的取值,以及本构模型的选择等问题,这可为膨胀土工程设计的科学性、合理性、安全性提供重要的理论支撑。

国内外学者对此已有相关研究,并取得了大量的科研成果。王靖涛[2.3]等系统阐述了土体材料体应变与剪应变的交叉关系,得出主应力差和静水压力同时作用于体积变形和剪切变形。罗刚等[4]通过研究Duncan-Chang双曲线增量模型以及双屈服面模型,并结合两者优势综合反映了土的应变软化和应变硬化特征。Rowe等[5]以砂土土体为例,在考虑了临界状态、孔隙比后修正了应力剪胀理论,进而得出剪胀角的概念。李朝阳[6]等依据膨胀土的亲水性特点,深度研究含水率与膨胀土各强度指标之间的关系,提出了基于Mohr-Coulomb准则的本构模型。

综上所述,学者们在岩土体材料应变耦合作用和本构关系[7]方面已有成熟的科研成果,本文首先针对膨胀土这一特殊黏土,对土体材料的压硬性和剪缩性的耦合现象进行理论上的适用性验证。由于目前许多本构关系的建模思路来自Cam-Clay模型,而Cam-Clay模型构造思路源于塑性关联流动,导致剪胀角大于实际值,意味着在剪切破坏过程中土体会严重压缩或膨胀。而依据应力剪胀理论推导的剪胀角定义[8]又来自于砂土等土体材料的试验依据,对于膨胀土这一特殊黏土并不适用。本文通过分析固结排水试验数据,以膨胀土的剪切应变与体应变的关系获得更精确的剪胀角值,进而研究膨胀土的广义塑性本构关系。

1 膨胀土室内试验

本文试验取用的膨胀土来自安徽某处高速公路工程,其相关指标见表1。

表1 膨胀土基本物理力学性能参数

1.1 试验方案

1.1.1侧限压缩试验该试验只对膨胀土施加竖向荷载并保证无侧向形变,需在固结仪内完成,如图1a所示。

图1 试验仪器

试验时,将饱和后的膨胀土放入固结仪内,并施加竖向荷载,依次加载至25 kPa、50 kPa、100 kPa、200 kPa、300 kPa、400 kPa、800 kPa、1600 kPa等,要求保证各级加载结束时的竖向位移下降值不超过0.01 mm/h。

1.1.2常规三轴试验固结排水试验三轴仪如图1b所示,由于剪切试验过程中不能出现超孔隙水压力,故应当控制剪切速率为0.006 mm/min。

试验时将饱和度B检测值不小于0.95的膨胀土土样放入应变式全自动三轴仪器内,随后使试样分别在100 kPa、200 kPa、300 kPa的围压下充分排水固结,而后对土样施加附加轴向压力,且围压为定值,直至膨胀土被剪切破坏。

2 试验结果与分析

2.1 侧限固结试验

该试验以e-lgP曲线描述膨胀土的压缩性能,由图2可知,当竖向荷载加至300 kPa时,e-lgP关系逐渐趋于线性,其斜率的绝对值即为压缩指标CC。由表2可得压缩指数均小于0.3,是压缩性较低的土,表明刚度较高。此外,该膨胀土所施加的荷载越高,则压缩模量Es也就越大,表征膨胀土具有很强的压硬性。

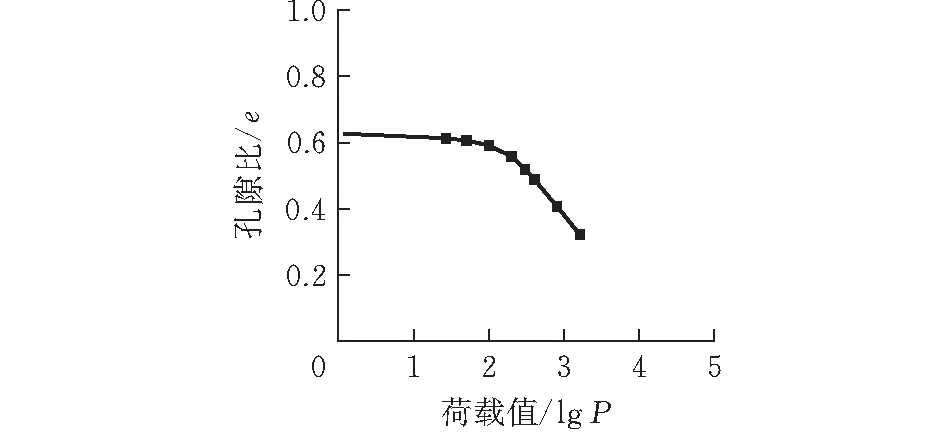
图2 膨胀土e-lgP关系

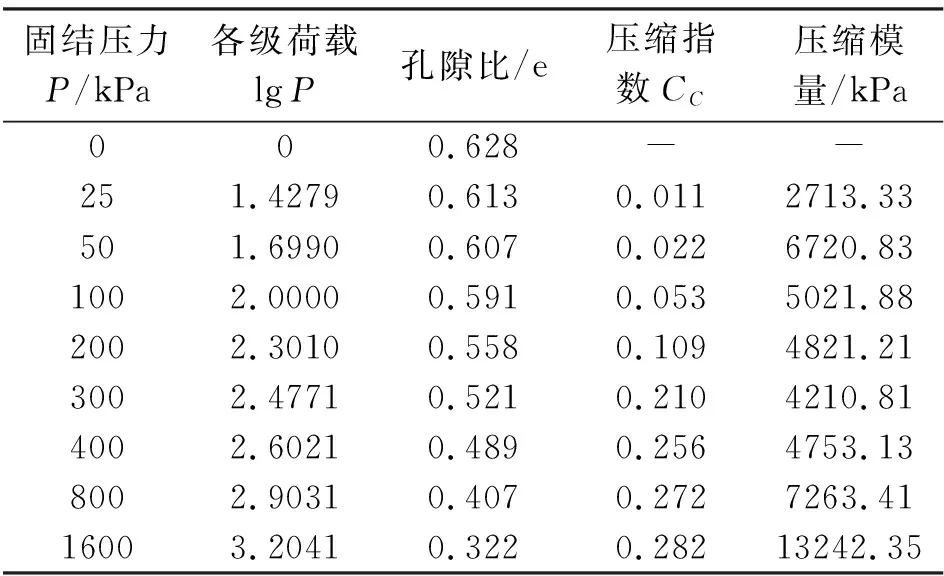
表2 固结试验结果

2.2 三轴固结排水试验

2.2.1压硬性如图3所示,发现当膨胀土轴向应变增加到约10%时,剪应力σ1-σ3增势由陡峭渐趋于平缓,最终进入持续的应变状态;且在这一持续的应变状态下,膨胀土所承受的围压越高则剪应力越大,且不同围压下剪应力破坏峰值增幅明显,表明膨胀土的强度随围压的增大有明显的提高,膨胀土的变形具有类似双曲线轨迹的硬化特征。这是由于外部压力压缩了膨胀土内部的孔隙空间,从而导致土粒与土粒之间的接触面积增大、咬合力更强,从而使得抗剪能力更高。

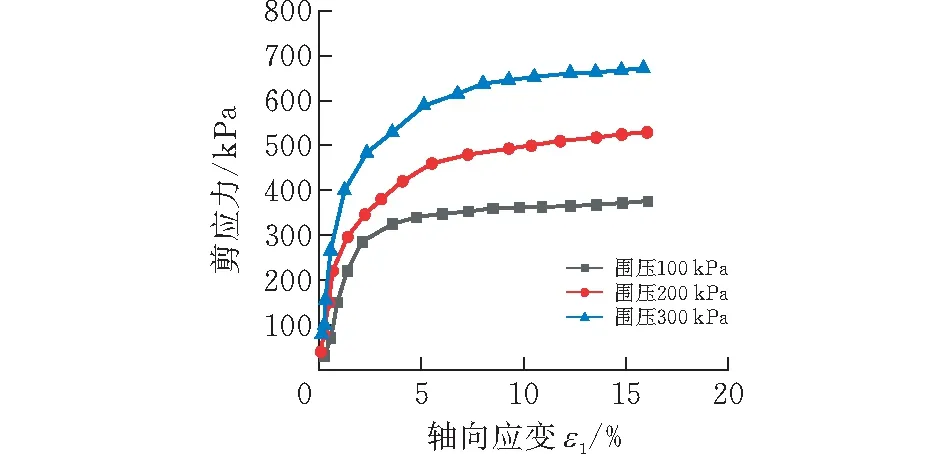
图3 应力-应变曲线

2.2.2剪缩性由于固结排水剪切过程中,膨胀土还产生了体积减小的形变,由图4可知,当体应变达到约1%时剪应力增量基本呈线性,当应变超过1%时,剪应力的增量逐渐趋于平缓,这是因为土颗粒间受外力作用使其排列更加紧密,压缩了颗粒间的孔隙空间,从而发生了体积减小的形变,也就是膨胀土剪缩性的体现。

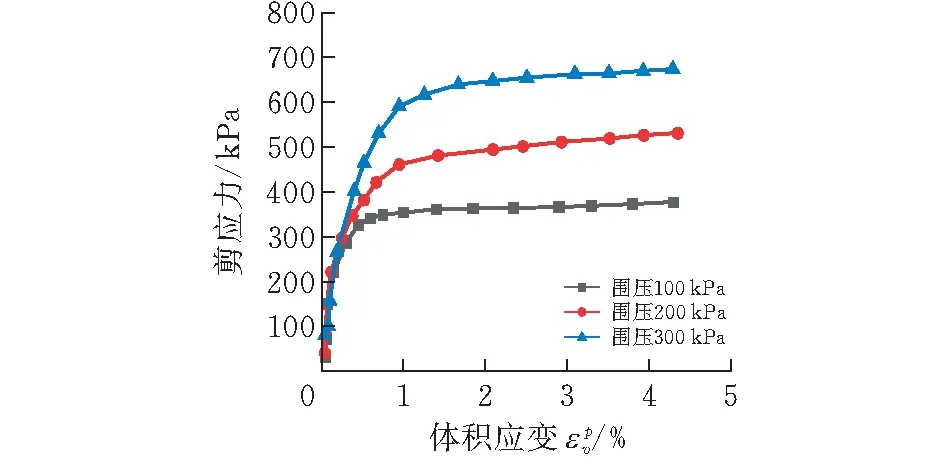
图4 膨胀土的主应力差-体积应变曲线

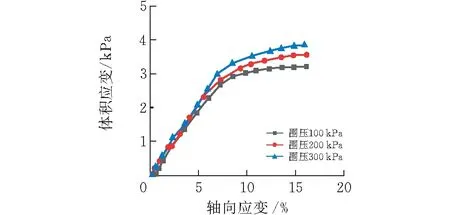
图5 膨胀土的体变-轴向应变曲线

由图6可知,轴向应变与体积压缩应变呈正相关,当轴向应变达到约8%时,体积应变减缓;当轴向应变已达到破坏应变时,体积应变几乎维持恒定,接近峰值。

2.3 膨胀土压硬性与剪缩性的耦合

在固体变形中,应力的产生和传递是通过物体的变形实现的,从这一概念出发,在正常固结剪切阶段,饱和膨胀土的剪缩效应使得土体受到压缩,其压硬效应使得土体难以被剪切以致破坏,而后者的效应正是由于膨胀土的体积被压缩所致,即可以理解为膨胀土体积的压缩延缓了其受剪破坏趋势,应力应变关系如本文图2、3、4、5所示,呈双曲线函数关系,如本文的固结排水试验所表现的高围压下正常固结排水膨胀土的应变硬化现象。由此可以看出,膨胀土压硬性与剪缩性的耦合关系存在对彼此作用方式上的区别,剪应变通过剪缩直接影响体应变,体应变要通过改变抗剪能力间接影响剪应变;抗剪能力的改变都是来自于塑性体应变的作用,即塑性体应变的变化控制着抗剪能力的升降。如图6所示,清楚地表达了两者相互作用的方式即耦合关系。

3 本构关系的修正

3.1 膨胀土剪胀角的选取

剪胀角是表征土体材料塑性应变与剪切应变之间夹角的量值,采用符号ψ描述,它反映了土体材料所受剪切应力与体积应力的耦合关系。若剪胀角与内摩擦角取值相同,便假定了广义塑性力学中的屈服面与塑性势面重合,即遵循关联流动法则,从而放大了土体的剪胀作用;若剪胀角取值偏高意味着在剪切破坏时会发生超出实际工程情况的体积膨胀现象[9]。若忽略剪胀角,假定土体在受剪破坏过程中无体积变化,又违背工程设计的实际需求。于是在大量的平面应变工程选取剪胀角的问题中,许多学者通常取值为内摩擦角的1/2,简便易得,但准确度不高。

为此,本文拟采用以下公式,结合试验数据得出较为精确的剪胀角值,公式[10]如下:

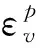
3.2 Mohr-Coulomb屈服条件

假定膨胀土为各向同性体,且三个主应力均已通过试验确定,由Mohr-Coulomb屈服准则的塑性本构理论[11]可得以下推导过程,首先屈服准则可表示为:

(1)

式中σ1,σ3取自三轴试验中的轴压值和围压值。

屈服条件式(1)还可以表示为:

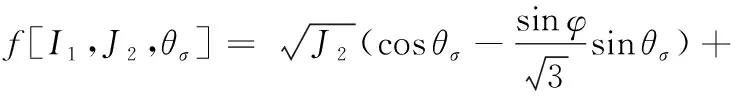
(2)

式中I1是第一主应力不变量,J2是应力偏量第二不变量,θσ是Lode角。

复合求导后,得塑性应变增量为:

(3)

式中:

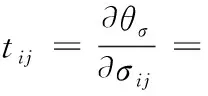
(4)

屈服函数F对应力张量σij的偏导数运算,可得:

(5)

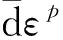
将式(4)代入式(5)可得:

(6)

式(6)括号中的的第一项反映塑性体积应变增量,后面二项反映塑性偏应变增量,其中各系数β1、β2、β3分别为:

(7)

依据非关联流动法则,将以上屈服函数F式中的内摩擦角φ值替换为剪胀角ψ值。

使用式(5),并利用式(7),则有

(8)

进而得:

(9)

3.3 Mohr-Coulomb本构关系的验证与预测

由试验结果可整理得到累积塑性应变和体积应变的关系如图7所示,当体积应变超过1%时,膨胀土的累积塑性应变与体积应变的增长趋势基本呈线性关系,这一现象验证了式(9)中推导的累积塑性应变增量与体积应变增量的比值呈与剪胀角值相关的线性变化趋势、且该比值基本保持恒定这一结论。

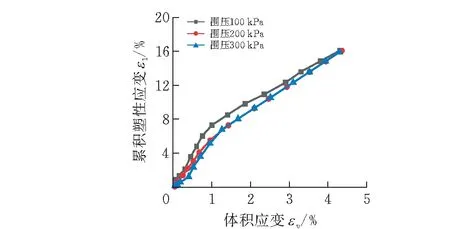
图7 累积塑性应变-体积应变曲线

并且进一步由图7可拟合得出这两个变量的斜率,即累积塑性应变与塑性体积应变的微分关系,如图8所示,为不同围压下膨胀土的累积塑性应变与体积应变的曲线关系与其拟合曲线图的对照,可知在围压分别为100 kPa、200 kPa、300 kPa时,随着塑性体积应变的增加,累积塑性应变基本呈线性增长,并得出拟合公式:

图8 围压300 kPa的累积塑性应变-体积应变关系

Y1=3.644×X1+1.736

(10)

Y1=3.782×X2+0.822

(11)

Y1=3.187×X3+0.545

(12)

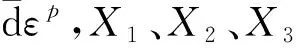
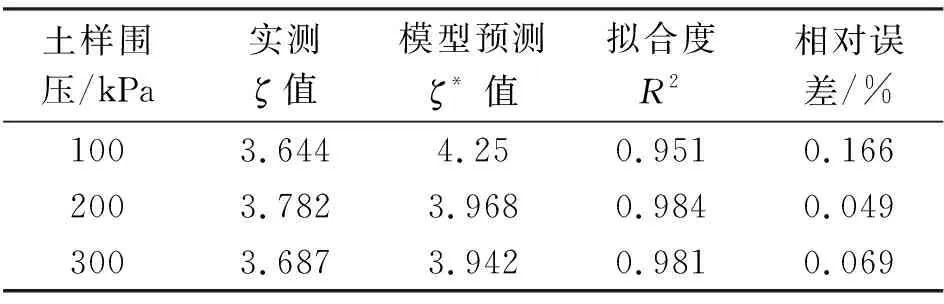
表3 累积塑性应变增量与体积应变增量比值系数ζ

4 结论

1)通过侧限固结试验、常规三轴压缩试验分别验证证了膨胀土压硬性与剪缩性的耦合关系,并且得出第一一主应力形变是体应变的约4倍,其形变均呈现应变硬化特性,由于未能把应变软化包括进来,因此还不能很好描述当膨胀土出现强度峰值以后的变形特性。

2)本文对剪胀角的定义给出的基于固结排水试验结果相关的塑性体积应变与轴向应变的数学公式可较精确地定义剪胀角,从而进一步提高膨胀土剪应力与静水压力的耦合关联度。

3)证明了Mohr-Coulomb本构模型对研究膨胀土的变形特性具有很强的适用性,非关联流动法则的实现也较为方便,本文只将内摩擦角φ值替换成剪胀角ψ,从而修正了膨胀土的本构关系,且参数易测,这一模型特别有利于测定土体变形指标后针对平面应变问题的工程计算。