基于GA优化的模糊PID控制螺旋给料计量系统

谢 鑫, 徐 巍, 朱怀志, 成家宝

(湖北工业大学机械工程学院, 湖北 武汉 430068)

螺旋给料计量系统由于其价格低廉、输送稳定、使用寿命长等特点被广泛应用于定量包装与称重配料行业[1]。由于在螺旋给料计量控制系统中,螺杆的转速与粉末流量之间为非线性关系,在实际工作时常出现计量精度低、流量稳定性差等问题。这些问题不仅会直接影响加工出成品的质量,也容易造成原料的浪费。因此,如何提高螺旋给料计量系统流量的稳定性,是进行螺旋给料计量系统设计时需要关注的重点,也是企业改善生产问题、提高生产效率的一个重要方向。当前,国内最常使用的传统PID控制虽能满足基本控制需求,但不能实时调整参数,容易受到外部扰动以及内部参数变化的影响,难以保证系统的精度与鲁棒性[2]。近年来,智能控制理论为改善定量螺旋给料计量系统的给料速度和出料精度提供了新的途径。彭博等[3]和王江华等[4]将模糊控制与PID控制结合并应用在定量给料包装系统中,相比与传统PID控制提高了性能,但仍存在上升速度慢的缺点;杨晓等[5]将短反馈理论与模糊PID控制结合,提出了基于模糊短反馈PID控制的计量控制系统,并应用到螺旋给料包装机中,解决了给料速度慢与精度低的问题,但抗干扰能力并未明显改善。李丽等[6]将Ziegler-Nichols算法与PI控制算法结合,可实现比例和积分系数的在线调整,提高了计量系统的收敛速度和跟踪能力,但仍存在抗干扰能力较差的问题。李雪梅等[7]提出通过神经网络优化PID参数的方法,借助神经网络的自学习能力对PID参数自整定,进而提高粉末计量系统的流量稳定性,但神经网络训练时间长,不适用于实际生产。相比于上述控制算法,本文借助遗传算法优化模糊PID控制器参数的算法,具有响应速度更快、可对外界环境迅速做出反应的优点,能够有效提高定量螺旋给料计量系统的响应速度与抗干扰能力。

1 螺旋给料控制系统

1.1 定量螺旋给料结构

定量螺旋给料结构(图1)[4]主要由进料仓、伺服电机、称量传感器、螺杆等结构组成。其中:伺服电机用来提供动力控制螺杆旋转的转速和旋转圈数;螺杆是螺旋给料结构的核心组件,由心轴和螺旋叶片组成。

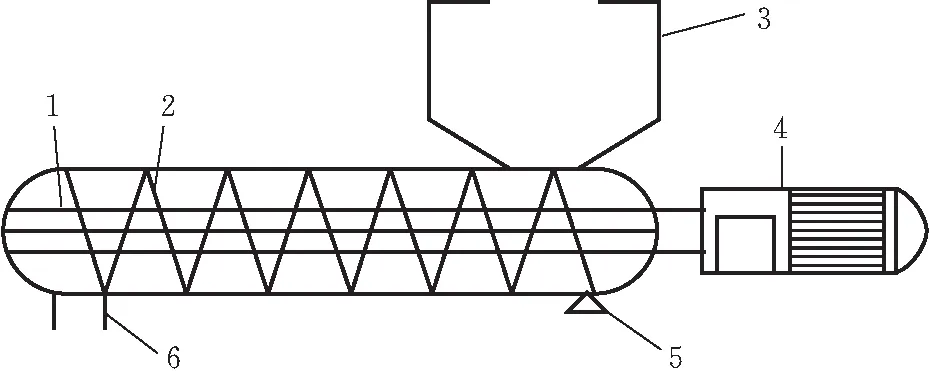
1-心轴; 2-螺旋叶片; 3-料仓; 4-伺服电机;5-称重传感器; 6-出料口

1.2 控制系统工作流程

系统控制流程由图2所示。首先需预先设定好目标值,工作时,物料的质量通过质量传感器传递到控制器,控制器根据实际值与目标值的差值实时调整发送给伺服电机的信号,电机接收到信号后精准调整螺杆的转速和总旋转圈数进行下料。在当前值与目标值差距过大时,快速给料,在接近设定的阈值时,缓慢下料,当达到物料的质量等预先设置的目标值时,停止给料,完成给料操作。

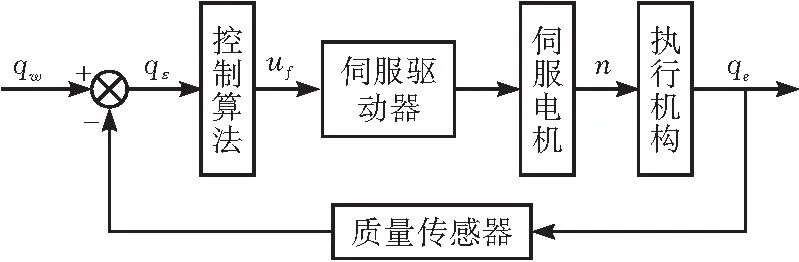
图2 控制流程

2 螺旋给料系统数学模型

通过图2可知,控制系统的数学模型由信号传递模型、电机模型与螺旋给料机构模型组成。其中,控制信号的传递模型可简化为基本比例环节。

文献[6]给出了螺旋包装机结构理论流量公式

Q(t)=15π(D2-d2)npφSC

式中:Q为螺旋给料流量;D为螺旋叶片直径;d为转动轴直径;n为螺旋轴的转速;p为螺距;φ为螺旋轴转速;S为螺距;C为倾角系数。

令k=15π(D2-d2)pφSC。由于电机转速与角速度成正比例关系,令kc=2π。得

n=kcω

联立可得

Q=kkcω

(1)

假设伺服电机转轴的惯量为J,电磁转矩为M,伺服电机的力矩方程为:

(2)

其中,fa为伺服电机的阻尼转矩系数,ML为电机的负载转矩。伺服电机电磁转矩的表达方程式为:

M=CTφΙcosφ=kTIa

(3)

式中:kT为伺服电机的等效转矩系数,Ia为负载电流。不考虑伺服电机的负载转矩ML。由式(1)和式(2)可得

(4)

伺服电机产生的反电势

(5)

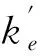
(6)

联立式(4)、(5)和(6)可得

式中:La为伺服电机的线间电感系数,Ra为线间电阻系数。带入式(1)并经Laplace变换可得

其中:U表示计量系统输入(电压),Q表示计量系统输出(给料流量)。则计量系统传递函数方程式为

化简后

3 系统控制方法

3.1 PID控制算法

传统PID控制器是一种反馈控制器,通过不断地比较实际值与目标值,逐渐消除之间的差距,直到实际值等于目标值[8]。实际应用中,PID控制器结构简单,调节参数不依赖系统的具体模型,只需选择合适的PID控制参数即可满足大部分控制需要,因此被广泛应用在各行各业中,其控制原理如图3所示。

图3 PID控制器

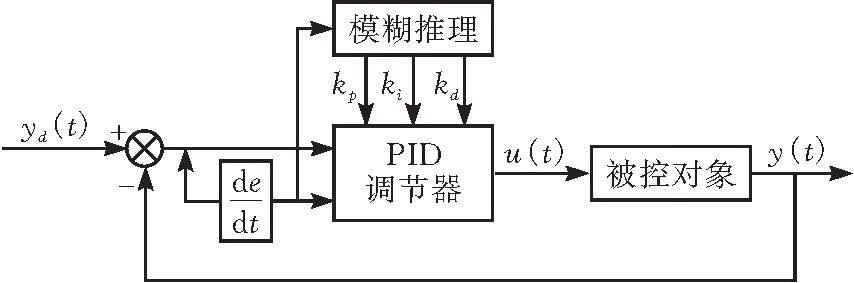
图4 模糊PID控制器

控制系统的输入输出之间的关系可表示为:

e(t)=yd(t)-y(t)

式中:kp为比例系数;T1为积分系数;TD为微分系数;e(t)为PID控制系统的输入;G(s)为控制系统输出。

3.2 模糊PID控制算法

在传统的PID控制器中,控制器的参数Kp,Ki,Kd都是给定的,一旦实际情况与理想情况出现偏差,PID控制器的性能往往难以达到需求。模糊PID控制器则将模糊数学的基本理论和方法应用于传统PID控制器中,通过模糊集表示规则的条件和操作。模糊PID控制器相比与传统PID控制的优势在于,其能根据系统的响应情况使用模糊推理,实现对PID参数的实时调整。

螺旋给料计量控制系统的模糊控制器设计首先需要确定的是模糊控制器的输入输出语言变量。本系统选择二维模糊控制器整定PID控制器参数,将称量值偏差e和称量值偏差变化率ec作为输入变量,PID控制器参数Kp,Ki,Kd作为输出变量。模糊控制流程如下。

1)确定隶属度函数。隶属度函数表示了论域中元素属于该规则的程度,目前常见的隶属度函数有正态分布形、高斯形、梯形、三角形等。其中:正态分布型与高斯型虽能够更精确的表示元素的隶属度,但难于计算;三角形在精度上略有不足,但计算方便,能够有效节约时间。因此选择三角形的隶属度函数。

2)建立模糊控制规则表。模糊规则是人们根据专家经验或试凑法等的经验总结,是模糊PID控制器调整PID参数的依据。本系统中,控制器根据不同时刻的物料计量的偏差实时修改PID参数。本文使用的模糊规则如表1所示。

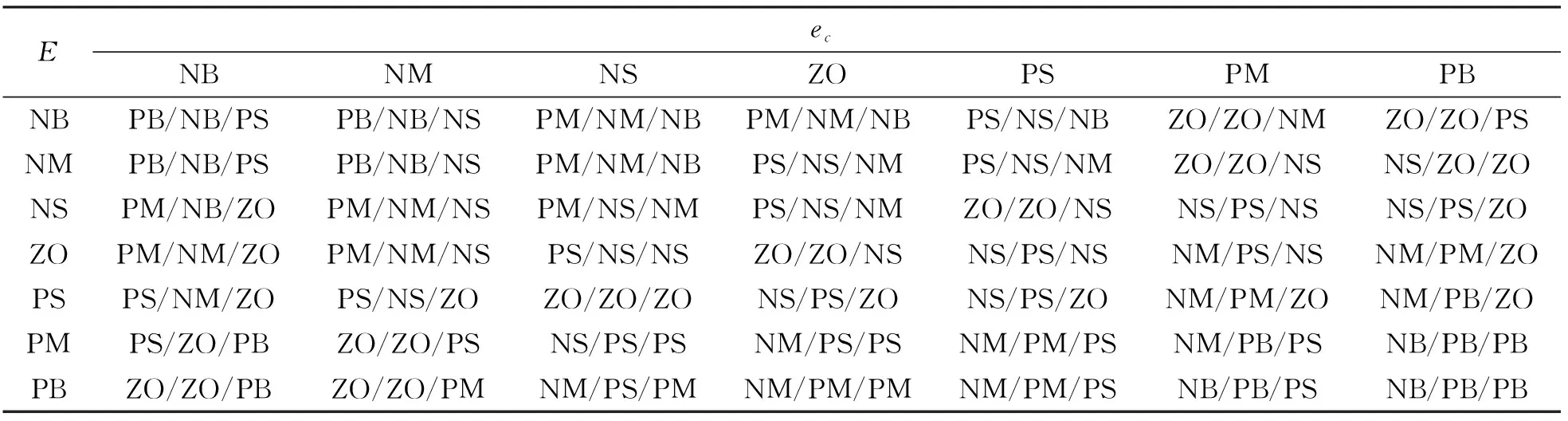
表1 Δkp,Δki,Δkd模糊规则

3.3 基于GA优化的模糊pid控制系统设计

遗传算法(GA)是一种高效的全局搜索方法,具有处理多参数最优化问题的优异能力[9]。通常模糊PID控制规则大部分依靠专家经验法或采用试凑法来进行制定,这使得控制系统在运行时具有一定的灵活性,但却难以在外部环境迅速变化时保证精度。因此本文借助遗传算法对模糊控制器的模糊规则进行在线迭代,求解出最优模糊规则,进而获取优异的控制性能。基于遗传算法优化的模糊PID控制器如图5所示。

图5 基于遗传算法优化的模糊PID控制器

遗传算法的控制流程如下。

1)染色体编码 通过二进制码字符串对模糊控制的参数[e,ec,Kkp,Kki,Kkd]进行编码,即需要将用来描述参数的模糊规则值{NB,NM,NS,ZO,PS,PM,PB}依次编码,从而将模糊控制规则表转换成二位矩阵,再根据二维矩阵生成染色体个体。

2)适应度函数标定 适应度函数是遗传算法中用来评价遗传算法控制性能的标准,合适的适应度函数能有效提高算法的收敛速度。为提高系统响应速度,缩小达到目标的时间,适当降低状态偏差e后构建出的适应度函数F:

式中:ω1、ω2与ω3为权重系数,k为缩放因子。

3)选择 选择指将当前种群中选择适应度较好的个体保留,使其遗传到下一代。本文选择轮盘赌法,将个体被选中的概率与其适应度值结合,适应度越大则被选择的概率就越大。个体被选择的概率

4)交叉、变异 杂交概率Pc和变异概率Pm决定着种群的收敛速度和多样性。基于遗传算法,个体之间按照固定交叉概率Pc交换染色体的部分基因和固定变异概率Pm对部分基因位进行变异操作,从而得到新的染色体。为了提高种群的多样性,Pc应取较大值,Pm应取较小值;为了提高种群的收敛速度,Pc应取较小值,Pm应取较大值。因此为了提高种群的收敛速度,本文使用可变杂交与变异概率:

杂交概率范围:

[Pc1,Pc2]

变异概率范围:

[Pm1,Pm2]

遗传算法流程如图6所示。

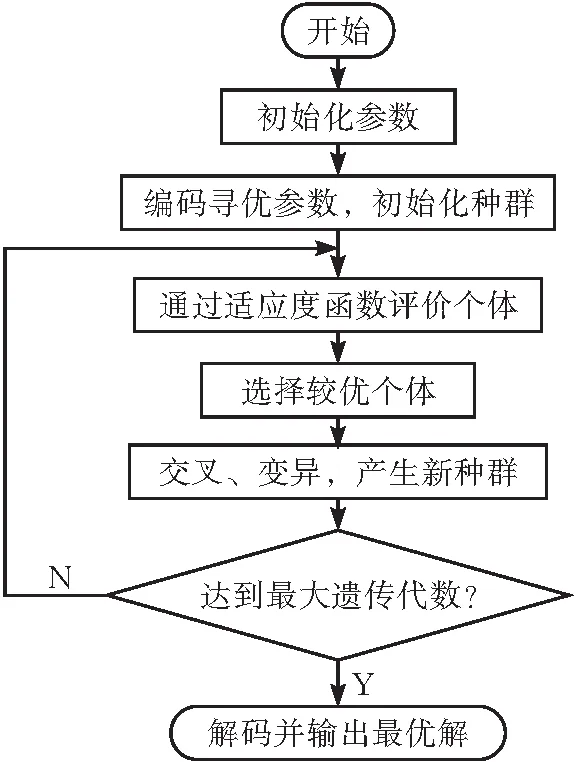
图6 遗传算法流程

4 仿真分析

在Matlab/Simulink环境下,先建立基于遗传算法优化的模糊PID(GA-Fuzzy-PID)控制器系统模型,再将螺旋给料系统数学模型与GA-Fuzzy-PID控制器模型结合,得到的螺旋给料计量系统控制模型如图7所示。与传统PID控制和模糊PID控制方法进行比较,仿真结果如图8所示。

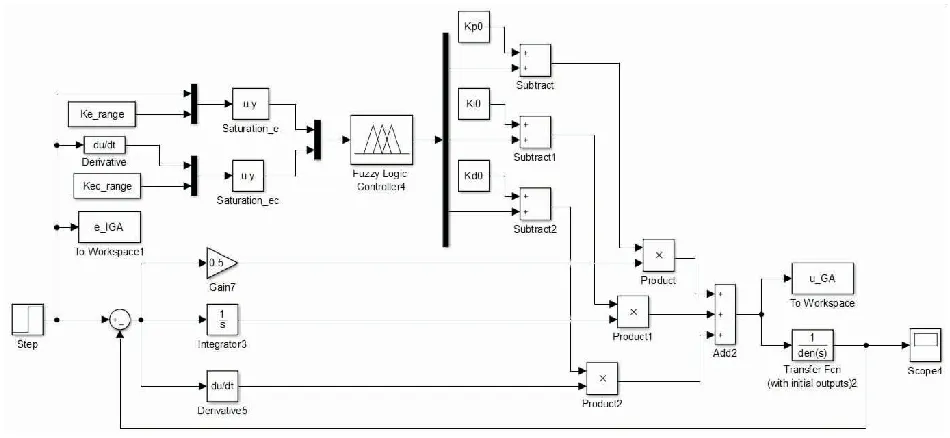
图7 螺旋给料计量系统控制模型

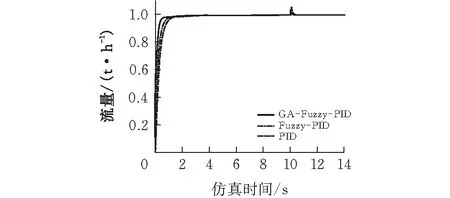
图8 不同算法下的阶跃响应曲线

由图8可看出,GA-Fuzzy-PID控制器能够根据不同的控制要求自适应调整控制器的参数,上升速度更快。在10 s加入幅值为0.2的干扰信号后,改进后的GA-Fuzzy-PID控制器在0.329 s恢复稳定,最大扰动幅值为0.034。相比于传统PID与模糊PID控制,GA-Fuzzy-PID控制器受到干扰后,最大扰动幅值小且恢复时间短,说明其控制效果优秀,上升速度快,抗干扰能力强。

5 结束语

螺旋给料计量系统是一个复杂的非线性控制系统,系统的控制性能直接影响着加工产品的质量。随着市场变化,传统的PID控制越来越难以满足企业日益提高的产品精度要求。为提高螺旋给料计量系统的控制性能,本文结合先进的智能控制算法,借助遗传算法对模糊控制参数进行优化,进而获得优异的控制性能。通过仿真结果表明,相比于传统PID和模糊PID控制器,通过遗传算法优化的模糊PID控制器响应速度快,稳定性好,能保证螺旋给料计量系统给料的精度与鲁棒性。