深沟球轴承剥落故障动力学建模与仿真

陆 阳

(湖北工业大学机械工程学院, 湖北 武汉 430068)

深沟球轴承有动力传输效率较高、摩擦系数小等优点。根据统计,30%大型旋转设备故障和44%的异步电机中的故障与轴承相关,其中轴承的故障90%的位置位于内圈和外圈[1]。为了早期预测轴承故障,减低因此产生的经济损失,对于滚动轴承进行故障动力学建模并对其进行研究有重大意义。

Tang等[2]基于ANSYS建立滚动轴承有限元模型,通过有限元方法将滚动轴承内圈、外圈及各个构建之间的摩擦应力、应变等参数变化规律进行对比,验证有限元仿真的合理性。Patel等[3]构建了6自由度动力学模型,分工况研究了轴承内、外圈存在的单点和复合故障的振动响应特性。Petersen等[4]基于有限元模型,研究了滚动体缺陷,即在运动过程中滚动轴承内圈、外圈、滚动体及保持架等部件的接触力、轴承刚度及振动特性的变化情况。Patil等[5]利用Hertz接触理论对轴承构建间的接触关系建立模型,通过有限元更新单元的计算得到仿真信号,实现对轴承故障传动机械的模拟。刘湘楠等[6]提出了一种奇异值分解差分谱与S变换相结合的方式微弱冲击特征提取方法。孟宗等[7]提出的一种基于有效奇异分量的G-K奇异值分解字典学习方法,利用包含故障信息较多的分量对字典原子进行更新和系数求解。毛文涛等[8]基于深度迁移学习的早期在线检测方式,采用一种深度自编网络,构造出有改进的最大均值差异正则项,以扩大轴承在故障和正常状态下的差异,提高检测的准确性。

本文通过构建一个四自由度动力学模型来模拟仿真由剥落引起剥落点形成凹坑的单点故障。其尺寸大小:故障宽度为0.18 mm,故障深度为1 mm。轴承的故障位置位于轴承的内圈和外圈滚道。最后通过时域波形和频谱两个角度对模型的合理性进行验证。

1 滚动轴承动力学模型

1.1 滚动轴承建模简化条件

在深沟轴承建模的过程中,只研究内圈和转子的竖直位移y1和水平位移x1,轴承座和外圈的竖直位移y2和水平位移x2。为了对轴承故障状态更好地仿真,对轴承进行简化:1)只考虑轴承在xoy平面的力,内圈和转子绕z轴旋转,外圈不转动;2)滚珠与内外滚道之间的接触假设为Hertz接触;3)忽略润滑剂产生的阻尼和刚度问题;4)滚动体均匀分布在转子周围;5)滚动体在内、外滚道之间的运动为纯滚动且不考虑滚动体的离心力。根据上述假设,深沟球轴承的接触可以简化为四自由度仿真模型(图1)。

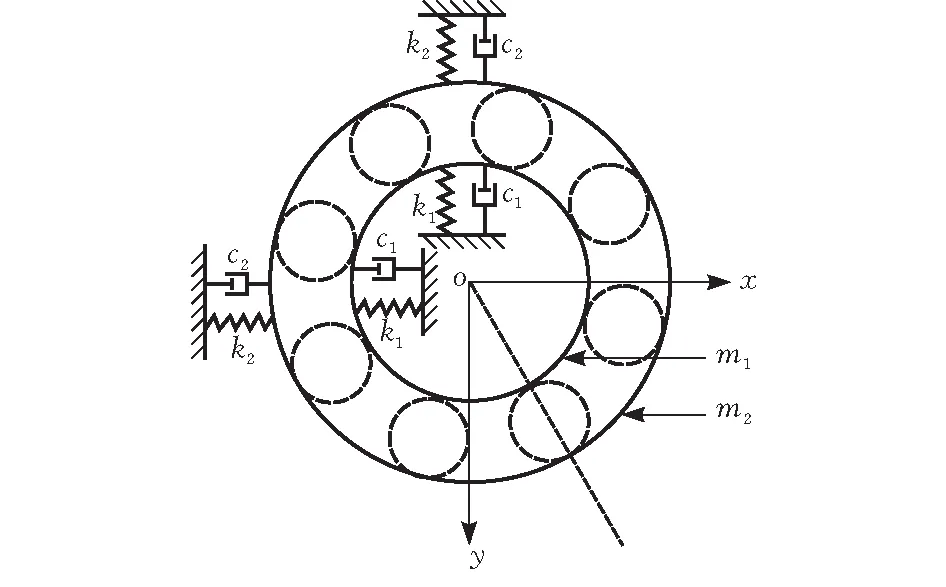
图1 滚动轴承四自由度系统

1.2 Hertz接触刚度计算

赫兹将轴承中滚珠与滚道之间的接触假设成线弹性体问题(图2),图3为轴承几何参数的示意图。

图2 Hertz接触示意图

由于轴承中内外滚道与滚珠相接触,滚动体为物体a,内外滚道为物体b,X平面为与滚动轴承径向平行的平面,Y平面与滚动轴承轴向平行的平面,则滚珠与内滚道接触的主半径

(1)

其中:Dj是内圈滚道直径,m;ri是内圈沟槽半径,m;rb为滚动体半径,m。

同样,物体(滚珠)a和物体b(外圈滚道)接触曲面主半径

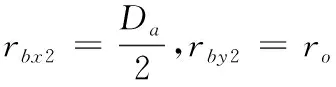
(2)

其中:ro为外圈沟道半径,m;Da为外圈滚道直径,m。

由于考虑到套圈挡边高度等因素,因此内外圈滚道直径计算公式为

Dj=Dj2-KdDb

(3)

Da=Da2+KdDb

(4)

其中:Kd为套圈挡边高度系数,Kd=0.35[9]。

根据实际情况,滚动轴承的内外圈滚道沟槽大于滚动体半径,ri和ro计算公式为

ri=kiDb

(5)

ro=koDb

(6)

式中:ko为外圈深沟曲率系数[9],ko=0.525[9];ki为内圈深沟曲率系数[9],ki=0.515[9]。

此外,还要考虑内、外圈与滚珠的接触刚度Kin和Kout,其计算式[10]:

(7)

(8)

式中:Ein和Eout是接触构件的等效弹性模量,接触面的泊松比和弹性模量是μ1,μ2和E1,E2,则等效弹性模量

(9)

根据式(7)和(8)中的其他参数[10]:

(10)

(11)

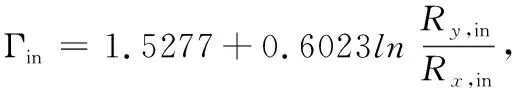
(12)

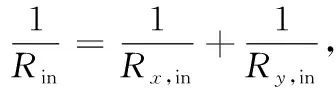
(13)

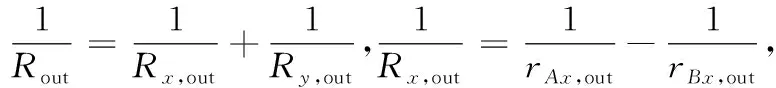
(14)

等效接触刚度K

(15)

等于深沟球轴承n=1.5[10]。

1.3 滚动轴承接触变形计算

内外圈的径向游隙和相对位移会对轴承中滚珠与内外圈接触变形有影响。在第i个滚珠处,由内外圈之间的相对位移造成的弹性变形

δi=(xin-xout)sinθi+(yin-yout)cosθi-cr

(16)

式中:θi为t时刻时第i个滚珠的角位置,rad;cr是轴承的径向游隙。

假如当θ1初始位置0时,滚动体个数为N,则

(17)

其中,ωc为保持架转动频率,rad/s。Dp为轴承节径,Db为滚动体直径,则

(18)

其中α为接触角,(°)。

当滚动轴承在运动过程中弹性变形大于0时,即内外圈能产生非线性弹性力。根据Hertz接触理论,任意的滚珠i所产生的恢复弹性力

(19)

其中,K为滚珠与轴承的内外圈等效接触刚度[10],N/m1.5。经过推算式(19)得到了x、y方向上的弹性恢复力

(20)

(21)

1.4 滚动轴承滚道局部故障建模

本文将模型中的故障假设为一个矩形凹坑(图4),故障深度为h,故障宽度是L。当滚珠运动到故障位置时,滚珠与滚道瞬时没有接触了;当滚珠离开故障位置时,构件之间的接触立刻恢复。滚珠i处的接触变形

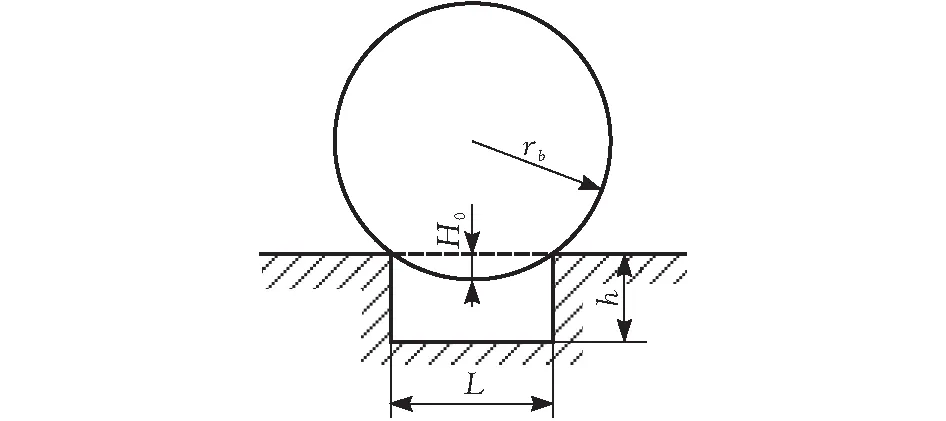
图4 故障形状对接触变形的影响

δi=(x1-x2)sinθi+(y1-y2)cosθi-cr-H

(22)

式中,H是引入故障。当滚动轴承在运转过程中会周期性地进入故障位置的距离,由于滚动轴承构件运动形式的不同,所以H的计算方式也有区别。

1)当内圈存在故障缺陷时,

(23)

式中:ψin是外圈故障对应的圆心角,rad。当Dj表示内圈直径,因为故障尺寸很小,所以

ψin=2L/Di

(24)

φin为内圈故障的角位置,因为内圈会随着转子一起转动,即:

φin=ωt

(25)

当故障位置是内圈时,H0是内圈与滚珠的圆心距,

(26)

2)当外圈存在故障缺陷时,

(27)

式中:ψout为外圈故障位置所对应的圆心角,外圈直径为Da,外圈故障时角位置

ψout≈2L/Do

(28)

当故障位置为轴承外圈时

(29)

1.5 滚珠随机滑动因素的引入

在滚动轴承实际工况中,每个滚珠受到周期性波动的载荷,因此会产生随机滑动。根据文献[11],滚珠i在t时刻的位置可表述为:

(30)

其中θr为滚珠相位角偏差。

1.6 建立动力学方程

基于模型简化和Hertz接触理论计算出接触变形和等效接触刚度建立如下动力学方程:

(31)

式中:t为时间,s;g为重力加速度,m/s2;ω为内圈转动的角频率,rad/s;e为偏心距,m;FH,x,FH,y为滚珠与内外圈产生的弹性恢复力在x,y方向的分量;k2为地面与基座的等效连接刚度,N/m;k1为轴和轴相连接处的等效连接刚度,N/m;c1为轴与固定处的连接阻尼,Ns/m;c2为地面基础固定与基座的连接阻尼,Ns/m;m1为轴和内圈的总质量,kg;m2为轴承座和外圈总质量,kg。

2 仿真分析

根据前面建立的动力学模型,求解之后可以获得系统的振动响应。本文对轴承SKF-6203-RS对平稳匀速旋转工况下进行仿真,采样频率为12 kHz,其几何参数如表1所示。根据前面的计算,轴承材料参数设置为:E1=E2=207 GPa,μ1=μ2=0.3。仿真参数如表2所示。

表1 轴承几何参数

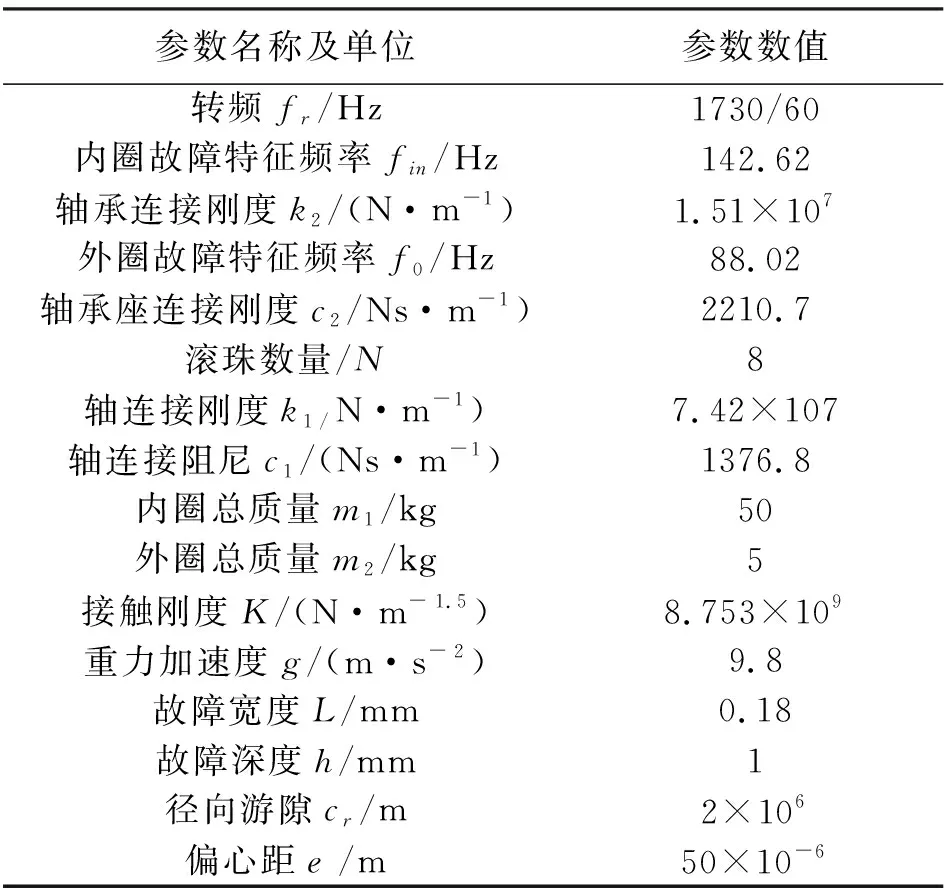
表2 滚动轴承仿真参数

2.1 外圈单点故障

在外圈滚道上建立一个槽型缺陷,故障宽度为0.18 mm,故障深度为1 mm,利用Matlab/Simulink搭建仿真模型,采用变步长ode45方法来求解动力学方程。图5和图6分别是模拟仿真的外圈故障振动信号的时域图和频域图。取时域信号长度3 s,频域的频率范围为0～500 Hz。从图5中可以看出时域上存在着周期冲击现象,图6频谱上特征缺陷频率88.16 Hz及其倍频清晰可见,且峰值随频率的增大而逐渐减小。

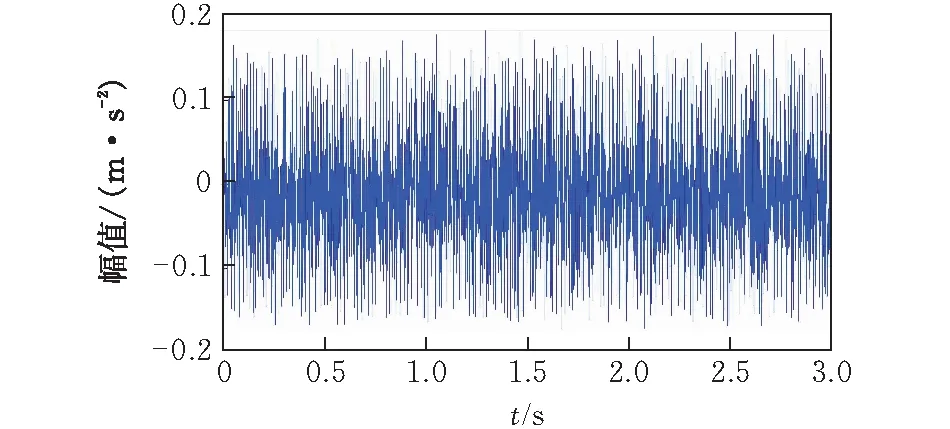
图5 外圈单点故障模拟时域

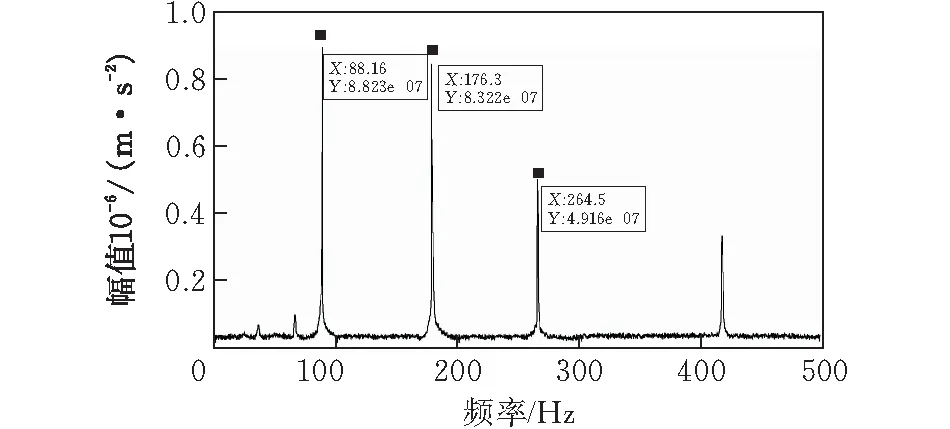
图6 外圈单点故障模拟频域

2.2 内圈单点故障

在内圈滚道上建立一个槽型缺陷,故障宽度为0.18 mm,故障深度为1 mm,用与外圈相同的方式求得,图7和图8分别模拟仿真的内圈故障振动信号的时域图和频域图。取时域信号长度3 s,频域的频率范围为0～500 Hz。从图7中可以看出时域上存在着周期冲击现象,从图8频域上可知轴的转频为28.78 Hz,特征缺陷频率为142.4 Hz,其倍频清晰可见,且峰值随频率的增大而逐渐减小。

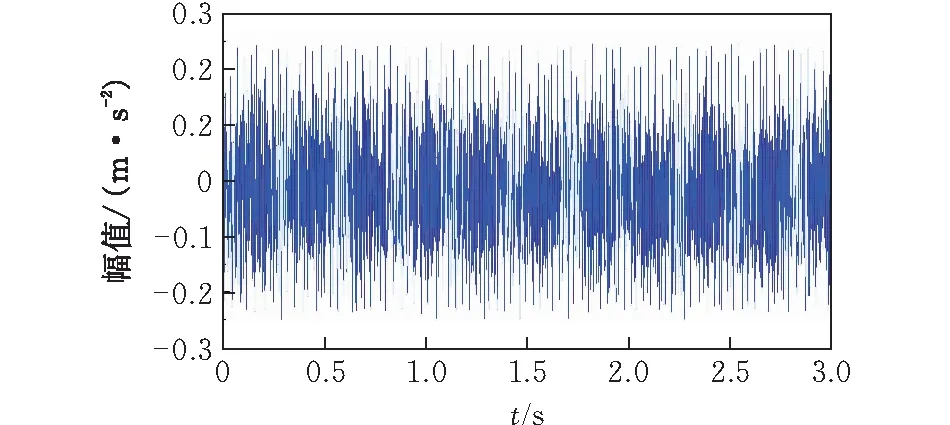
图7 内圈单点故障模拟时域

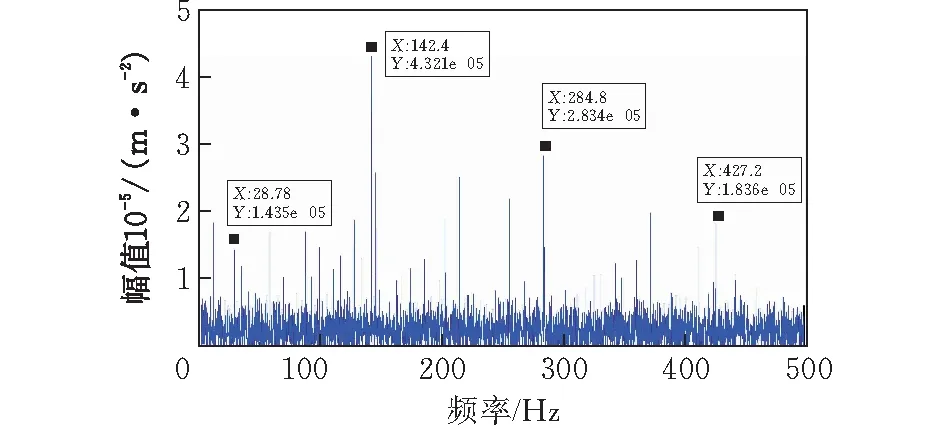
图8 内圈单点故障模拟频域

3 西储大学轴承实验

本文验证所用实际信号采集来自于凯斯西储大学的轴承实验,实验台如图9所示。平台由一个1.5 kW的电动机,一个编码器(扭矩传感器),以及电子控制器和功率测试计。电机的支撑轴承是测试轴承。驱动端滚动轴承型号为SKF-6205-RS,风扇端轴承型号为SKF-6203-RS,其几何参数如表1所示。

图9 凯斯西储大学轴承实验台

实验中的故障是用电火花加工的方式制作出单点损伤,实验中轴承的缺陷位置是内外滚道及滚动体,故障的尺寸直径为0.18 mm,0.36 mm,以及0.53 mm的凹坑。

选择风扇端轴承SKF-6203-RS,其转数为1730 r/min,采样频率为12 kHz,选用内外圈具有直径为0.18 mm单点故障时的信号作为实验验证信号,证明模型的合理性。

3.1 外圈单点故障实验验证及分析

当主轴转速为1730 r/min,缺陷尺寸为0.18 mm时,外圈单点故障的时域图和频域图分别如图10和图11所示。从图10可知,实验的外圈故障信号在频域上存在明显的周期性冲击现象;从图11可知,在频域上其特征缺陷频率为88.32 Hz及其倍频清晰可见。对比数据发现,实验数据与仿真数据基本吻合,具有较高的准确性,从而验证了本文所建模型的正确性。

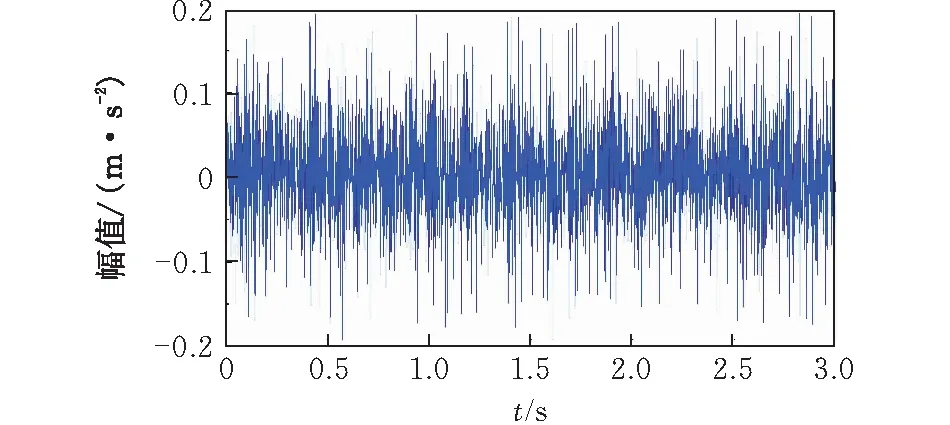
图10 0.18 mm外圈单点故障实验时域

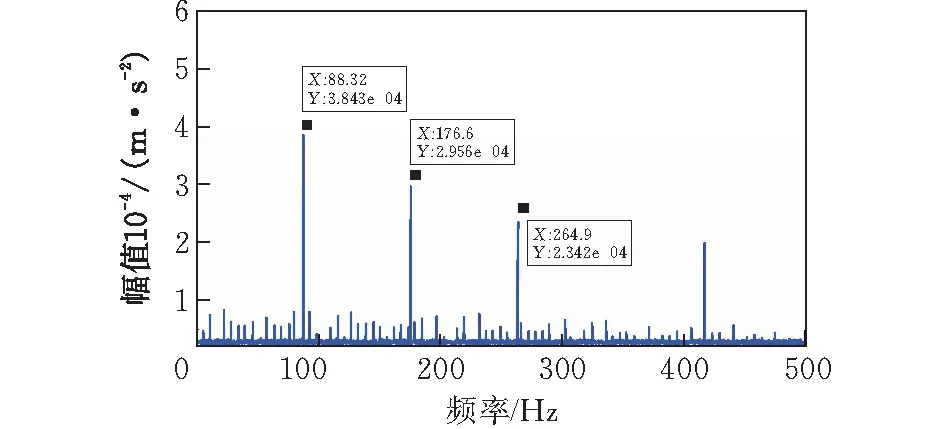
图11 0.18 mm外圈单点故障实验频域

3.2 内圈单点故障实验验证及分析

主轴转速为1730 r/min,缺陷尺寸为0.18 mm时内圈单点故障的时域图和频域图分别如图12和如图13所示。

图12 0.18 mm内圈单点故障实验时域

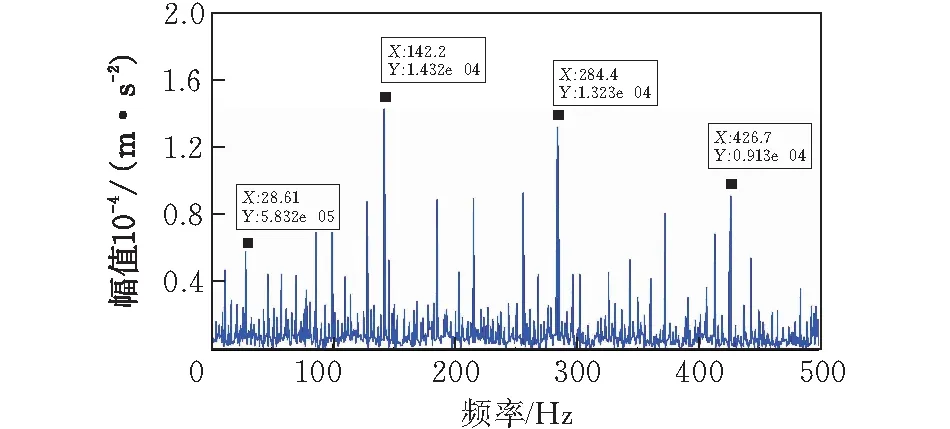
图13 0.18 mm内圈单点故障实验频域

从图12可知,实验的外圈故障信号在频域上存在明显的周期性冲击现象;从图13可知,在频域上转频为28.61 Hz、特征缺陷频率142.2 Hz及倍频和边频带清晰可见。对比数据发现,实验数据与仿真数据基本吻合,具有较高的准确性,从而验证了本文所建模型的正确性。