考虑工作连续性的重复性项目鲁棒调度优化

张立辉，郭欣雨，邹 鑫，曹蔷楠

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学经济管理系，河北保定 071003）

1 研究背景

重复性项目是指在建设工程的每个活动单元，各个子工序不断重复进行的项目，包括道路、桥梁、高层建筑、油气管道、风电、光伏电站等。关键路线法（critical path method，CPM）能有效解决一般性项目调度问题，但在进行重复性项目调度时存在一些缺陷，例如不能表示项目的空间位置、无法体现资源使用的连续性以及难以更新等［1］。为此，学者们提出了一些更适用于重复性项目的调度方法，平衡线法（line of balance，LOB）是其中应用较为广泛的方法之一。随着我国现代化进程的推进，在基础设施建设大发展的背景下，越来越多的重复性项目在进行规划和建设中，因而研究重复性项目调度问题具有较大的应用价值。

目前，国内外关于重复性项目调度问题的研究主要集中于确定性条件下的调度优化，包括资源分配、工期优化、时间费用权衡等问题，如Ammar［2-3］、Gouda 等［4］、Tran 等［5］、García-Nieves 等［6］、Podolski 等［7］的研究。然而，重复性项目具有规模大、工期长、参与主体多、工程环境复杂等特点，项目执行过程中的不确定性因素众多，容易造成项目成本增加、工期延误等问题。例如，南水北调工程在建设丹江口大坝的过程中，由于资金、水文环境等不确定因素的影响，完工时间延误长达50 多个月，索赔金额高达2.67 亿元［8］；港珠澳大桥在进行海底沉管隧道安装作业时，由于水面往来船只影响和海流转向等突发因素，仅沉管作业任务就延误了3 个月［9］。在此情况下，一个能够应对不确定性事件的进度计划对保障项目的顺利完工具有关键作用。

“鲁棒性”是现代控制理论中的重要概念，Al-Fawzan 等［10］最早将“鲁棒性”概念引入项目调度领域。为应对项目实施过程中的诸多不确定性因素，保证项目按时按计划完成，越来越多的国内外学者开始研究项目调度的鲁棒优化问题。例如，van de Vonder 等［11］将进度计划的鲁棒性分为质鲁棒性和解鲁棒性。质鲁棒性是指项目在截止日期内完成的稳定性，该研究通过项目按时完工率来衡量进度计划的质鲁棒性，如何立华等［12］则提出了以活动延期风险和前继工序数量为权重的质鲁棒性指标，建立了以加权时差和最大化为目标的优化模型，并通过算例验证了该指标的优越性。解鲁棒性是指项目进度计划的工序按计划时间开始的稳定性，如李雪等［13］构建了以成本最小化与解鲁棒性最大化为目标的多模式进度计划优化模型，利用项目活动缓冲时间的加权和度量进度计划的鲁棒性；庞南生等［14］采用活动的实际开始时间与计划开始时间的加权偏差度量解鲁棒性，以惩罚成本最小化为目标，设计了启发式算法来确定鲁棒性最优的资源分配方案；马志强等［15］针对活动可拆分项目，定义了资源流网络下自由时差的计算方式，提出了基于自由时差效用值的解鲁棒性指标，构建了鲁棒性最大的优化模型，并设计了遗传算法进行求解。然而，以上研究都是基于网络计划项目而展开的，而网络计划下的时差概念与重复性项目所建立的时差具有很大区别，因此还需要针对重复性项目特点进行鲁棒调度优化研究。

不确定环境下的项目调度研究可分为模糊调度、随机调度和鲁棒调度3 类［16］。模糊调度和随机调度采用概率和模糊理论来描述工序工期的不确定性，而重复性项目多为常规基础建设项目，其主要的不确定性来源于突发事件扰动而非工序工期不确定，且重复性项目对不确定性扰动十分敏感，受到扰动后极易导致中断和延误在项目内部传播。鲁棒调度能够针对突发事件的扰动制定根本性处理策略［17］，从而减少不确定扰动对重复性项目的影响，因此，鲁棒调度更适合于不确定环境下的重复性项目。但目前针对重复性项目鲁棒调度优化的研究还比较少。Zhang 等［18］首次将鲁棒性概念引入重复性项目调度中，建立了以资源使用量最小和鲁棒性最大为目标的优化模型，但是该模型没有考虑进度计划的质鲁棒性，且其采用的工序间断方法不能保证重复性项目工作连续性的要求。工作连续性是指重复性项目工序执行中全部或部分不能被打断，它是重复性项目的一个重要特点。根据Hyari 等［19］的研究可知，重复性项目需要保证工作连续性的原因如下：（1）实际工程中某些工艺或技术指标要求必须保持工序在各单元之间的施工连续；（2）减少资源闲置和浪费，避免一些额外成本；（3）减少解雇和重新雇用人员的需求；（4）最大限度地利用学习效应。

基于上述现实和理论背景，本研究根据工作连续性要求，结合时间缓冲区技术，通过设计鲁棒优化指标，研究工作连续性的重复性项目鲁棒调度优化问题。

2 适合重复性项目特点的时间缓冲方法和鲁棒优化指标

2.1 时间缓冲的位置

时间缓冲区技术是鲁棒调度应对不确定性的主要方法［20］，通过在进度计划中插入时间缓冲来吸收各种不确定性因素给各项活动执行造成的延误，以保证基准进度计划的稳定性。常用的方法有项目缓冲法和分散缓冲法［21］。项目缓冲法来源于关键链项目管理，通过在关键链结尾处插入项目缓冲以保证整个项目按时完成［22］，从而提高进度计划的质鲁棒性；分散缓冲法是通过分散地在各个工序间插入时间缓冲来保证项目按照基准进度计划执行，从而提高进度计划的解鲁棒性。目前尚未有研究将时间缓冲区技术应用于重复性项目进行鲁棒调度优化，而通过插入时间缓冲的方法可以在满足重复性项目工作连续性要求的同时提高进度计划的鲁棒性，十分契合重复性项目特点。

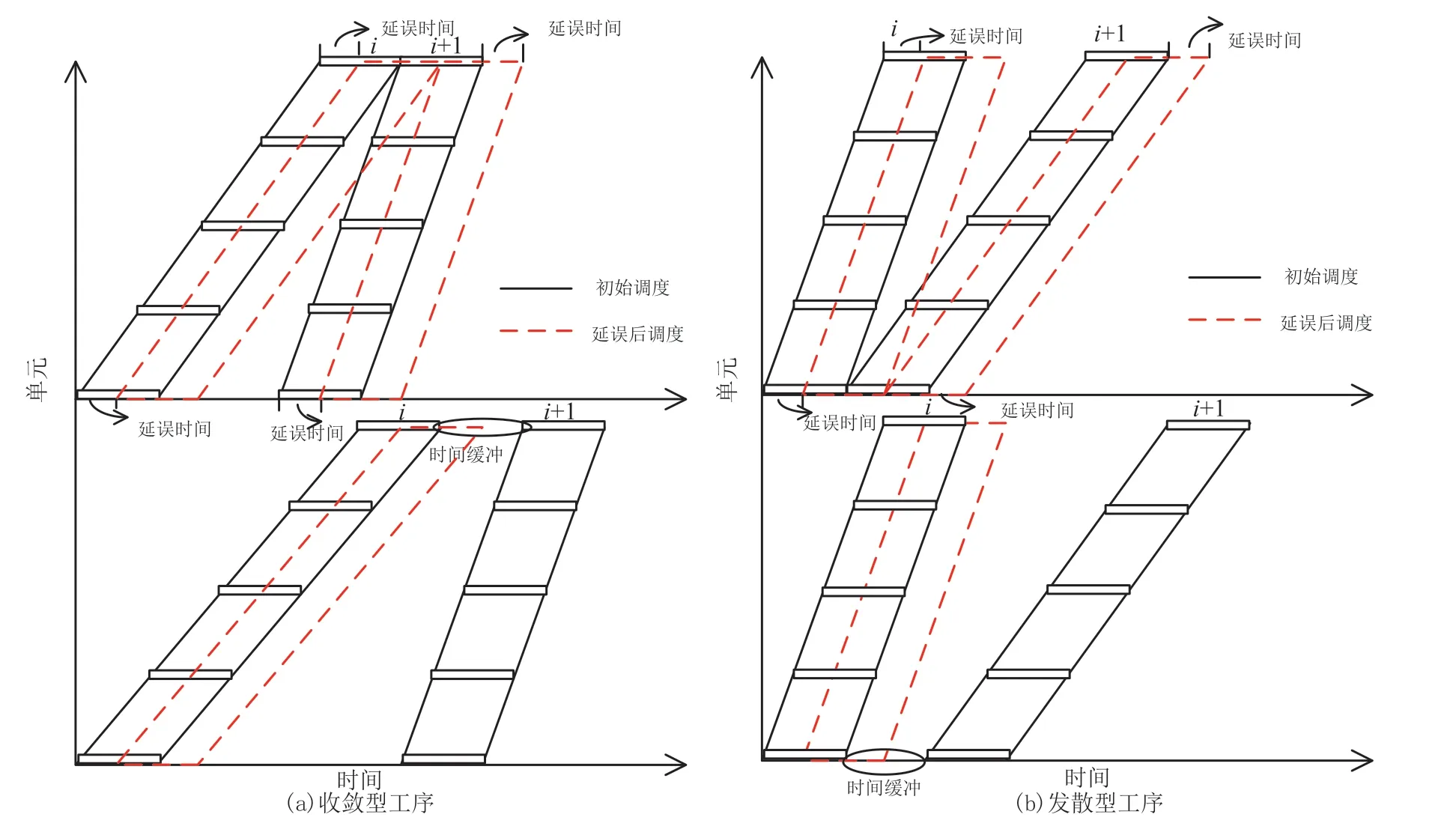
图1 重复性项目中吸收延误的时间缓冲方法

当两个工序之间呈收敛型关系时，在最后一个单元，紧后工序的开始时间由紧前工序的结束时间控制。由于工作连续性要求，紧前工序的任意一个单元发生延误都会造成此工序最后一个单元的延误，从而导致紧后工序所有未开工单元的开始时间发生延误，但如果计划阶段在紧前工序的最后一个单元后插入分散缓冲，可以使紧后工序各单元不受延误影响，从而起到吸收延误的作用。同理，当两个工序之间呈发散型关系时，在紧前工序的第一个单元后插入分散缓冲能够起到吸收延误的作用。为吸收整个项目的延误，在最后一道工序的最后一个单元和截止日期之间插入项目缓冲，分散缓冲和项目缓冲的位置如图2 所示。其中，分散缓冲和项目缓冲可表示如下：

图2 重复性项目吸收延误的缓冲位置

2.2 时间缓冲权重的设计思路

基于CPM 的鲁棒调度优化大多数采用紧后工序数量或后继工序数量作为鲁棒指标的权重，将时间缓冲优先分配给紧后或后继工序数量多的工序，但是，重复性项目中大多数工序为关键工序，仅不足30%的工序为非关键工序［23］，很多工序仅拥有一个紧前或紧后工序，如果使用紧前或紧后工序数量作为时间缓冲分配的权重，大部分工序的权重相等，并不能起到很好的优化作用；如果使用后继工序数量作为鲁棒优化指标的权重，会使时间缓冲集中分配给靠前的工序，而一般情况下，项目执行过程中越早开始的工序越容易把控，越晚开始的工序越容易因不确定因素影响而发生拖延［24］。这种情况下，一旦靠后的工序发生延误，将难以保证项目按时完工。针对重复性项目以上特点，除风险权重之外，选择前继工序数量作为鲁棒优化指标中分配时间缓冲的权重，将时间缓冲较多地分配给靠后的工序。这样会带来两方面的好处：（1）延误风险较大的工序（靠后的工序）能够获得更多的时间缓冲，保证项目进度计划具有一定的项目缓冲，从而提高进度计划的质鲁棒性；（2）当靠前的工序分配的时间缓冲不足以吸收延误时，可以通过后面的时间缓冲来吸收延误，实现时间缓冲的共享。

2.3 鲁棒优化指标设计

Lambrechts 等［25］指出活动拥有的时差的数量与项目进度计划的鲁棒性呈一种非线性关系，时差数量的增加对鲁棒性增强的贡献是边际递减的，因此提出了基于时差效应函数的鲁棒性度量指标。张静文等［26］认为使用时差效用函数可以使时差在各个活动之间的分布更为分散，以避免时差仅分配给某几个活动，从而增强进度计划的鲁棒性。一般而言，越多的活动拥有时间缓冲，进度计划的鲁棒性越高。结合重复性项目的工作连续性特点，通过时差效用函数来实现时间缓冲的合理分配，并构建重复性项目鲁棒优化指标，目标函数如式（3）所示，表示最大化进度计划鲁棒性。

3 鲁棒优化模型构建与求解

3.1 模型构建

将式（4）（5）代入式（3），可得

（2）工作连续性约束。在重复性项目中，工序i的生产率表达形式如下所示：

为满足工作连续性要求，在LOB 中任意工序的最后一个单元的开始时间，可以由第一个单元的开始时间确定。在确定工序i的生产率之后，工序i的最后一个单元m的开始时间可以由式（8）确定。

（3）优先关系约束。假设工序之间为最常见的“结束-开始”（FS）关系，考虑插入时间缓冲后，应满足式（11）（12）。

（4）截止日期约束。通常，项目需在截止日期内完成，而重复性项目的结束时间由最后一道工序中最后一个单元的完成时间决定，若添加项目缓冲，那么加上项目缓冲时间后的项目结束时间应处于截止日期内。

（5）资源约束。在重复性项目建设中存在资源约束，即每个工序都存在工作队雇佣数量的上限，该约束如式（14）所示：

3.2 求解步骤

由于鲁棒优化模型是混合整数线性规划模型（MILP），MILP 问题属于NP 困难问题［28］，所以程序可能不会在合理的时间内终止，因此，限制程序最长运行时间；如果程序能够自行停止，那么得到问题的最优解，否则将得到一个近似最优解。针对问题特点，使用MATLAB YALMIP 工具箱调用CPLEX 对鲁棒优化模型进行求解。具体步骤如下。

步骤2：根据初始调度计划计算所有工序自身拥有的分散缓冲和项目缓冲，并设置每个工序插入缓冲天数的上限。

4 算例分析

采用某高速公路工程实例进行案例分析。该项目共有24 道工序，每道工序包括10 个子单元，项目合同工期为238 天。增加考虑了工序所面临的延误风险大小，采用1～9 标度法对不同工序可能遭受的延误风险进行评判，其中1 表示工序遭受延误的风险程度最低，9 表示工序遭受延误的风险程度最高，并对所有工序的风险权重进行归一化处理。为保证进度计划拥有项目缓冲，最后一道工序设置一个较大的风险权重。其他项目相关信息如表1 所示。

表1 鲁棒优化前后案例工程相关数据比较

首先，根据项目信息，以工期最小为目标制定初始进度计划，初始进度计划的完工时间为199 天；其次，由于每道工序之间缺少时间缓冲，一旦有延误情况发生，项目将无法按照初始进度计划进行，因而进行鲁棒调度优化；最后，通过鲁棒优化模型求解，得到如图3 所示的鲁棒进度计划，进行优化后每道工序所需工作队数量、每道工序后插入时间缓冲数量如表1 所示。

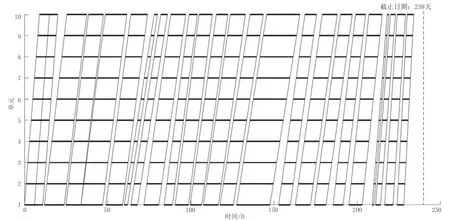
图3 案例工程的鲁棒优化进度计划

由算例结果可知，鲁棒进度计划的完工时间为238 天，仍在合同工期之内；进行优化后一共插入39 天时间缓冲，其中有22 道工序之后插入了时间缓冲，最后一道工序之后插入了4 天项目缓冲。为进一步检验基于鲁棒优化模型的鲁棒优化效果，通过蒙特卡洛模拟进行解鲁棒性和质鲁棒性检验。

4.1 解鲁棒性检验

在检验解鲁棒性时，将初始进度计划记作调度1，将基于鲁棒优化模型得到的进度计划记作调度2，采用Zhang 等［18］的设计方法，将各活动实际开始时间偏离计划开始时间之和R1作为检验指标。R1越大表明在项目执行过程中需要进行的调整越多，即解鲁棒性越差。

式（15）中：Si为工序在进度计划中的计划开始时间；为工序的实际开始时间。

采用蒙特卡洛法模拟工程项目在实际执行中可能遭遇的工期延误，随机模拟进度计划受到干扰的次数分别为10 次、30 次、50 次和70 次，对10 000次模拟得到的R1取平均值，记为，所得结果如图4 所示。可知：（1）偏离计划开始时间之和随着受干扰次数的增加而增加；（2）调度2 的偏离计划开始时间之和明显小于调度1，并且随着受干扰次数的增加，这种差距越来越明显。这说明调度2 在一定程度上提高了进度计划的抗风险能力，具有一定的解鲁棒性。这是由于，通过时差效用函数合理地将分散缓冲分配在各个工序之间，使进度计划具有一定的抵抗不确定性干扰的能力，验证了基于鲁棒优化模型提出的时间缓冲分配方案的合理性。上述结果说明，鲁棒优化模型可以有效地提高进度计划的解鲁棒性。

图4 案例工程进度计划的解鲁棒性蒙特卡洛检验统计结果

4.2 质鲁棒性检验

在检验进度计划的质鲁棒性时，为验证本研究设置的以前继工序数量作为重复性项目分配时间缓冲权重的合理性，将其分别与以后继工序和以紧前工序作为插入时间缓冲权重的进度计划进行对比，将以后继工序作为插入时间缓冲权重的进度计划记作调度3，以紧前工序作为插入时间缓冲权重的进度计划记作调度4，以项目按时完工率R2作为检验指标。由于项目工程的延误时间具有不确定性，且单元工期越长的工序延期的可能性越大，假设延误时间服从自由度为2 的卡方分布，子单元工期延误总数为100 次，并随机生成发生延误的子单元位置，模拟项目执行10 000 次，调度2 和调度3 的工期频率分布如图5 所示。结果显示，调度2 的项目按时完工率为100%，调度3 的项目按时完工率为53.31%，调度4 的按时完工率为31.30%，调度2 的质鲁棒性明显优于调度3 和调度4。该结果说明，以前继工序数量作为鲁棒性优化权重，可以有效地通过插入项目缓冲来提高进度计划的质鲁棒性。

图5 案例工程的蒙特卡洛模拟工期频率分布

上述结果表明，鲁棒优化模型可以实现在工序之间合理地添加分散缓冲，并在项目完工后添加项目缓冲，从而得到一个更为稳健的进度计划。综上所述，本研究所提出的鲁棒优化指标和模型非常适合重复性项目，具有可行性和有效性，可以在最大化进度计划的解鲁棒性的同时提高质鲁棒性，在每个工序都保持连续性的基础上增强了进度计划的抗风险能力。

5 结论

本研究对象为不确定环境下重复性项目鲁棒优化问题，考虑重复性项目工作连续性要求，将时间缓冲区技术应用于重复性项目的鲁棒调度优化，并设计了适合重复性项目特点的鲁棒优化指标，在此基础上构建了鲁棒优化模型并进行求解。工程实例分析和蒙特卡洛模拟结果表明，本研究提出的模型可以保持工序的连续性，并在工序之间合理地添加分散缓冲和项目缓冲，从而保证进度计划的质鲁棒性和解鲁棒性，可为重复项目管理者建立具有稳定性的进度计划提供决策支持。由于前摄性调度不可能考虑到所有可能的干扰，需要进行反应性调度处理项目执行过程中前摄性调度无法预估的事件导致的进度扰动，笔者后续将研究重复性项目的反应性调度问题。