2022年甲卷理数客观压轴题的探究及启示
王东海
(安徽省肥东县城关中学,安徽 合肥 231600)
好的试题来之不易,它需要命题老师源于教材,又要高于教材,要注重基础性、创新性,还要立足于考查考生的关键能力和数学学科核心素养.
1 真题呈现

A.c>b>aB.b>a>c
C.a>b>cD.a>c>b
分析此题中三数的数值差距极小,如采用常规的作差法、作商法比较大小,则难以奏效.观察其结构特点,可尝试构造函数,再辅之求导判断其单调性进行比较大小.
2 解法探究


则f′(x)=-x+sinx,f″(x)=-1+cosx≤0.
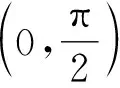
从而f′(x) 故f(x) 即a 因为g′(x)=-xsinx<0, 则g(x) 即xcosx 所以b 综上,c>b>a.故选A. 探求思路2这里比较大小时使用了构造法,而构造的函数不是唯一的,可以构造多种函数. 从而f′(x) 故有f(x) 即a 设g(x)=tanx-x, 所以g(x)>g(0)=0. 故tanx>x. 所以c>b. 综上,c>b>a. 探求思路3 此题出现的几个式子都与sinx、cosx有关,这里还可以考虑利用sinx、cosx的放缩不等式尝试比较大小[1]. 解法3 由三角函数线的知识可得放缩不等式 即a 所以c>b. 综上,a 故选A. 评注这类放缩不等式平时都会有所涉及,只要我们能够足够重视,运用起来就会得心应手. 探求思路4 函数的泰勒展开式,对于比较大小往往会化繁为简. 解法4 根据泰勒公式,知 而由泰勒公式,知 水行政立法执法工作不断加强。完成了《大连市节约用水条例(草案)》制订工作。开展了打击“涉河违法行为”专项执法行动,共完成河道采砂巡查45次,立案51起,清除行洪障碍25万m3,全市水事秩序进一步好转。 从而a 故选A. 评注泰勒公式虽是估值计算,但对解决选填题的比较大小问题,不失为一种快速有效的方法. 从而nsinx>nxcosx. 也就是说,我们可以将具有任意阶导数的函数展开成一个多项式函数,而高中所学的基本初等函数在定义域内大都具有任意阶导数.对于一些常见函数的泰勒展开式,在教学中要求学生尽量记住,如 此式两边求导,得 A.a C.c 解析根据泰勒公式,知 由此而知, 综上,c A.a C.b 故a=2ln(1+0.01) 综上所述,b 题3设函数f(x)=ex-1-x-ax2≥0对x∈[0,+∞)恒成立,求实数a的取值范围. 解析因为f(x)=ex-1-x-ax2≥0, 所以ex≥1+x+ax2. 当a≤0.5时,显然函数f(x)=ex-1-x-ax2≥0对x∈[0,+∞)恒成立. 故a≤0.5. 上面这三道高考题的解法运用到了高等数学中的部分知识,事实上近年来的高考题往往有高等数学的身影,如高等数学中的泰勒级数、洛必达法则、拉格朗日中值定理、函数的凸凹性、空间解析几何等.学生若是掌握了这部分知识可以很快给出答案.因此想考高分的同学,尽量还是要掌握一点大学的知识,笔者平时的教学也会根据学生情况进行分层教学,适当渗透一些高等数学的知识,如让学有余力的学生记住常用函数泰勒展开式、拐点等,并教会他们如何去运用[2]. 2022年高考数学全国甲卷第12题是一道对思维能力有较高要求的好题,但它并不是无本之源,而是与教材有着紧密的联系,正是贯彻了高考命题源于教材、高于教材的理念.此题的通解通法是构造函数,然后判断单调性即可. 考题是以此课本习题为蓝本进行命题的.因此笔者在平时的实际教学中也非常重视对课本例习题的挖掘,尤其是对教材中的“好题”的挖掘,所谓好题,就是指蕴含丰富的数学思想、开阔的思路、广阔的切入点的课本例习题.针对这些好题,要挖掘其中的高等数学背景,剖析背后的数学本质,感悟试题设计所蕴含的数学思想等,这样才能为高考打好基础. 4.3.1选择素材,一题多解 从这次的高考数学来看,光靠题海战术,靠大量刷题是行不通的,它对学生的关键能力和创新思维有着要求,随着新高考的逐步落地,高考评价体系也在逐步完善,推动着高考命题由能力立意向素养导向的变革,近年来的高考全国卷在题型、情景、设问方式等方面不断进行改革,导致新高考阅读量和灵活度增大.高三备考复习课上,虽然教师有基本方法的小结,但学生往往无法上升到解题能力的提升,这就容易造成复习时间长、效率低、进度慢的局面.而在复习中精选素材开展“一题多解”教学则能开拓学生的解题思路,并引导学生从多种解法的对比中选出最佳解法,使学生分析问题、解决问题的能力得到提高.因此在实际教学中既要重点讲解通解通法,也要适当渗透其它一些解题方法,这样才能培养学生的发散思维. 4.3.2培养编题,重视探究



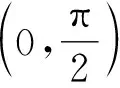

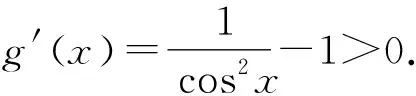
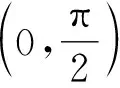






3 推广拓展


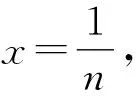
4 几点启示
4.1 背景分析
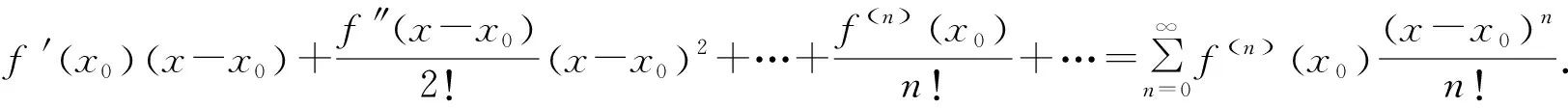
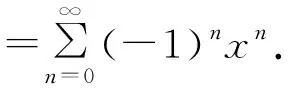
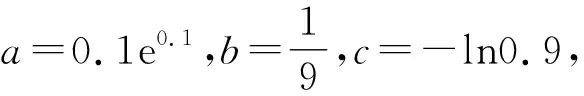


4.2 追本溯源
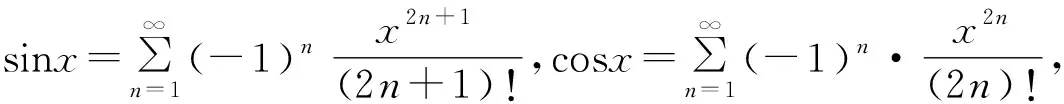
4.3 教学感悟