基于流形学习的红松仁脂肪近红外定量检测
仇逊超,曹 军,张怡卓
(1.哈尔滨金融学院 计算机系,黑龙江 哈尔滨 150030; 2.东北林业大学 机电工程学院,黑龙江 哈尔滨 150040)
我国是名副其实的松子产量和出口大国,约占全球松子交易量的77%,其中东北地区的产量占比达全国的90%左右,又以东北红松籽最为著名。红松仁富含亚油酸、亚麻酸等不饱和脂肪酸,具有降低胆固醇、血液黏稠,预防心绞痛、动脉粥样硬化、老年性肥胖症,提高脑细胞活性等功效,因此,红松籽有“长生果”的美誉。然而红松仁的油脂酸败会使其气味、色泽发生改变,影响其品质,缩短其存储周期。索氏提取法是种子脂肪含量测定的普遍首选标准方法,但其耗时长、步骤繁琐,且需要使用对人体有害的乙醚试剂,仅适用于严苛的实验室环境,无法满足大规模检测自动化及普及化的需求[1]。近红外光谱间接检测技术具有安全、简便、准确、快速、非破坏性、稳定性好等优点,且脂肪化学键在近红外光谱频段反应良好,因此,近年来近红外光谱技术被广泛地应用到坚果、肉类、谷物、乳类等农产品脂肪定量检测研究中[2-6]。
红松仁脂肪近红外检测研究还没有广泛开展,作者前期利用反向间隔偏最小二乘法、间隔偏最小二乘法、无信息变量消除法,构建了红松仁近红外特征筛选偏最小二乘脂肪定量预测模型。近红外光谱数据具有信息量过剩、特征间相关性较高、高维数据建模运算量大且耗时长等问题,除采用特征筛选来影响建模效率及模型预测的准确性外,还可以采用数据降维的方法来实现。数据降维具有保留信息本质结构的特点,降维方法分为线性和非线性两种,其中,线性降维方法无法很好地保留高维数据复杂结构的完整信息[7]。从数学拓扑出发的流形学习是一种非线性降维方法,其原理是寻找到低维流形模型到高维欧式空间的映射,尽可能地保留全部数据信息,表征数据的某些本质结构,并发掘数据的隐含信息[8]。
以红松仁脂肪含量为研究对象,提出一种流形学习的近红外光谱检测方法。运用变量标准化校正、一阶导数、小波变换对获取到的红松仁近红外光谱原始数据进行预处理,在此基础上,分别采用主成分分析的线性降维方法及等距映射、局部线性嵌入、改进型局部线性嵌入、局部切空间对齐、黑塞特征映射的流形学习非线性降维方法进行降维处理,以近红外技术中最为广泛采用的偏最小二乘为定标模型,比对岭回归、支持向量回归、极度梯度提升的建模结果,最终,找到最优近红外模型,实现对红松仁脂肪的无损、准确定量检测。
1 材料与方法
1.1 样本采集
本研究的红松籽样本购买于试验当年的凉水国家级自然保护区。对红松籽进行手工去壳脱红衣,随机选取390粒完整的红松仁样本,并进行159份的划分,其中,将134份样本分别放入贴有1~134编号标签的密封袋中;另25份样本分别放入贴有测1-测25编号标签的密封袋中,用于建模后对模型的测试。样本置于相对湿度和温度分别为50%~60%、-1~2 ℃的恒湿恒温阴凉处进行保存待用。
1.2 近红外光谱数据的采集
经查找相关文献发现,光谱波长范围在950~1 700 nm包含的信息可以较理想地满足本研究需求[9-10]。本研究采用德国INSION公司微型NIR-NT-spectrometer-OEM-system光纤光谱仪进行样本近红外数据的采集,该仪器具有高集成性和抗震性,其光谱适用波长范围为900~1 700 nm,光谱分辨率在16 nm以下。在采集样本近红外光谱数据前,先将红松仁样本置于环境温度为26 ℃左右的环境下24 h以上,打开预热光谱仪15 min左右,设置光谱仪积分时间为30 ms,平均次数设置为3次,将探头放入操作台底端的孔洞内,保持探头与样本距离在3 mm左右,固定探头。采集近红外光谱数据时,将倒卵状三角形的红松仁平滑腹部置于圆孔固定夹上。近红外光谱采集系统如图1所示。
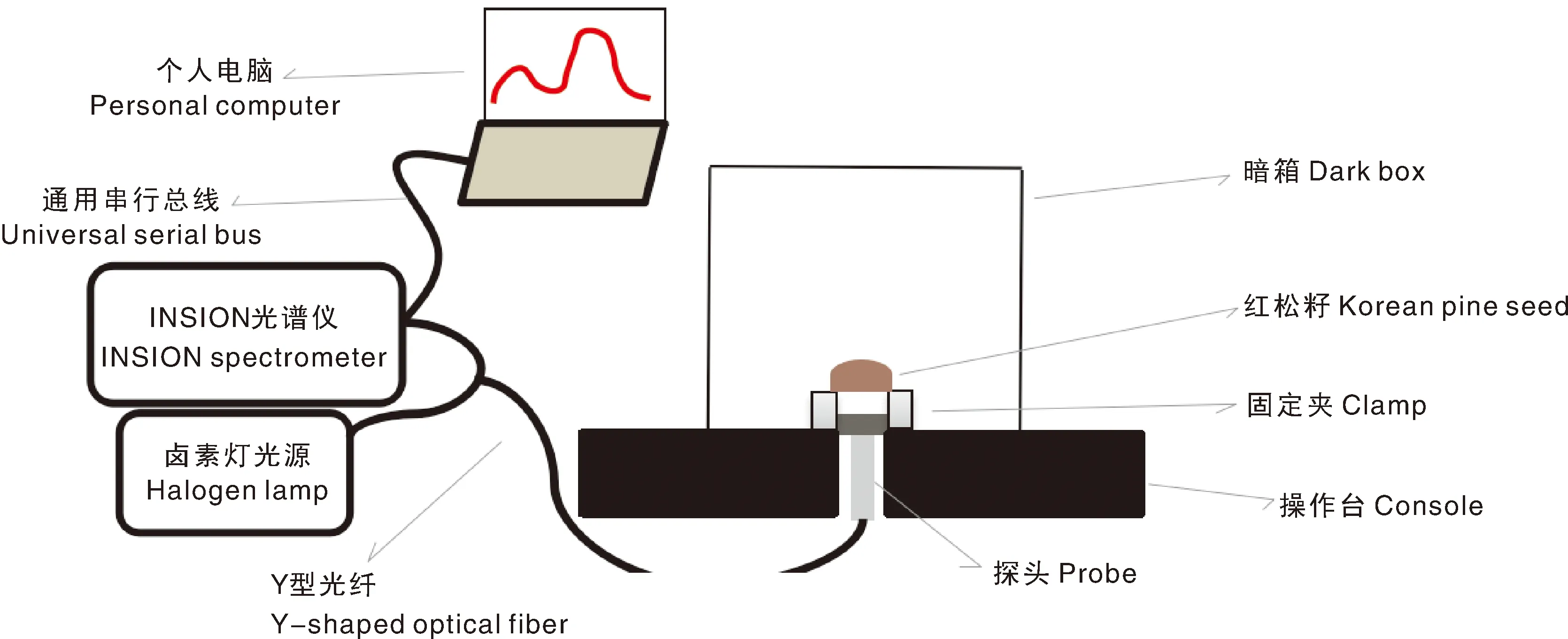
图1 近红外光谱采集系统示意图Fig.1 Schematic diagram of near-infrared spectrum acquisition system
1.3 化学脂肪真实值定量测定
红松仁脂肪的定量测定采用GB5009.6—2003索氏提取法。
1.4 流形学习数据降维方法
采用以下几种流形学习及改进型非线性降维方法,对红松仁近红外光谱数据进行降维处理。
1.4.1 局部线性嵌入及其改进方法
局部线性嵌入(locally linear embedding, LLE)[11]的中心思想是,找到每个数据点的原始高维领域线性关系表达后,在经过LLE降维处理后,在低维空间这种线性关系表达得到同样的保持,且这种表达的权重系数保持不变。假设高维空间数据点xi的邻域线性关系表达式为:
xi=ωihxh+ωikxk+ωilxl。
(1)
其中,ωih,ωik,ωil为权重系数,权重系数ωij可以通过式(2)求取:
(2)
其中,Q(i)表示数据xi的n个邻域数据点集合,m表示样本个数。保持ωij不变,低维空间数据点yi通过式(3)求取:
(3)
基于上述LLE思想,进一步衍生出了改进型局部线性嵌入(modified locally linear embedding, MLLE)、局部切空间对齐(local tangent space alignment, LTSA)、黑塞特征映射(Hessian based locally linear embedding, HLLE)方法。
MLLE不仅寻找最近距离的邻域数,还对邻域的分布权重进行度量,希望邻域的分布权重尽量在样本的各个方向。LTSA则是希望在降维后,局部邻域的几何关系仍能得到保持。HLLE是依据黑森矩阵的二次型关系展开构建,以达到恢复邻域内局部线性结构的目的。
1.4.2 等距映射方法
等距映射(isometric mapping, Isomap)是线性降维多维缩放(multi-dimensional scaling, MDS)的扩展,与保持局部结构信息的LLE不同,该方法对全局的信息进行保存,使得高维数据点对间的测地距离在降维后的低维空间中得以保持不变[12]。
2 结果与分析
2.1 红松仁漫反射近红外光谱数据分析
图2所示为红松仁样本近红外原始光谱曲线图,实际采集的光谱波长范围为906.9~1 699.18 nm,扫描间隔为6.83 nm。
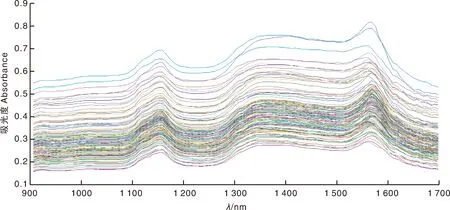
图2 红松仁原始近红外光谱曲线图Fig.2 Original near-infrared spectrum curve graph of peeled Korean pine seeds
脂肪是由脂肪酸和甘油组成的甘油酯,其化学元素主要为C、H、O,其CH、CH2、CH3群中的C—H键吸收谱带被用于近红外光谱脂肪检测中的特征吸收波段[13]。图2中920 nm附近的不明显吸收峰为C—H伸缩振动能级跃迁所引起的倍频和合频[14],1 160 nm附近的强烈吸收峰为C—H二级倍频伸缩振动基频,1 380 nm附近的明显吸收峰为C—H一级倍频伸缩振动基频与C—H变形振动基频组合频,1 670 nm附近的微弱吸收峰为C—H一级倍频伸缩振动基频[15];脂肪C—H基团的吸收谱带分布在900~1 020 nm、1 070~1 440 nm、1 520~1 680 nm[16-17]。通过上述分析可知,本研究选取的光谱范围可以反映红松仁脂肪的相关特征信息。
2.2 脂肪真实值数据分析
红松仁样本脂肪分布情况如图3所示,脂肪含量在60.04%~69.93%,虚线内样本占总样本的55.22%,分布差异较大,基本覆盖了红松仁脂肪含量常规分布范围,表明了样本选取合理,能够满足后续的建模要求。

61.14%为均值-标准差,65.58%为均值+标准差。61.14% was the result of mean minus standard deviation, and 65.58% was the result of mean plus standard deviation.图3 红松仁样本脂肪含量分布情况Fig.3 Distribution of fat content in peeled Korean pine seeds
2.3 训练集与验证集的划分
训练集与验证集10次切分结果如表1所示。
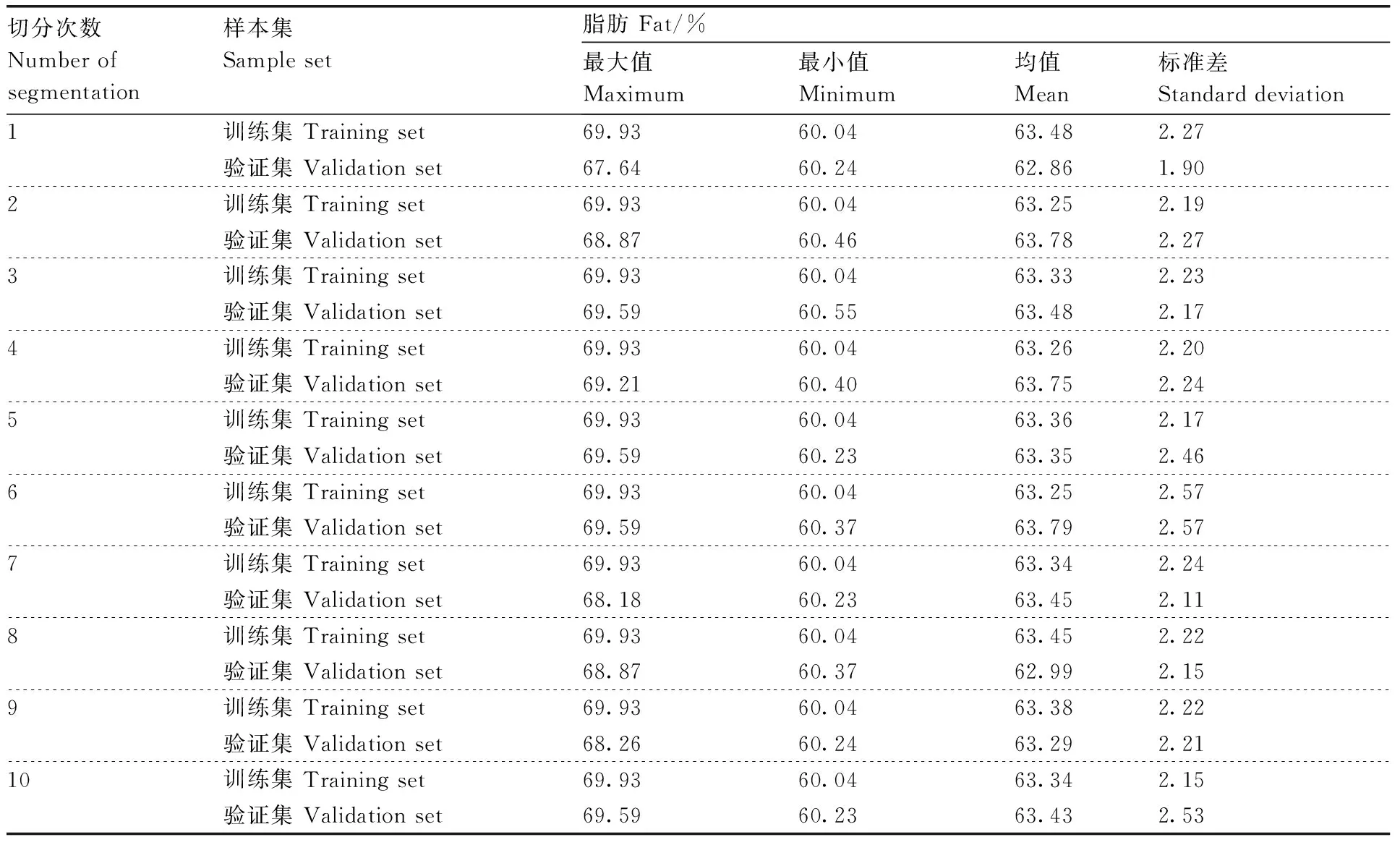
表1 十次红松仁脂肪训练集和验证集切分结果Table 1 Ten times segmentation results of fat in peeled Korean pine seeds’ training and validation sets
为了测试本研究构建模型的稳定性与可靠性,按照4∶1的比例对训练集与验证集进行10次不同划分,将10个固定取值的随机种子与10次划分结果相对应,以保证划分结果的可重复性。分别在不同训练集上,进行10次近红外红松仁脂肪定量模型的建立,以10次模型的平均评价指标来评估模型。观察表1发现,10次划分结果均不相同,且每次验证集脂肪含量覆盖范围均小于训练集,说明10个红松仁训练集样本所建立的模型可以较好地适用于相应的验证集样本。
2.4 光谱数据预处理
由于红松仁样本为固体,样本的颗粒度不均匀,且采用漫反射技术进行测定会使得光谱数据因散射影响而产生差异;观察原始光谱曲线图(图2),发现原始光谱数据的吸收宽度分散,且存在重叠现象,会互相干扰,影响模型的稳健性,因此,采用变量标准化校正(standard normalized variate, SNV)+一阶导数(first derivative, 1st-Der)对原始光谱数据进行预处理[18]。但经过求导处理后,会增加噪声、降低信噪比,因此,再进一步进行小波变换平滑处理。近似对称的紧支集正交小波(SymletN, SymN),能够在对信号进行分析与重构时减少相位失真,在对近红外光谱进行滤除噪声方面有较为广泛的应用[19-20]。采用Sym4小波基函数进行2尺度分解,则经SNV+1st-Der+Sym4预处理后的光谱曲线图如图4所示,观察发现,经预处理后光谱吸收峰增多且更为明显,光谱数据方差变小。随机选取一条滤波前后的光谱曲线,并将滤波后的光谱曲线向上平移一段距离,进行对比观察,如图5所示。由图5可知,经Sym4小波变换处理后,光谱曲线变得较为平滑,去掉了一些毛躁噪声,达到了一定的滤噪目的。
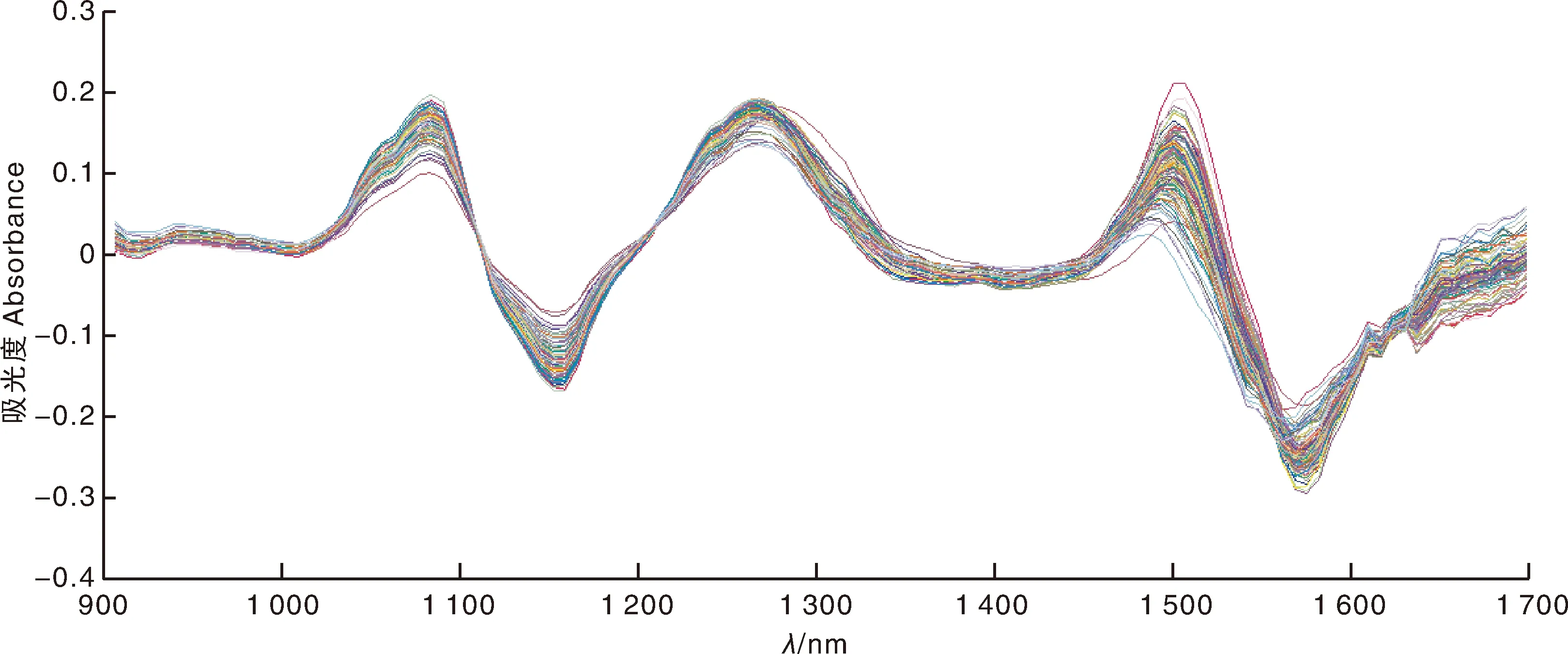
图4 变量标准化校正+一阶导数+紧支集正交小波变换预处理后红松仁光谱曲线图Fig.4 Spectrum curve graph of peeled Korean pine seeds after standard normalized variate+first derivative+orthogonal and compactly supported wavelet transformation pretreatment
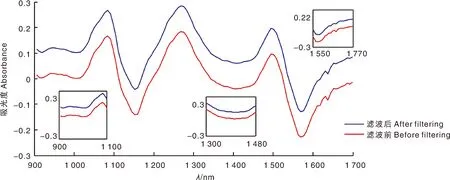
图5 滤波前后红松仁光谱对比Fig.5 Spectral comparison of peeled Korean pine seeds before and after filtering
图6所示为经预处理后的光谱数据特征热度图,由图6可知,经过预处理后特征间具有较高的线性相关性。
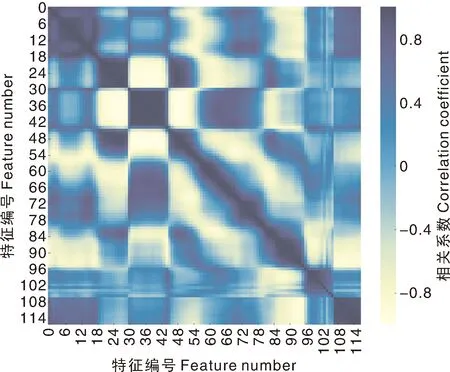
图6 预处理后光谱特征热度图Fig.6 The spectral signatures’ heat map after preprocessing
2.5 光谱数据的降维与建模
采用经典的线性主成分分析(principal components analysis,PCA)[21],及非线性流形学习中的Isomap、LLE、MLLE、LTSA、HLLE降维方法,在经预处理后的光谱上,进行数据降维处理。为了研究不同建模方法对红松仁脂肪定量预测模型的影响,进一步分别运用岭回归(ridge regression,Ridge)[22]、支持向量回归(support vector regression, SVR)[23]、极度梯度提升(extreme gradient boosting, XGBoost)[24]方法构建红松仁脂肪定量模型,并以偏最小二乘(partial least square, PLS)建立的模型为定标,根据模型的评价指标确定最优的降维及建模方法。
降维方法参数的不同取值,会对建模效果产生不同影响,因此,通过寻找最优降维参数,来进一步构建高质量的红松仁脂肪定量数学模型。
PCA需要对方差累计贡献率(contribution)进行最优参数的选取,通常规定累积贡献率需达到85%以上,因而其参数取值情况为:contribution=[0.85,0.86,0.88,0.90,0.92,0.94,0.96,0.98,0.99]。Isomap、LLE、MLLE、LTSA及HLLE需要确定邻域数(neighbors)和维度(components)的最优取值,其中,neighbors越大,降维后样本的局部关系会得到更好地保持,但算法的复杂度会增加,建立样本局部关系的耗时会更长,另外,neighbors最大取值不能超过红松仁训练集样本个数;MLLE需要满足:neighbors>components、HLLE需要满足:neighbors>[components×(components+3)]/2,因此将Isomap、LLE、MLLE、LTSA参数取值情况设置为:neighbors=[20,30,40,50,60,70,80,90,100]、components=[2,3,4,6,8,10,12,14,16,18];HLLE参数的设定分为以下几种情况,当components=[2,3,4]时,neighbors=[20,30,40,50,60,70,80,90,100];当components=6时,neighbors=[30,40,50,60,70,80,90,100];当components=8时,neighbors=[50,60,70,80,90,100];当components=10时,neighbors=[70,80,90,100];当components=12时,neighbors=100。
为了构建出一个高质量的PLS定标模型,需要对PLS主成分数(components)进行确定,根据方差累计贡献率在85%~99%的需求,主成分数取值范围为:components=[3,4,5,6,7,8,9,10,11,12,13,14,15,16]。根据比对10次不同切分出的10个验证集均方差(mean squared error of validation, MSEV)均值(mean-MSEV),确定最优的主成分数,比对结果如图7所示。
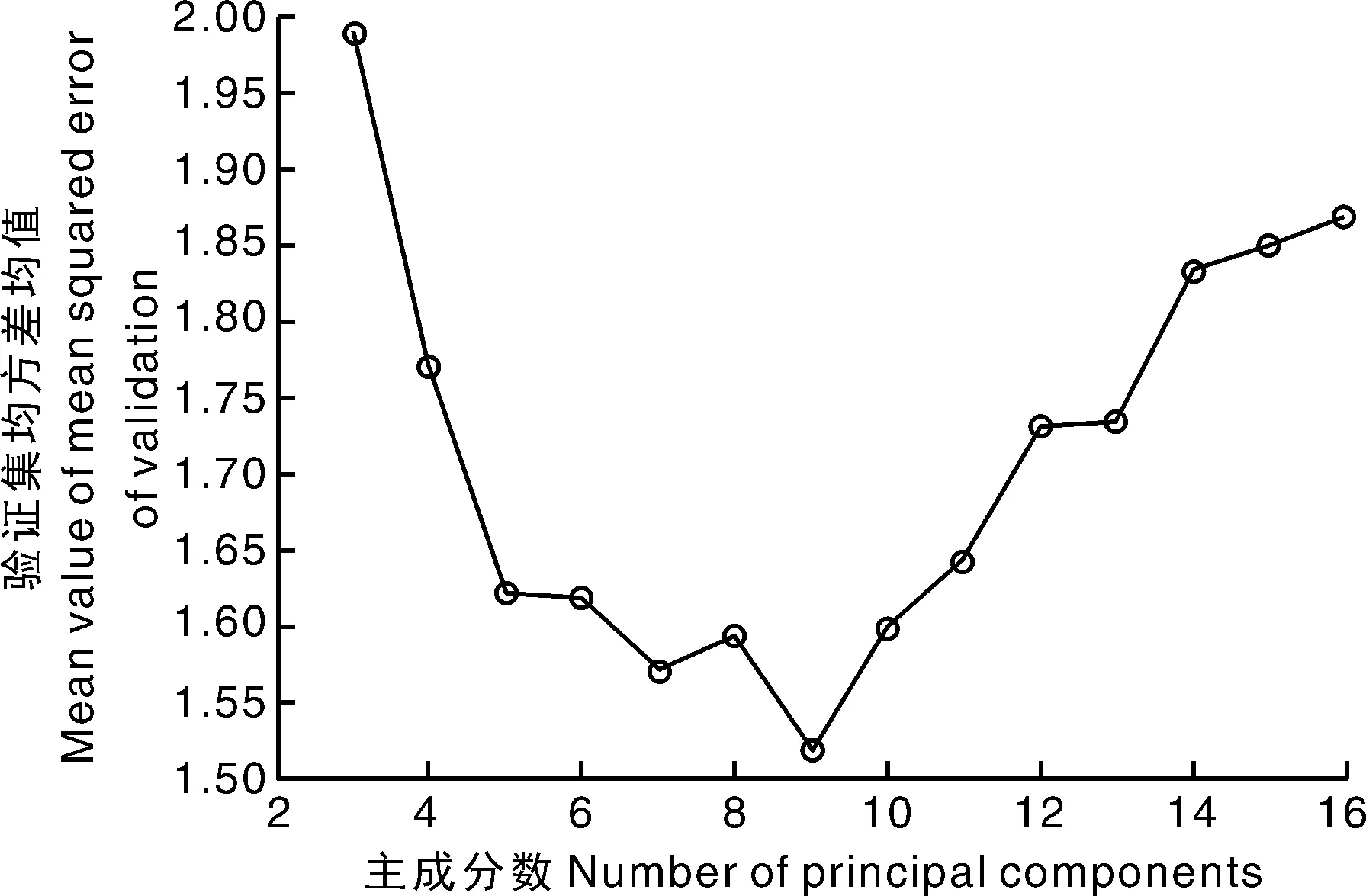
图7 Partial least square参数优化验证集均方差均值对比情况Fig.7 Comparison for partial least square’s parameter optimization of validation sets’ mean value of mean squared error
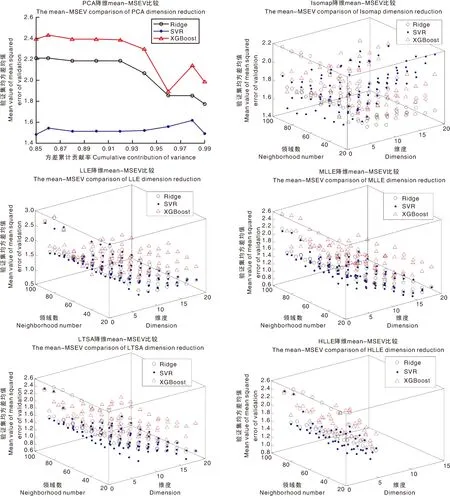
mean-MSEV值越小,拟合效果越好,则由图7可知,当components=9时,PLS模型质量最优,分别在全波段、光谱降维范围下构建红松仁脂肪Ridge、SVR、XGBoost、PCA+Ridge、PCA+SVR、PCA+XGBoost、LLE+Ridge、LLE+SVR、LLE+XGBoost、Isomap+Ridge、Isomap+SVR、Isomap+XGBoost、MLLE+Ridge、MLLE+SVR、MLLE+XGBoost、LTSA+Ridge、LTSA+SVR、LTSA+XGBoost、HLLE+Ridge、HLLE+SVR、HLLE+XGBoost数学模型,并对降维方法进行参数优化。为了测试模型的稳定性,每个模型会在10次不同切分出的10个训练集上进行模型构建,通过对比10次建模的mean-MSEV,从而确定降维、建模的选取方法,并找到相应降维方法的最优参数。对比情况如图8、图9所示。
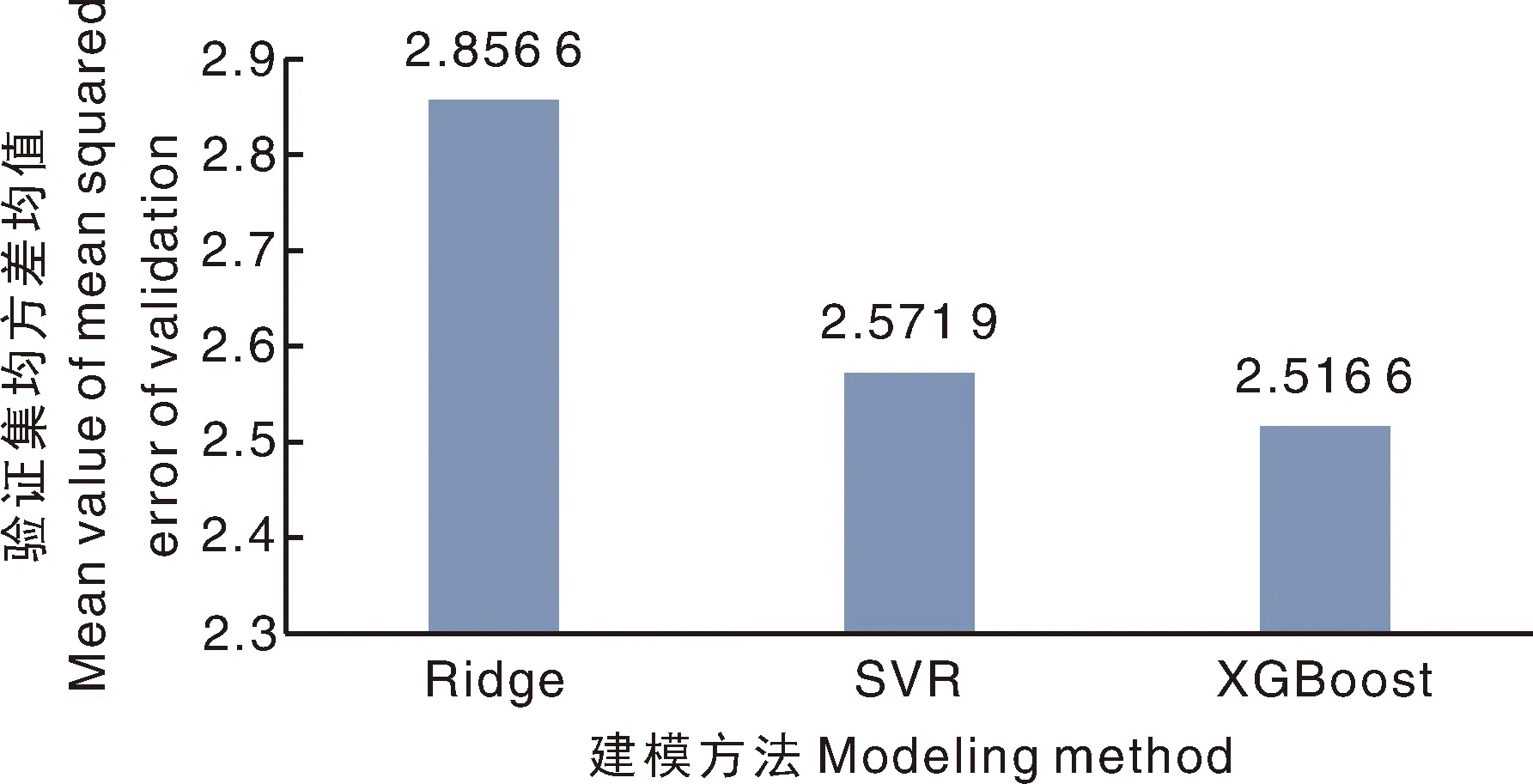
图8 全波段模型验证集均方差均值比较Fig.8 Comparison for full wavelengths of validation sets’ mean value of mean squared error
mean-MSEV,验证集均方差均值;Ridge,岭回归;SVR,支持向量回归;XGBoost,极度梯度提升;PCA,主成分分析;Isomap,等距映射;LLE,局部线性嵌入;MLLE,改进型局部线性嵌入;LTSA,局部切空间对齐;HLLE,黑塞特征映射。mean-MSEV, Mean value of mean squared error of validation; Ridge, Ridge regression; SVR, Support vector regression; XGBoost, Extreme gradient boosting; PCA, Principal components analysis; Isomap, Isometric mapping; LLE, Locally linear embedding; MLLE, Modified locally linear embedding; LTSA, Local tangent space alignment; HLLE, Hessian based locally linear embedding.图9 不同降维、建模方法及参数验证集均方差均值比较Fig.9 Comparison for different dimension reduction, modeling methods and parameters of validation sets’ mean value of mean squared error
其mean-MSEV为1.519 2,验证集皮尔森相关系数(Pearson correlation coefficient of validation, PCCV)均值(mean-PCCV)为0.813 3,mean-PCCV越接近1越好。通过定标模型可知,采用近红外光谱技术对红松仁脂肪进行定量分析是可行的,结果是可靠的。
由图8可知,不同建模方法构建出的模型质量不同,全波段范围内非线性模型XGBoost的建模效果最优,非线性模型SVR建模效果次优,Ridge则为线性模型,这说明红松仁光谱数据中,包含了对脂肪定量分析建模有用的非线性信息,而Ridge线性建模无法规划约束复杂的非线性问题。此外,由于PLS在建模过程中进行了PCA降维处理(图7),去除了冗余信息,因此其模型质量优于全波段范围下Ridge、SVR、XGBoost构建的数学模型。
图10为采用不同降维方法后,任意选取1个训练集的光谱特征热度图的对比情况,各热度图对应的降维参数分别为:PCA,contribution=0.99;Isomap、LLE、MLLE、LTSA,components=18,neighbors=100;HLLE,components=12,neighbors=100。
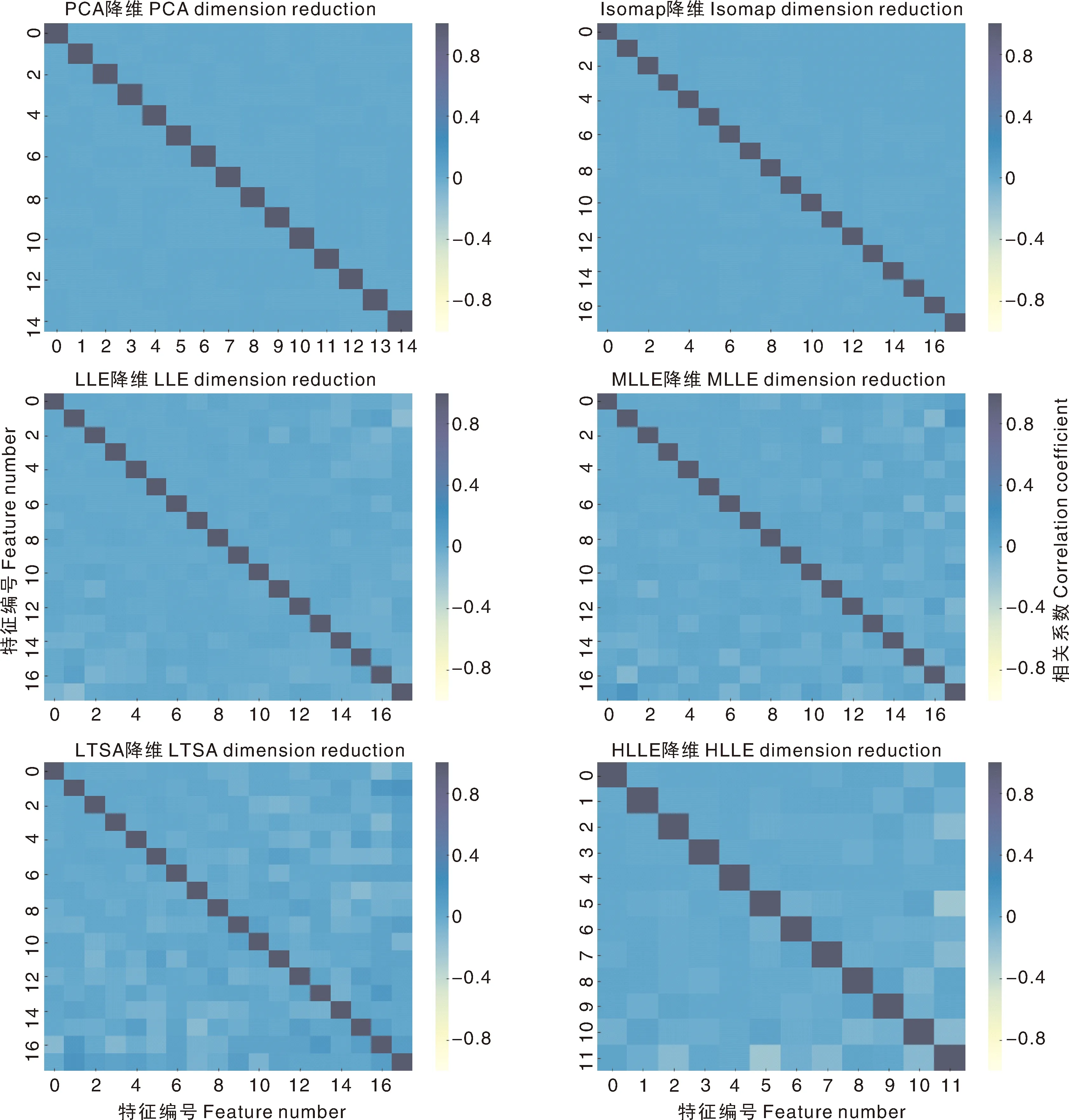
PCA,主成分分析;Isomap,等距映射;LLE,局部线性嵌入;MLLE,改进型局部线性嵌入;LTSA,局部切空间对齐;HLLE,黑塞特征映射。PCA, Principal components analysis; Isomap, Isometric mapping; LLE, Locally linear embedding; MLLE, Modified locally linear embedding; LTSA, Local tangent space alignment; HLLE, Hessian based locally linear embedding.图10 不同降维方法后光谱特征热度图对比Fig.10 The comparison of spectral signatures’ heat maps after different dimension reduction
由图10可知,经PCA、Isomap降维处理后,几乎完全去除了特征间的线性相关性;经LLE、MLLE、LTSA、HLLE降维处理后,还保留了部分线性相关性信息。由图9可知,与全波段构建的模型相比(图8),经过降维处理后模型的质量有所提升,这与图10结果相呼应,表明了特征间线性相关性较高会影响建模的效果。上述降维方法对Ridge与SVR模型质量的提升更为明显,这是因为XGBoost建模方法对数据维度具有相对较弱的敏感性[25]。为了更清晰地比较各最优参数模型质量,以表2形式进行呈现。
需要说明的是,由于10次切分出的训练集不同,因而依照方差累计贡献率的PCA降维方法,在不同训练集上降维后的维度会存在差异。
由表2可知,线性降维方法对模型质量的提升劣于非线性降维方法,这是由于经PCA降维处理后,会丢失非线性相关信息,无法较好地保留信息、估计潜在隐含信息的数量,这也表明了对本样本集来说非线性结构信息对脂肪定量建模效果的积极作用。流形学习中LLE及其改进降维方法对模型质量的提升优于Isomap方法,这是由于LLE及其改进降维方法更在意局部信息,能够更好地找到最优局部非线性嵌入,此外,通过图10可知,经LLE及其改进降维方法处理后,还保持了部分数据的局部线性特征,这些信息对本样本集红松仁脂肪含量的预测有较为重要的作用。相同建模方法采用LLE及其改进降维方法后,构建的模型质量相当但又略有不同,这是由于MLLE、LTSA、HLLE降维方法的基本思想均基于LLE降维方法,只是在低维数据进行恢复时遵循的优化原理不同,其中,Ridge、XGBoost分别经MLLE、LLE最优参数降维后,构建的模型质量最佳,mean-MSEV分别为0.709 3、0.989 5。
MLLE+SVR构建的模型质量最优,其10个验证集上的MSEV分别为:0.643 7、0.418 4、0.452 9、0.592 1、0.742 4、0.554 5、0.534 9、0.890 0、0.416 3、1.218 6,mean-MSEV为0.646 4,mean-PCCV达0.914 5,最优参数的取值为:components=16,neighbors=30。
2.6 模型的测试
采用最优参数的MLLE+SVR模型,对用于测试的25份红松仁样本脂肪进行定量预测,图11展示了化学实测值与预测值的散点分布情况。
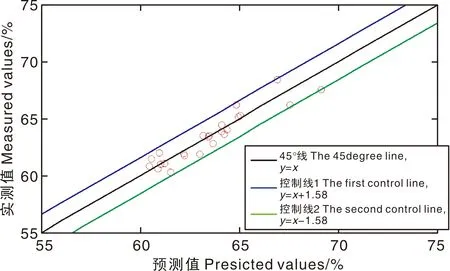
图11 红松仁脂肪实测值与预测值散点分布情况Fig.11 Scatter distribution of fat in peeled Korean pine seeds’ measured and predicted values
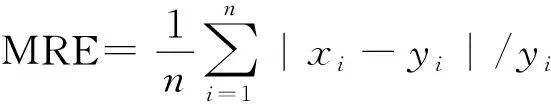
3 讨论
本研究通过在900~1 700 nm波长范围内对红松仁近红外光谱数据进行采集,开展了红松仁脂肪定量无损检测试验。在训练集与验证集划分的过程中,为了保障所建模型的可靠性与稳定性进行了10次不同的切分,并分别在10个不同的训练集上进行模型的建立,通过10个模型的平均评定指标来评价模型。采用降维方法对光谱数据进行降维处理,可以优化模型的评价指标,表明了光谱降维在模型训练中的重要作用;与线性降维方法相比,由于非线性降维方法可以更好地保留非线性信息及部分建模必须的特征间相关性信息,因此,非线性降维方法可以更好地提升模型质量。降维方法参数的取值也会影响模型的预测结果,参数优化可以有效地提高模型预测的准确性。运用不同建模方法构建数学模型,建模效果会存在很大差异,发现只有选取合适的建模方法才能构建出高质量的近红外模型。试验结果表明:(1)经过SNV+1st-Der+Sym4预处理后,光谱数据变得较为平滑,滤除了部分噪声信息的同时,也降低了光谱数据的分散程度。(2)经参数优化的MLLE+SVR,构建的红松仁脂肪定量预测模型质量最佳,降维方法优化参数取值为:components=16,neighbors=30,mean-MSEV为0.646 4,mean-PCCV达0.914 5。(3)运用最优参数模型,对选取的测试集25份红松仁样本进行脂肪定量预测,并与化学实测结果进行对比,通过计算得MRE=0.999 2%。由此可见,采用本研究方法对红松仁脂肪进行定量分析是可行的,并且预测结果是可靠的、准确的,期望通过本研究的实现,能够为红松仁脂肪定量检测提供一个新的方法和手段。

