改进粒子群算法和动态窗口法的动态路径规划

孙睿彤,袁庆霓,衣君辉,白 欢

(贵州大学 现代制造技术教育部重点实验室,贵阳550025)

1 概 述

路径规划是移动机器人技术中的重要研究方向之一.移动机器人的路径规划是指在静态环境或者是动态环境中规划出一条满足某种条件(通常是指最优的)的抵达目标点的无碰撞路径[1].良好的移动机器人路径规划技术可以应用于机器人探索人类无法到达的恶劣环境[2,3],也可以应用于智能仓储领域,减少人力物力,提高整体运输效率[4],是非常有意义的研究课题.

国内外都对移动机器人的路径规划算法有着深入研究,主要包括环境已知的全局路径规划和环境未知的局部路径规划.全局规划算法主要针对静态已知环境[5],提前进行地图构建,可以保证机器人以较短路径达到目标位置.常用的全局路径规划算法有智能仿生算法(遗传算法、蚁群算法、粒子群算法、蜂群算法(ABC)等)[6-8]、图搜索类算法(A*算法等)[9,10].局部路径规划是指机器人利用携带传感器采集的局部环境信息进行路径规划,具有实时性和灵活性,可用于未知环境,缺点是缺少全局性,宜陷入局部最优,主要包括动态窗口算法(DWA)、人工势场法等[11,12].全局路径规划和局部路径规划侧重点不同,前者进行实时避障,后者则统筹全局,旨在获得全局最优路径.想要获得效果显著的移动机器人的路径规划,需要将二者结合起来.

粒子群算法(PSO)因其结构简单,易于实现,广泛应用于路径规划中,但传统PSO算法存在收敛精度低,易早熟等缺陷[13].文献[14]提出了具有不同学习策略的自适应学习粒子群算法(SLPSO)来搜索最优或较优路径,文献[15]提出了负梯度和自适应粒子群优化算法(NGSPSO),相对其他算法具有更高的收敛精度和更快的收敛速度.但是仍未显著解决上述PSO算法的缺陷.而动态窗口法是经典的局部路径规划算法,可以进行实时避障,路径平滑,但是不具备全局性,甚至目标不可达[16].

针对粒子群算法收敛速度慢,以及只适用于静态环境的问题,和动态窗口算法不具备全局性的缺陷,对PSO算法进行改进,并提出一种改进的PSO算法与动态窗口算法混合的融合算法.该算法利用差分进化算法对粒子群算法进行优化,构造新的目标函数,实现对全局的路径规划,根据生成的路径提取局部关键点,再选择动态窗口算法实现局部路径规划,生成从起始点到目标点的最短且平滑的路径.

2 传统的PSO算法

Kennedy于1995年提出PSO算法[17],通过模仿鸟群觅食行为来搜索目标函数的全局最优值.PSO算法的路径规划问题本质上是优化问题.将每个粒子视为优化问题的一个解.对粒子赋予两个属性:位置和速度,在搜索空间里面控制粒子的运动,使得粒子向最优解方向移动.

设定目标搜索空间维度为D、种群的粒子数为N,则粒子i的位置是Xi=(xi1,xi2,…,xiD),i=1,2,…,N;粒子i的速度是Vi=(vi1,vi2,…,viD),i=1,2,…,N;粒子i所经历的个体最优位置是Pi=(pi1,pi2,…,piD);对整个粒子群进行判断后得到的全局最优位置是G=(g1,g2,…,gD).粒子速度和位置更新公式如下:

(1)

(2)

式中,w称为惯性权重[18],使算法在迭代过程中对先前迭代的惯性速度进行自适应调整.即随着迭代次数的增大,w随之减小,使得在迭代初期,有较大的搜索速度,提高算法搜索能力,保证算法效率;在迭代后期,搜索速度下降,提高搜索精度,具体公式如下:

(3)

(4)

(5)

3 算法改进

3.1 改进的PSO-DE算法

面向传统PSO算法因为结构本身缺陷而产生的易早熟,收敛速度慢等不足,本文利用结构简单,寻优能力强的差分进化(DE)算法[19],来促进PSO算法更好的寻找全局最优位置,提出一种改进的PSO-DE优化算法.

3.1.1 适应度函数设计

针对优化算法设计应用于路径规划中的适应度函数,基于实际需求,评价指标主要包括安全程度、路径长度两个因素.设置起始点Start坐标为P0,目标点Goal坐标为Pn+1,生成路径由Path={P0,P1,…,Pn,Pn+1}表示.

1)路径长度

路径长度函数f1用来计算移动机器人从起始点Start和目标点Goal之间的路径长度,可用式(6)来表示:

(6)

其中,(xi,yi)和(xi+1,yi+1)分别代表路径点Pi和Pi+1的位置坐标;

2)惩罚函数

移动机器人的路径规划在考虑从Start到Goal的路径长度的同时,要保证生成路径不会与障碍物发生碰撞.路径与障碍物相交次数越多,生成路径的危险程度越大.

将环境模型中的障碍物用圆形表示,m为障碍物数量.对于不规则障碍物,采用圆形近似处理.将障碍物半径设定为安全阈值记为R={rad0,rad1,…,radm},为获得无碰撞路径,需保证路径节点以及路径节点连线与障碍物的距离dis都大于安全阈值.路径节点为k个,ψ为危险性因子,对于穿过障碍物的节点判定为危险,给予惩罚,δ为权重系数,则惩罚函数为:

综上所述,应用于路径规划的适应度函数表达式为公式(7):

Fitness=f1+f2

(7)

3.1.2 改进的PSO-DE寻优机制

改进的PSO-DE寻优机制实现流程如下:

1)建立初始种群,维度为D,粒子数为N,初始化位置X,速度V;

3)根据表达式(1)、式(2)对X、V进行更新,生成优化的种群;

4)基于PSO算法生成的种群作为DE算法的初始种群,进行“变异”,“交叉”,“选择”3个操作;

5)DE算法的变异操作:

DE算法基于父代个体xi(t),i=1,2,…,n,随机选择个体进行差分变异,变异策略表示为“DE/子代生成方式/进行差分的组数/交叉方式”,本文选择DE/rand/1的策略:

hi(t)=xp1(t)+F·(xp2(t)-xp3(t))

(8)

其中,hi(t)为生成的变异向量;xp1(t),xp2(t),xp3(t)为种群在第t代中编号为p1,p2,p3的解向量,编号随机选取且与i两两互异;F为缩放因子,取值范围一般控制在(0,1.2];

6)DE算法的交叉操作:

父代向量xi(t),i=1,2,…,n以交叉概率Pc和变异向量hi(t)进行杂交,产生新的个体向量,成为试验向量vi,j(t),试验向量中的第j(j=1,2,…,D)维根据Pc在父代和变异向量中进行选择,公式如下:

(9)

式中:rand为[0,1]范围内的均匀随机数;Pc为交叉概率因子,Pc∈[0,1];jrand为[0,1]范围内的随机正整数,使得至少存在一个分量为变异向量产出,进而保证产生新向量;

7)DE算法的选择操作:

经过交叉变异操作后生成的向量vi(t+1)与父代向量xi(t)进行比较,保留适应度值(Fitness(*))较好的向量,公式如下:

(10)

8)根据5),6),7)得到DE算法下的最优位置与PSO算法生成的Gt进行比较,选择最小的进行更新;

9)输出全局最优路径Path={P0,P1,…,Pn,Pn+1}.

3.2 基于PSO-DE和动态窗口法的融合算法

改进的PSO-DE算法优化了全局路径规划的能力,但是仅针对静态环境,且路径存在尖点.动态窗口法是经典的局部路径规划算法,实用性强,但是易陷入局部最优,不具备全局性.本文在对PSO算法进行优化后,进一步采用动态窗口实现动态环境的实时避障,同时提高生成路径的平滑性,满足机器人的动力学性能,提出基于改进粒子群算法和动态窗口法的融合算法.

该融合算法的基本原理:利用PSO-DE算法生成全局路径,提取关键中节点作为动态窗口法的局部目标点,其中,影响生成路径平滑度的关键因子为航向角,本文在每次利用动态窗口法进行局部路径规划时令起始航向角继承上一次到达局部目标点的航向角,进而保证路径的平滑性.流程图如图1所示.

图1 融合算法流程图

具体实现流程如下:

1)提取全局路径生成的关键中节点{P0,P1,…,Pn+1}作为局部目标点,即每一次局部路径规划的起点为S{S1,S2,…,Sn}={P0,P1,…,Pn};每一次局部路径规划的局部目标点为G{G1,G2,…,Gn}={P1,P2,…,Pn+1},将路径划分成由{S1G1,S2G2,…,SnGn}组成的n段局部路径;

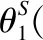
3)搭建机器人运动学模型

移动机器人的运动状态由速度空间(v,ω)进行描述.假设时间间隔Δt很小,机器人在Δt内即(t-t+1)内为匀速直线运动,则运动学模型如下:

(11)

其中,xt,xt+1分别表示移动机器人在t,t+1处的x坐标,yt,yt+1分别表示移动机器人在t,t+1处y坐标,θt,θt+1表示移动机器人在t,t+1处航向角,v表示线速度,ω表示角速度;

4)搭建机器人速度模型

运动学模型构建后,需进一步对速度进行求解,即建立速度求解模型.二维速度空间中存在无穷组(v,ω),需对其根据机器人实际情况进行约束,获得可行的速度范围:

(1)速度约束:

移动机器人速度受机器人本身能到达的或者是安全性因素下的最大最小速度制约,其速度约束空间用Vm表示:

Vm={(v,ω)|v∈[Vmin,Vmax],ω∈[ωmin,ωmax]}

(12)

式中,Vmin,Vmax,ωmin,ωmax表示移动机器人的最小,最大线速度和最小,最大角速度;

(2)动力学约束:

根据应用的移动机器人的电机性能不同,加减速度不同,故需要施加动力学性能约束,即:

(13)

式中,Vd表示动力学约束空间,vc,ωc表示移动机器人当前线速度,角速度;va,ωa表示最大加速度;vb,ωb表示最大减速度;

(3)制动距离约束:

为保证安全性,基于最大减速度要求,移动机器人在运动过程中需要保证在撞到障碍物前停止即速度减为0,Va表示制动距离约束空间,即:

(14)

式中,Dis(v,ω)表示(v,ω)对应的轨迹与障碍物之间的最小距离;

(4)构建DWA算法的目标函数

目标函数用来对在约束下生成的速度空间对应的轨迹进行评估,主要由与目标位置代价函数Head(v,ω)、与障碍物距离代价函数Obs(v,ω)、速度代价函数Vel(v,ω)组成,故目标函数即总代价函数Cost(v,ω)表达式如下:

Cost(v,ω)=αHead(v,ω)+βObs(v,ω)+γVel(v,ω)

(15)

式中,Head(v,ω)表示移动机器人与目标位置连线与当前位置航向之间夹角;Obs(v,ω)表示与障碍物最近距离;Vel(v,ω)表示当前模拟的速度代价;其中α,β,γ为加权系数;

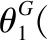
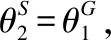
7)重复利用DWA算法对路径S3G3,…,SnGn依次进行局部路径规划;

8)记录每一段局部路径规划路线{S1G1,S2G2,…,SnGn},最后输出完整的最终路径.

4 实验结果与分析

本算法的实验环境为运行内存8GB的64 位WIN10操作系统,实验平台是集成的开发环境Anaconda3为保持良好的对比效果,在实验过程中,移动机器人的最大线速度、最小线速度、最大角速度、最大线加速度、最大角加速度、线速度分辨率、角速度分辨率、采样周期、向前预估时间等参数依次设定为:1.4m/s、0m/s(设置为不倒车)、40°/s、0.2m/s2、40°/s2、0.01m/s、0.1°/s、0.1s、3s.路径规划的起点与终点保持一致,分别为(0,0)、(10,10).

4.1 全局路径规划

试验1.本实验在场景1下进行,将算法与传统的PSO算法,ABC算法的路径规划结果进行对比分析,场景1为方形和圆形障碍物混合地图,共有10个障碍物,x和y的域值为[0,10].由于障碍物比较密集,选择路径节点数为3.利用经典测试函数对算法进行训练,确定改进的PSO-DE算法可以在较小的种群下寻找到最优结果,故而将所有算法种群大小设置为15,最大迭代次数设为100.

图2显示了几个算法的最佳路径,其中可以看到PSO算法和ABC算法的转折角更大,并且陷入了局部最优,PSO-DE算法生成的路径更为平滑.

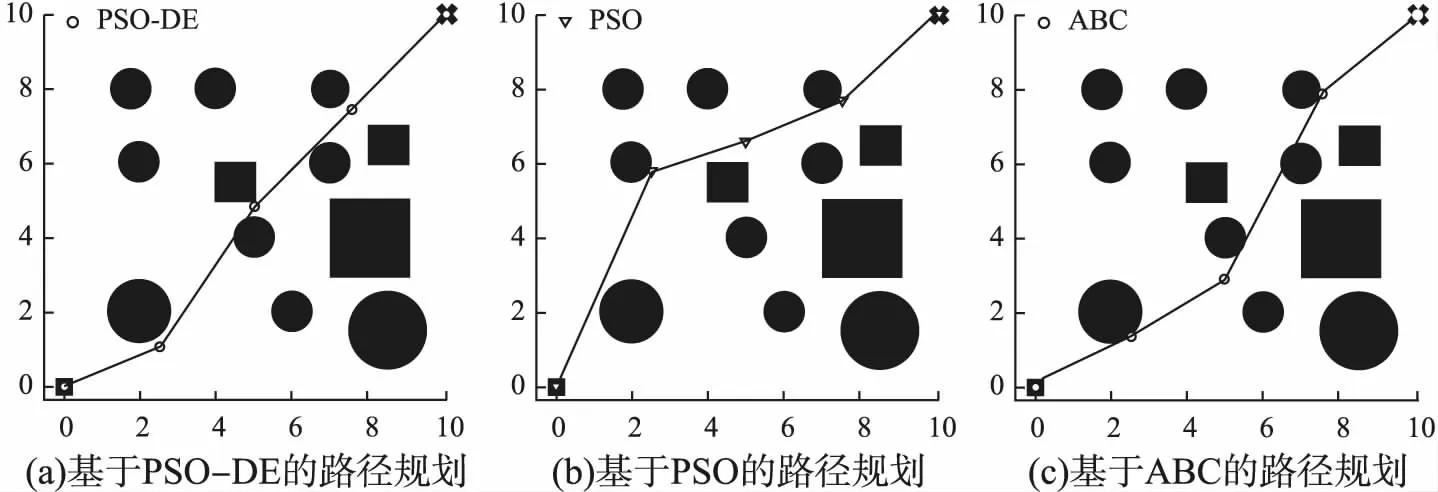
图2 场景1下所提算法与对比算法的路径结果比较

表1列出了20次运行结果的平均值(Mean),最佳适应度值(Best),最差适应度值(Worst)以及标准差(Std),可以看出,PSO-DE算法相较于传统的启发式算法具有更好的路径寻优能力,生成的路径长度最短,且标准差值Std较小,具有较好的稳定性.

表1 场景1下各算法进行路径规划结果

4.2 局部路径规划

实验1.本实验在场景2下对改进的PSO-DE和动态窗口法融合的算法进行试验验证并与传统的动态窗口法进行比较,场景2为动静障碍物混合地图,共有8个静态圆形障碍物和1个匀速向左运动的方形障碍物,x和y的域值为[0,10],Start为(0,0),Goal终点为(10,10).

图3可以看出运用动态窗口法得到的路径陷入局部最优,得到的不是最优路径,虽然路径平滑,但存在冗余路段.图4可以看出融合算法平滑性好,且路径更短,将路径从17.786缩短到14.691.融合算法改善了全局路径规划算法平滑性差,实时性不好的问题,同时改善了局部路径规划算法易陷入局部最优的缺陷,生成的路径符合机器人的运动学模型.

图3 场景2下动态窗口法路径规划

图4 场景2下改进融合算法的路径规划

实验2.基于场景2,增加了动态障碍物的数量对融合算法进行验证,观察算法可行性.如图5(a)所示,方形障碍物为动态障碍物,沿着x轴做循环往复运动,关键节点数量设为3,通过PSO-DE算法提取关键的局部目标点,进一步进行局部路径规划,如图5(b)所示,遇到动态的障碍物可以进行实时避障,图5(c)为完成第1阶段的局部路径规划示意图,完成路径规划后生成的最终路径如图5(d)所示.

图5 改进融合算法路径规划

将动态障碍物数量逐步增加来观察动态窗口法和改进的融合算法的路径规划能力,传统的DWA算法生成的路径长度如图6(a)所示,均大于改进的融合算法,随着障碍物增加逐渐增大,而如图6(b)所示的融合算法生成路径长度随着障碍物增加到2～3个时,路径长度增长缓慢,稳定性强.可以看出改进的融合算法可以在有效避障的同时寻找到最优的路径.

图6 随着动态障碍物数增加路径长度的变化

5 结 论

针对传统PSO算法存在的精度低、转折角多,只适用于静态环境,和传统动态窗口法效率低、易陷入局部最优等问题,本文提出基于优化的PSO-DE以及动态窗口法的融合算法,先通过改进的PSO-DE算法进行全局路径规划,生成关键中节点,再进行局部规划,可以成功进行动态障碍物的规避以及生成符合机器人动力学模型的最短平滑路径.经过大量实验证明该算法改善了传统PSO算法和动态窗口法的缺陷,对路径长度、平滑性、实时性等性能均有提高.本算法主要针对单移动机器人的在动态环境下的路径规划,下一步工作,将针对多移动机器人情况进行该算法的深入研究,解决智能仓储非结构环境下的机器人路径规划问题.