以用户体验为导向的空间众包任务分配研究

高丽萍,段普鸽,高 丽

1(上海理工大学 光电信息与计算机工程学院,上海 200093)

2(复旦大学 上海数据科学重点实验室,上海 200093)

3(上海理工大学 图书馆,上海 200093)

1 引 言

众包[1]作为一个大众人群积极参与其中的新型计算范式,已经融入到我们生活的各个领域.近年来随着互联网行业的快速发展以及移动设备的激增,传统的基于网络的众包正在转向具有很大发展前景的空间众包[2].任务分配[3]是空间众包平台面临的首要挑战.在空间众包中,工人需要亲自前往目标位置执行任务,因此,关于任务分配方法的很多研究都集中在最小化工人执行任务的出行成本上.然而,这些研究在计算工人出行成本时都只单单考虑距离的远近.现实情况是,工人对想要执行的任务地点的熟悉程度也很重要,这关乎到工人能否顺利到达指定地点,及时完成任务以及是否有良好的出行体验,目前很多研究工作没有考虑这一点.本文在计算工人到达任务地点所要花费的代价时综合考虑二者距离的长短以及工人对任务地点的熟知度两方面因素.

工人对将要执行的任务的偏好程度也被很多现有的任务分配方法忽略,然而除了出行成本,偏好也会影响工人在整个执行任务过程中的体验感.如果众包平台能投其所好,给工人分配到他比较想要执行的任务,工人就会有充足的动力,这样也会增强任务被顺利完成的可能性.另外,基于工人的意愿进行任务分配时还要考虑工人的声誉,声誉越高,表明工人越有把握成功完成任务.而且对于请求者来说,但凡是提交到众包平台上的任务,都希望得到预期的结果,将任务分配给声誉高的工人更能保证结果质量.因此在设计任务分配方案时引入声誉值既考虑到了工人执行任务的积极性,又保障了请求者的利益.

综上,本文提出一个以用户体验为导向的空间任务分配问题并建立最大化任务被成功完成的可能性分配(MPA)模型.MPA模型考虑了工人的出行成本,工人对任务的偏好度以及工人执行任务累积的声誉值3方面因素,基于此模型产生的任务分配方案对工人和请求者都是有利的.对于工人来说,MPA模型充分考虑了其在执行任务时会考量的因素,选择积极性高的工人执行相关任务,这样也能保证任务完成的质量和效率.从长远来看,能吸引更多的人参与到空间众包任务的执行中来.对于请求者来说,MPA任务分配模型能够尽可能使其获得期望的结果.总之,本文的目标是让众包系统的所有利益相关者,即工作人员、请求者和平台都被兼顾到.本文还提出改进的模拟退火算法,即MPS-SA算法智能搜索最佳分配方案以最大化全局概率分数.最后,在真实数据集和仿真数据集上通过与其他算法的比较验证了MPS-SA算法的有效性.

2 相关工作

近年来,关于空间众包任务分配的研究有很多.Tong[4]等人首次提出空间众包的全局在线微任务分配问题(GOMA),其中,任务和工人可以随机地动态出现.Zhao[5]等人提出基于工人时间偏好的空间众包任物分配系统,设计了偏好感知的个体任务分配算法,随后又提出将每个任务分配给一组工人的策略优化了原来的框架.

一般来说,空间众包平台在进行任务分配时,要实现一定的优化目标,如最大化分配任务的总数或最小化平台的招募成本.Liu[6]等人提出了两个双目标优化问题—FPMT问题(工人少,任务多)和MPFT(工人多,任务少)问题.FPMT问题的目标是最大化完成任务的数量和最小化工人的总行驶距离,而MPFT问题的目标是最小化平台的总支付报酬和最小化工人的总行驶距离.Zhang[7]等人使用工人置信度来表示成功完成所分配任务的可靠性,提出了招聘预算约束下的最大化可靠性分配问题(MRA)和任务可靠性要求下的最小化成本分配问题(MCA)并分别构建优化函数.

由于空间众包的特性,工人与任务之间的距离成为任务分配的重要度量指标.gMission[8]平台是一个典型的空间众包平台,其主要工作是获得用户的位置信息然后据此推荐任务.在推荐任务时平台只考虑距离的远近,也就是说,任务常常被推荐给离它最近的工人.在文献[9]中,首次关注空间众包任务分配率并提出任务包分配的问题.其中,分配是基于工人和任务之间的一定范围的距离度量,这里的距离使用的是欧几里得距离.文献[10]认为在三维空间中使用欧几里得距离度量方法不够精确,为了提高距离的精确度,Jaya[10]等人提出用半正矢公式测量工人到任务的距离.文献[11] 注意到在某些场合,工人对将要前往的任务地点是否熟悉成为及时正确完成空间任务的关键,因此将最大化位置熟悉度作为优化目标.

目前对以数据质量为主要目标的参与者选择方法的研究还不够深入[12].在优化分配方案时考虑工人完成任务的结果情况是很有必要的.由于请求者的预算有限,又想获得期望的结果,因此目前很多研究都希望在控制成本和达到请求者的预期结果之间达到一个平衡[13].解决这个问题一种比较有效的方法是声誉感知计算[14].在文献[13]中,工人执行一项任务的结果预期质量由工人的声誉和他与该任务地点之间的距离共同决定的,其中工人的信誉还决定了他在每项任务中能得到多少报酬.Wang[15]等人也认为工人完成某项任务的质量受到二者的物理距离和工人的信誉影响,并分别定义了物理位置影响系数和工人的可信度影响系数.

可以发现,目前现有的关于空间众包任务分配的研究大都只把工人的出行距离作为出行成本的单一衡量因素,甚至直接用工人总的行驶路程来表示众包平台的招募成本,并且工人对任务的偏好和声誉这两个因素也没有被充分利用.本文在计算工人的出行成本时,引入了工人对任务地点的熟知度.不仅如此,本文构建的任务分配模型还结合了工人的偏好和声誉,同时兼顾了请求者和工人的利益.

3 相关定义和MPA模型建立

在本节中,首先介绍了一些相关定义,然后引出本文的任务分配问题,即MPA模型的建立.

3.1 相关定义

定义1.工人

用W={w1,w2,…,wm}表示一组工人,单个工人wi={lwi,repi,σi,num},其中lwi表示工人wi的位置,repi代表工人wi的声誉,σi是工人wi可接受的任务的最远距离,num表示工人wi可接受任务的最大数量.

定义2.空间任务

用T={t1,t2,…,tn}表示一组空间任务,单个任务tj={ltj,etj},其中ltj表示任务tj所在的位置,etj是tj的过期时间.

空间众包服务器会定期组织可用的工人,给其分配有效的任务.在本文中,一个任务分配周期内有m个工人,n个任务,一个任务最多由一个工人完成,而一个工人可以完成多个任务.我们假定每个工人有相同的最大任务负载量num,这是由空间众包服务器基于调查评估的[11].我们还假设任务可以在过期之前被完成.

定义3.位置熟悉度

每个工人wi对每个任务tj所在位置的熟悉度定义如下:

(1)

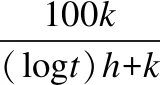
定义4.工人的出行成本

本文用经纬度坐标表示工人和任务的位置信息.用dist(wi,tj)表示工人wi当前位置和任务tj所在位置之间的物理距离,首先,将角度转化成弧度,用到下面的公式:

(2)

则工人wi的经纬度坐标locwi(dlatwi,dlngwi)和任务tj的经纬度坐标loctj(dlattj,dlngtj)分别转化成locwi(rlatwi,rlngwi)和loctj(rlattj,rlngtj).然后,二者之间的距离公式如下:

dist(wi,tj)=

(3)

其中,x=rlatwi-rlattj,y=rlngwi-rlngtj,R是地球半径.

距离越近,对任务所在地越熟悉,工人越能快速顺畅到达,所花费的代价也就越小.因此,本文用一个分数来表示工人执行某一任务的出行成本,如下面公式所示,Tcostij是工人wi执行任务tj的出行成本.

(4)

定义5.工人对任务的偏好

由于需要移动到特定地点才能完成空间任务,因此工人可能想在前往一些目的地的途中执行任务,例如下班回家的路上,或者是偏爱那些距离自己当前位置没那么远的任务地点.我们用prefij表示工人wi对任务tj的偏好:

prefij=1-max[0,min[logσi(dist(wi,tj)),1]]

(5)

由上述公式可知,工人对位于距离阈值之外的任务的偏好度是0,也就是说,工人只可能接受在自己一定距离范围内的任务.

3.2 MPA模型建立

声誉代表了工人成功完成所分配任务的可靠性.声誉值越高,工人成功完成任务的把握就越大.一个工人的声誉值可以从他执行任务的历史数据中推断出来.本文旨在研究以用户体验为导向的空间众包任务分配问题,影响用户体验的3个因素分别是工人到达任务地点的出行成本,工人对任务的偏好以及工人的声誉.可以发现,这3个因素不仅决定了工人执行空间任务的体验感,实际上还关系到工人成功完成所分配任务的可能性.因此本文研究的以用户体验为导向的任务分配问题可以量化为计算工人成功完成任务的概率分数.把工人wi成功完成任务tj的可能性得分记作Probij,计算公式如下:

(6)

然后,建立如下全局目标函数:

(7)

约束为:

(8)

(9)

其中,xij是一个二进制变量,表示任务tj是否分配给工人wi.,每个任务只能分配给一个工人,并且分配给工人的任务数量不能超过他的负载.

综上,本文从用户体验出发,把最大化任务被成功完成的可能性分配问题转化为求最佳全局概率分数问题.

4 MPA模型实现

在一个分配周期内,首先计算m个工人分别针对不同的任务得到的概率分数.如果工人之前没去过将要前往的任务地点,那么出行成本就直接等于二者之间的物理距离.因为通过公式(1),可以发现时间间隔要达到10145.728小时,熟悉度才为1.注意,每个工人都有一个可接受任务的距离范围σ,也就是说当任务所在地距离工人当前位置超过σ时,工人对该任务的偏好为0.计算概率分数的方法如算法1所示.

算法1.计算概率分数

输入：Wloc←worker GPS location

Tloc←worker GPS location

Wrep←worker Reputation

Distance thresholdσ

Time intervalWt

输出：Prob[W][T]

1. for workerwiinWlocdo

2. for tasktjinTlocdo

3.x=rlatwi-rlattj,y=rlngwi-rlngtj

4. Calculatedist(wi,tj) according to formula 3

5. fortijinWtdo

8.prefij=1-max[0,min[logσi(dist(wi,tj)),1]]

9. forwiinWdo

10. fortjinTdo

Prob[i][j]=(prefij×Wrepi)/Tcostij

本文最后的目标是找到使全局概率分数最大的任务分配方案,由于任务分配需要满足一定的约束,这使问题变得困难起来,在这里我们采用一种基于模拟退火算法(Simulated Annealing,SA)的启发式算法.SA借鉴固体的退火原理,在寻找给定函数的全局最优值方面具有一定的优势[18].SA在某一温度下的每次迭代中,都会产生一个新的解,然后通过评估目标函数将新解与当前解进行比较.SA接受更好的解作为当前解,并按Metropolis准则[19]来接受一个比当前解要差的解,这样可以避免陷入局部最优,继续搜索更多可能的解从而得到全局最优解.SA的算法流程如图1所示.

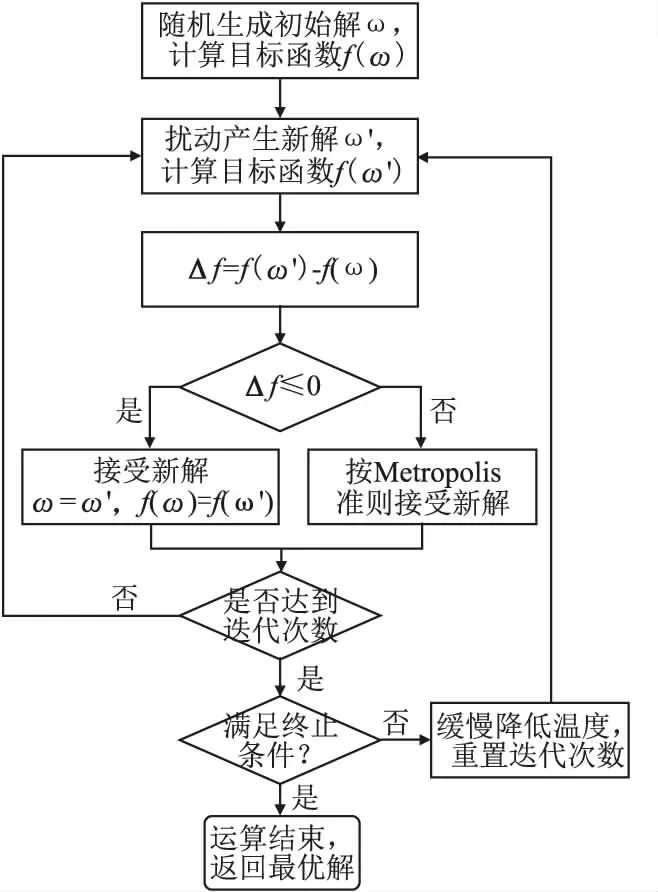
图1 SA算法流程图

可以看出,扰动产生新解的策略对于算法能否快速实现全局收敛非常重要.尤其是当解空间很大时,就要尽可能扩大搜索范围从而防止算法陷入局部最优.传统的模拟退火算法在解决本文这类问题时,通常只采用简单随机交换的方式产生新的解,由于本文的MPA问题搜索空间较大,这种产生新解的方法不能有效地达到预期的结果.为了尽快取得全局最优值,本文设计的MPS-SA在产生新的分配结果时不仅考虑到随机性,还考虑到搜索的方向性,主要采用以下3种方式:

a)在当前的分配结果中任意挑选两个工人,然后随机交换分配给他们的任务,如果其中一个工人没有被分配任务,那么将另一个工人的任务直接转移给他.

b)在当前的分配结果中,任意挑选一个任务tj,然后随机分配给工人wi,如果工人wi已经达到他的最大负载量,不能再接受新的任务,那么就用tj替换掉wi目前执行的概率分数最小的任务,同时将替换掉的任务分配给原来执行tj的工人.

c)在当前的分配结果中,将未形成分配的工人-任务对应的概率分数按从大到小的顺序排列,然后依次对已分配的任务进行重新分配,重新分配的原则是:在这里,假设未形成分配的工人-任务对应的概率分数为pij(表示工人wi如果执行tj,成功的概率分数为pij),其中任务tj已经被分配给了工人wm,而工人wm完成tj的成功可能性分数小于pij,那么就将tj重新分配给工人wi.注意,分配给工人wi的任务数量不能超过他的最大承受数量num.如果超过,不再重新分配,继续查看下一个稍小的概率分数.

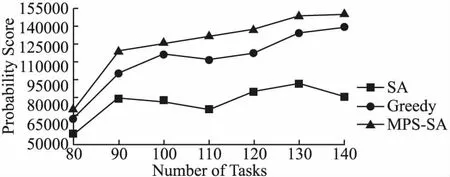
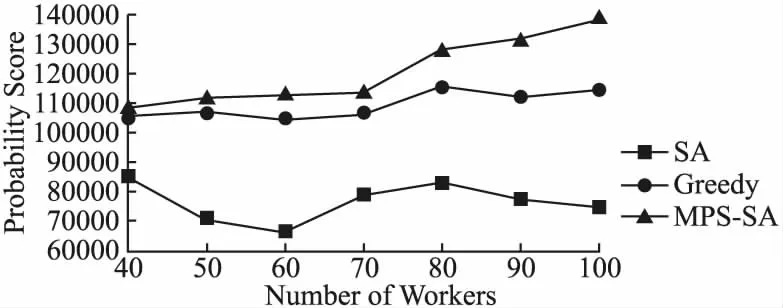
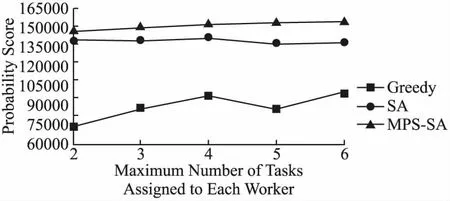
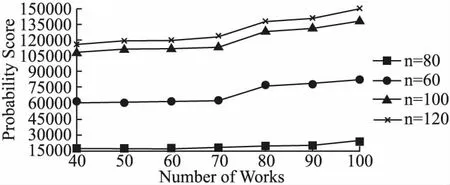
算法2描述了MPS-SA的过程.在某一温度下的每次迭代中,采用上文提到的3种方法产生新解.第7～第11行表示当新的任务分配方案优于当前的任务分配方案时,那么就直接将当前的任务分配方案更新为新的任务分配方案,否则,以一定的概率接受新方案为当前的任务分配方案.在一开始,把当前温度设为最高温度.第8行根据公式(10)更新当前温度,其中ρ是一个常数,表示温度下降的速率.每一温度下的所有迭代结束后,将当前温度Temp与最小的温度Tmin进行比较,当Temp

Temp=ρ×Tmax

(10)

算法2.MPS-SA

输入：Prob[W][T],the maximum temperatureTmax,the minimum temperatureTmin,the rate of temperature declineρ,the iteration timesiter

输出：∑Prob,Set of worker-task pairs

1. Generate the initial task assignment result randomly;

2.Temp=Tmax

3. whileTemp>Tmindo

4. forj=1 toiterdo

5.NewSolution= GenerateNewSolution()

Calculate ∑Probnew

7. if ∑Probnew>∑Probcur

8.CurrentSolution=NewSolution;

9. else Calculate the probabilityp

10. ifp>rand(0,1)

11.CurrentSolution=NewSolution;

12. renew the current temperatureTempby Eq.(10);

5 实验分析

在本节中,我们在真实数据集及仿真数据集上评估了本文提出的MPS-SA算法的性能.首先介绍了数据集和一些实验设置.然后从不同方面对提出的解决MPA问题的算法进行实验分析,给出了不同参数设置下的实验结果,包括不同的任务数,工人数以及工人的最大任务负载量等.

5.1 实验数据集

数据集来自文献[20],其中包含了会员信息数据和项目任务数据,将每个会员都视为一个可用的工人.工人信息数据和任务数据都包含了位置信息,也就是经纬度坐标.对于之前去过的任务地点,工人距离上一次前往的时间间隔在[8,2400]小时内随机生成.另外,为了便于后面的计算,本文的位置熟悉度直接用百分点表示.同样,为了计算方便,用下面的公式标准化工人的声誉值,使其在1～100的范围内.

(11)

由于工人只对地点在自己一定距离范围的任务感兴趣,本文将距离阈值设置为20千米.此外,工人最多能执行的任务数量对实验结果也有影响,在这里将工人的最大任务负载量设置为3个.本文进行50次实验,然后取平均概率分数值(该值量化了工人成功完成任务的可能性,结合本节实际数据,越大越好)作为最后的实验结果.实验运行在一台拥有Intel Core i5-10210U 处理器,8GB RAM的联想笔记本电脑上.操作系统是windows 10,编程语言是Java.

5.2 实验结果

图2表明了在不同任务数量下本文使用的MPS-SA算法和其他算法在性能方面的比较,工人的数量固定在80,其中每个工人最多执行3个任务.由图2可以看出,随着任务数量的不断增加,任务能被成功完成的可能性分数整体呈上升趋势,这是因为所求的概率分数是全局性的.图2清楚地表明本文使用的MPS-SA算法能得到更大的概率分数,这说明我们提出的方法具有一定的搜索最优解的优势.

图2 任务数量对概率分数的影响

不同算法在不同工人数量下的性能对比如图3所示.其中,任务的数量固定在140,每个工人最多执行3个任务.从图3可以看出,对于SA和本文提出的MPS-SA来说,一开始工人数量的变化对概率分数的影响并不是很大,后面随着平台上可用的工人越来越多,目标函数值才增加的较明显.这是因为当工人的规模比较大时,可选的工人范围就大,这样选中更加合适的工人的可能性就越高.除此之外,可以看出本文提出的MPS-SA算法相较于传统的SA算法和贪婪算法在最大化目标函数上仍然是具有优势的.

图3 工人数量对概率分数的影响

图4显示了在工人最多接受的任务数量不同的情况下,概率分数的变化.其中,工人数固定在80,任务数固定在140,每个工人的最大任务负载量分别设置为2,3,4,5,6.图4说明总的概率分数受工人最多能执行的任务数量影响并不是很大.随着工人可承受的任务数量增多,在搜索概率分数较高的工人来执行任务的过程中就不会那么受限,因此用MPA-SA算法求解的最优值在逐步增大.

图4 工人最多执行的任务数量对概率分数的影响

图5显示了在本文提出的算法下,任务能被成功完成的概率分数随不同工人,不同任务数量的变化情况.从图5可以得知,在任务数量固定的情况下,全局最优值随工人数量的增加缓慢增大.当工人数量相同的时候,任务数量越多,概率分数就越大.

图5 工人数量、任务数量对概率分数的影响

6 结束语

本文构建了一个最大化任务成功完成的可能性分配(MPA)模型.为了解决MPA模型中的最大化概率分数问题,本文提出一种有效的基于模拟退火的启发式算法(MPS-SA).MPS-SA算法在每次迭代过程中都致力于找到更优的解而不是盲目地搜寻,这样能尽快得到使概率分数最大的任务分配结果.最后在真实数据集上进行实验,结果表明MPS-SA算法在实现优化分配上具有一定的竞争力.当然,本文还有一些方面需要完善,比如在计算出行成本时,可以根据工人的需求给距离和位置熟知度设置相应的权重.未来,我们还计划考虑空间众包平台的成本预算,另一个可以探究的方向是工人及任务位置数据的动态性.