稀疏表示一致性引导的多视图降维算法

杨在春,魏 巍,2,岳 琴,王 锋,2

1(山西大学 计算机与信息技术学院,太原 030006)

2(山西大学 计算智能与中文信息处理教育部重点实验室,太原 030006)

1 引 言

在现实世界中,通常可以从不同的视角去描述一件事物[1,2],比如一个网页可以由网页文本信息和指向网页的超链接信息来表示;不同的语义可以用不同国家的语言来表示;一张图像可以用不同的视觉特征来描述,如局部二进制模式[3](LBP),位置约束线性编码[4](LLC),定向梯度直方图[5](HOG)等[6].由于多视图数据的每个视图从不同的方面表征同一对象,这些视图共享共同的潜在子空间,因此如何有效挖掘视图之间的关系成为多视图学习的关键.

在图像检索[7]、文本分类[8]、行为识别[9]等许多应用领域中,提取的特征大多位于高维空间,对这些特征的直接操作是比较耗时的.为了解决这一问题,研究者们提出了许多降维方法,通过保留样本的某些性质来寻找合适的低维子空间.主成分分析[10](PCA)、局部保持投影[11](LPP)、稀疏保持投影[12](SPP)等是经典的单视图降维方法.PCA是一种无监督方法,它通过最大化数据的全局方差来获得低维子空间.LPP是一种经典的考虑局部信息的方法,该方法的目标是寻找尽可能保持相邻样本间相关性的最优子空间.SPP是一种经典的稀疏子空间学习的方法,它使降维后的样本保持原始空间中的稀疏表示关系.Gao等人[13]提出一种自适应邻域值选取的LLE算法.这些单视图方法面对多视图数据时,一种简单的方式是将所有的视图拼接起来,但是会急剧增加数据的维数,遭受“维数灾难”问题,而且忽略了视图之间的关系.

典型相关分析[14](CCA)是经典的多视图降维算法,它是最著名的多视图子空间学习方法,其主要思想是将两个视图线性投影到一个潜在的子空间,以最大化视图之间的相关性.但CCA是针对两个视图提出的,不能直接扩展到多视图的情况.Xia等人[15]提出了一种多视图谱嵌入(MSE)方法,该方法针对每个视图构建邻接矩阵,基于保持每个视图上数据的平滑性原则,找到一个公共的低维嵌入.另外,该方法需要预定义图,所以图的质量直接决定了降维的性能,但是如何构建高质量的图是一个开放性问题.针对上述问题,多视图稀疏保持投影[16](MvSPP)被提出.MvSPP是对SPP的扩展,首先基于稀疏表示在每个视图上学习稀疏重构矩阵,然后基于稀疏重构矩阵进行降维,同时使每个视图都与公共子空间保持一致.该方法将稀疏表示和降维过程独立进行,虽然缓解了上述预定义图的困难,但是不能保证稀疏表示挖掘到的信息对于降维过程是最优的.Nie等人[17]提出一种自适应加权图的多视图降维方法,首先为每个视图构造一个拉普拉斯图,然后学习一个与每个视图都近似的公共图,基于学到的图利用一个简单而有效的线性回归函数将数据投影到低维空间.然而该方法依赖最初预定义图的质量.Wang等人[18]提出一种协同正则化多视图稀疏重构嵌入(CMSRE)算法,该方法首先给每个视图学习一个K近邻稀疏图,然后基于学到的图进行降维,同时保持两两视图下样本间的相似性一致.但是稀疏构图与降维过程是分开进行的,不能保证稀疏表示挖掘到的信息对于降维过程是最优的.类似地,Meng等人[19]提出一种相似一致正则化的多视图降维方法,该方法与CMSRE的不同之处在于利用了局部线性嵌入进行构图,Feng等人[20]提出一种局部低秩嵌入的多视图降维算法,该方法采用低秩表示构造近邻图.

此外,还有一些多视图方法基于深度学习展开研究.Andrew等人[21]提出了深度典型相关分析,该方法使不同视图下数据的特征之间线性相关,共同学习两个转换的参数.它可以看作是CCA的非线性扩展.在深度典型相关分析框架和基于重构的方法基础上,Wang等人[22]提出了一种深度典型相关自编码器(DCCAE),它是深度典型相关分析的扩展.DCCAE由两个自编码器组成,同时优化具有典型相关关系的低维特征与自编码器的重构误差.

在上述多视图降维方法中,作者都是将构图与降维作为两个独立的过程,并且基于数据进行一次性构图,在此基础上进行数据降维.显然,这类算法的性能严重依赖于所构图的优劣.为此,本文提出一种稀疏表示一致性引导的多视图降维(Sparse Representation Consensus for Multi-view Dimensionality Reduction,MDR_SRC)算法,该算法通过将基于稀疏表示的构图与基于图的降维整合为一个优化问题,让构图与降维相互指导,从而实现图质量的动态提升,可以有效缓解高维空间一次性构图对基于图降维的不利影响.本文主要贡献概括如下:

1)提出了一种稀疏表示一致性引导的多视图降维算法.该方法通过稀疏表示保持了多视图之间的一致性关系,根据样本对的稀疏表示系数的差异性构图,并基于构建的图进行降维.

2)将基于稀疏表示的构图与基于图的降维整合到同一个优化问题中,实现了二者的相互指导.

3)采用迭代交替策略求解优化问题.在4个公开数据集上的实验结果表明,所提方法的性能优于现有的代表性多视图降维方法.

2 相关工作

2.1 符号描述

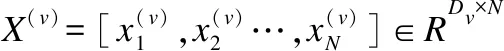
表1 符号表

2.2 稀疏表示

稀疏表示指任意样本可以由除自己外的所有样本的线性组合重构,在重构系数si上加l0范数正则项约束,并且约束重构系数是稀疏的.在线性子空间中,si中的非零元素表示与样本xi在同一子空间的样本对该样本的重构贡献,表达式为:

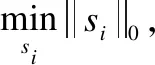
(1)

公式(1)的求解是一个非确定性多项式困难(Nondeterministic Polynomially hard ,NP-hard)问题,一般用l1范数近似l0范数,则可写为:

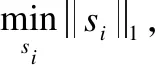
(2)

2.3 多视图谱嵌入

多视图谱嵌入[15](MSE)是一种对多视图的不同特征进行编码以实现有物理意义的谱嵌入方法.它的目标是同时在所有视图上找到一个公共的低维且足够平滑的嵌入,如公式(3)所示:

(3)

其中L(v)是第v个视图的一个非标准化图的拉普拉斯矩阵.它反映了第v个视图中样本之间的邻域关系.α=[α1,α2,…,αV]是一组非负权值,αv反映了视图X(v)在学习获取低维嵌入中所起的重要程度,tr(·)是迹运算.MSE实现了不同视图的低维嵌入在全局上一致.

2.4 协同正则化的多视图稀疏重构嵌入

协同正则化的多视图稀疏重构嵌入[18](CMSRE)是从多视图学习非线性流形的局部稀疏结构,并为其构造有意义的低维表示的方法.首先利用单个视图特征之间的稀疏重建相关性S(v),获得初始的低维表示.然后,利用一个协同正则化方案来更新所有视图的低维表示,目标函数为:

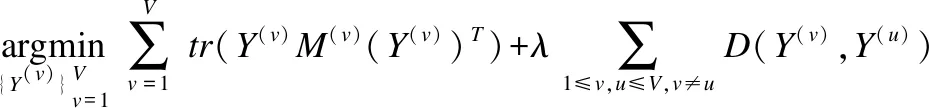
(4)

其中D(Y(v),Y(u))=-tr((Y(v))TY(v)(Y(u))TY(u))表示样本在任意两个不同视图下的相似性保持一致,M(v)=(I-S(v))(I-S(v))T,λ>0为平衡参数.CMSRE在更新每个单一视图的低维表示时,考虑了所有视图稀疏重建的相关性.

3 稀疏表示一致性引导的多视图降维算法

本节具体阐述了所提出的稀疏表示一致性引导的多视图降维模型的构建过程,然后采用迭代交替策略进行求解,算法1描述了整个算法的求解流程.

3.1 模型构建

基于保持多视图下样本稀疏表示一致性的原则,最小化不同视图下样本的公共稀疏表示si在各个视图下的重构损失,对于所有样本,目标函数可以写为:

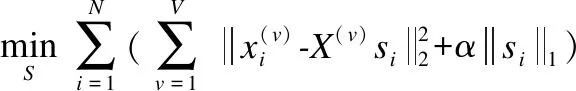
(5)

其中,α为平衡参数,si表示不同视图下所有样本对样本xi的稀疏重构系数,它对自身重构贡献为0,因此sii为0.该目标函数可使得同一个样本在不同视图下的重构系数保持一致.

利用稀疏表示得到的重构系数矩阵指导自适应构图,即如果任意两个样本xi,xj的重构系数si,sj差异大,则说明它们的相似性aij小.并使降维后的数据保持图上的平滑性,若两个样本在图上的相似性大,那么这两个样本的低维表示差异就小,目标函数可写为:

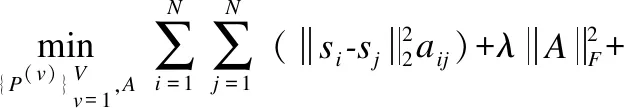
(6)

将稀疏表示挖掘多个视图一致性信息的过程与基于稀疏表示系数构图的多视图降维整合到同一个优化问题中,则可以得到最终目标函数:

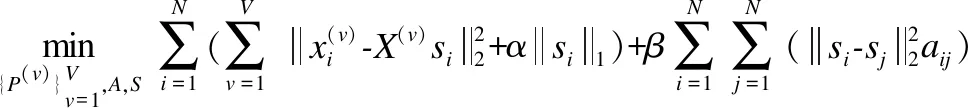
(7)

其中,α,β,γ,λ为平衡参数.该算法利用稀疏重构的思想,通过使不同视图保持一个公共的稀疏表示,保持了视图之间的一致性关系,得到样本在不同视图下的公共重构系数矩阵;然后将稀疏重构系数矩阵用来指导构图,若任意两个样本之间的重构系数差异大,则这两个样本之间的相似性小,得到样本之间的相似性矩阵;最后实现基于图的多视图降维,若任意两个样本在图上的相似性小,则这两个样本的低维表示之间的差异性也小,保持了图上的平滑性.

3.2 模型求解

该模型需要求解的变量有3个,即P,A,S.采用迭代交替优化策略进行求解.

首先,固定P、A,优化S,去掉无关项,则优化目标为:

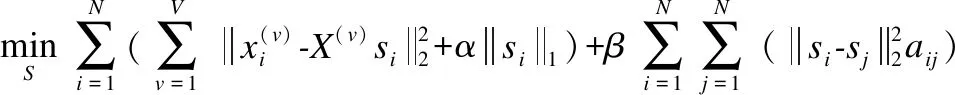
(8)

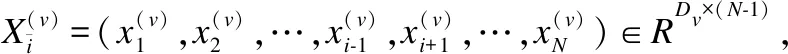
(9)

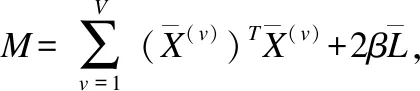
(10)

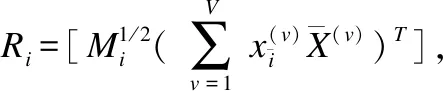
其次,固定P、S,优化A,去掉无关项,则优化问题可写为式(11):

(11)

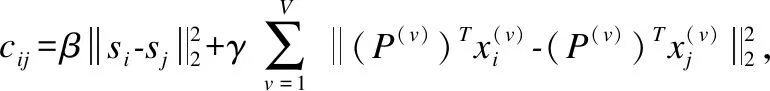
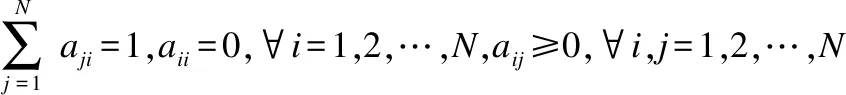
(12)

其中,Vec(·)表示将矩阵列向量依次一个向量接一个向量地组成一个长向量.对矩阵A的每列除了第i个位置进行逐列优化,进而转为凸二次规划问题,用二次规划算法[24]进行求解.

最后,固定A、S,优化P,去掉无关项,则优化问题可写为:

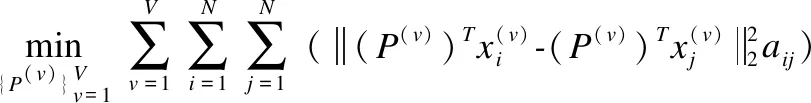
(13)

对于任意的P(v)则有:

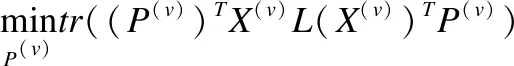
(14)

以上问题可用广义特征值分解方法求解,即:

X(v)L(X(v))TP(v)=φX(v)H(X(v))TP(v)

(15)

对(X(v)L(X(v))T)-1X(v)H(X(v))T特征分解,最终P(v)由最小的dv个特征值对应的特征向量组成.

综上介绍,可以对稀疏表示一致性引导的多视图降维算法进行以下描述,如算法1所示.

算法1.稀疏表示一致性引导的多视图降维算法

输入：X={X(1),X(2),…,X(V)},α,β,λ,γ

输出：Y={Y(1),Y(2),…,Y(V)}

1.初始化S,A

2.while 不满足收敛条件

3. 根据公式(10)更新稀疏重构系数矩阵S;

4. 根据公式(12)更新相似性矩阵A;

5. forv= 1 :V

6. 根据公式(15)更新投影矩阵P(v);

7. end

8.end while

9.forv= 1 :V

10.计算Y(v)=(P(v))TX(v)

11.end

3.3 算法复杂度分析

根据3.2节算法描述可知,所提算法MDR_SRC主要可以分为3步:第1步为初始化S,A(第1行),第2步为迭代更新变量P,A,S(第2～第8行),第3步计算最终的低维数据样本矩阵(第9～第11行).

第1步初始化稀疏重构系数矩阵S,对于S的第i行使用基追踪算法进行求解,基追踪算法可以转化为线性规划问题,以内点法为例,其计算复杂度为O(p(m)),其中p(·)是一个多项式函数.所以初始化稀疏重构系数矩阵S的复杂度为O(Np(m)),其中N为样本数.初始化相似性矩阵A的计算复杂度为O(1),因此第1步的计算复杂度为O(Np(m)+1)≈O(Np(m)).

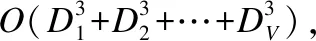
第3步计算低维数据矩阵的计算复杂度为O(NDd),其中Dd=D1d1+D2d2+…+DVdV.

综上所述,算法MDR_SRC的计算复杂度为O(Np(m))+O(T(Np(m)+D3))+O(NDd),最终化简为:O(T(Np(m)+D3))+O(NDd).

4 实 验

为了验证所提方法的有效性,本节系统地与单视图降维方法LPP_BSV、LPP_FC、SPP_BSV、SPP_FC和多视图降维方法MSE、CMSRE、MvL2E在4个公开数据集上进行了比较.

4.1 数据集

实验使用了4个数据集,包括BBC、NUS_WIDE、Caltech101-7和Handwritten,其中BBC为文本数据集,包含从2004～2005年5个主题领域的体育新闻文章对应的BBC体育网站上的544个文档;NUS_WIDE为图像数据集,实验对NUS_WIDE数据集随机取样了615个样本,包含31个类别,用5种不同的视觉特征描述;Caltech101-7是广泛使用的图像数据集,是Caltech101的一个子集,Caltech101包含101个类别,Caltech101-7从中选择了7个广泛使用的类,得到1474张图片,每张图用6种视觉特征来描述;Handwritten为0-9的手写数字图片,每个数字有200幅图片,共2000幅图片,每张图片用6种视觉特征来描述.数据详细信息见表2.

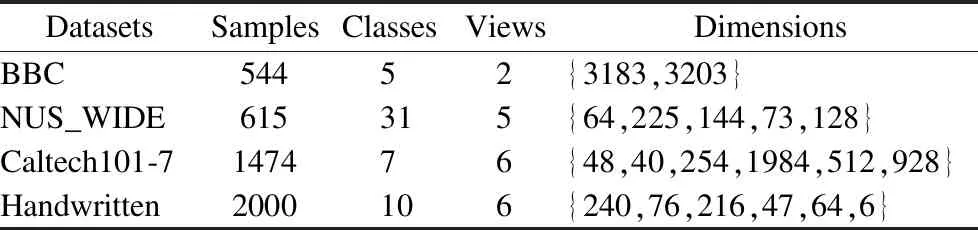
表2 数据集基本信息

4.2 实验设置

实验对比算法包括经典单视图降维算法LPP_BSV、LPP_FC、SPP_BSV、SPP_FC(其中LPP_BSV、LPP_FC分别表示基于单个视图的最优情况和视图拼接的情况,SPP同样)以及多视图算法MSE、CMSRE、MvL2E.

LPP[11]算法思想是原始高维空间中相似的样本点降维后也相似.具体做法是首先构造近邻图,使用KNN方法,这里的参数k取值为20,然后根据所构图指导降维.

SPP[12]利用稀疏表示构造样本间的稀疏重构权值,并将其保留在低维子空间中.具体地,任意样本都可以由所有样本稀疏重构而来,由此可以得到全局稀疏表示,并将这种稀疏关系在降维后得以保持.

MSE[15]算法思想是找一个低维嵌入使得每个视图的分布都是充分光滑的,并且考虑了不同视图在获得最终低维嵌入方面的贡献是不同的,因此,为不同的视图赋予不同的权重,表征该视图在获得低维嵌入的重要程度.该方法使用KNN算法构造邻接图,这里的参数k与LPP算法设置相同,取值为20.

CMSRE[18]算法思想是通过利用多个视图稀疏重构的相关性,从多个视图学习非线性流形的局部稀疏结构,并为它们构造有意义的低维表示.该方法使用KNN算法构造邻接图,这里的参数k与LPP算法设置相同,取值为20.其中的正则项参数λ设置与原文一致,取值范围为{0,0.5,0.6,0.7,0.8,0.9}.

MvL2E[20]算法是通过采用低秩表示,充分利用了多视图特征之间的相关性,从而捕获多个不同视图之间的共同低维嵌入.该方法使用KNN算法构造邻接图,这里的参数k与LPP算法设置相同,取值为20.其中的正则项参数γ设置与原文一致,取值为0.8.

本文所提算法MDR_SRC中的参数α,λ取值范围均为{10-3,10-2,10-1,100,101,102,103},参数β,γ默认取值均为1.根据数据集的规模不同,最终降维维数设置不同的数值.

降维后的数据使用k-means聚类方法进行聚类,聚类个数为真实类别的个数.然后使用聚类精度(Accuracy,ACC)、归一化互信息(Normalized Mutual Information,NMI)和调整兰德指数(Adjusted Rand Index,ARI)作为评价指标.最后分析了所提算法在4个数据集上的参数敏感性.

4.3 实验结果分析

表3～表5展示了所提算法MDR_SRC与7个对比算法在4个数据集BBC、NUS_WIDE、Caltech101-7和Handwritten上的降维结果使用k-means聚类的ACC、NMI和ARI值.

表3 不同算法在4个数据集上的ACC值

表4 不同算法在4个数据集上的NMI值

表5 不同算法在4个数据集上的ARI值

通过分析表3～表5可得知,所提算法在大多数情况下能得到最优结果,可以得到以下具体结论:1)单视图最优的算法LPP_BSV、SPP_BSV在4个数据集上的ACC值、NMI值、ARI值分别优于视图拼接的算法LPP_FC、SPP_FC,这是由于直接拼接视图可能会失去多视图数据原本的物理意义,拼接也会导致数据维数变高,降维性能下降;2)多视图降维算法MSE、CMSRE、MDR_SRC在4个数据集上的ACC值、NMI值、ARI值均优于单视图最优算法LPP_BSV、SPP_BSV,这是由于多视图降维算法考虑了视图之间的关系,将多视图数据之间的信息进行了很好地融合;3)所提算法MDR_SRC在4个数据集上的ACC值、NMI值、ARI值相比其它多视图降维算法MSE、CMSRE、MvL2E在大多数情况取得最优结果,这是由于MSE算法需要预定义图,降维的性能依赖图的质量,CMSRE算法将稀疏表示和降维过程独立进行,不能保证稀疏表示挖掘到的信息对于降维过程是最优的,MvL2E算法将低秩表示和降维过程独立进行,低秩表示挖掘到的信息没有充分利用到降维过程中.而所提算法MDR_SRC通过稀疏表示保持了多视图之间的一致性,根据样本对稀疏表示系数的差异指导构图,再根据图指导降维,将基于稀疏表示的构图与基于图的降维过程统一到一个优化问题中,实现了二者的相互指导.

4.4 参数敏感性分析

对所提算法MDR_SRC在4个数据集上不同参数下的ACC、NMI、ARI值进行了可视化展示,分析了参数敏感性,所得实验结果如图1～图3所示,可以看出所提算法可以在较小的范围内搜索到最优值.分析图1、图2可以得知,所提算法MDR_SRC的聚类ACC、NMI指标在Caltech101-7数据集、Handwritten数据集上对参数α,λ不太敏感,在NUS_WIDE数据集、BBC数据集上对参数α,λ比较敏感,并且往往是在同一个λ且不同的α情况下该算法的聚类ACC值、NMI值比较敏感.分析图3可以得知,所提算法MDR_SRC的聚类ARI指标在Handwritten数据集、NUS_WIDE数据集上对参数α,λ不太敏感,在BBC数据集、Caltech101-7数据集上对参数α,λ比较敏感,同样也是在同一个λ且不同的α情况下该算法的聚类ARI值比较敏感.这是由于BBC数据集是分类型文本数据集,因此所提算法对参数比较敏感.

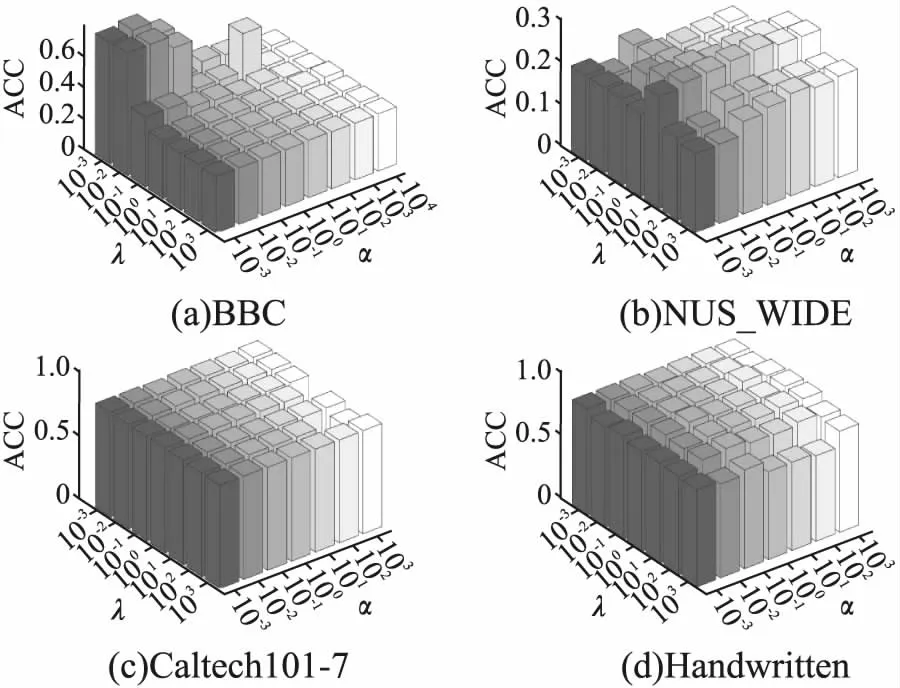
图1 所提方法在不同参数下的ACC值

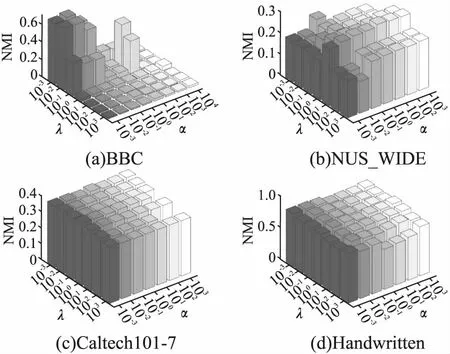
图2 所提方法在不同参数下的NMI值

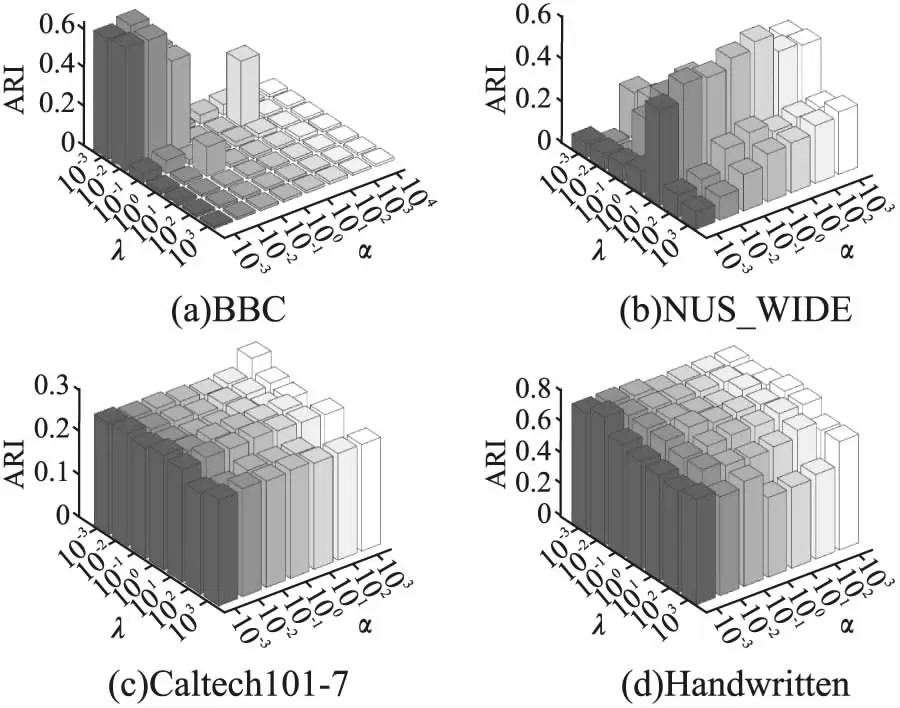
图3 所提方法在不同参数下的ARI值

5 结束语

本文提出了一种稀疏表示一致性引导的多视图降维算法.该算法利用样本对稀疏表示系数的差异指导构图,根据构建的图指导降维,降维后样本之间能够保持图上的平滑性;将基于稀疏表示的构图与基于图的降维整合为一个优化问题,实现了构图与降维的相互指导,缓解了预定义图影响降维算法性能的问题.实验分析验证了所提算法的性能优于现有的代表性多视图降维方法.然而,在许多实际应用中可能存在视图缺失的数据,因此如何把稀疏表示一致性的思想扩展到不完备多视图降维背景下将是一个值得研究的问题.