基于多策略融合的灰狼算法的多阈值图像分割

李斐朱晓磊

(1. 山东建筑大学信息与电气工程学院，山东 济南 250101；2. 山东建筑大学山东省智能建筑技术重点实验室，山东 济南 250101；3. 积成电子股份有限公司，山东 济南 250100)

0 引言

图像分割是指根据目标与背景的先验知识，将图像划分为某些特性上相近的连通区域的集合，通常为模式识别、图像理解、图像压缩等应用的基础准备，是从图像处理到图像分析的关键步骤[1]。 目前，自动化的图像分割主要基于边缘和区域的方法。由于每种方法具有不同特点，故适用于不同类型的图像。 其中，基于图像灰度的阈值分割方法属于后者，是一种最为简单有效的分割方法，根据图像灰度的相似性，直接得到划分好的区域。 阈值分割的前提是图像中要提取的目标物与其背景在灰度特性存在差异，具有了不同的灰度值区域。 图像的阈值个数由具体的划分程度要求决定，单域值可以简单地将图像划分为两个区域，当实际应用中需要将图像划分为多个目标区域时，需要多个分割阈值。 传统的阈值分割算法，通过穷举法遍历所有灰度值寻找最优阈值，其耗时较长，特别是当利用阈值分割算法进行多阈值分割时，计算法复杂度随阈值个数呈指数级增长，因此需要更加高效和智能的阈值寻找方法。

元启发式算法于20 世纪60 年代提出，利用仿生学原理，模拟生物或自然现象中群体移动和定位的行为机制进行目标函数优化，具有计算量低、优化效率高和自我调节等优点，已在解决非确定性多项式困难(Nondeterministic Polynomial－hard，NPH)、组合优化等问题上取得广泛的应用。 元启发式算法也已用于图像的多阈值选择问题上。 阈值处理可视为一种统计决策问题，常用的统计鉴别分析中的测度有最大类间方差和信息熵，吕鑫等[2]结合鸟群算法中飞行行为的思想优化麻雀搜索算法，提出改进麻雀搜索算法(Improved Sparrow Search Algorithm，ISSA)，提高算法的搜索能力和开拓能力，获得更好的全局最优值，同时将最大类间方差和Kapur 熵作为ISSA 的目标函数进行图像的多阈值寻优，得到更加稳定高效的分割性能；常君杰等[3]在乌鸦算法中引入Levy 飞行机制，提高全局搜索能力，并采用自适应尺度调整系数限制Levy 飞行的搜索范围，加快寻优速度，改善了二维Tsallis 熵多阈值图像分割计算量大的问题；贾鹤鸣等[4]采用Kent 混沌映射初始化萤火虫算法，并利用改进后的优化算法优化了二维Renyi 熵函数中的变量，分割了复杂环境中的污油图像，提高了图像分割的准确度；霍星等[5]提出一种新的天牛须算法(Antennae Search Algorithm，BAS)进行二维K 熵下图像的多阈值分割，将原始BAS 算法拓展为二进制离散形式并将其作为辅助算法与BAS 结合，解决了BAS 易陷入局部最优的不足。 基于二维灰度直方图的方法比基于一维灰度直方图的方法计算更加复杂。 灰狼算法(Grey Wolf Optimizer，GWO)是MIRJALILI 等[6]提出的一种新型元启发式算法，其算法简单、参数少、易实现，具有良好的搜索和开发能力，已广泛应用在工程调度[7]、频谱分配[8]、图像分割等领域。 刘磊等[9]提出一种改进的灰狼算法(Improved Grey Wolf Optimizer，IGWO)，在搜索过程引入莱维飞行机制，避免陷入局部极值；动态调整收敛因子和随机权重以提高搜索精度，在Otsu 测度下取得了优秀的图像多阈值分割结果，在这一算法中，灰狼的社会等级划分是固定不变的，一定程度上限制了算法的收敛性能。

综上所述，层出不穷的元启发式算法在处理图像多阈值分割问题上各有优势，并且在有效改进策略下优化性能显著提升。 为充分利用灰狼算法良好的搜索能力并进一步提升算法的收敛速度和计算精度，文章提出融合多种策略的灰狼算法(Grey Wolf Optimizer Fused With Multiple Strategies，MSGWO)，对复杂图像和多目标图像开展了Renyi 熵多阈值分割；提出动态搜索策略，动态调整迭代初期和后期的头狼等级划分方式，对个体位置更新范围进行前期扩展和后期压缩，加快寻优速度，克服迭代后期易陷于局部极值的缺陷。 采用所提算法与其他几种元启发式算法进行标准图像的多阈值分割实验，通过对比迭代曲线、峰值信噪比和特征相似度，证明所提算法的优势。

1 Renyi 熵

Renyi 熵是香农熵的推广，在香农熵基础上引入阶参数α，对信息的度量更加灵活和具有一般性[10]。 假设N个离散随机变量X具有概率分布{pk}，k为随机变量编号，k＝1，2，…，N，其α阶Renyi 熵形式由式(1)表示为

基于Renyi 熵的多阈值图像分割原理为:假设大小为m×n的灰度图像记为f(x，y)(1≤x≤m，1≤y≤n)，其灰度级数为L，希望将图像分割为K个目标区域，则需要选取D＝K－1 个阈值t1，t2，…，tK－1。此时图像的Renyi 熵由式(2)表示为

熵衡量了系统的不确定性或平均信息量，阈值分割希望每个分割后的区域内部的灰度是相近的，目标和背景的信息量最大，因此阈值分割的目标函数为最大化各个区域的Renyi 熵，由式(3)表示为

2 策略融合的灰狼优化算法

2.1 灰狼算法

灰狼算法(GWO)是一种新型的元启发式智能优化算法，通过模拟灰狼的社会阶层结构和狩猎行为从而寻找适应函数的最优解。 根据分配任务的不同，将个体分成头狼、探狼、猛狼，个体间互相协助、共享信息、协同完成觅食任务。 狼群算法通过对当前群体施加游走、奔袭、围攻3 种智能行为捕获猎物，从而使群体进化到接近最优解的状态。 GWO 算法具有良好的广度开拓和深度开采能力且算法设计简单，其初始参数较少、收敛速度较快。

狼群的社会等级分为4 级。 狩猎过程中，离猎物最近的3 只狼记为α、β和δ狼，其社会地位最高，其他狼群则记为ω狼，在α、β和δ狼的引领下更新自己的位置。 狼的社会地位并非一成不变，每次位置更新后，狼群将进行一次优胜劣汰，α、β和δ狼随之更新为当前3 个最优的解，其他候选解ω狼不断向群体中的3 个最优解移动。 算法的数学模型描述如下:

追踪猎物过程，首先计算当前灰狼与α、β和δ狼之间的距离和，由式(8)表示为

ω狼的位置更新由式(9)表示为

最终ω狼个体移动后的新位置由式(10)表示为

2.2 非线性收敛因子

如式(6)所示的a是收敛因子，按照迭代次数线性递减，该因子决定了个体更新的幅度。 而线性变化的振幅并不能很好地适应寻优过程，可能导致收敛速度较慢。 分析迭代过程，在初期的随机分布位置下，大部分个体距离最优点可能较远，需要更大的步长以便快速靠拢最优位置，在迭代后期，距离最优位置已经比较接近，更小的更新幅度适合局部精细查找，避免出现最优位置附近的震荡，从而加速收敛、提高算法精度。 为此，文章提出一种变化幅度由大到小的非线性振幅调节因子，由式(11)表示为

式中t为当前迭代次数；M为最大迭代上限。

2.3 自适应探索策略

灰狼算法将狼群分为α、β、δ和ω等4 个等级，每次迭代中α、β、δ狼对应前3 个最优解，引领种群中其他个体ω进化。 文献[11]提出了3 个等级的改进灰狼算法，将狼群的最低2 个等级合并为一组，以降低计算复杂度，加快收敛。 在新型元启发算法黑猩猩算法[12]中，个体的更新步骤与灰狼算法类似，不同的是个体的位置更新是同时向驱赶者、拦截者、追逐者和狩猎者4 类黑猩猩的当前位置靠拢。在此启发下，文章提出一种自适应探索策略，改进灰狼算法。

纵观整个迭代过程，虽然在求解过程中事先并不知道最优解的位置，但随着狼群开发和探索，种群的位置是逐步向最优解的位置靠拢的，种群的更新也是逐步细化的。 始终选取α、β、δ3 个最优解位置作为更新方向，并不适应从粗到细的更新变化，因此文章考虑采用动态探索策略，在迭代的初期和末期，采用不同的等级划分方法。 初期阶段，狼群距离最优解位置可能较远，即便跟随3 个最优解进行位置更新，个体也是从大方向上向猎物靠拢，此阶段所有个体均距离猎物较远，可以将4 个最优解记为γ狼，与α、β、δ狼共同带领其他个体进行位置更新，个体位置更新的落点由3 个最优解包围的范围扩展到4个最优解包围的范围，加大了前期搜索的范围。 经过多轮迭代后，狼群已经发现猎物并聚集在其附近，此时狼群与猎物之间的距离比较近，适当收缩更新位置落点范围，以便个体进行精细位置更新，减少计算复杂度，在迭代后期，将带领等级减小到两个，即只保留α、β狼2 个高级等级，其他狼均划为ω狼等级。

自适应探索过程的狼群位置更新过程如下，首先引入距离猎物最近的排名第4 的个体记为γ狼，社会等级位于ω狼之上，计算个体与其之间的距离，并以γ狼为引导，个体向其靠拢，由式(12)和(13)表示为

式中t为当前迭代次数；为第i个个体的更新位置；d(t) 为当前最优解位置与上次迭代的最优解的欧氏距离；和分别为解空间的上、下限。用最优解距离变化为标准，当变化大于空间最大距离的0.01 时，说明该个体距离猎物还较远，取距离猎物最近的前4 个最优解为引领，扩大了其他个体的位置落点范围；反之，说明该个体距离猎物较近，取距离猎物最近的前两个最优解为引领，其他个体均作为ω狼，在收缩的较小落点范围内进行精细更新。

2.4 柯西变异

为了避免在寻优的过程中个体陷入局部极值的问题，在迭代过程中引入个体的柯西变异机制，增大狼群对全局的探索能力。 标准柯西分布比标准高斯分布更加矮宽，具有更大的拖尾，因此容易产生更大的扰动能力，个体按照柯西分布随机产生较大扰动，变异公式由式(15)表示为

3 策略融合的灰狼算法多阈值图像分割流程

利用Renyi 熵最大化作为图像分割的目标函数，优化算法通常以寻找最小值为优化目标，因此取Renyi 熵的负值为优化的适应度函数。 多策略融合灰狼算法下的多阈值图像分割流程图如图1所示。

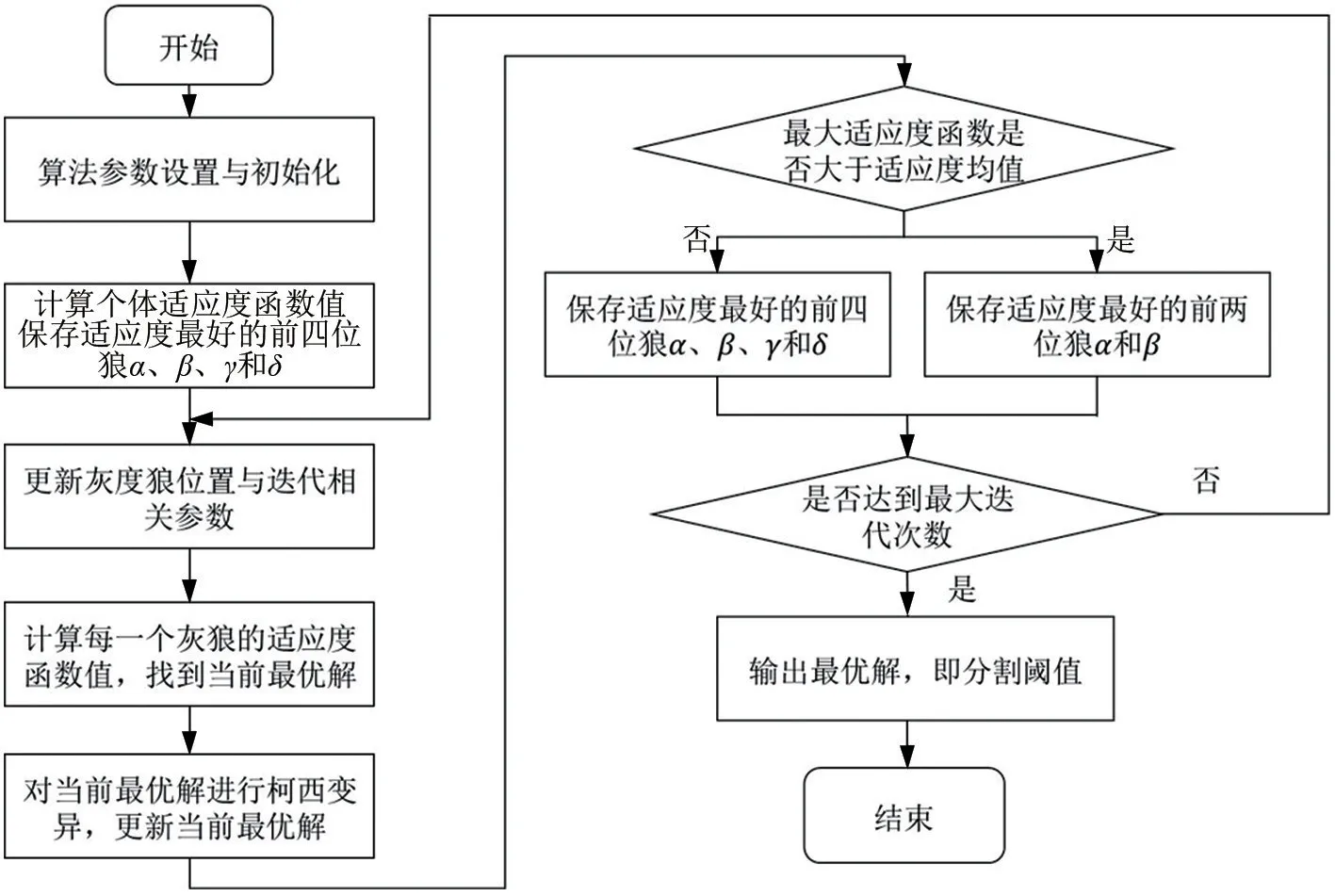
图1 多策略融合灰狼算法下的多阈值图像分割流程图

4 实验结果与分析

为验证文章提出的多阈值分割算法的有效性，选取灰度级为256 的标准测试图像Lena、cameraman和peppers 作为多目标分割对象，进行不同阈值数量下的分割。 同时，为了说明融合策略灰狼优化算法的寻优效果，选取原始灰狼算法、正弦余弦算法(Sine Cosine Algorithm，SCA)[13]、 蜻蜓算法(Dragonfly Algorithm，DA)[14]、以及新型元启发式算法的改进——麻雀搜索算法(ISSA)[2]和改进灰狼优化算法(IGWO)[9]作为对比。

设置所有的优化算法种群数为20，最大迭代次数为200，个体每个维度的取值范围为[0，255]。 所有算法的初始化时随机生成，实验结果取重复20 次实验的均值。 衡量分割的指标采用峰值信噪比(Peak Signal－to－Noise Ratio，PSNR)，记作P。 通常，P值越大，图像的分割效果越好。 计算公式由式(16)表示为

式中f(i，j) 为原始图像；g(i，j) 为分割图像；m和n分别为图像的长和宽。

此外，特征相似性(Feature Similarity，FSIM)，记作F，也是衡量图像分割效果的有效指标，通过相位一致(Phase Congruency，PC) 特征和梯度幅度(Gradient Magnitude，GM)的耦合评估原始图像与分割图像的相似度，计算公式由式(17)表示为

式中Ω 为整个图像空间；x为二维图像中的像素坐标；SL(x) 为相位一致特征与梯度幅度在x处的融合相似度；PCm(x) 为原始图像与分割图像的在x处的相位一致特征的最大值，关于该指标的具体描述可见参考文献[15]；F取值在[0，1]，越接近1，图像越相似。

4.1 MSGWO 算法的有效性

为说明多策略融合灰狼算法改进的有效性，考查每种改进单独作用与原始灰狼算法以及MSGWO的迭代过程对比。 以Lena 图像的3 阈值分割为例，其迭代曲线如图2 所示。

图2 GWO 改进方法效果对比图

由图2 可见，每一种改进方式单独作用在GWO时，几乎都会产生更加低的适应度函数值，除了自适应搜索方法在迭代次数30 附近有个别位置逊于原始GWO，但是后续该曲线迅速收敛到GWO 对应的黑色实线之下。 整体上看，3 种改进策略的MSGWO表现最佳，收敛速度最快且精度也最高，说明改进策略的有效性。

4.2 多阈值分割效果

选取不同阈值个数，采用MSGWO 对3 幅标准图像的分割结果如图3 所示。

图3 文章算法对Lena、cameraman 和peppers 的不同阈值下的分割结果图

第一列图像为原始图像，第2 到5 列是阈值个数分别为2、3、5 和6 等4 种情况的分割图像。 其分割结果直观地反映了随着阈值的增加，图像细节越丰富，则信息越完整，由此也看出多阈值分割的必要性。

4.3 迭代过程对比

为观察算法的精度和收敛性，对比文章算法与其他元启发式算法的迭代过程。 选取3 幅标准图像进行6 阈值的分割，以最小化负的Renyi 熵为优化目标，迭代过程曲线如图4 所示。

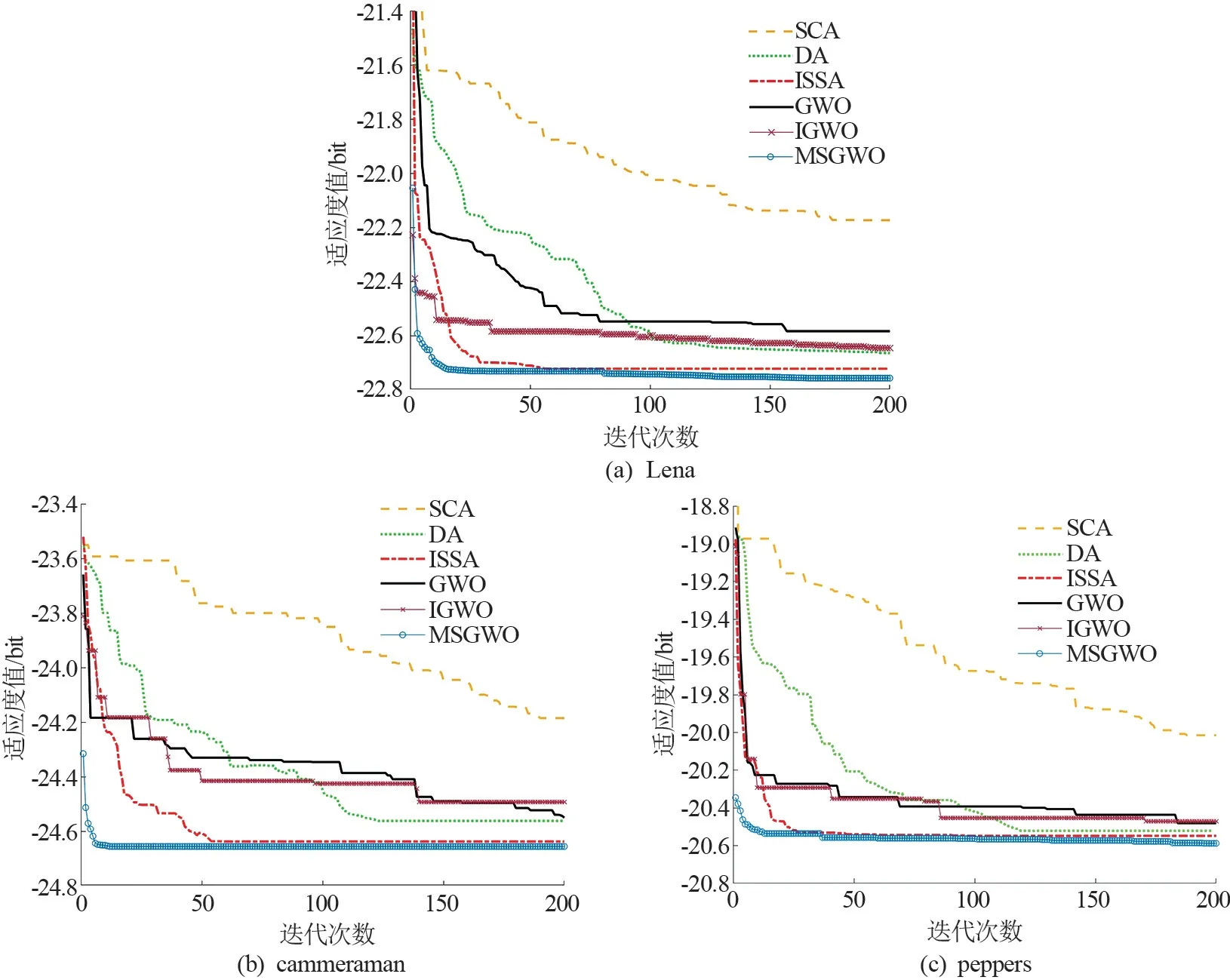
图4 迭代过程曲线图

观察3 幅曲线图，从迭代过程上看，改进后的优化算法普遍比原始优化算法的收敛性好。 从迭代结果可知，改进算法的精度也普遍优于原始算法，其中DA 算法的精度有时优于部分改进算法，但整体收敛较慢； MSGWO 和ISSA 为精度最好的两个算法，而MSGWO 相比于ISSA 的优势在于其快速的收敛性，这一点在迭代初期表现很明显，MSGWO 的曲线明显地处于最低位置。 以Lena 图像为例，ISSA 的迭代曲线收敛也很迅速，在迭代60 次后达到－22.72 bit的最小适应度值，而收敛到相同适应度值，MSGWO 仅需迭代15 次，迭代次数节省75%；cameraman 图像中，ISSA 迭代49 次收敛到最小适应度值－24.65 bit，MSGWO 仅用10 次，迭代次数节省82.1%；peppers 图片中，ISSA56 次收敛到最小适应度值－20.56 bit，MSGWO 仅用36 次，迭代次数节省35.7%；迭代次数平均可减少64.3%。 因此，MSGWO是收敛速度快且精度高的多阈值求解方法。

4.4 分割指标对比

为更加客观地对比几种元启发式算法在多阈值图像分割上的性能，将4.3 节中精度较高的3 种算法——ISSA、IGWO、GWO 和所提算法MSGWO 进行峰值信噪比和特征相似性指标的对比，分别用3 和6 阈值对3 幅标准图像多阈值分割，两项指标的统计见表1。

表1 峰值信噪比和特征相似性指标统计表

观察表中数据，峰值信噪比和特征相似性指标并非完全分布一致，因为峰值信噪比单纯计算图像灰度值差异，而特征相似性结合相位一致性和梯度的特征，可以描述图像中的感兴趣区域，往往认为其是比峰值信噪比更好的图像相似性评价指标，MSGWO 可以取得至少一个指标下的最高分，不失为一种稳定优质的多阈值分割方法。

5 结论

通过上述研究可知:

(1) 通过消融实验，在灰狼算法上单独实施了3 种改进措施，即非线性收敛因子、自适应搜索机制和柯西变异。 其均提高了灰狼算法的收敛性和精度，3 种改进策略融合可以实现优势叠加，得到更高的收敛性和精度。 表明文章提出对灰狼算法的3 种融合改进策略可以有效提高收敛性和精度。

(2) 多阈值分割对比了MSGWO 与其他新型元启发式算法。 从分割结果上看，MSGWO 可取得峰值信噪比和特征相似性中至少一项指标的最高分，分割精度高。 从分割过程看，MSGWO 具有更加快速的收敛性，达到与次优算法相同的最小收敛值，MSGWO 的迭代次数平均可节省64.3%。