基于传统图像处理联合深度学习的FPCB 自动缺陷检测算法

张 鲲， 邓明星

（武汉科技大学汽车与交通工程学院， 武汉 430065）

0 引 言

FPCB 作为现在电子产品中不可或缺的电子零部件，其质量的检测在整个工艺过程中具有非常重要的地位。 深度学习是近年来比较新型有效的一种算法，被大量地运用到了缺陷检测领域。 葛路等学者［1］探讨了深度学习模型在工业产品表面缺陷检测领域的应用。 研究是以Cp 工业产品缺陷检测为着眼点，在设计检测方案时应用深度学习模型并辅助图像处理等相关技术，通过实验分析得到最佳应用模型。 潘甜等学者［2］提出了基于深度学习的飞机蒙皮缺陷检测的方法，能快速定位飞机蒙皮表面会出现裂纹、撞击和腐蚀的问题。 田浩杰等学者［3］提出了基于深度学习来实现线圈炮缺陷的自动检测与分类，采用双边滤波算法进行样本图像增强，降低噪声对成像的影响，并基于单样本几何变换的数据增强策略扩充样本数量，提高模型的适应性。 张浩等学者［4］提出了一种基于深度学习在海缆表面缺陷检测的系统，为了减小模型的复杂程度，采用了RPN Loss＋Fast RCNN Loss 的联合训练方法。 杨凯等学者提出了一种基于深度学习的缺陷检测模型，该方法主要通过改进的VGG16 模型进行缺陷识别。 陈宗仁等学者［5］提出一种基于深度学习的金属机械零件表面缺陷检测方法，采用中值滤波方法对金属机械零件图像中的脉冲噪声进行检测和滤波处理，然后再引入深度学习算法。 针对车载导航导光板表面缺陷像素值分布不均且普遍较小、背景复杂多变等特点，王昊等学者［6］提出了基于改进掩膜区域卷积神经网络模型检测车载导航导光板。 刘瑞珍等学者［7］提出了一种基于深度学习的偏光片缺陷实时检测算法，设计了一个新的并行模块用于构建偏光片缺陷检测网络，模块将不同尺寸大小的卷积核相混合，与传统的卷积层相比，可以融合不同尺度的特征并能提取到更丰富的缺陷特征。 王鸣霄等学者［8］提出了一种基于两级分层深度卷积神经网络的排水道缺陷自动识别与分类系统。 施恺杰等学者［9］提出了一种低成本、高效率的缺陷检测方法，设计了一种两段式的网络结构，第一部分是从原始图像的各层特征图中逐像素地学习特征来完成分割，第二部分则是将分割后的图像进行整合后判断是否存在裂缝。 针对铸件X 射线图像获取困难、人工及传统方法效率低且漏判率高的问题，于宏全等学者［10］提出了一种基于深度学习的铸件缺陷检测方法。 上述的方法，用了很多的神经网络训练和搭建技巧去提升网络检测的准确率，但是没有从根本上解决网络缺陷图片数量不够，导致准确率难以提升的问题。 本文提出了利用传统图像处理方法对图像进行预处理增强图像质量和图片多样性，并结合优化深度学习的方法，设计出了一种完全可以满足实际检测PFCB 需求的自动检测算法。

1 缺陷数据集划分

深度学习的方法要应用到缺陷识别的领域必不可少的一项因素是缺陷数据集，所以在进行算法研究前，首先在FPCB 厂家进行了数据采集，并对数据进行了划分。

研究采集了FPCB 在生产过程中可能出现的6种缺陷，如图1 所示。 由图1 可知，6 种缺陷分别包括：黑色异物、凸起、缺口、开路、短路、白色异物，这些缺陷图的分辨率都是100×100 的灰色图像。

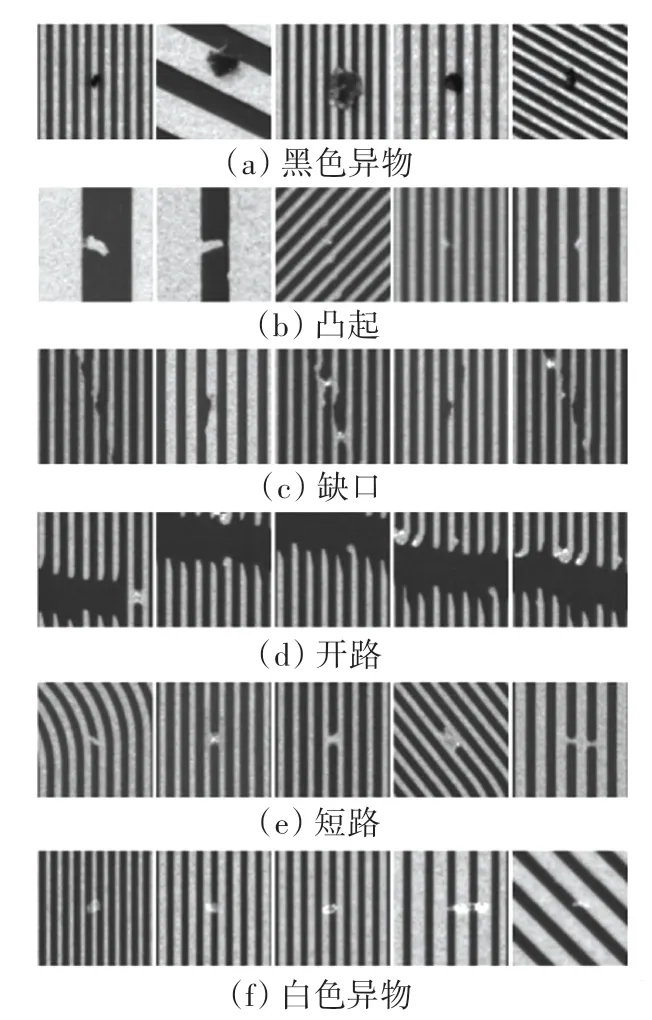
图1 FPCB 缺陷图Fig. 1 FPCB defect map

6 种缺陷图的数量如图2 所示。 由图2 可以发现，每种缺陷图的数量都较少并且分布得不均匀，把采集到的缺陷图像以7 ∶3 的比例按类别随机分为训练集和验证集。

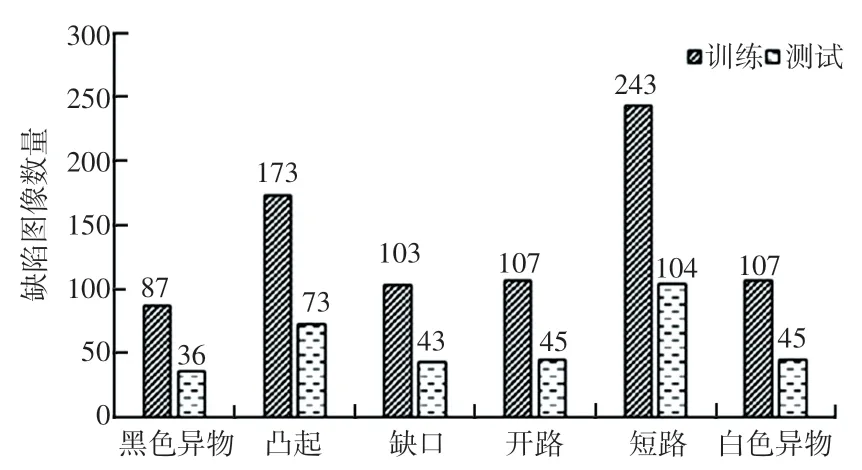
图2 缺陷图像数量Fig. 2 Number of defective images

2 数据预处理

在把数据送入神经网络训练之前还会进行预处理的操作，数据预处理可以有数据增强的效果，并在现有基础上提高网络的准确率。

图像预处理的3 种主要方法如图3 所示，分别包括：图像滤波、灰度变换和图像转换。

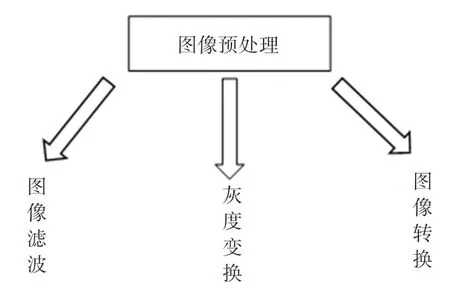
图3 图像预处理方法Fig. 3 Image preprocessing method

2.1 图像滤波

图像滤波也可以称为图像平滑处理，其操作对象为灰度图像。 根据图像中噪声类型和分布情况，可以选择将图像滤波的方法搭配使用以完成对图像的去噪处理。 图像滤波的原理就是选择合适的滤波器在图像窗口上移动，利用设计的滤波器中窗口函数与图像窗口建立某种数学关系以达到去除噪声的目的，目前常用的滤波器有线性滤波、非线性滤波和卷积核滤波，对应过来就是图像的均值滤波、中值滤波和高斯滤波等。 其中，均值滤波法在削弱随机噪声上效果突出，但是会使图像变得模糊，因为在进行噪声滤除时，对于图像的边缘也是同样处理，这就会造成图像中本来明显的边缘变得模糊。 均值滤波的公式具体如下：

中值滤波使用的是非线性滤波器来对图像进行平滑，将其与均值滤波做对比，可以发现中值滤波处理后的图像不仅留存了一些小的细节部分，而且噪声也明显减弱。 中值就是把给定的变量按从小到大的顺序进行排列，排列之后取中间变量值、即中值。对应来看，中值滤波可理解为，设计一个结构元素在图像上滑动，并将元素内像素灰度值升降排序后的中值设置为此元素的中心灰度值。 例如，假设有一个3×3 的窗口，其窗口内的像素灰度值从小到大为g1，g2，g3，g4，g5，g6，g7，g8，g9，则窗口中心灰度值可表示为：

高斯滤波同均值滤波有个相同点，都是使用线性滤波器，可以去除图像高斯噪声（噪声的概率密度分布函数服从正态分布）。 高斯滤波需要先寻找高斯掩膜、并根据高斯分布，然后再对掩膜内像素点通过卷积完成相加，此时得到的值就是窗口的中心值，最后对图像中的像素点重复进行该过程。 高斯模板的计算方式可用如下公式来描述：

其中，σ决定高斯函数宽度，假设当σ＝0.8 时，高斯滤波核的计算为：

而高斯滤波窗口中心处像素值可表示为：

在本系统实验中，对比使用了上述各滤波方式，根据滤波图像后续的处理情况，结合均值和中值两种滤波方式来对缺陷图像进行组合滤波，最后表现出不错的去噪效果。 滤波前后图像效果对比图如图4 所示。

图4 滤波前后对比图Fig. 4 Comparison before and after filtering

2.2 灰度变换

灰度变换针对图像中的像素点来进行运算。 在采集图像时，由于环境因素的影响，最后摄取的图像呈现出对比度不够或亮暗影调的比率较小（动态范围）的效果。 针对这一问题，使用灰度变换的方法可以很好地改善图像效果，此方法就是设计一个变换函数来改变输入图像的灰度值。 使用合适的灰度变换方法不仅能对图像进行增强，而且目标区域的特征会变得凸显。 常用的灰度变换关系为线性变换。 灰度变换是通过某变换关系来达到改变图像灰度值的目的，数学表达式可理解为：

假设有输入图像f（x，y），线性变换后的输出图像g（x，y），两图像的灰度范围分别为［a，b］，［c，d］，其为线性关系，用数学公式可表示为：

根据k的取值大小，有如下几种情况：

（1）当k ＞1 时，会使图像灰度取值的变化范围变大，也就是图像对比度的增大，使用此方法可以改善曝光不足的情况。

（2） 当k＝1 时，不改变图像整体的灰度取值变化范围，但是灰度取值区间会随a和c的大小而上下平移，其结果就是使整个图像更暗或更亮。

（3） 当0＜k ＜1 时，变换输出后图像灰度取值范围会变小，图像对比度变小。

（4）当k ＜0 时，相当于把图像的灰度值进行反转，结果就是图像中亮的变暗，暗的变亮。

本方法中对摄取的缺陷图像使用了灰度线性变换算法以改善图像，质量方便后续的处理。 使用此方法达到增强对比度的效果，处理前后的对比效果如图5 所示。

图5 灰度变换前后对比图Fig. 5 Comparison diagram before and after grayscale transformation

2.3 图像转换

图像转换包括图像缩放、翻转和拉长。 转换的参数如缩放比例、翻转角度、拉长长度，这些参数在每次训练时都是随机的。 因此，能够显著增强了数据的多样性，并有效地避免了网络训练的过程中出现过拟合。

3 卷积神经网络架构搭建

3.1 卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN）是一类包含卷积计算且具有深度结构的前馈神经网络，可以有效实现端到端的特征提取，是图像识别的常用模型之一。 在卷积神经网络的发展历程中，出现过许多经典的网络结构，这些经典CNN 网络的研发都曾极大地促进了领域的发展。 LeCun 等学者［11］在1998 年提出的LeNet 模型是CNN 的开篇之作，对神经网络的发展有着重要意义，但当时并未受到广泛关注。 2017 年，Krizhevsky 等学者［12］提出的AlexNet 模型具有更深的网络结构，成为了当年ImageNet 图像识别竞赛的冠军，可以说AlexNet的出现使得已经沉寂多年的深度学习领域开启了黄金时代。 随后，在ImageNet 竞赛中不断涌现出经典的网络模型。 Visual Geometry Group 提出的VGG 系列模型［13］，在AlexNet 的基础上构建了更深的网络结构，性能提升较大。 接着，2015 年又推出了InceptionNet［14］，通过拓宽网络结构取得了较好的效果，提供了CNN 模型构建的另一种思路。 He 等学者［15］提出了ResNet、即深度残差网络，其对残差块的运用十分具有开创性。 本论文所提出的算法就是基于残差块的思想进行搭建的，并对传统的损失函数做了改进，得到了最终的网络框架。

3.2 神经网络框架

本文提出的神经网络架构如图6 所示。 由图6可看到，网络所用到的卷积核都是3×3 的卷积核，因为较小的卷积核可以有效减少参数，并且通过小尺寸的卷积核的堆叠可以达到和大尺寸卷积核相同的感受野。 网络结构中最主要的结构是下采样结构和跳连结构，跳连结构和下采样结构的区别在于经过跳连结构的特征在输入和输出尺寸上不会发生变化，而经过下采样的结构输出相当于输入的一半，跳连结构的作用是用来加深网络的有效深度，下采样结构是防止网络在提取图片特征时丢失图片细节。该网络结构接受要检测的图片，首先经过一个3×3的卷积提取特征，再经过一个最大池化层扩大感受野去除冗余信息，然后再经过跳连结构和下采样结构进行图片特征细节提取，最后经过平均池化层和全连接层得到最终的检测结果输出。 该网络架构对提取图片细节有较好的效果，可以有效处理所遇到的缺陷问题。

图6 神经网络架构图Fig. 6 Architecture diagram of neural network

3.3 损失函数改进

传统损失函数的数学定义公式为：

其中，yi，j为预期输出值；y′i，j为深度学习模型预测值；f为softmax激活函数；c为类别疵病数；N为一个批量的数据量。

该损失函数有2 个缺点。 数据集中每种样本缺陷的数量是不一样的，所以如果按照上面的损失函数进行训练就会导致样本数多的那个疵病类别预测率较高而对于样本数较少的疵病类别预测效果特别差，这是错误的。 另一个传统损失函数对于难预测的样本和易预测样本对于损失函数的贡献是一样的，难预测样本和易预测样本定义，对于某个疵病样本预测值为0.7 的、较样本预测值为0.6 来说为相对易预测样本，而网络应该是对于难预测的样本给予更多的注意力。 改进的损失函数见下式：

与传统的损失函数相比，改进后的损失函数多了2 个超参数、即α，β，MX是某类缺陷参与训练的样本累加数，当某类缺陷样本数，参与损失函数训练越多，α越小，代表其在损失函数中权重越小，就可以解决传统损失函数中的第一个问题。 当预测值越靠近1 时，该样本就是越容易区分的样本，β值越小，在损失函数中的权重也就越小，就可以解决传统损失函数的第二个问题。

4 实验结果对比

把收集到的缺陷图片，利用文章所提到的传统图像处理方法进行图像预处理，再按照前文所提到的划分数据集的策略，把图像划分为训练集和验证集，把划分好的训练集输入到利用深度学习搭建的网络结构中训练。 在该网络中，本文改进了网络结构和损失函数，每20 轮利用验证集进行验证，训练过程中准确率的变换情况如图7 所示，在训练200 轮后网络收敛，在验证集上的准确率达到了92.41%的准确率。

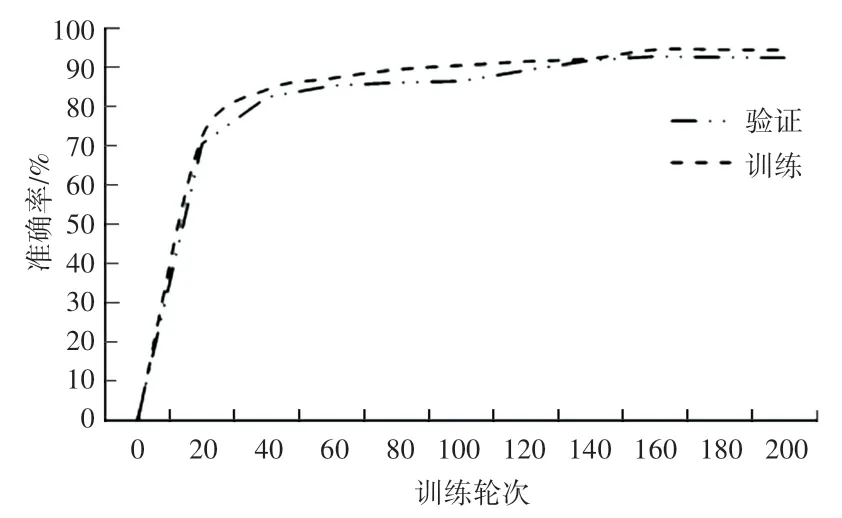
图7 网络训练准确率Fig. 7 Accuracy of network training

网络基本参数的设定见表1。 由表1 可知，实验选用的是Adam 优化器，学习率设定的为0.1，批次大小设定为32，训练轮次设定为200 轮。 把相同的数据集、连同网络基本参数设定为表1 中的基本参数，比较各个网络的性能，性能对比见表2。 由表2 可以看到，文中所提算法在该数据集上的准确率最高，在检测时间上也在可以接受的范围之内，该网络性能可以满足FPCB 的检测要求。

表1 网络基本参数设定Tab. 1 Configuration of basic network parameters

表2 网络性能对比Tab. 2 Comparison of network performance

5 结束语

随着电子工业的快速发展，FPCB 的应用也越来越多，为确保FPCB 生产的合格率，针对目前自动化检测的需要，设计开发了一套缺陷检测算法，该算法把传统图像处理技术与深度学习方法进行了结合来对FPCB 进行缺陷检测。 由于本文提出的缺陷检测算法可替代传统人工判定缺陷，极大地提高了检测的准确度和速度，该工作对FPCB 的生产制造有着重大的意义。