HSMOTE－AdaBoost： 改进混合边界重采样集成分类算法

李 静， 刘 姜， 倪 枫， 李笑语

（上海理工大学管理学院， 上海 200093）

0 引 言

在实际生活中，大部分的数据集都是不平衡的，即某些类会比其他类具有更多的实例，在这种情况下少数类的信息得不到充分的利用［1］。 类不平衡问题给标准的分类学习算法带来了巨大的挑战，在不平衡的数据集上，大多数分类器倾向于对少数实例进行错误分类，而不是对多数实例进行错误分类［2－4］。 但在现实生活中，少数类的错分代价会远高于多数类。 类不平衡问题普遍存在于许多领域，如网络入侵检测［5］、情感分析［6－7］、欺诈检测［8－9］、医疗疾病诊断检测［10］和故障诊断［11］等领域。 大多数标准分类算法往往表现出对多数类的偏倚，因此类的不平衡性往往会损害标准分类器的性能，尤其是对少数类的分类性能［12－13］。

目前，对于不平衡数据集分类问题的解决方案可以分为：数据级、算法级和集成层面［14－15］。 其中，数据级解决方案包括许多不同形式的重采样技术，如随机过采样（ROS）和随机欠采样（RUS）［16－17］。其中，具有代表性的有Chawla 等学者［18］提出了一新型过采样方法，SMOTE 在少数类样本与其k 近邻的连线上随机生成新的样本。 He 等学者［19］开发了一种自适应合成采样（ADASYN），使用密度分布来计算出每个少数样本需要合成的新样本数量。 此外，还有几种混合的采样技术，其中一些方法就是将过采样与数据清理技术相结合，以减少过采样方法引入的重叠。 典型的例子是SMOTE－Tomek［20］和SMOTE－ENN［21］。 这些数据级方法虽然简单易用，但采样方法难以修改数据的分布和偏好相关联，一方面，欠采样会使数据集中一些有价值的数据信息未能得到利用；另一方面，过采样会生成多余数据，尤其是产生噪声数据。 算法级的解决方案旨在开发新的算法或修改现有的算法，加强对少数类分类算法的学习。 研究中，最受欢迎的分支是代价敏感学习，例如，Ting［22］提出了一种实例加权方法来裁剪代价敏感树以提高不平衡数据集的分类效果。Zhang 等学者［23］通过对目标函数中的多数类和少数类设置不同的代价，提出了一种代价敏感神经网络算法，使得少数类样本尽可能地被识别。 其他基于原有算法的改进方案通常是对现有分类算法的改进，文献［24－26］通过引入权重参数来调整分类决策函数，使其向少数类样本偏倚。 然而算法的应用具有特定的情形，大多数的分类模型一旦被确定，则不会动态地调整相应的模型结构及其参数，使得这些算法级改进方法无法动态地学习新增的样本。

集成层面解决方案就是将多个弱分类模型通过一定方式进行组合，得到一个新的、泛化性能更好的强分类器。 Freund 等学者［27］提出的自适应增强（Adaptive Boosting，AdaBoost）算法是Boosting 族中的代表算法。 与其他分类器相比，AdaBoost 能够有效地避免过拟合。 文献［28－29］分别将AdaBoost 与过采样和欠采样结合， 提出 SMOTEBoost 和RUSBoost 算法。 SMOTEBoost 运用SMOTE 进行少数类样本的合成，经过多次迭代得到最终的强分类器。 但SMOTEBoost 算法在训练过程中生成的噪声数据会对分类性能产生影响。 RUSBoost 则采用欠采样方法，先随机删除一些多数类样本，随后使用删除后的数据构造弱分类器。 文献［30］提出一种新的学习算法PCBoost，该算法考虑了属性特征，对少数类进行随机过采样，接着使用信息增益率来构造弱分类器，训练中错误分类的样本会被删除。

上述研究中，虽然有不少基于采样方法与AdaBoost 进行结合，但在采样方法上还需做进一步探讨。 由于集成学习在分类性能上的优越性以及过采样方法使用的普遍性，本文重点关注采样方法与集成学习结合构建分类器。 现有的过采样方法容易引入影响分类性能的噪声样本，而欠采样则会丢失有用的多数类样本的特征信息，尤其是位于分类边界的多数类样本。

针对以上数据级改进方案中采样方法存在易受噪声影响和丢失多数类样本特征信息的问题，本文考虑了多数类样本的类内差异，并保留边界多数类样本；对少数类和多数类采取融合SMOTE 过采样和RUS 欠采样的混合采样策略，并结合集成技术AdaBoost，提出了HSMOTE－AdaBoost 算法。 首先，针对少数类样本中数据缺少和噪声干扰的问题，引入经典的SMOTE 采样算法和K 近邻噪声清除算法。 其次，由于现有的大多数算法尚未考虑到多数类样本之间的类内差异，本文基于平均欧式距离识别并保留边界多数类样本，再对剩下的样本进行随机欠采样。 最后， 运用以J48 为基分类器的AdaBoost 算法进行分类。 结果表明，本文所提出的HSMOTE－AdaBoost 算法与传统的SMOTE－Boost，RUS－ Boost， PC － Boost 算法及改进后的算法KSMOTE－AdaBoost［31］相比，具有更好的分类效果。

1 理论基础

1.1 SMOTE 算法

Chawla 等学者［18］于2002 年提出了少数类样本合成技术，即SMOTE。 该算法的流程步骤如下：

原始训练样本为Tra，少数类样本是P，多数类样本是NP＝ ｛p1，p2，…，ppnum｝，N＝ ｛n1，n2，…，nnmum｝，这里pnum，nmum分别表示少数类样本个数和多数类样本个数。

（1）计算少数类中的每个样本点pi与所有的少数类样本P的欧式距离，得到样本点的k 近邻。

（2）依据样本的采样倍率U， 在k 近邻之间进行线性插值。

（3）合成新的少数类样本：

其中，dj是少数类样本点与其近邻的距离；rj是介于0 到1 之间的随机数。

（4）新合成的少数类样本与原始训练样本Tra进行合并，得到新的训练样本。

1.2 AdaBoost 算法

AdaBoost 算法是经典的Boosting 算法，通过迭代的方式不断提高被误判样本的权值，从而进行样本权值的更新，分类器在下一次分类会把重心放在那些被误分的样本上，以此来达到正确分类所有样本的目的。 算法的训练过程如下：

输入Tra＝｛（X1，Y1），（X2，Y2），…，（Xn，Yn）｝为训练数据集，Xi表示样本实例，Yi为类标签集合，Yi∈｛＋1，－1｝，i＝ 1，2，…，n；迭代循环次数为M

输出最终分类器G（X）

2： form＝1 toM：

2.1： 使用具有权值分布Dm的训练数据集进行学习，得到基本分类器Gm（X）

2.2： 算出Gm（X） 在训练数据集上的分类误差率：

这里，I为指示函数：

2.3：计算Gm（X） 的系数：

2.4：更新训练数据集的权值分布：

其中，Zm为规范化因子，计算公式为：

3： 构建基本分类器的线性组合：

4： 得到最终的分类器：

2 HSMOTE－AdaBoost 算法

针对不平衡数据的二分类问题，过采样会增加多余数据引入噪声样本，而欠采样会丢失一些有用信息，这2 个问题极大地影响了算法的分类性能。HSMOTE－AdaBoost 算法考虑了边界多数类样本特征信息的价值，将SMOTE 算法和RUS 算法进行了结合，并针对RUS 算法中存在随机删除边界多数类样本的问题进行了改进。 位于2 个类边界上的实例是该分类样本的必要实例，在确定决策边界时至关重要，将其删除会降低分类器的性能。 因此，本文提出的HSMOTE－AdaBoost 算法考虑了边界多数类样本，并试图保持必要的多数类实例，分类模型图如图1 所示。 首先，使用SMOTE 过采样合成少数类实例，以平衡数据集；接着，删除原始数据中的一些噪声数据，提高合成样本的质量；然后，识别多数类的边界实例，并将其添加到输出数据集中。 同时，对剩余的数据进行随机欠采样。 最后，使用AdaBoost 集成算法生成强分类器，实验结果表明该分类器的性能得到了有效的提升。

图1 分类模型图Fig. 1 Classification model diagram

2.1 算法HSMOTE－AdaBoost 的训练过程

（1）合成少数类样本。 将合成少数类过采样（SMOTE）预处理技术应用到数据集Timbal中，在少数类中引入人工实例，生成数据集T⌒imbal。 具体步骤详述如下。

①原始训练样本是Timbal，少数类样本为P，多数类是N，P＝（p1，p2，…，pn），N＝（n1，n2，…，nm），n，m分别表示少数类样本个数及多数类样本个数。计算少数类样本点pj与少数类P的欧式距离，得到该样本点的k 近邻。

②依据采样倍率U在k 近邻中进行线性插值。

③合成新的少数类样本：

其中，di表示少数类样本点与其近邻的距离，ri是介于0 到1 之间的随机数。

④新合成的少数类样本和原始训练样本进行合并，从而得到新的训练样本T⌒imbal。

（2）识别和删除噪声。 若少数类样本点在k 近邻中有k′个多数类样本，显然0 ≤k′ ≤k，若k′ ≤，则为噪声。

（3）识别多数类的边界样本Nborder，并将其放入输出数据集Tbal中。 具体步骤分述如下。

①算出各多数类样本点ni（i＝1，2，……，m）到少数类样本点pj（j＝1，2，…，n） 的距离之和为

②求平均距离：

③当多数类样本ni满足时，将其划分到Tbal中。

（4）对数据集E应用随机欠采样，将随机选取的样本推送到输出数据集Tbal，并推得：

（5）将处理后的平衡数据集作为模型的输入，使用AdaBoost 集成技术得到最终的分类结果。

2.2 算法HSMOTE－AdaBoost 的详细步骤

输入D为数据集，K为过采样算法中选择的最近邻个数，M为迭代的次数

输出集成分类器

1： 将数据集D分成10 份，其中2 份为测试集TestData，剩下即训练集TrainData

2： 运用SMOTE 过采样算法生成新的少数类样本

3： 用k 近邻算法得到少数类样本的最近邻集合，依据判别条件对噪声样本进行识别及删除。 判别条件为：若少数类样本中k 近邻超过2／3 的样本是多数类，则为噪声样本

4： 基于所有多数类样本点对各个少数类样本点的平均欧式距离识别边界多数类样本，并将其单独放在NewTrainData中。 识别条件为：若该多数类样本点到所有少数类样本点的欧式距离之和小于平均距离，则该样本点为边界多数类样本点

5： 对剩余的数据进行随机欠抽样得到NewTrainData

6： 赋予NewTrainData中每个实例相同的权重。

7： form＝1 toM

8： 根据实例的权值有放回地抽样得到Dm

9： 由Dm得到基分类器Gm（X）

10： 使用Gm（X） 对NewTrainData中的实例进行分类，根据式（12）计算Gm（X） 的错误率em：

其中，wm，i表示第m轮中第i个实例Xi的权值；Gm（Xi） ≠Yi表示实例Xi被错分；Yi为类标签。

11： ifem ＞0.5 then 转步骤7

12： end if

13： for 对正确分类的每个实例执行如下步骤：

15： 归一化所有实例的权值

16： end for

17： 将每个类的权值赋予0，对TestData的所有实例执行以下步骤

18： fori＝1 toM：

19： 根据式（13）计算Gi（X） 对测试集中实例Xi的权值Wi：

20： 将Wi加到Gi（X） 所预测的类上，若Xi被正确分类，则其值为0，否则为1。

21： end for

22： 返回权值最大的类，即为Xi的类别

23： end for

3 仿真实验

3.1 实验数据集

实验使用来自KEEL 公开数据集的6 组数据集，考虑了数据集的样本数、特征数及不平衡率。 实验之前对数据集进行预处理，将训练集和测试集归一化到［0，1］区间，表1 展示了实验数据集的基本信息。

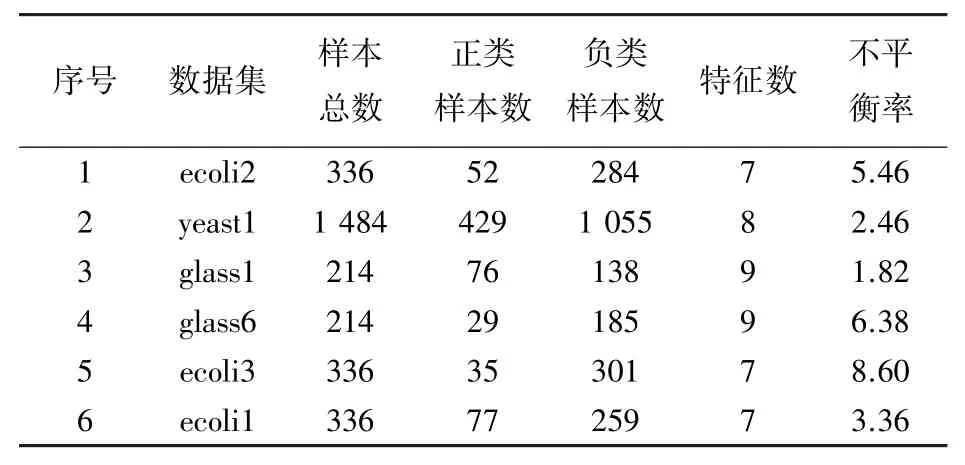
表1 实验数据集Tab. 1 Experimental dataset

3.2 性能评价指标

在对数据集进行二分类时，不能简单地采用整体精确度的高低来评价分类器性能的优劣。 因为即使分类器对少数类样本的识别完全错误，总体的精确度也会比较高，所以仅靠这个单一评价指标并没有参考价值。 为了全面体现分类性能，本文采用了综合评价指标F － measure，G － mean和AUC，F －measure，G － mean和AUC取值均在0 到1 之间，且值越大，说明分类器的分类性能越好。 在介绍这些指标前，先引入混淆矩阵。 混淆矩阵［32］可以将预测分类结果和实际分类结果以矩阵的形式直观地表示出来。 混淆矩阵见表2。

表2 混淆矩阵Tab. 2 Confusion matrix

根据表2 可得到以下评价指标。

（1）召回率（Recall）。 指真少数类占所有少数类的比例。 可由如下公式来求值：

（2） 精确率（Precision）。 指真少数类占所有被预测为少数类的比例。 可由如下公式来求值：

（3）F － measure［33］，又称F － Score，兼顾精确度和召回率。 可由如下公式来求值：

其中，α是取值为1 的比例系数。

（4）G － mean［34］。 是一种有效衡量不平衡数据分类方法的指标，只有正类、负类两者召回率都高时，G － mean值才会高，表明分类器的分类性能较优。 可由如下公式来求值：

（5）AUC［35］。ROC曲线以假正率（FPrate）和真正率（TPrate） 为轴，以可视化的方式展现正确分类的收益和误分类的代价之间的关联。ROC曲线下方的面积称为AUC（Area Under Curve），AUC可以量化分类器的预测性能，AUC的取值范围为0 到1，AUC值越高，模型的预测性能越好。

3.3 实验设置

为了验证本文所提出的算法的优越性，将本文算法与传统的SMOTE－Boost，RUS－Boost，PC－Boost及改进后的KSMOTE－AdaBoost 算法进行了比较。本文使用Python 语言，Spyder 开发环境对各种算法进行仿真实验。 与以往文献［36］一致，SMOTE 算法的k 近邻数设为5 时所合成的少数类样本质量较高。 实验选用J48 决策树作为基分类器，调用Weka软件中的C4.5 函数包实现J48 分类器。 实验中将数据集的20%作为测试集，80%作为训练集，采用10 次五折交叉验证的平均值作为最终的评价结果。

3.4 实验结果分析

图2～图4 及表3～表5 列出了使用本文算法和其他4 种不同采样方法与集成学习技术结合算法在6个不同数据集上的F － measure、G － mean值及AUC的比较结果和具体数值，其中加粗部分为在该数据集上的最优结果。 从图2～图4 可以看出，由本文算法所得到的F － measure、G － mean及AUC值总体上优于其他4 种对比算法。 从表3～表5 可以得出本文的分类模型在F － measure、G － mean及AUC值上均得到了提升，尤其是对比RUS－Boost 算法。 在数据集ecoli2、yeast1、glass6、ecoli3 上，其分类评估指标均优于其他对比算法，F－measure的提升值高达22.97%，G － mean的提升值为13.88%，AUC的最高提升值为10.03%。 从表3 的F － measure值可看出，HSMOTEAdaBoost 算法除了在数据集ecoli1 略低于SMOTEBoost 之外，在其他5 个数据集上均有最佳表现。 从表4～表5 得出，在数据集glass1 上，G － mean值稍逊于KSMOTE－AdaBoost 算法，AUC指标略小于SMOTE－Boost 算法，但其F － measure的提升值为3.99%。原因在于其不平衡比率较小，边界样本的重要性未得到充分体现。 虽然在部分数据集中的AUC值与其他4 种算法相差不大，但是随着不平衡率的提升，性能提升百分比在不断增大，在不平衡比率最大的数据集ecoli3 上，相对于其他4 种算法，性能提升了10.03%。 此外，在部分数据集、如yeast1，ecoli2 中，使用HSMOTE－AdaBoost 算法优于RUS－Boost 算法，这是因为在使用随机欠采样后有可能会删除一些潜在、有价值的多数类样本，而本文所提出的算法有效解决了这个问题，尽可能地保留了必要的实例从而提升了分类性能。

表3 不同算法的F－measureTab. 3 F－measure of different algorithms

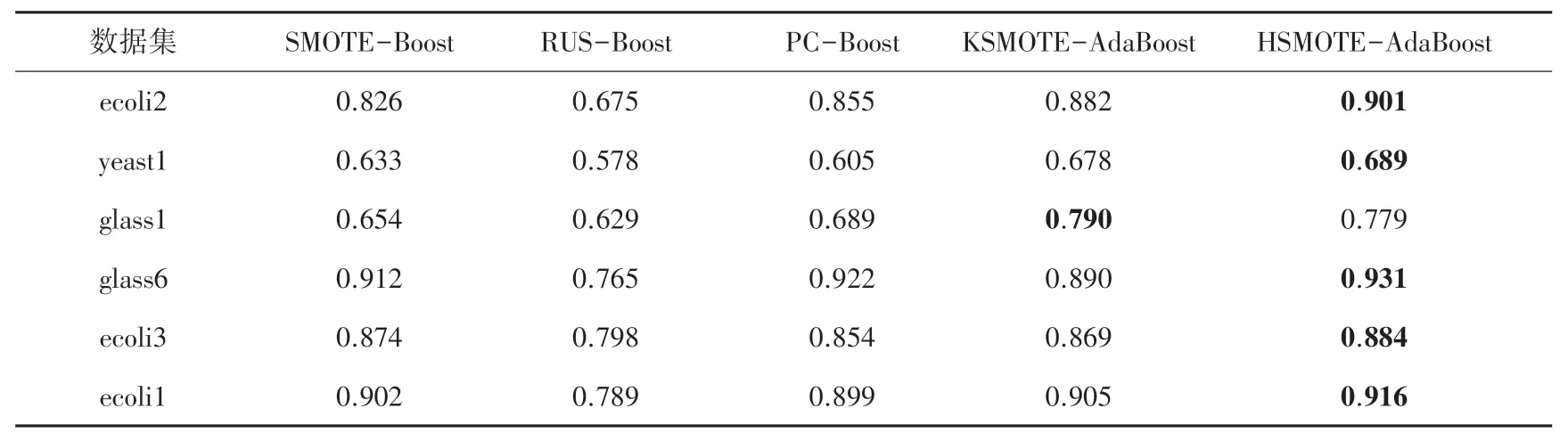
表4 不同算法的G－meanTab. 4 G－mean of different algorithms

表5 不同算法的AUCTab. 5 AUC of different algorithms

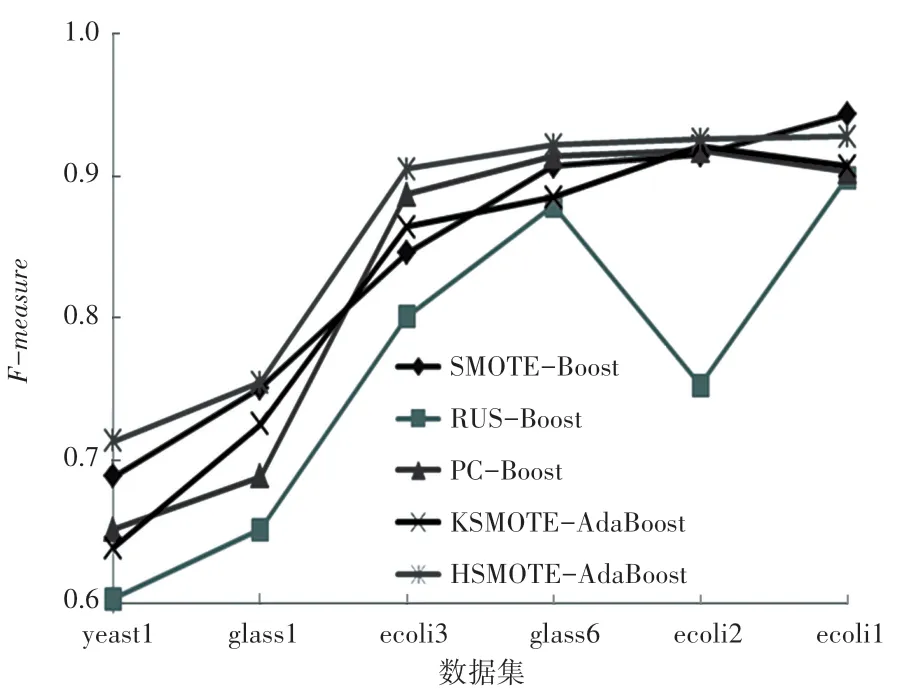
图2 不同算法的F－measure 对比图Fig. 2 F－measure comparison of different algorithms

图3 不同算法的G－mean 对比图Fig. 3 G－mean comparison of different algorithms

图4 不同算法的AUC 对比图Fig. 4 AUC comparison of different algorithms

4 结束语

针对二分类问题中不平衡数据集造成分类器分类性能低下的问题，本文考虑了多数类样本的类内差异，并保留了必要的边界多数类样本，将SMOTE过采样与随机欠采样组合运用及改进，并与AdaBoost 相结合提出了一种解决类不平衡问题的HSMOTE－AdaBoost 算法。 与传统的SMOTE－Boost、RUS－Boost、PC－Boost 及改进后的算法KSMOTEAdaBoost 相比，实验表明该算法训练的分类器能有效地处理类不平衡问题，分类性能更优。

此外，本文的改进算法也存在进一步研究的价值，接下来可以结合其他经典的集成算法研究其分类性能。 其次，从实验结果可以发现，在类不平衡比率越大的数据集上的分类效果越好，亟需从理论上对该结果做进一步的探讨和验证。 最后，本文所提出的算法对二分类问题的分类性能提升比较明显，然而在现实生活中的大多数数据都是多类别的，未来将着重研究如何提高多类别分类问题的分类性能。